小波神经网络(WNN)的实现(Python,附源码及数据集)
文章目录
- 一、理论基础
- 1、小波神经网络结构
- 2、前向传播过程
- 3、反向传播过程
- 4、建模步骤
- 二、小波神经网络的实现
- 1、训练过程(WNN.py)
- 2、测试过程(test.py)
- 3、测试结果
- 4、参考源码及实验数据集
一、理论基础
小波神经网络(Wavelet Neural Network,简称WNN)是基于小波变换理论构造而成,其原理原理与反向传播神经网络(BPNN)较为接近,最主要的特征是它的隐含层神经元激活函数为小波基函数,这一特性使其充分利用了小波变换的局部化性质和神经网络的大规模数据并行处理、自学习能力,因而具有较强的逼近能力和较快的收敛速度。
反向传播神经网络(BPNN)原理参考:
反向传播神经网络(BPNN)的实现(Python,附源码及数据集)
1、小波神经网络结构
小波神经网络的结构图如下图所示:
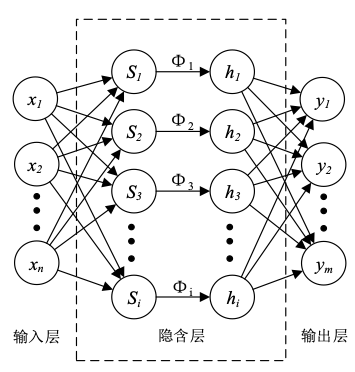
2、前向传播过程
假设输入层、隐含层、输出层的节点数分别为n、i和m,则数据由输出层传递到隐含层时,隐含层第j个节点的输入数据的计算公式如下:

其中x_k为输入数据中第k个样本数据,ω_kj为隐含层节点的连接权值。
上述计算结果在隐含层节点处进行小波基的伸缩变化,具体的变换公式如下:
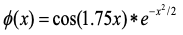
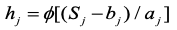
其中∅(x)为小波基函数,b_j为基函数的平滑因子,a_j为基函数的伸缩因子,h_j为隐含层第j个节点的输出数据。
最后隐含层第j个节点的输出数据进入输出层,经过计算后从输出层的t个节点输出,此节点上的计算公式如下:

其中ω_jt为输出层的连接权值,φ为激活函数。
激活函数原理参考:
神经网络基础知识之激活函数
3、反向传播过程
由前向传播过程可以了解到,数据在神经元与神经元之间的传递是单向的,每个神经元只接受上一层神经元传递过来的数据并对其处理。在这个处理过程中,小波神经网络主要有四个参数参与计算,这四个参数分别是小波基函数的平滑因子b_j与伸缩因子a_j以及隐含层与输出层的两个连接权值,这四个参数值的大小将直接影响网络的性能。因此WNN的训练过程如BPNN一样主要使用反向传播算法如随机梯度下降法(SGD)对这四个参数进行不断的修正。
以输出层的权值为例,其更新公式如下:

其中E为误差函数,μ为学习率。
损失函数原理参考:
机器学习基础知识之损失函数
反向传播原理参考:
神经网络之反向传播算法(梯度、误差反向传播算法BP)
4、建模步骤
以使用小波神经网络进行预测为例,可以将小波神经网络预测模型的建模步骤总结如下:
- 根据输入数据的相关特征确定小波神经网络输入层、隐含层以及输出层的节点数;
- 选择一种参数初始化方法对小波神经网络隐含层的连接权值、平滑因子和伸缩因子、输出层的连接权值进行随机初始化;
- 数据由输入层输入小波神经网络,传递至隐含层后经小波变换对数据进行非线性转换;
- 数据在隐含层输出后传递至输出层,在与输出层的连接权值进行线性计算后由激活函数进行非线性转换,最后得到网络的前向传播输出;
- 选择一种损失函数对网络的前向传播输出以及目标值进行相关计算得到损失值;
- 以输出层的损失值计算得到输出层连接权值以及阈值的梯度,选择一种反向传播算法对它们进行调整;
- 损失值传递至隐含层,同样使用相同的反向传播算法对隐含层的中心点以及宽度向量进行调整;
- 获得一个参数得到更新后的小波神经网络;
- 在达到最大迭代次数或满足停止迭代条件之前,重复步骤4到步骤8,在达到最大迭代次数后,输出所有参数确定的小波神经网络。
参数初始化方法参考:
神经网络基础知识之参数初始化
二、小波神经网络的实现
以数据预测为例,下面介绍基于Python实现小波神经网络的过程。
选用某省市的表层土壤重金属元素数据集作为实验数据,该数据集总共96组,随机选择其中的24组作为测试数据集,72组作为训练数据集。选取重金属Ti的含量作为待预测的输出特征,选取重金属Co、Cr、Mg、Pb作为模型的输入特征。
1、训练过程(WNN.py)
#库的导入
import numpy as np
import pandas as pd
import math#激活函数
def tanh(x):return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
#激活函数偏导数
def de_tanh(x):return (1-x**2)
#小波基函数
def wavelet(x):return (math.cos(1.75*x)) * (np.exp((x**2)/(-2)))
#小波基函数偏导数
def de_wavelet(x):y = (-1) * (1.75 * math.sin(1.75 * x) + x * math.cos(1.75 * x)) * (np.exp(( x **2)/(-2)))return y#参数设置
samnum = 72 #输入数据数量
hiddenunitnum = 8 #隐含层节点数
indim = 4 #输入层节点数
outdim = 1 #输出层节点数
maxepochs = 500 #迭代次数
errorfinal = 0.65*10**(-3) #停止迭代训练条件
learnrate = 0.001 #学习率#输入数据的导入
df = pd.read_csv("train.csv")
df.columns = ["Co", "Cr", "Mg", "Pb", "Ti"]
Co = df["Co"]
Co = np.array(Co)
Cr = df["Cr"]
Cr = np.array(Cr)
Mg=df["Mg"]
Mg=np.array(Mg)
Pb = df["Pb"]
Pb =np.array(Pb)
Ti = df["Ti"]
Ti = np.array(Ti)
samplein = np.mat([Co,Cr,Mg,Pb])
#数据归一化,将输入数据压缩至0到1之间,便于计算,后续通过反归一化恢复原始值
sampleinminmax = np.array([samplein.min(axis=1).T.tolist()[0],samplein.max(axis=1).T.tolist()[0]]).transpose()#对应最大值最小值
#待预测数据为Ti
sampleout = np.mat([Ti])
sampleoutminmax = np.array([sampleout.min(axis=1).T.tolist()[0],sampleout.max(axis=1).T.tolist()[0]]).transpose()#对应最大值最小值
sampleinnorm = ((np.array(samplein.T)-sampleinminmax.transpose()[0])/(sampleinminmax.transpose()[1]-sampleinminmax.transpose()[0])).transpose()
sampleoutnorm = ((np.array(sampleout.T)-sampleoutminmax.transpose()[0])/(sampleoutminmax.transpose()[1]-sampleoutminmax.transpose()[0])).transpose()#给归一化后的数据添加噪声
noise = 0.03*np.random.rand(sampleoutnorm.shape[0],sampleoutnorm.shape[1])
sampleoutnorm += noise#
scale = np.sqrt(3/((indim+outdim)*0.5))
w1 = np.random.uniform(low=-scale,high=scale,size=[hiddenunitnum,indim])
b = np.random.uniform(low=-scale, high=scale, size=[hiddenunitnum,1])
a = np.random.uniform(low=-scale, high=scale, size=[hiddenunitnum,1])
w2 = np.random.uniform(low=-scale,high=scale,size=[hiddenunitnum,outdim])#对隐含层的连接权值w1、平滑因子被b和伸缩因子a、输出层的连接权值w2进行随机初始化
inputin=np.mat(sampleinnorm.T)
w1=np.mat(w1)
b=np.mat(b)
a=np.mat(a)
w2=np.mat(w2)#errhistory存储每次迭代训练计算的误差
errhistory = np.mat(np.zeros((1,maxepochs)))
#开始训练
for i in range(maxepochs):#前向计算:#hidden_out为隐含层输出hidden_out = np.mat(np.zeros((samnum,hiddenunitnum)))for m in range(samnum):for j in range(hiddenunitnum):d=((inputin[m, :] * w1[j, :].T) - b[j,:]) * (a[j,:] ** (-1))hidden_out[m,j] = wavelet(d)#output为输出层输出output = tanh(hidden_out * w2)#计算误差out_real = np.mat(sampleoutnorm.transpose())err = out_real - outputloss = np.sum(np.square(err))#判断是否停止训练if loss < errorfinal:breakerrhistory[:,i] = loss#反向计算out_put=np.array(output.T)belta=de_tanh(out_put).transpose()#分别计算每个参数的误差项for j in range(hiddenunitnum):sum1 = 0.0sum2 = 0.0sum3 = 0.0sum4 = 0.0sum5 = 0.0for m in range(samnum):sum1+= err[m,:] * belta[m,:] * w2[j,:] * de_wavelet(hidden_out[m,j]) * (inputin[m,:] / a[j,:])#1*1sum2+= err[m,:] * belta[m,:] * w2[j,:] * de_wavelet(hidden_out[m,j]) * (-1) * (1 / a[j,:])#1*1sum3+= err[m,:] * belta[m,:] * w2[j,:] * de_wavelet(hidden_out[m,j]) * (-1) * ((inputin[m,:] * w1[j,:].T - b[j,:]) / (a[j,:] * a[j,:]))#1*1sum4+= err[m,:] * belta[m,:] * hidden_out[m,j]delta_w1 = sum1delta_b = sum2delta_a = sum3delta_w2 = sum4#根据误差项对四个参数进行更新w1[j,:] = w1[j,:] + learnrate * delta_w1b[j,:] = b[j,:] + learnrate * delta_ba[j,:] = a[j,:] + learnrate * delta_aw2[j,:] = w2[j,:] + learnrate * delta_w2print("the generation is:",i+1,",the loss is:",loss)print('更新的w1:',w1)
print('更新的b:',b)
print('更新的w2:',w2)
print('更新的a:',a)
print("The loss after iteration is :",loss)np.save("w1.npy",w1)
np.save("b.npy",b)
np.save("w2.npy",w2)
np.save("a.npy",a)
2、测试过程(test.py)
#库的导入
import numpy as np
import pandas as pd
import math#小波基函数
def wavelet(x):return (math.cos(1.75*x)) * (np.exp((x**2)/(-2)))
#激活函数tanh
def tanh(x):return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))#输入数据的导入,用于测试数据的归一化与返归一化
df = pd.read_csv("train.csv")
df.columns = ["Co", "Cr", "Mg", "Pb", "Ti"]
Co = df["Co"]
Co = np.array(Co)
Cr = df["Cr"]
Cr = np.array(Cr)
Mg=df["Mg"]
Mg=np.array(Mg)
Pb = df["Pb"]
Pb =np.array(Pb)
Ti = df["Ti"]
Ti = np.array(Ti)
samplein = np.mat([Co,Cr,Mg,Pb])
sampleinminmax = np.array([samplein.min(axis=1).T.tolist()[0],samplein.max(axis=1).T.tolist()[0]]).transpose()#对应最大值最小值
sampleout = np.mat([Ti])
sampleoutminmax = np.array([sampleout.min(axis=1).T.tolist()[0],sampleout.max(axis=1).T.tolist()[0]]).transpose()#对应最大值最小值#导入WNN.py训练好的参数
w1=np.load('w1.npy')
b=np.load('b.npy')
a=np.load('a.npy')
w2=np.load('w2.npy')
w1 = np.mat(w1)
w2 = np.mat(w2)
b = np.mat(b)
a = np.mat(a)#隐含层节点数
hiddenunitnum = 8
#测试数据数量
testnum = 24#测试数据的导入
df = pd.read_csv("test.csv")
df.columns = ["Co", "Cr", "Mg", "Pb", "Ti"]
Co = df["Co"]
Co = np.array(Co)
Cr = df["Cr"]
Cr = np.array(Cr)
Mg=df["Mg"]
Mg=np.array(Mg)
Pb = df["Pb"]
Pb =np.array(Pb)
Ti = df["Ti"]
Ti = np.array(Ti)
input=np.mat([Co,Cr,Mg,Pb])#测试数据中输入数据的归一化
inputnorm=(np.array(input.T)-sampleinminmax.transpose()[0])/(sampleinminmax.transpose()[1]-sampleinminmax.transpose()[0])
#hidden_out2用于保存隐含层输出
hidden_out = np.mat(np.zeros((testnum,hiddenunitnum)))
#计算隐含层输出
for m in range(testnum):for j in range(hiddenunitnum):d = ((inputnorm[m, :] * w1[j, :].T) - b[j, :]) * (a[j, :] ** (-1))hidden_out[m, j] = wavelet(d)
#计算输出层输出
output = tanh(hidden_out * w2 )
#对输出结果进行反归一化
diff = sampleoutminmax[:,1]-sampleoutminmax[:,0]
networkout2 = output*diff+sampleoutminmax[0][0]
networkout2 = np.array(networkout2).transpose()
output1=networkout2.flatten()#降成一维数组
output1=output1.tolist()
for i in range(testnum):output1[i] = float('%.2f'%output1[i])
print("the prediction is:",output1)#将输出结果与真实值进行对比,计算误差
output=Ti
rmse = (np.sum(np.square(output-output1))/len(output)) ** 0.5
mae = np.sum(np.abs(output-output1))/len(output)
average_loss1=np.sum(np.abs((output-output1)/output))/len(output)
mape="%.2f%%"%(average_loss1*100)
f1 = 0
for m in range(testnum):f1 = f1 + np.abs(output[m]-output1[m])/((np.abs(output[m])+np.abs(output1[m]))/2)
f2 = f1 / testnum
smape="%.2f%%"%(f2*100)
print("the MAE is :",mae)
print("the RMSE is :",rmse)
print("the MAPE is :",mape)
print("the SMAPE is :",smape)#计算预测值与真实值误差与真实值之比的分布
A=0
B=0
C=0
D=0
E=0
for m in range(testnum):y1 = np.abs(output[m]-output1[m])/np.abs(output[m])if y1 <= 0.1:A = A + 1elif y1 > 0.1 and y1 <= 0.2:B = B + 1elif y1 > 0.2 and y1 <= 0.3:C = C + 1elif y1 > 0.3 and y1 <= 0.4:D = D + 1else:E = E + 1
print("Ratio <= 0.1 :",A)
print("0.1< Ratio <= 0.2 :",B)
print("0.2< Ratio <= 0.3 :",C)
print("0.3< Ratio <= 0.4 :",D)
print("Ratio > 0.4 :",E)
3、测试结果
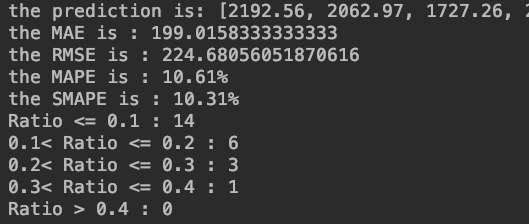
注:由于每次初始化生成的参数不同,因此对参数设置相同的神经网络进行多次训练和预测,测试结果不会完全一致,此外测试结果的好坏也会受到隐含层节点数、学习率、训练次数等参数的影响。
4、参考源码及实验数据集
参考源码及实验数据集
相关文章:

小波神经网络(WNN)的实现(Python,附源码及数据集)
文章目录一、理论基础1、小波神经网络结构2、前向传播过程3、反向传播过程4、建模步骤二、小波神经网络的实现1、训练过程(WNN.py)2、测试过程(test.py)3、测试结果4、参考源码及实验数据集一、理论基础 小波神经网络(…...

商标干货!所有企业都值得收藏!
商标,是用于识别和区分不同商品或服务来源的标志,代表了企业的产品质量和服务保证,可以说,商标承载了一个企业的信誉,是企业参与市场竞争的重要工具,对于企业及其产品的重要性不言而喻。 根据《商标法》四十…...

4次迭代,让我的 Client 优化 100倍!泄漏一个 人人可用的极品方案!
4次迭代,让我的HttpClient提速100倍 在大家的生产项目中,经常需要通过Client组件(HttpClient/OkHttp/JDK Connection)调用第三方接口。 尼恩的一个生产项目也不例外。 在一个高并发的中台生产项目中。有一个比较特殊的请求,一次…...

并查集(高级数据结构)-蓝桥杯
一、并查集并查集(Disioint Set):一种非常精巧而实用的数据结构用于处理不相交集合的合并问题。用于处理不相交集合的合并问题。经典应用:连通子图。最小生成树Kruskal算法。最近公共祖先。二、应用场景有n个人,他们属于不同的帮派。 已知这些…...
你是真的“C”——C语言详解求两个正数最小公倍数的3种境界
C语言详解求两个正数最小公倍数的3种境界~😎前言🙌必备小知识~😘求最小公倍数境界1~ 😊求最小公倍数境界2~ 😊求最小公倍数境界3~ 😊总结撒花💞博客昵称:博客小梦😊 最喜…...

【java】Spring Cloud --Feign Client超时时间配置以及单独给某接口设置超时时间方法
文章目录feign配置(最常用)ribbon配置hystrix配置单独给某接口设置超时时间FeignClient面对服务级有三种超时时间配置feign配置(最常用) feign:sentinel:enabled: trueclient:config:default://全部服务配置connectTimeout: 5000…...

spark代码
RDD Tom,DataBase,80 Tom,Algorithm,50 Tom,DataStructure,60 Jim,DataBase,90 Jim,Algorithm,60 Jim,DataStructure,80 该系总共有多少学生; val lines sc.textFile("file:///usr/local/spark/sparksqldata/Data01.txt") val par lines.map(ro…...
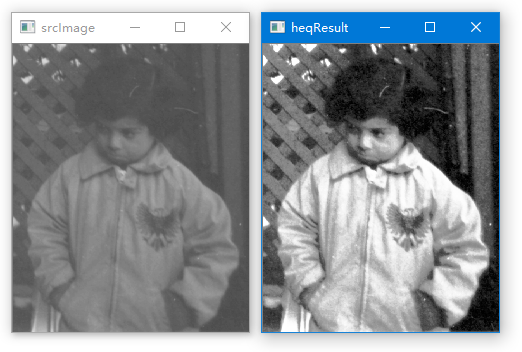
利用OpenCV的函数equalizeHist()对图像作直方图均衡化处理
如果一幅图像的灰度值集中在某个比较窄的区域,则图像的对比度会显得比较小,不便于对图像的分析和处理。 图像的直方图均衡化可以实现将原图像的灰度值范围扩大,这样图像的对比度就得到了提高,从而方便对图像进行后续的分析和处理…...

星河智联Android开发
背景:朋友内推,过了一周约面。本人 2019年毕业 20230208一面 1.自我介绍 2.为啥换工作 3.项目经历(中控面板、智能音箱、语音问的比较细) 4.问题 Handler机制原理?了解同步和异步消息吗?View事件分发…...

【C++】关联式容器——map和set的使用
文章目录一、关联式容器二、键值对三、树形结构的关联式容器1.set2.multiset3.map4.multimap四、题目练习一、关联式容器 序列式容器📕:已经接触过STL中的部分容器,比如:vector、list、deque、forward_list(C11)等,这些容器统称为…...

Promise的实现原理
作用:异步问题同步化解决方案,解决回调地狱、链式操作原理: 状态:pending、fufilled reject构造函数传入一个函数,resolve进入then,reject进入catch静态方法:resolve reject all any react ne…...
【MFC】数据库操作——ODBC(20)
ODBC:开放式数据库连接,是为解决异构数据库(不同数据库采用的数据存储方法不同)共享而产生的。ODBC API相对来说非常复杂,这里介绍MFC的ODBC类。 添加ODBC用户DSN 首先,在计算机中添加用户DSN:(WIN10下&a…...
旺店通与金蝶云星空对接集成采购入库单接口
旺店通旗舰奇门与金蝶云星空对接集成采购入库单查询连通销售退货新增V1(12-采购入库单集成方案-P)数据源系统:旺店通旗舰奇门旺店通是北京掌上先机网络科技有限公司旗下品牌,国内的零售云服务提供商,基于云计算SaaS服务模式,以体系化解决方案…...
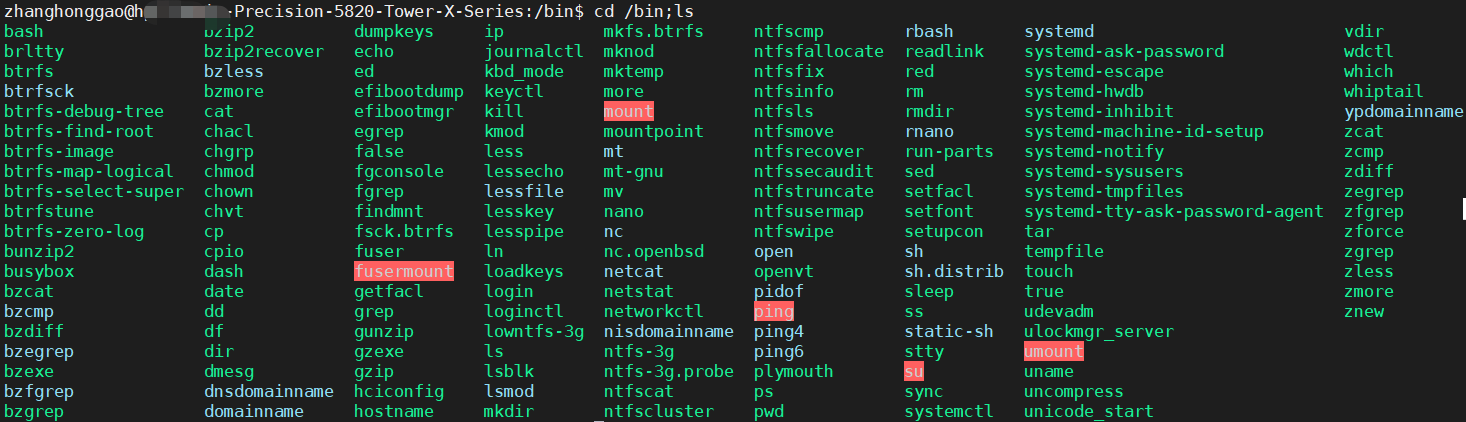
Linux基础-学会使用命令帮助
概述使用 whatis使用 man查看命令程序路径 which总结参考资料概述Linux 命令及其参数繁多,大多数人都是无法记住全部功能和具体参数意思的。在 linux 终端,面对命令不知道怎么用,或不记得命令的拼写及参数时,我们需要求助于系统的…...
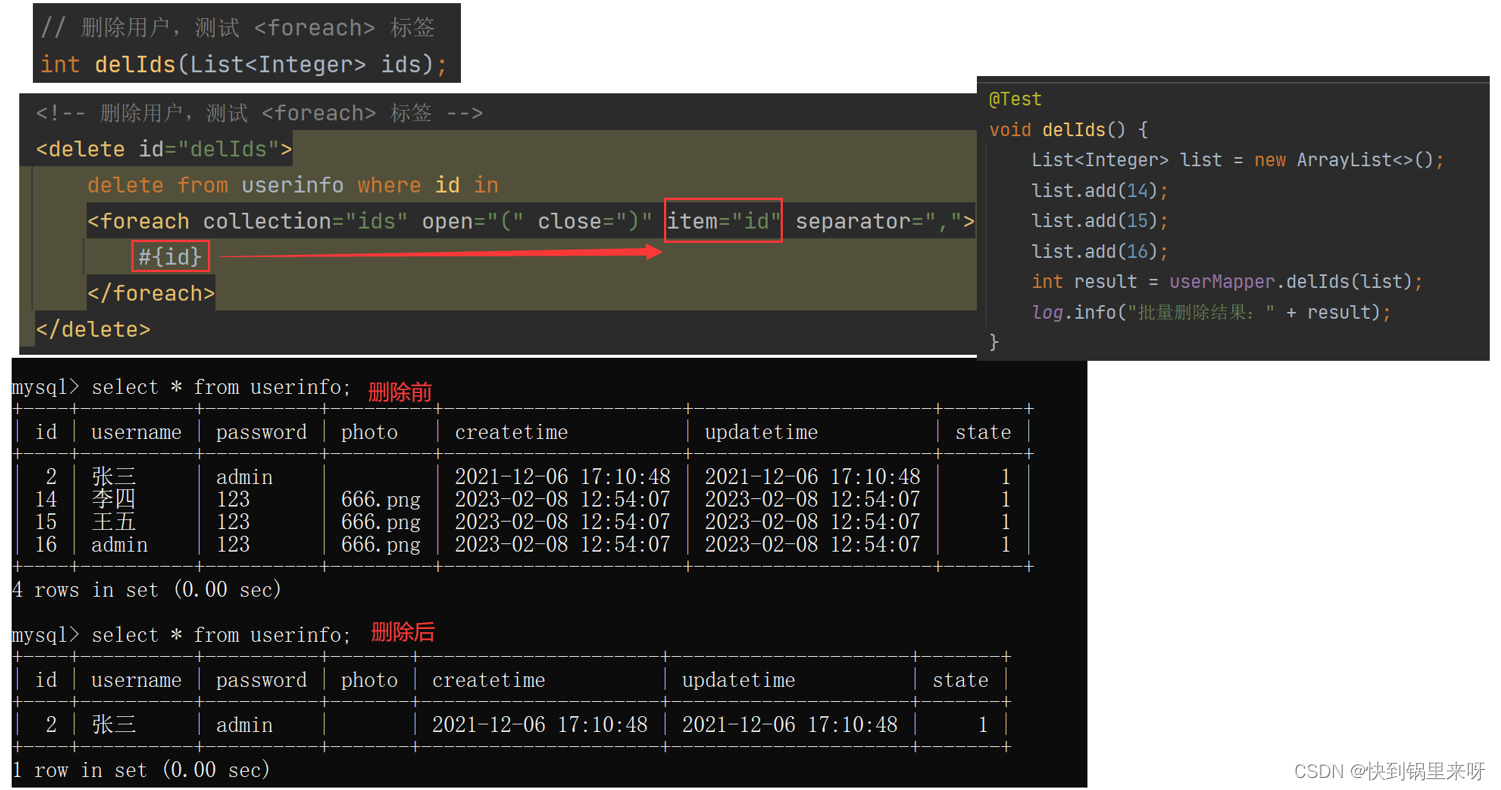
MyBatis 之四(动态SQL之 if、trim、where、set、foreach 标签)
文章目录动态 SQL1. if 标签2. trim 标签3. where 标签4. set 标签5. foreach 标签回顾一下,在上一篇 MyBatis 之三(查询操作 占位符#{} 与 ${}、like查询、resultMap、association、collection)中,学习了针对查询操作的相关知识点…...
 Practice 1006 Sign In and Sign Out)
PAT (Advanced Level) Practice 1006 Sign In and Sign Out
1006 Sign In and Sign Out题目翻译代码分数 25作者 CHEN, Yue单位 浙江大学At the beginning of every day, the first person who signs in the computer room will unlock the door, and the last one who signs out will lock the door. Given the records of signing in’…...

Android入门第64天-MVVM下瀑布流界面的完美实现-使用RecyclerView
前言 网上充满着不完善的基于RecyclerView的瀑布流实现,要么根本是错的、要么就是只知其一不知其二、要么就是一充诉了一堆无用代码、要么用的是古老的MVC设计模式。 一个真正的、用户体验类似于淘宝、抖音的瀑布流怎么实现目前基本为无解。因为本人正好自己空闲时也…...
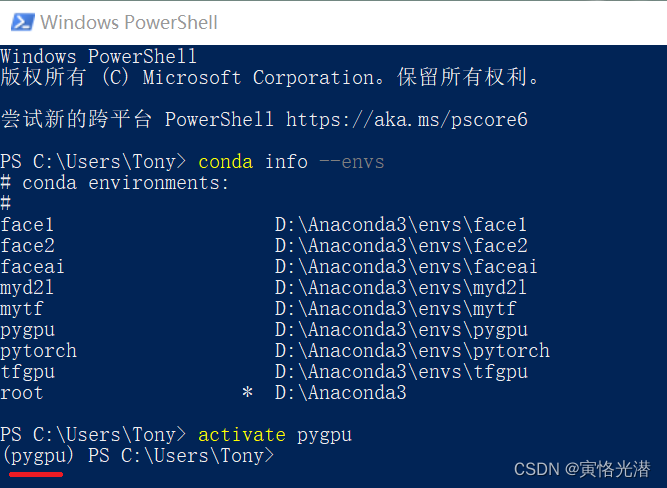
Windows PowerShell中成功进入conda虚拟环境
本人操作系统是Windows10(输入命令cmd或在运运行中输入winver查看)在cmd命令行中大家都很熟悉,很方便进入到指定创建了的虚拟环境中,那么在PowerShell中怎么进入呢?比如在VSCode中的TERMINAL使用的是PowerShell&#x…...

【C++】类与对象理解和学习(中)
专栏放在【C知识总结】,会持续更新,期待支持🌹六大默认成员函数前言每个类中都含有六大默认成员函数,也就是说,即使这个类是个空类,里面什么都没有写,但是编译器依然会自动生成六个默认成员函数…...
大英复习单词和翻译)
每日英语学习(11)大英复习单词和翻译
2023.2.20 单词 1.contemplate 思考、沉思 2.spark 激起 3.venture 冒险 4.stunning 极好的 5.dictate 影响 6.diplomatic 外交的 7.vicious 恶性的 8.premier 首要的 9.endeavor 努力 10.bypass 绕过 11.handicaps 不利因素 12.vulnerable 脆弱的 13.temperament 气质、性格…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
