[Go版]算法通关村第十三关白银——数字数学问题之数组实现加法、幂运算
目录
- 数组实现加法专题
- 题目:数组实现整数加法
- 思路分析:数组末尾开始,逐个元素+1,=10就进位,!=10就退出
- 复杂度:时间复杂度 O ( n ) O(n) O(n)、空间复杂度 O ( n ) O(n) O(n)
- Go代码
- 题目:字符串加法
- 思路分析:定义两指针分别指向两byte数组末尾,从后往前相加,十进制相加余数`=%10`,进位`=/10`
- 复杂度:时间复杂度 O ( m a x ( n , m ) ) O(max(n,m)) O(max(n,m))、空间复杂度 O ( 1 ) O(1) O(1)
- Go代码
- 题目:二进制加法
- 思路分析:定义两指针分别指向两byte数组末尾,从后往前相加,二进制相加余数`=%2`,进位`=/2`
- 复杂度:时间复杂度 O ( m a x ( n , m ) ) O(max(n,m)) O(max(n,m))、空间复杂度 O ( 1 ) O(1) O(1)
- Go代码
- 幂运算专题
- 题目:求2的幂
- 解法1:试除法:循环除2,判断最后值是否==1
- 解法2:`n&(n-1)==0` 或者`n&(-n)==n`
- 解法3:判断n能否被最大2的幂整除(判断n是否为最大2的幂的约数)
- 题目:求3的幂
- 解法1:试除法:循环除3,判断最后是否==1
- 解法2:判断n能否被最大3的幂整除(判断n是否为最大3的幂的约数)
- 题目:求4的幂
- 解法1:试除法:循环除4,判断最后是否==1
- 解法2:必然是2的幂,二进制时1必然在奇数位上`n&0xaaaaaaaa==0`
- 解法3:必然是2的幂,对3取余为1 `n%3==1`
数组实现加法专题
题目:数组实现整数加法
题目链接:LeetCode-66. 加一

思路分析:数组末尾开始,逐个元素+1,=10就进位,!=10就退出
复杂度:时间复杂度 O ( n ) O(n) O(n)、空间复杂度 O ( n ) O(n) O(n)
Go代码
func plusOne(digits []int) []int {length := len(digits)for i:= length-1; i>=0; i-- {digits[i]++digits[i] = digits[i]%10if digits[i] != 0 {return digits}}ret := make([]int, length+1)ret[0] = 1copy(ret[1:], digits)return ret
}
题目:字符串加法
题目链接:LeetCode-415. 字符串相加

思路分析:定义两指针分别指向两byte数组末尾,从后往前相加,十进制相加余数=%10,进位=/10
复杂度:时间复杂度 O ( m a x ( n , m ) ) O(max(n,m)) O(max(n,m))、空间复杂度 O ( 1 ) O(1) O(1)
Go代码
func addStrings(num1 string, num2 string) string {length1, length2 := len(num1), len(num2)ret := ""for i, j, sign := length1-1, length2-1, 0; i >=0 || j >= 0 || sign>0; i,j = i-1,j-1 {var n1, n2 intif i >= 0 {n1 = getNum(num1[i])}if j >= 0 {n2 = getNum(num2[j])}v := n1 + n2 + signret = strconv.Itoa(v%10) + retsign = v/10}return ret
}
func getNum(str byte) int {return int(str-'0')
}
题目:二进制加法
题目链接:LeetCode-LCR 002. 二进制求和

思路分析:定义两指针分别指向两byte数组末尾,从后往前相加,二进制相加余数=%2,进位=/2
复杂度:时间复杂度 O ( m a x ( n , m ) ) O(max(n,m)) O(max(n,m))、空间复杂度 O ( 1 ) O(1) O(1)
Go代码
func addBinary(a string, b string) string {length1, length2 := len(a), len(b)str := ""for i,j,sign := length1-1, length2-1, 0; i>=0 || j>=0 || sign>0; i,j = i-1,j-1{var n1, n2 intif i >= 0 {n1 = int(a[i]-'0')}if j >= 0 {n2 = int(b[j]-'0')}v := n1 + n2 + signstr = strconv.Itoa(v%2) + strsign = v/2}return str
}
幂运算专题
题目:求2的幂
题目链接:LeetCode-231. 2 的幂

解法1:试除法:循环除2,判断最后值是否==1
复杂度:时间复杂度 O ( l o g n ) O(log n) O(logn)、空间复杂度 O ( 1 ) O(1) O(1)
Go代码
func isPowerOfTwo(n int) bool {if n <= 0 {return false}for n%2==0 {n = n/2}return n==1
}
解法2:n&(n-1)==0 或者n&(-n)==n
如果存在非负整数k使得 n=2^k,则n的二进制表示为1后面跟k个0。
所以,正整数n是2的幂,当且仅当n的二进制表示中只有最高位是1,其余位都是0,此时满足 n&(n-1)=0
复杂度:时间复杂度 O ( 1 ) O(1) O(1)、空间复杂度 O ( 1 ) O(1) O(1)
Go代码
func isPowerOfTwo(n int) bool {return n>0 && n&(n-1)==0
}
func isPowerOfTwo(n int) bool {return n>0 && n&(-n)==n
}
解法3:判断n能否被最大2的幂整除(判断n是否为最大2的幂的约数)
复杂度:时间复杂度 O ( 1 ) O(1) O(1)、空间复杂度 O ( 1 ) O(1) O(1)
Go代码
func isPowerOfTwo(n int) bool {max := 1<<30return n>0 && max%n == 0
}
题目:求3的幂
题目链接:LeetCode-326. 3 的幂

解法1:试除法:循环除3,判断最后是否==1
复杂度:时间复杂度 O ( l o g n ) O(log n) O(logn)、空间复杂度 O ( 1 ) O(1) O(1)
Go代码
func isPowerOfThree(n int) bool {if n <= 0 {return false}for n%3==0 {n = n/3}return n == 1
}
解法2:判断n能否被最大3的幂整除(判断n是否为最大3的幂的约数)
在32位有符号整数的范围内,最大的3的幂为3^19=1162261467,判断n是否能被该数整除,即n是否是该数的约数即可。
复杂度:时间复杂度 O ( 1 ) O(1) O(1)、空间复杂度 O ( 1 ) O(1) O(1)
Go代码
func isPowerOfThree(n int) bool {return n>0 && 1162261467%n==0
}
题目:求4的幂
题目链接:LeetCode-342. 4的幂

解法1:试除法:循环除4,判断最后是否==1
复杂度:时间复杂度 O ( l o g n ) O(log n) O(logn)、空间复杂度 O ( 1 ) O(1) O(1)
Go代码
func isPowerOfFour(n int) bool {if n <= 0 {return false}for n%4 == 0 {n = n/4}return n==1
}
解法2:必然是2的幂,二进制时1必然在奇数位上n&0xaaaaaaaa==0
4 的一些幂次的二进制表示:
4^0 = 1,二进制表示:0001
4^1 = 4,二进制表示:0100
4^2 = 16,二进制表示:10000
4^3 = 64,二进制表示:1000000
…
这些幂次的二进制表示中,只有一个位是 1,而且这个 1 总是出现在奇数的位置上(从右数,从 0 开始计数)
复杂度:时间复杂度 O ( 1 ) O(1) O(1)、空间复杂度 O ( 1 ) O(1) O(1)
Go代码
func isPowerOfFour(n int) bool {return n > 0 && n & (n-1) == 0 && (n & 0xaaaaaaaa) == 0
}
解法3:必然是2的幂,对3取余为1 n%3==1
一个整数 n 对 3 取余的结果只可能是 0、1 或 2。如果一个数的二进制表示中只有一个位是 1,并且这个 1 出现在奇数的位置上,那么这个数对 3 取余的结果就是 1。
复杂度:时间复杂度 O ( 1 ) O(1) O(1)、空间复杂度 O ( 1 ) O(1) O(1)
Go代码
func isPowerOfFour(n int) bool {return n > 0 && n & (-n)==n && n%3==1
}
相关文章:

[Go版]算法通关村第十三关白银——数字数学问题之数组实现加法、幂运算
目录 数组实现加法专题题目:数组实现整数加法思路分析:数组末尾开始,逐个元素1,10就进位,!10就退出复杂度:时间复杂度 O ( n ) O(n) O(n)、空间复杂度 O ( n ) O(n) O(n)Go代码 题目:字符串加法…...
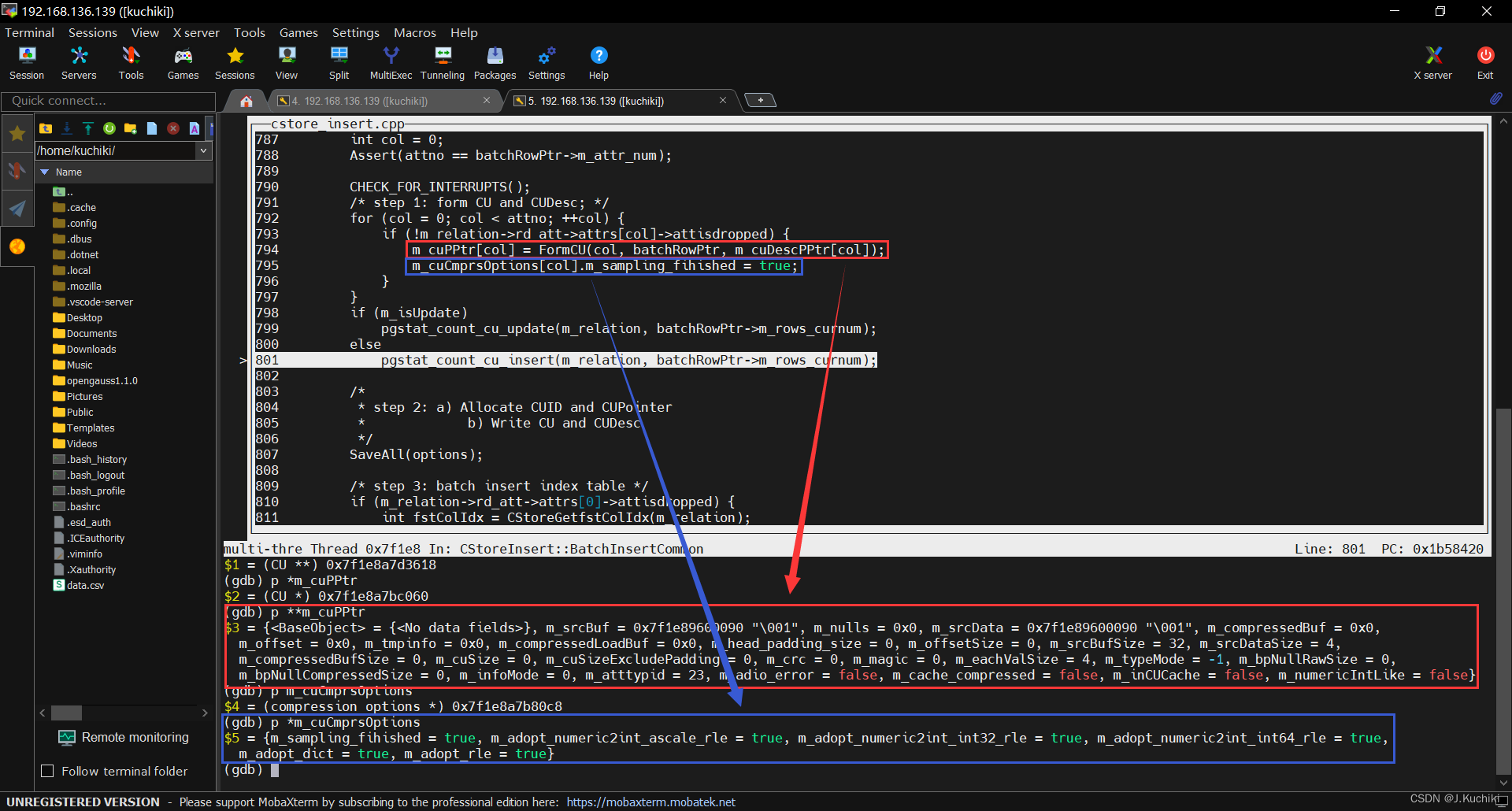
【 OpenGauss源码学习 —— 列存储(Insert)】
列存储(Insert) 概述相关函数ExecInsertRelationData 结构体FormData_pg_class 结构体HeapInsertCStore函数InsertArg 结构体CStoreInsert 类CStoreInsert::InitInsertArg函数heap_deform_tuple 函数bulkload_rows 结构体append_one_tuple 函数bulkload_…...

Android 13.0 framework中实现默认长按电源键弹出关机对话框功能
1.前言 在13.0的系统定制化开发中,在12.0的系统之前默认的都是长按电源键弹出关机对话框,而在13以后 就改成音量+电源键弹出对话框,由于使用不方便,所以就改成默认长按弹出关机对话框功能 2.framework中实现默认长按电源键弹出关机对话框功能的核心类 frameworks/base/s…...
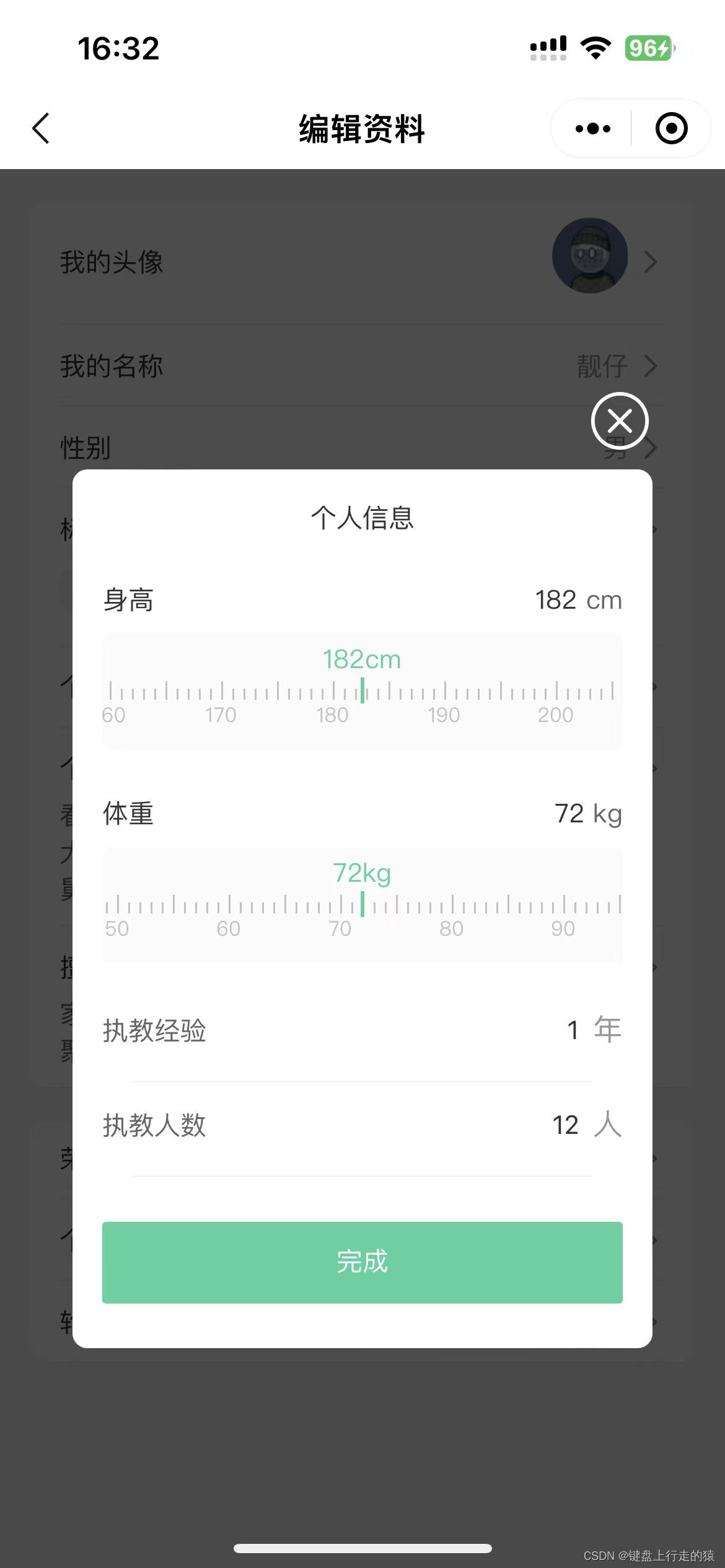
微信小程序,封装身高体重选择器组件
wxml代码: // 微信小程序的插值语法不支持直接使用Math <wxs src"./ruler.wxs" module"math"></wxs> <view class"ruler-container"><scroll-view scroll-left"{{scrollLeft}}" enhanced"{{tru…...

深度学习调参技巧
写完代码—> 小数据上降loss无nan—> 大数据没爆卡速度可以—> 实验log完好可视化loss稳步下降—>回头看实验结果 写完代码后,不要只是在小数据上降loss无nan,还要检查一下模型的输出是否符合预期,比如是否有明显的偏差或者异常值…...
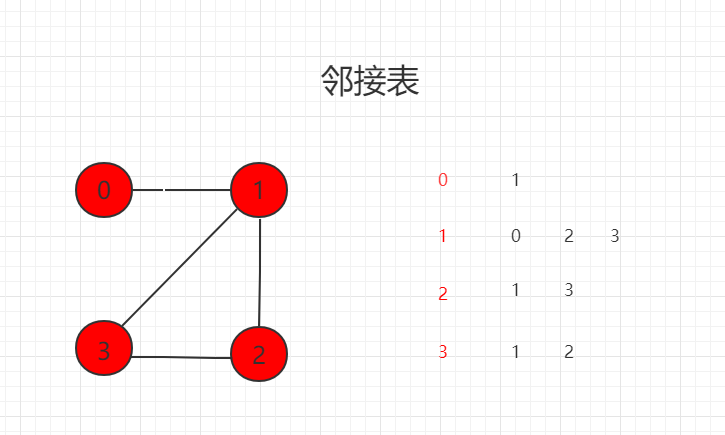
图论基础和表示(Java 实例代码)
目录 图论基础和表示 一、概念及其介绍 二、适用说明 三、图的表达形式 Java 实例代码 src/runoob/graph/DenseGraph.java 文件代码: src/runoob/graph/SparseGraph.java 文件代码: 图论基础和表示 一、概念及其介绍 图论(Graph Theory)是离散数…...

各种数据库查询报错问题
文章目录 前言一、约束条件是自增,不能直接添加数据二、使用步骤1.引入库2.读入数据 总结 前言 记录常见的数据库使用问题,以及对应解决思路 一、约束条件是自增,不能直接添加数据 消息 8101,级别 16,状态 1…...

人效九宫格城市沙龙暨《人效九宫格白皮书》发布会 —上海站,圆满结束
8月11日,在上海龙之梦万丽酒店,由盖雅工场主办的人效九宫格城市沙龙暨《人效九宫格白皮书》发布会 —上海站,圆满结束。 近百位来自多个行业的企业管理者及人力资源从业者汇聚一堂,共同探讨企业如何将盈利模式从数量增长转为质量增…...

【C语言】文件操作 -- 详解
一、什么是文件 磁盘上的文件是文件。 1、为什么要使用文件 举个例子,当我们想实现一个 “通讯录” 程序时,在通讯录中新建联系人、删除联系人等一系列操作,此时的数据存储于内存中,程序退出后所有数据都会随之消失。为了让通讯录…...

飞天使-k8s基础组件分析-持久化存储
文章目录 emptyDirhostpathpv和pvc介绍nfs作为静态pv案例nfs作为动态pv案例使用本地文件夹作为pv改变默认存储类及回收策略参考文档 emptyDir 重启文件还有,但是如果杀了进程,则会丢失文件 创建pod # kubectl apply –f redis.yaml校验pod是否处于运行&…...
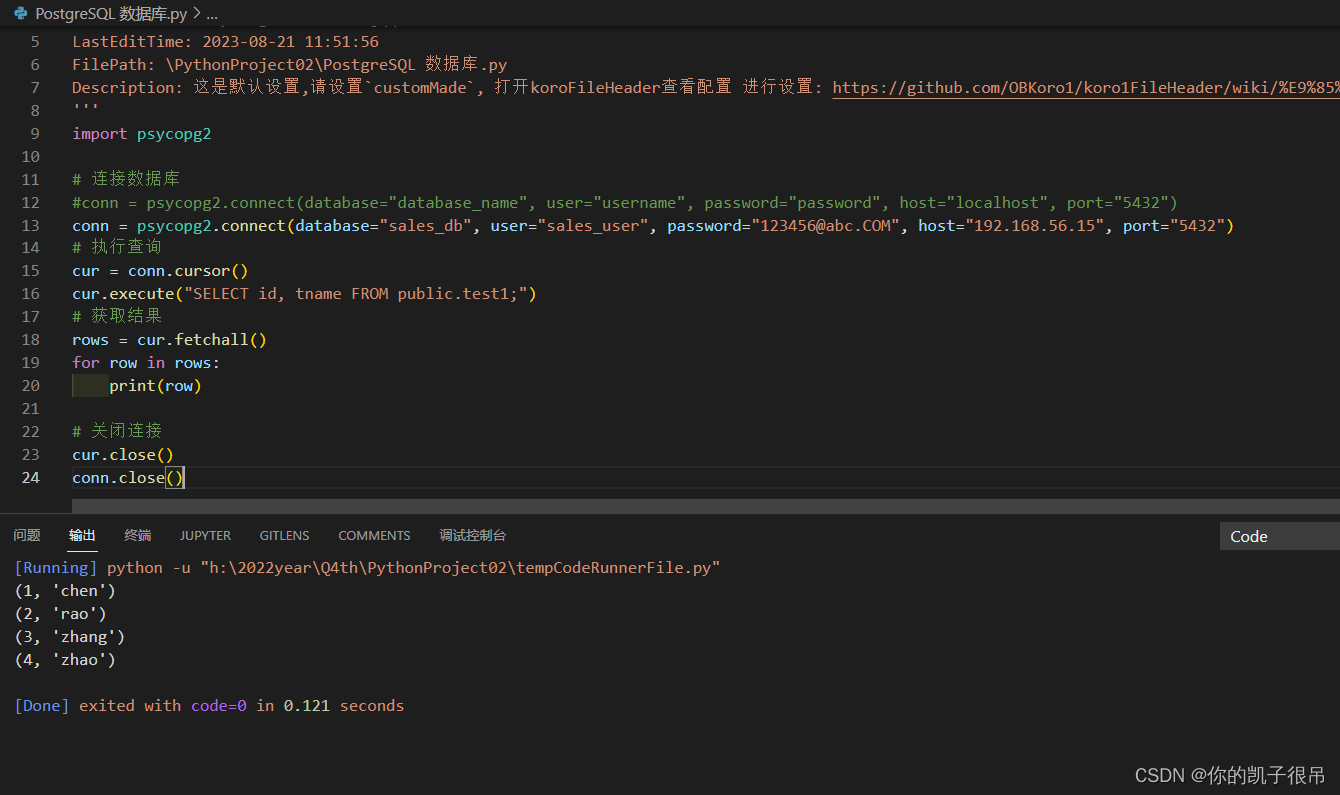
python连接PostgreSQL 数据库
执行如下命令安装 pip3 install psycopg2 python代码 Author: tkhywang 2810248865qq.com Date: 2023-08-21 11:42:17 LastEditors: tkhywang 2810248865qq.com LastEditTime: 2023-08-21 11:51:56 FilePath: \PythonProject02\PostgreSQL 数据库.py Description: 这是默认设置…...
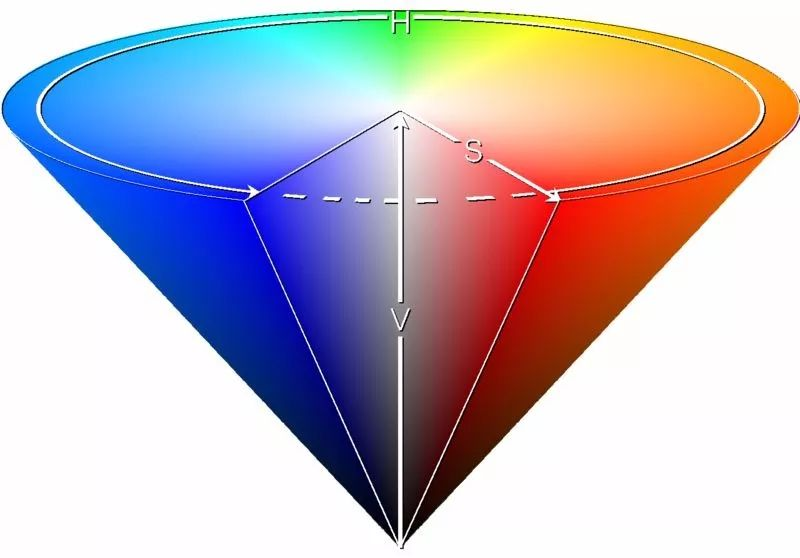
数字图像处理—— Lab、YCbCr、HSV、RGB之间互转
Lab “Lab” 图像格式通常指的是 CIELAB 色彩空间,也称为 Lab 色彩空间。它是一种用于描述人类视觉感知的颜色的设备无关色彩空间,与常见的 RGB 和 CMYK 色彩空间不同。CIELAB 由国际照明委员会(CIE)于1976年定义,用于…...

自动驾驶SLAM技术第四章习题2
在g2o的基础上改成ceres优化,高博都写好了其他的部分, 后面改ceres就很简单了. 这块我用的是ceres的自动求导,很方便,就是转化为模板仿函数的时候有点麻烦, 代码部分如下 ceres_type.h : ceres优化核心库的头文件 这个文件写的内…...

vue拖拽div盒子实现上下拖动互换
vue拖拽div盒子实现上下拖动互换 <div v-for"(item, index) in formList" :key"index" draggable"true"dragstart"handleDragStart($event, item)"dragenter"handleDragEnter($event, item)"dragover.prevent"han…...
Visual Studio 2022 右键单击项目没有出现View | View Class Diagram(Visual Studio 无法使用类设计器)
文章目录 问题描述原因.NET Core项目.NET Framework项目 问题描述 当我们在Solution Explorer窗口右键单击项目时,快捷菜单中没有出现“查看”,或者出现了“查看”,但是“查看”里没有View Class Diagram。 原因 首先你要确保你安装了类设…...

EFCore常见用法
EFCore官方文档置顶,看这个就行。下面的内容只是总结,算是备忘录。 一、创建和删除 //1、创建数据库和表 db.Database.EnsureCreated();//将创建数据库(如果不存在)并初始化数据库架构。 如果存在任何表 (包括另一 DbContext 类)…...

概率论与数理统计:第六章:数理统计
文章目录 Ch6. 数理统计(一) 总体与样本(二) 统计量 (5个)2.5个常用统计量3.矩的概念 (三) 抽样分布 (3个)0.上α分位点1.χ分布2.t分布3.F分布 (四) 抽样分布定理1.单个正态总体2.两个正态总体 Ch6. 数理统计 (一) 总体与样本 1.概念: (1)总体 (2)样本 简单随机…...
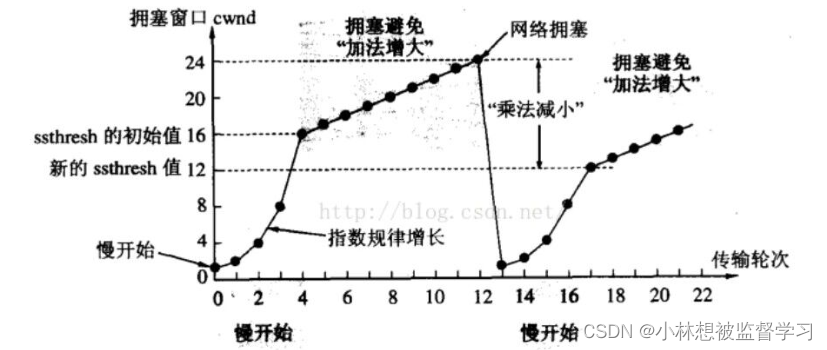
拥塞控制(TCP限制窗口大小的机制)
拥塞控制机制可以使滑动窗口在保证可靠性的前提下,提高传输效率 关于滑动窗口的属性以及部分机制推荐看TCP中窗口和滑动窗口的含义以及流量控制 拥塞控制出现的原因 看了上面推荐的博客我们已经知道了,由于接收方接收数据的能力有限,所以要通…...

校园供水系统智能管理
import pandas as pd data1pd.read_excel("C://Users//JJH//Desktop//E//附件_一季度.xlsx") data2pd.read_excel("C://Users//JJH//Desktop//E//附件_二季度.xlsx") data3pd.read_excel("C://Users//JJH//Desktop//E//附件_三季度.xlsx") data4…...

Flask-SocketIO和Flask-Login联合开发socketio权限系统
设置 Flask, Flask-SocketIO, Flask-Login: 首先,确保安装了必要的库: pip install Flask Flask-SocketIO Flask-Login基础设置: from flask import Flask, render_template, redirect, url_for, request from flask_socketio import SocketIO, emit from flask_…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
