当前位置： 首页 > news >正文

Pycharm链接远程mysql报错

news 2025/10/27 11:51:31

Pycharm链接远程mysql配置及相应报错如下：

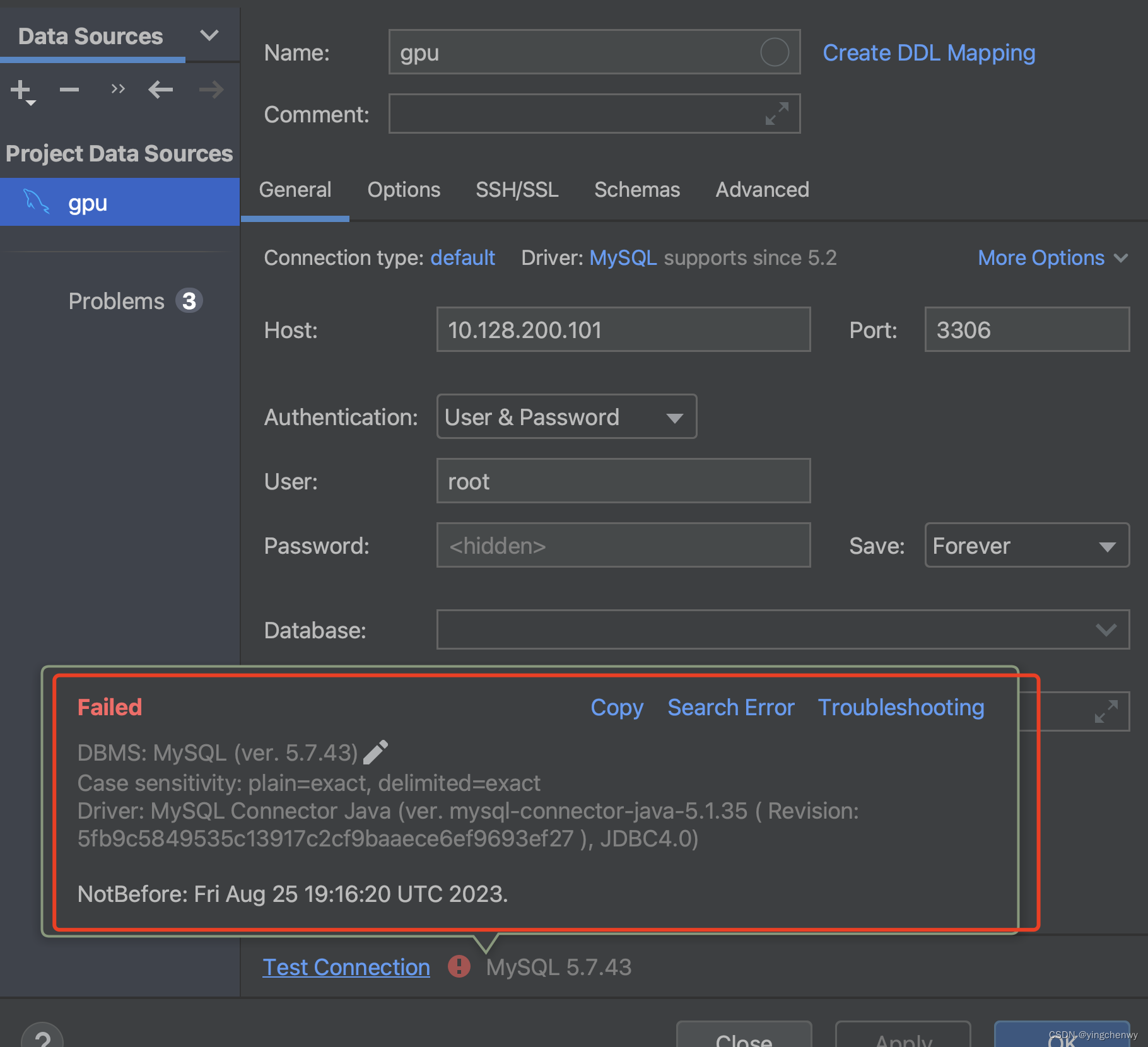
解决方法：

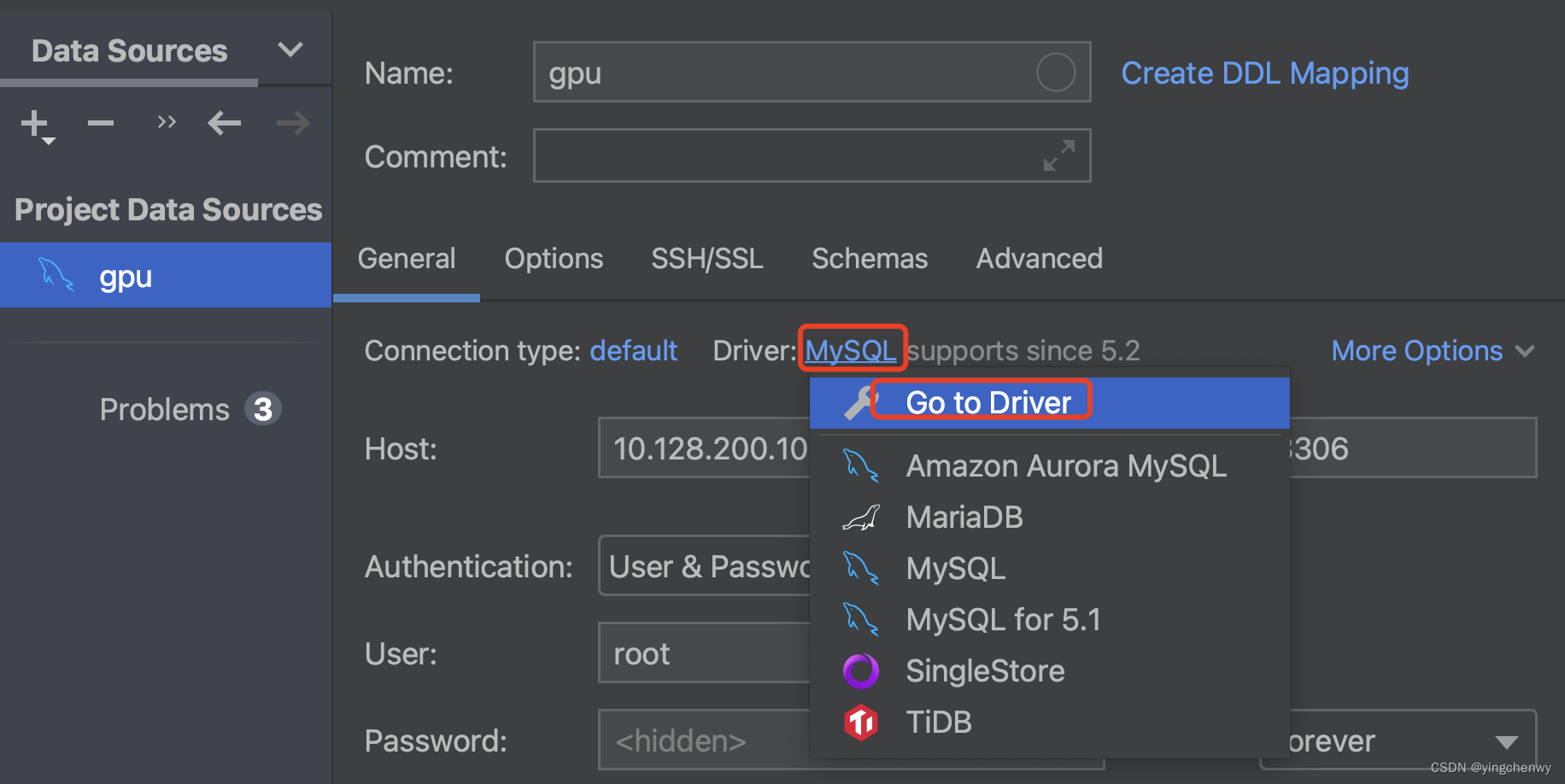
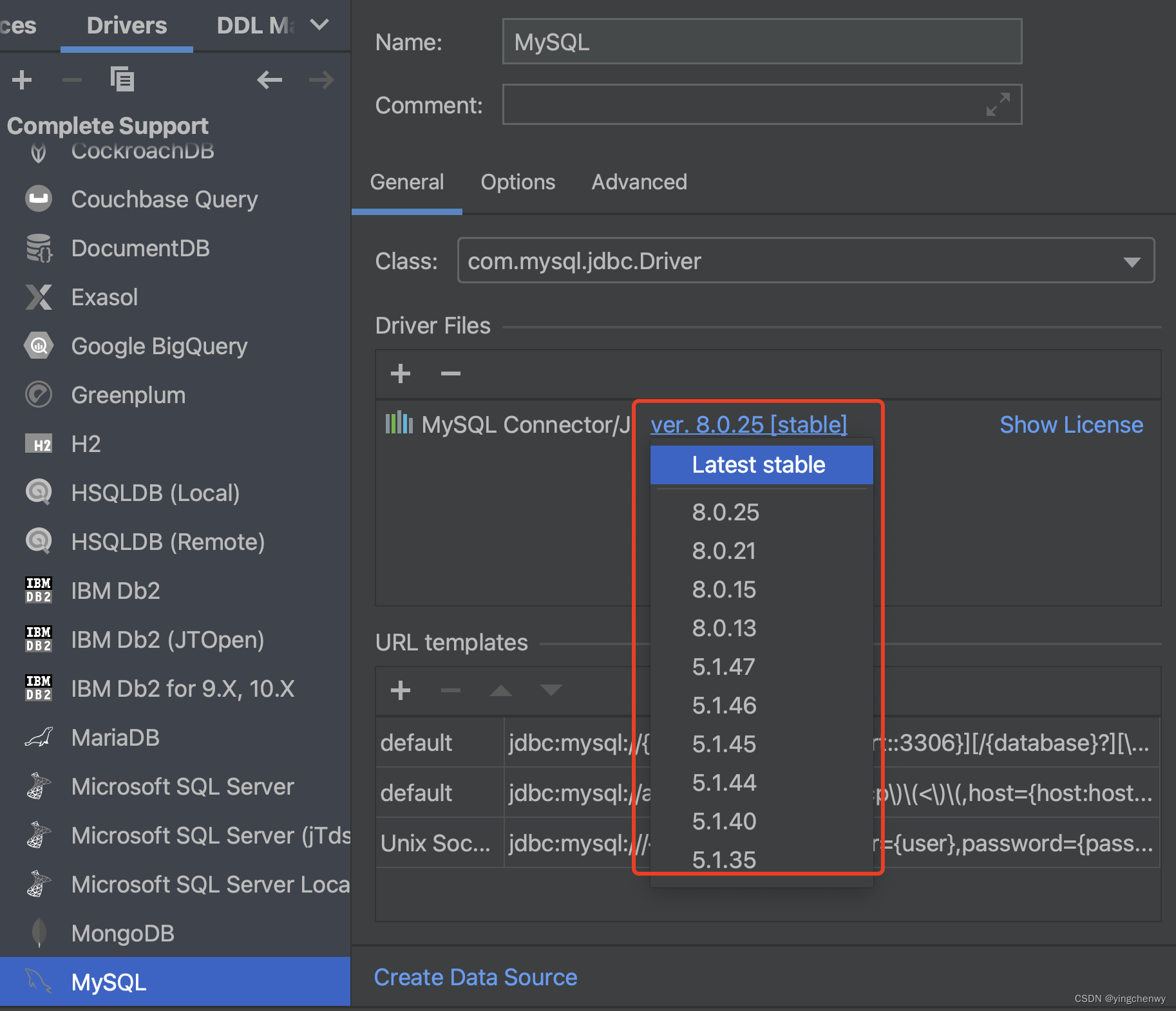
去服务器确认Mysql版本号：

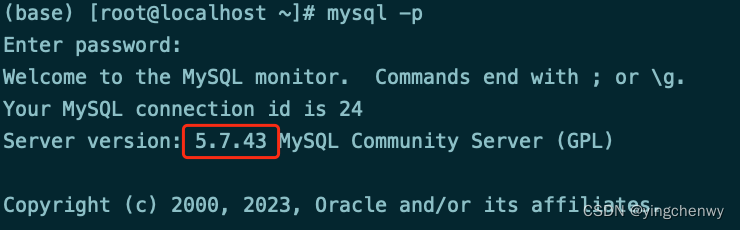
我的Mysql为5.7.43，此时Pycharm mysql驱动为8.0版本，不匹配，所以需要根据实际的版本选择对应的驱动；选择对应的版本，在大版本一直的情况下，可逐个尝试，此处我选择的是5.1.35； 

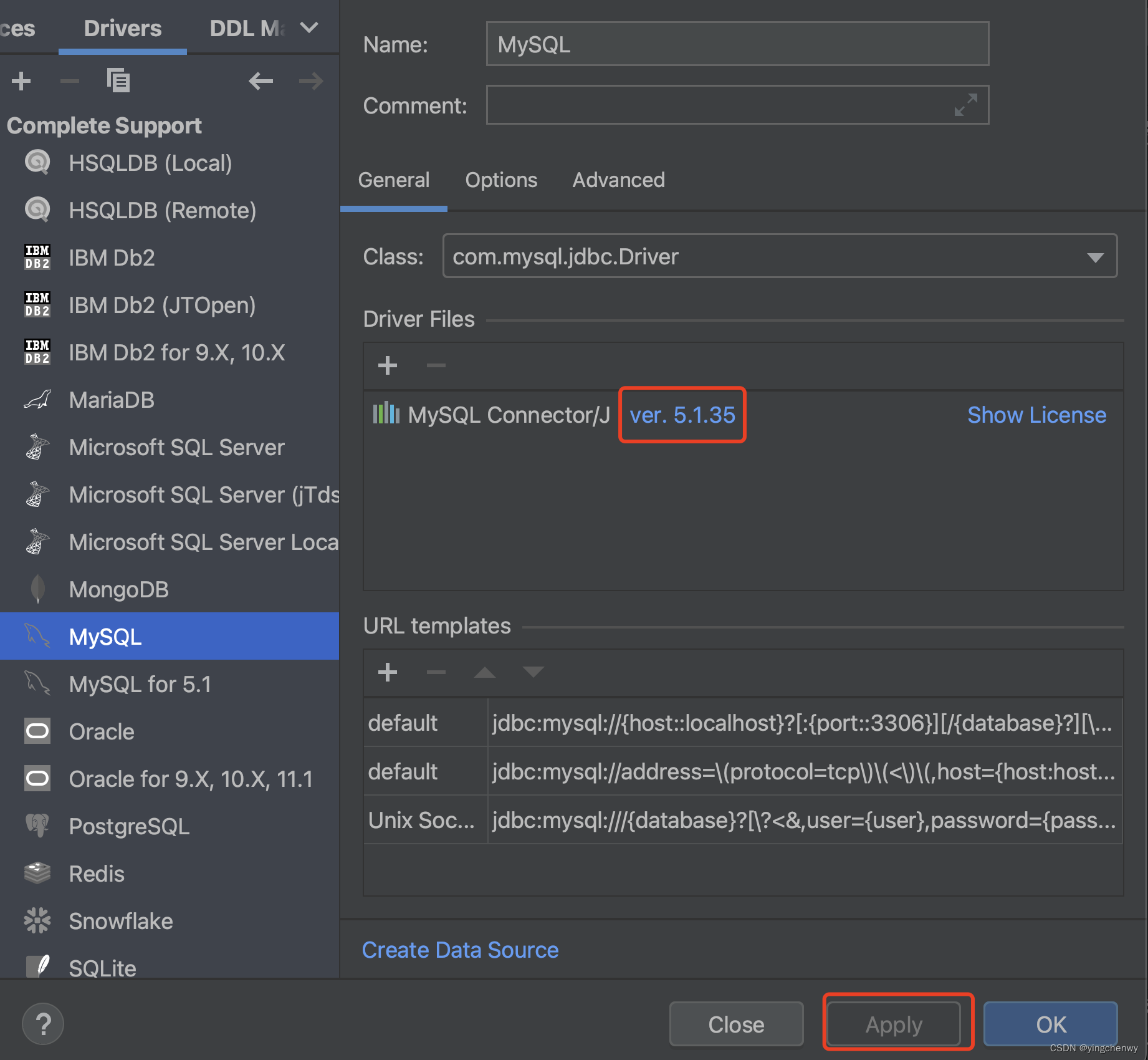
点击下方Apply；

回到DataSource配置，重新测试链接，可以看到成功链接 

 

 

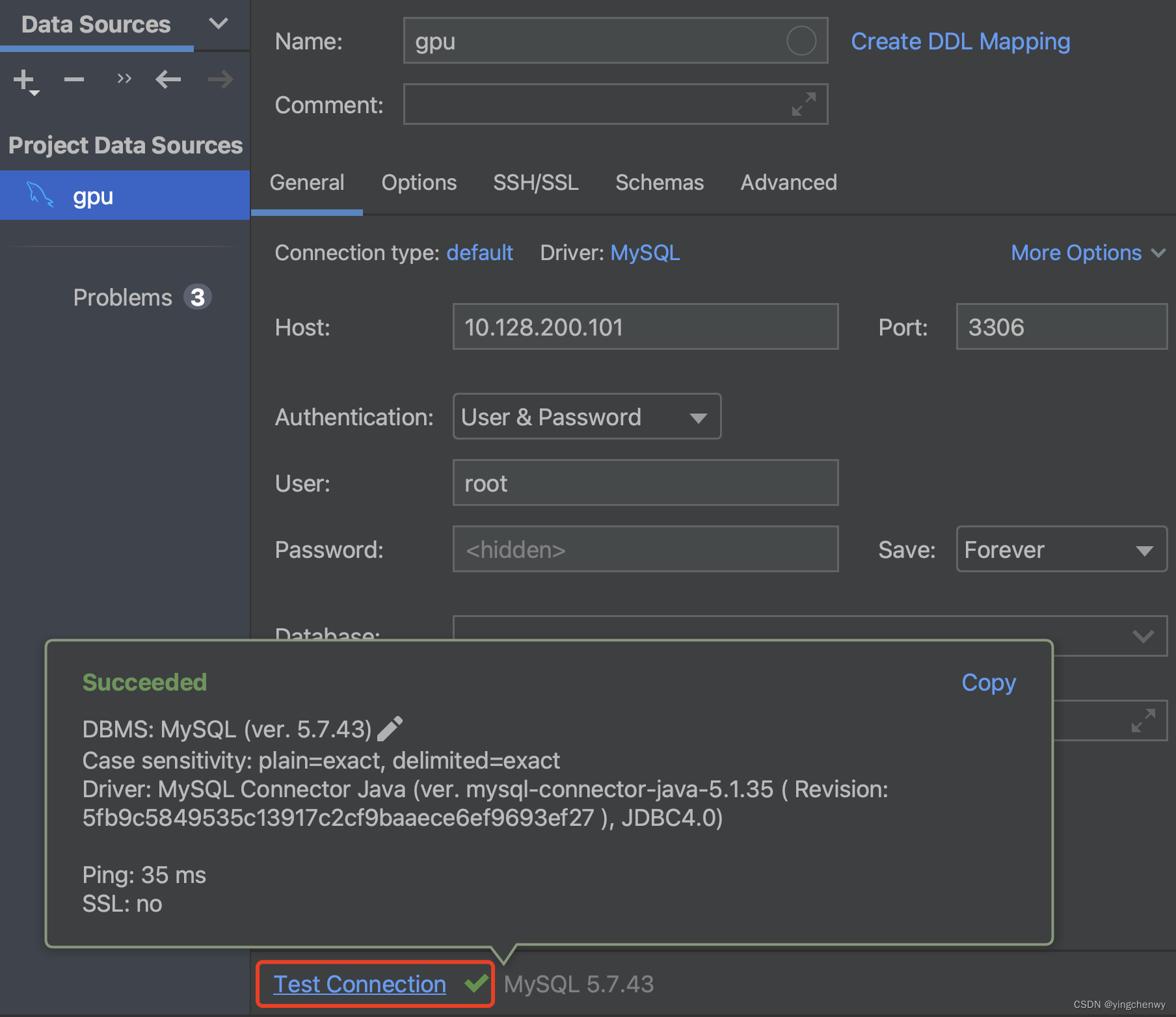
相关文章：

Pycharm链接远程mysql报错

Pycharm链接远程mysql配置及相应报错如下： 解决方法： 去服务器确认Mysql版本号： 我的Mysql为5.7.43，此时Pycharm mysql驱动为8.0版本，不匹配，所以需要根据实际的版本选择对应的驱动；选择对应的版…...

编程日记 2023/8/27 1:20:25

【硕士论文完美复现】【价格型需求响应】基于需求侧响应的配电网供电能力综合评估（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。 ⛳️座右铭&a…...

编程日记 2023/8/27 1:19:23

Android Okhttp 源码浅析三

核心方法 getResponseWithInterceptorChain() internal fun getResponseWithInterceptorChain(): Response {// Build a full stack of interceptors.val interceptors mutableListOf<Interceptor>()interceptors client.interceptorsinterceptors RetryAndFollowUpI…...

编程日记 2023/8/27 1:18:18

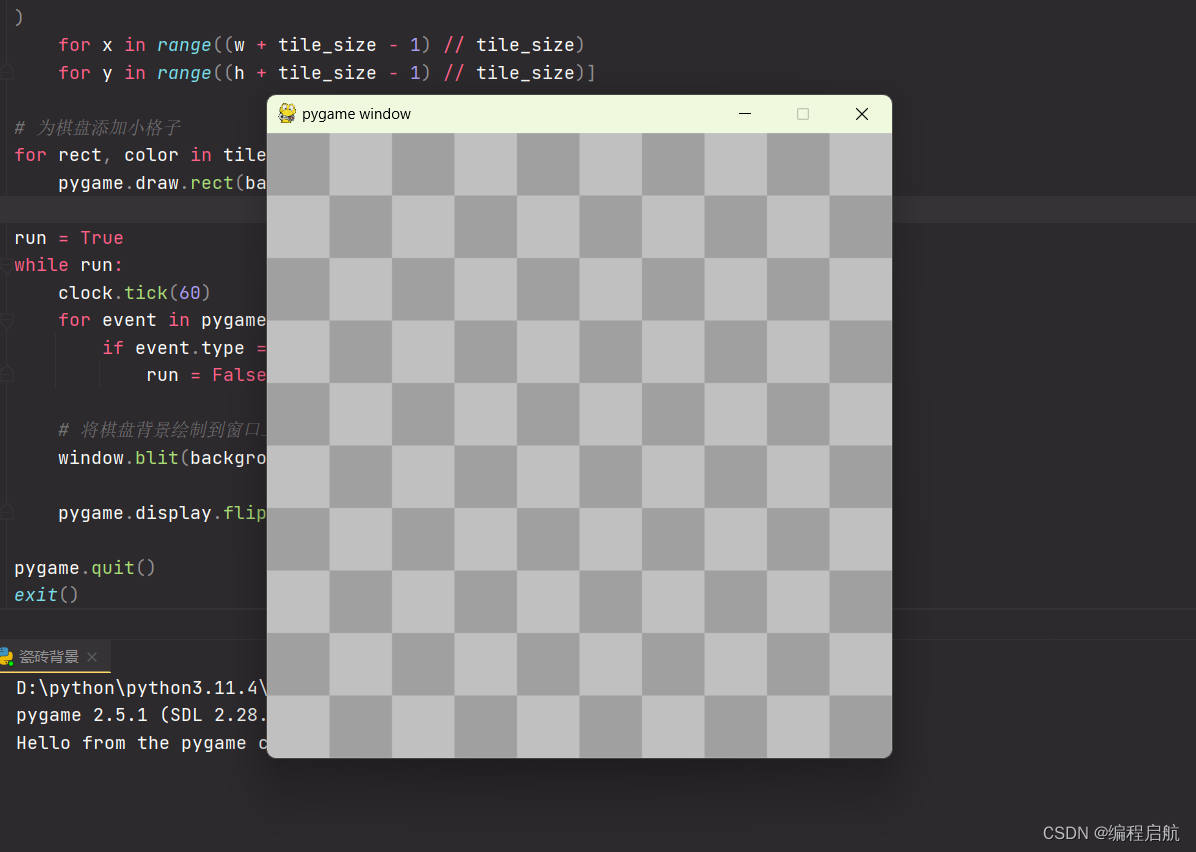
一分钟学会用pygame制作棋盘背景

一分钟一个Pygame案例&#xff0c;这一集我们来学习一下如何生成一个视频中的棋盘背景效果&#xff0c;非常非常简单。 视频教程链接&#xff1a;https://www.bilibili.com/video/BV17G411d7Ah/ 当然我们这里是用来做页面的背景&#xff0c;你也可以拿来做别的效果&#xff0…...

编程日记 2023/8/27 1:17:17

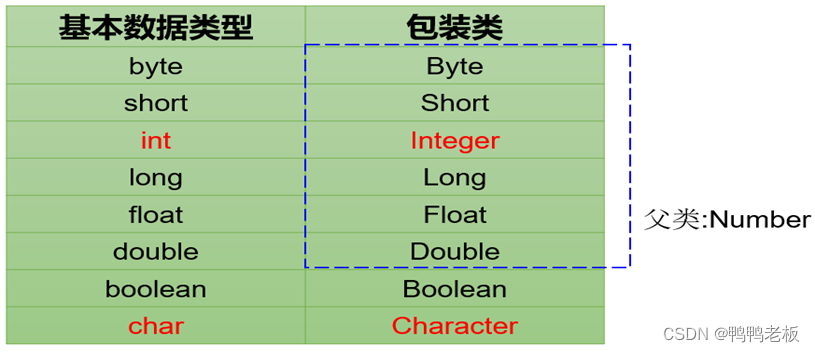
Java --- 包装类

一、包装类 Java针对八种基本数据类型定义了相应的引用类型&#xff1a;包装类&#xff08;封装类&#xff09;。 二、基本数据类型与包装类的基本转换 public class WrapperTest {public static void main(String[] args) {//基本数据类型转换为包装类Boolean aBoolean new…...

编程日记 2023/8/27 1:16:15

[运维] wvp 28181安装部署全流程(ubuntu2204)

部署wvp 系统环境 系统版本&#xff1a;ubuntu2204 安装相关工具 sudo apt update ## 编译工具 sudo apt install git openjdk-11-jdk tar vim cmake gcc g libsrtp2-dev libssl-dev ## ffmepg sudo apt install ffmpeg编译zlm 编译zlm git clone https://gitee.com/xia-…...

编程日记 2023/8/27 1:15:15

vue实现富文本

效果图展示 一、安装依赖 npm install vue-quill-editor --save二、具体使用 html <template><!-- 富文本 --><quill-editorref"myQuillEditor"v-model"content":options"editorOption"blur"onEditorBlur($event)"…...

编程日记 2023/8/27 1:14:12

uniapp 开发微信小程序使用echart的dataZoom属性缩放功能不生效！bug记录！

在本项目中使用的是这个echart库 在项目中添加了dataZoom配置项但是不生效&#xff0c;突然想到微信小程序代码大小的限制&#xff0c;之前的echarts.js是定制的&#xff0c;有可能没有加dataZoom组件。故重新定制echarts.js。之前用的echarts版本是5.0.0&#xff0c;这次也是…...

编程日记 2023/8/27 1:13:11

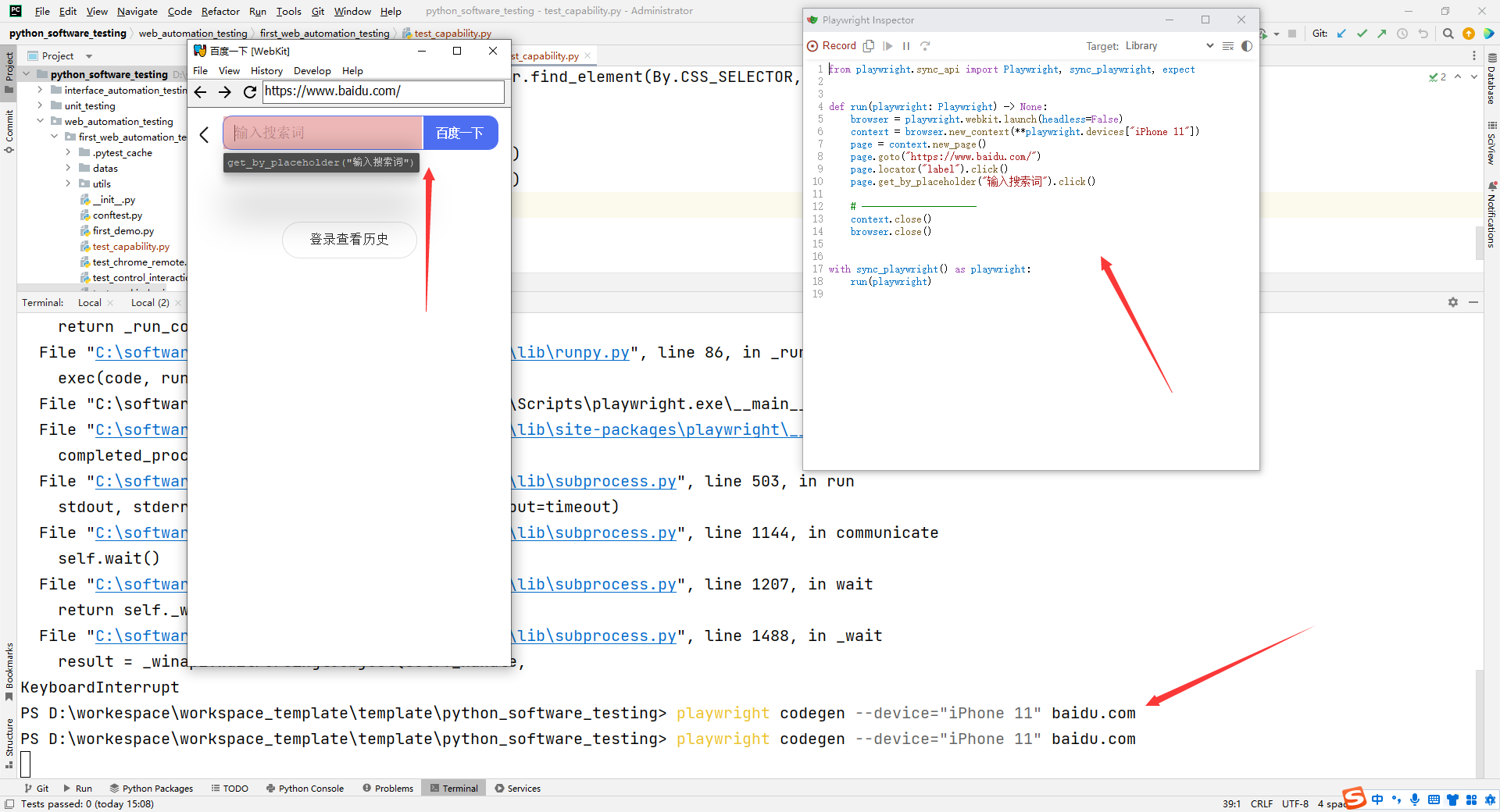
用户端Web自动化测试_L4

目录&#xff1a; selenium多浏览器处理执行 javascript 脚本headless无头浏览器使用capability配置参数解析企业微信实战cypress测试框架介绍Playwright测试框架介绍 1.selenium多浏览器处理 多浏览器测试背景 用户使用的浏览器(firefox,chrome,IE 等)web 应用应该能在任何…...

编程日记 2023/8/27 1:12:06

CAPL - Panel和TestModule结合实现测试项可选

目录 一、定义脚本编号和脚本组编号 1、测试组定义 2、测试脚本编号定义...

编程日记 2023/8/27 1:11:05

机器学习,过拟合与欠拟合,正则化与交叉验证

目录 机器学习 过拟合与欠拟合 正则化与交叉验证 正则化 交叉验证 机器学习 的目的是使学到的模型不仅对已知数据而且对未知数据都能有很好的预测能力。 不同的机器学习方法会给出不同的模型。当损失函数给定时&#xff0c;基于损失函数的模型的训练误差&#xff08;tra…...

编程日记 2023/8/27 1:08:59

gradio使用transformer模块demo介绍1：Text Natural Language Processing

文章目录 文本生成 Text Generation自动完成 Autocomplete情感分析 Sentiment Analysis命名实体识别 Name Entity Recognition NER多语种翻译文本生成 Text Generation import gradio as gr from transformers import pipelinegenerator = pipeline(text-generation, model=&l…...

编程日记 2023/8/27 1:07:58

算法通关村——数论经典问题解析

1. 辗转相除法 主要目的是获取两个数里面的最大公约数。 public int gcd(int a, int b) {int k 0;do {k a % b;a b;b k;} while (k ! 0);return a;}2. 素数和合数 素数的要求是必须大于等于2&#xff0c;并且只能被1和它本身整除。 判断的方法比较简单&#xff0c;就是从…...

编程日记 2023/8/27 1:06:56

代码随想录算法训练营第四十六天|LeetCode 1143，1035，53

目录 LeetCode 1143.最长公共子序列 动态规划五步曲&#xff1a; 1.确定dp[i][j]的含义 2.找出递推公式 3.初始化dp数组 4.确定遍历顺序 5.打印dp数组 LeetCode 1035.不相交的线 LeetCode 53.最大子序列和&#xff08;动态规划&#xff09; 动态规划五步曲&#xff1a; 1.确定…...

编程日记 2023/8/27 1:05:54

leetcode 541.反转字符串II

⭐️ 题目描述 &#x1f31f; leetcode链接&#xff1a;https://leetcode.cn/problems/reverse-string-ii/ ps&#xff1a; 这道题描述的有点晦涩难懂&#xff0c;意思就是每隔k个反转k个&#xff0c;末尾不够k个时全部反转&#xff0c;开始就不够k个也全部反转。 代码&#…...

编程日记 2023/8/27 1:04:53

MyBatis与Spring整合以及AOP和PageHelper分页插件整合

目录 前言 一、MyBatis与Spring整合的好处以及两者之间的关系 1.好处 2.关系 二、MyBatis和Spring集成 1.导入pom.xml 2.编写配置文件 3.利用mybatis逆向工程生成模型层代码 三、常用注解 四、AOP整合pageHelper分页插件 创建一个切面 测试 前言 MyBatis是一个开源的…...

编程日记 2023/8/27 1:03:52

《认知觉醒》读书笔记之潜意识

模糊--人生是一场消除模糊的比赛。 学习知识&#xff0c;消除认知模糊 掌握的工具越多&#xff0c;认知能力越强&#xff0c;消除模糊的能力就越强。 元认知-----》 如何反观自己。 刻意练习----》 如何精进自己。 运动改造大脑---》 如何激化自己的运动热情。 学习知识的…...

编程日记 2023/8/27 1:02:51

Stable Diffusion 系列教程 | 图生图基础

前段时间有一个风靡全网的真人转漫画风格&#xff0c;受到了大家的喜欢 而在SD里&#xff0c;就可以通过图生图来实现类似的效果 当然图生图还有更好玩的应用&#xff0c;我们一点一点来探索 首先我们来简单进行一下图生图的这一个实践---真人转动漫 1. 图生图基本界面 和…...

编程日记 2023/8/27 1:01:49

cuda编程day001

一、环境&#xff1a; ①、linux cuda-11.3 opecv4.8.0 不知道头文件和库文件路径&#xff0c;用命令查找&#xff1a; # find /usr/local -name cuda.h 2>/dev/null # 查询cuda头文件路径 /usr/local/cuda-11.3/targets/x86_64-linux/include/cuda.h # find /usr/…...

编程日记 2023/8/27 1:00:48

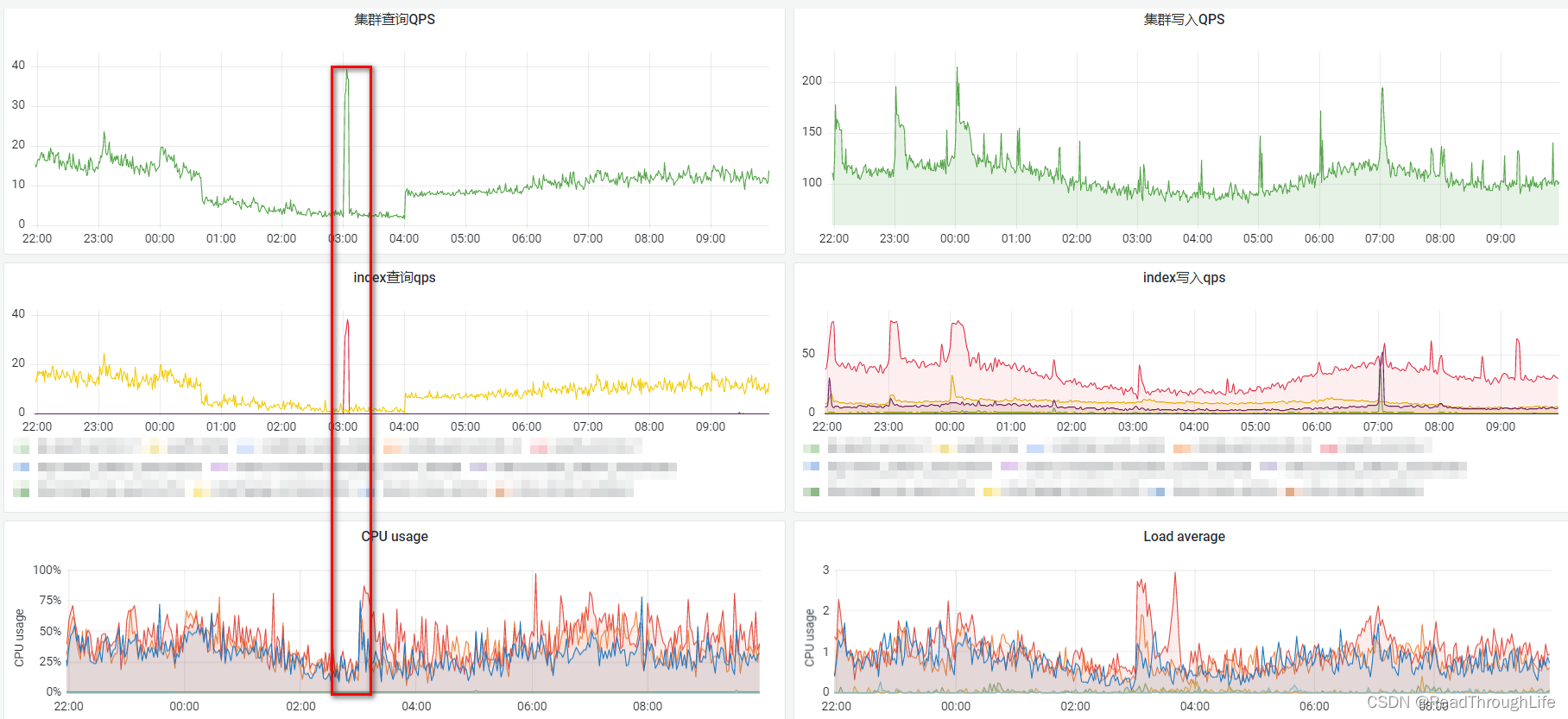
Java 中使用 ES 高级客户端库 RestHighLevelClient 清理百万级规模历史数据

&#x1f389;工作中遇到这样一个需求场景&#xff1a;由于ES数据库中历史数据过多&#xff0c;占用太多的磁盘空间&#xff0c;需要定期地进行清理&#xff0c;在一定程度上可以释放磁盘空间&#xff0c;减轻磁盘空间压力。 &#x1f388;在经过调研之后发现&#xff0c;某服务…...

编程日记 2023/8/27 0:59:46

Linux应用开发之网络套接字编程(实例篇)

服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

编程新知 2025/10/27 0:14:06

生成xcframework

打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式&#xff0c;可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

编程新知 2025/10/5 2:30:38

【网络】每天掌握一个Linux命令 - iftop

在Linux系统中&#xff0c;iftop是网络管理的得力助手&#xff0c;能实时监控网络流量、连接情况等&#xff0c;帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

编程新知 2025/10/10 17:03:53

Objective-C常用命名规范总结

【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名&#xff08;Class Name)2.协议名&#xff08;Protocol Name)3.方法名&#xff08;Method Name)4.属性名&#xff08;Property Name&#xff09;5.局部变量/实例变量&#xff08;Local / Instance Variables&…...

编程新知 2025/10/5 6:41:51

2.Vue编写一个app

1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

编程新知 2025/10/19 19:56:14

Springcloud：Eureka 高可用集群搭建实战（服务注册与发现的底层原理与避坑指南）

引言&#xff1a;为什么 Eureka 依然是存量系统的核心&#xff1f; 尽管 Nacos 等新注册中心崛起&#xff0c;但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制&#xff0c;是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

编程新知 2025/10/26 7:40:30

leetcodeSQL解题：3564. 季节性销售分析

leetcodeSQL解题&#xff1a;3564. 季节性销售分析 题目&#xff1a; 表&#xff1a;sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

编程新知 2025/10/5 19:58:27

优选算法第十二讲：队列 + 宽搜 优先级队列

优选算法第十二讲&#xff1a;队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

编程新知 2025/10/19 15:23:13

AI，如何重构理解、匹配与决策？

AI 时代&#xff0c;我们如何理解消费&#xff1f; 作者&#xff5c;王彬 封面&#xff5c;Unplash 人们通过信息理解世界。 曾几何时&#xff0c;PC 与移动互联网重塑了人们的购物路径&#xff1a;信息变得唾手可得&#xff0c;商品决策变得高度依赖内容。 但 AI 时代的来…...

编程新知 2025/10/24 3:10:00

Bean 作用域有哪些？如何答出技术深度？

导语&#xff1a; Spring 面试绕不开 Bean 的作用域问题&#xff0c;这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开&#xff0c;结合典型面试题及实战场景&#xff0c;帮你厘清重点&#xff0c;打破模板式回答&#xff0c…...

编程新知 2025/7/9 17:59:19