机器学习,过拟合与欠拟合,正则化与交叉验证
目录
机器学习
过拟合与欠拟合
正则化与交叉验证
正则化
交叉验证
机器学习
的目的是使学到的模型不仅对已知数据而且对未知数据都能有很好的预测能力。
不同的机器学习方法会给出不同的模型。当损失函数给定时,基于损失函数的模型的训练误差(training error)和模型的测试误差(test error)就自然成为学习方法评估的标准。
注意,机器学习方法具体采用的损失函数未必是评估时使用的损失函数。当然,让两者一致是比较理想的。


训练误差的大小,对判断给定的问题是不是一个容易学习的问题是有意义的,但是本质上不重要。测试误差反应了学习方法对未知的测试数据集的预测能力。
显然,给定两种学习方法,测试误差小的方法具有更好的预测能力,是更有效的方法。通常讲学习方法对未知数据的预测能力称为泛化能力(generalization ability)。
过拟合与欠拟合
对于机器学习和深度学习模型而言,我们不仅希望它能很好的拟合训练数据集,同时也希望它可以对未知数据集(测试集)有很好的拟合效果(泛化能力)。机器学习的泛化能力(generalization ability)是指由该方法学习到的模型对未知数据的预测能力,是学习方法本质上重要的性质。现实中采用最多的办法是用过测试误差来评价学习方法的泛化能力。
度量泛化能力的好坏,就涉及到所谓的模型的欠拟合(underfitting)和过拟合(overfitting)。
- 过拟合指的是在训练数据集上表现良好,而在未知数据上表现差。
- 欠拟合指的是模型没有很好地学习到数据特征,不能够很好地拟合数据,在训练数据和未知数据上表现都很差。
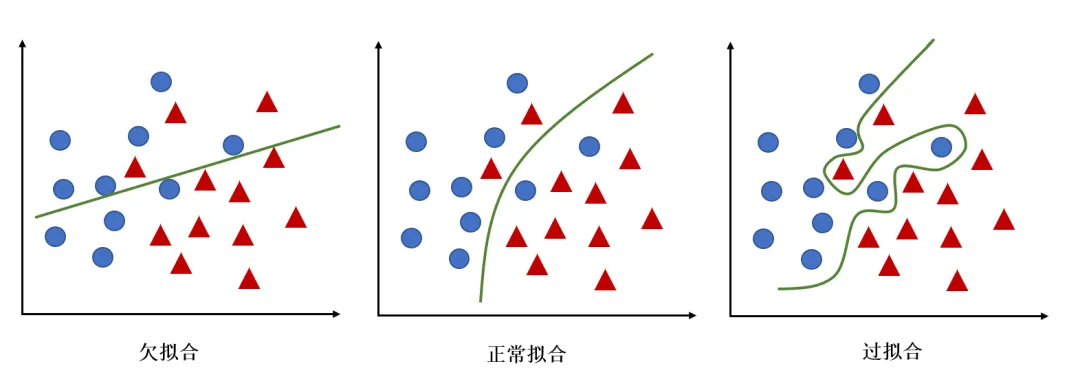
欠拟合、正常拟合和过拟合
下图描述了训练误差和测试误差与模型的复杂度之间的关系。当模型的复杂度增大时,训练误差会逐渐减小并趋近于0;而测试误差会先减小,达到最小值后有增大。当选择的模型复杂度过大时,过拟合现象就会发生。
因此,在学习时就要防止过拟合,进行最优的模型选择,即选择复杂度适当的模型,以达到使测试误差最小的学习目的。
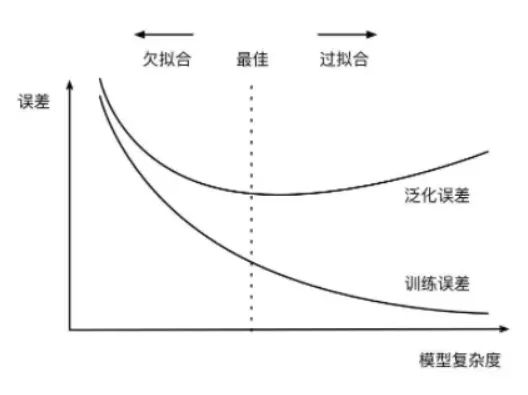
训练误差和测试误差与模型的复杂度之间的关系
过拟合的原因在于:
-
参数太多,模型复杂度过高;
-
建模样本选取有误,导致选取的样本数据不足以代表预定的分类规则;
-
样本噪音干扰过大,使得机器将部分噪音认为是特征从而扰乱了预设的分类规则;
-
假设的模型无法合理存在,或者说是假设成立的条件实际并不成立。
欠拟合的原因在于:
-
特征量过少;
-
模型复杂度过低。
怎么解决过拟合?
-
获取和使用更多的数据(数据集增强)——解决过拟合的根本性方法;
-
特征降维,人工选择保留特征的方法对特征进行降维;
-
加入正则化,控制模型的复杂度;
-
Dropout;(
dropout(随机失活):dropout是通过遍历神经网络每一层的节点,然后通过对该层的神经网络设置一个keep_prob(节点保留概率),即该层的节点有keep_prob的概率被保留,keep_prob的取值范围在0到1之间。通过设置神经网络该层节点的保留概率,使得神经网络不会去偏向于某一个节点(因为该节点有可能被删除),从而使得每一个节点的权重不会过大,有点类似于L2正则化,来减轻神经网络的过拟合。) -
Early stopping;
-
交叉验证。
怎么解决欠拟合?
-
增加新特征,可以考虑加入进特征组合、高次特征,来增大假设空间;
-
添加多项式特征,这个在机器学习算法里面用的很普遍,例如将线性模型通过添加二次项或者三次项使模型泛化能力更强;
-
减少正则化参数,正则化的目的是用来防止过拟合的,但是模型出现了欠拟合,则需要减少正则化参数;
-
使用非线性模型,比如核SVM 、决策树、深度学习等模型;
-
调整模型的容量(capacity),通俗地,模型的容量是指其拟合各种函数的能力;
-
容量低的模型可能很难拟合训练集。
正则化与交叉验证
正则化
模型选择的典型方法是正则化(regularization)。正则化是结构风险最小化策略的实现,是在经验风险上加一个正则化项(regularizer)或惩罚项(penalty term)。正则化项一般是模型复杂度的单调递增函数,模型越复杂,正则化值就越大。比如,正则化项可以是模型参数向量的范数。
正则化一般具有如下形式:

其中,第1项是经验风险,第2项是正则化项, 为调整两者之间关系的系数。

第1项的经验风险较小的模型可能较复杂(有多个非零参数),这时第2项的模型复杂度会较大。正则化的作用是选择经验风险与模型复杂度同时较小的模型。
从贝叶斯估计的角度来看,正则化项对应于 模型的先验概率。
- 可以假设复杂的模型有较小的先验概率
- 简单的模型有较大的先验概率
交叉验证
另一种常用的模型选择方法是交叉验证(cross validation)。
如果给定的样本数据充足,进行模型选择的一种简单方式是随机地将数据集切分成三部分,分别为训练集(training set)、验证集(validation set)和测试集(test set)。训练集用来训练模型,验证集用于模型的选择,测试集用于最终对学习方法的评估。在学习到的不同复杂度的模型中,选择对验证集有最小预测误差的模型。由于验证集有足够多的数据,用它对模型进行选择也是有效的。
但是,在许多实际应用中数据是不充足的。为了选择好模型,可以采用交叉验证方法。交叉验证的基本想法是重复地使用数据;把给定的数据进行切分,讲切分的数据集组合为训练集与测试集,在此基数上反复地进行训练、测试以及模型选择。
-
简单交叉验证
简单交叉验证方法是:首先随机地将已给数据分为两部分,一部分作为训练集,另一部分作为测试集(例如,70%的数据为训练集,30%的数据为测试集);然后用训练集在各种条件下(例如,不同参数个数)训练模型,从而得到不同的模型;在测试集上评价各个模型的测试误差,选出测试误差最小的模型。
-
S折交叉验证
应用最多的是S折交叉验证(S-fold cross validation),方法如下:首先随机地将已给数据切分为S个互不相交、大小相同的子集;然后利用S-1个子集的数据训练模型,利用余下的子集测试模型;将这一过程可能的S种选择重复进行;最后选出S次测评中平均测试误差最小的模型。
-
留一交叉验证
S折交叉验证的特殊情形是S=N,成为留一交叉验证(leave-one-out cross validation,LOOCV),往往在数据缺乏的情况下使用。这里N是给定数据集的容量。
相关文章:

机器学习,过拟合与欠拟合,正则化与交叉验证
目录 机器学习 过拟合与欠拟合 正则化与交叉验证 正则化 交叉验证 机器学习 的目的是使学到的模型不仅对已知数据而且对未知数据都能有很好的预测能力。 不同的机器学习方法会给出不同的模型。当损失函数给定时,基于损失函数的模型的训练误差(tra…...

gradio使用transformer模块demo介绍1:Text Natural Language Processing
文章目录 文本生成 Text Generation自动完成 Autocomplete情感分析 Sentiment Analysis命名实体识别 Name Entity Recognition NER多语种翻译文本生成 Text Generation import gradio as gr from transformers import pipelinegenerator = pipeline(text-generation, model=&l…...

算法通关村——数论经典问题解析
1. 辗转相除法 主要目的是获取两个数里面的最大公约数。 public int gcd(int a, int b) {int k 0;do {k a % b;a b;b k;} while (k ! 0);return a;}2. 素数和合数 素数的要求是必须大于等于2,并且只能被1和它本身整除。 判断的方法比较简单,就是从…...

代码随想录算法训练营第四十六天|LeetCode 1143,1035,53
目录 LeetCode 1143.最长公共子序列 动态规划五步曲: 1.确定dp[i][j]的含义 2.找出递推公式 3.初始化dp数组 4.确定遍历顺序 5.打印dp数组 LeetCode 1035.不相交的线 LeetCode 53.最大子序列和(动态规划) 动态规划五步曲: 1.确定…...

leetcode 541.反转字符串II
⭐️ 题目描述 🌟 leetcode链接:https://leetcode.cn/problems/reverse-string-ii/ ps: 这道题描述的有点晦涩难懂,意思就是每隔k个反转k个,末尾不够k个时全部反转,开始就不够k个也全部反转。 代码&#…...

MyBatis与Spring整合以及AOP和PageHelper分页插件整合
目录 前言 一、MyBatis与Spring整合的好处以及两者之间的关系 1.好处 2.关系 二、MyBatis和Spring集成 1.导入pom.xml 2.编写配置文件 3.利用mybatis逆向工程生成模型层代码 三、常用注解 四、AOP整合pageHelper分页插件 创建一个切面 测试 前言 MyBatis是一个开源的…...

《认知觉醒》读书笔记之潜意识
模糊--人生是一场消除模糊的比赛。 学习知识,消除认知模糊 掌握的工具越多,认知能力越强,消除模糊的能力就越强。 元认知-----》 如何反观自己。 刻意练习----》 如何精进自己。 运动改造大脑---》 如何激化自己的运动热情。 学习知识的…...

Stable Diffusion 系列教程 | 图生图基础
前段时间有一个风靡全网的真人转漫画风格,受到了大家的喜欢 而在SD里,就可以通过图生图来实现类似的效果 当然图生图还有更好玩的应用,我们一点一点来探索 首先我们来简单进行一下图生图的这一个实践---真人转动漫 1. 图生图基本界面 和…...
cuda编程day001
一、环境: ①、linux cuda-11.3 opecv4.8.0 不知道头文件和库文件路径,用命令查找: # find /usr/local -name cuda.h 2>/dev/null # 查询cuda头文件路径 /usr/local/cuda-11.3/targets/x86_64-linux/include/cuda.h # find /usr/…...
Java 中使用 ES 高级客户端库 RestHighLevelClient 清理百万级规模历史数据
🎉工作中遇到这样一个需求场景:由于ES数据库中历史数据过多,占用太多的磁盘空间,需要定期地进行清理,在一定程度上可以释放磁盘空间,减轻磁盘空间压力。 🎈在经过调研之后发现,某服务…...
梯度下降230821a)
C++最易读手撸神经网络两隐藏层(任意Nodes每层)梯度下降230821a
// c神经网络手撸20梯度下降22_230820a.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。 #include<iostream> #include<vector> #include<iomanip> // setprecision #include<sstream> // getline stof() #include<fstream…...

Leetcode 2235.两整数相加
一、两整数相加 给你两个整数 num1 和 num2,返回这两个整数的和。 示例 1: 输入:num1 12, num2 5 输出:17 解释:num1 是 12,num2 是 5 ,它们的和是 12 5 17 ,因此返回 17 。示例…...
Postman —— postman实现参数化
什么时候会用到参数化 比如:一个模块要用多组不同数据进行测试 验证业务的正确性 Login模块:正确的用户名,密码 成功;错误的用户名,正确的密码 失败 postman实现参数化 在实际的接口测试中,部分参数每…...
LeetCode--HOT100题(41)
目录 题目描述:102. 二叉树的层序遍历(中等)题目接口解题思路代码 PS: 题目描述:102. 二叉树的层序遍历(中等) 给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地&am…...
)
微信小程序教学系列(6)
第六章:小程序商业化 第一节:小程序的商业模式 在这一节中,我们将探讨微信小程序的商业模式,让你了解如何将你的小程序变成一个赚钱的机器! 1. 广告收入 小程序的商业模式之一是通过广告收入赚钱。你可以在小程序中…...
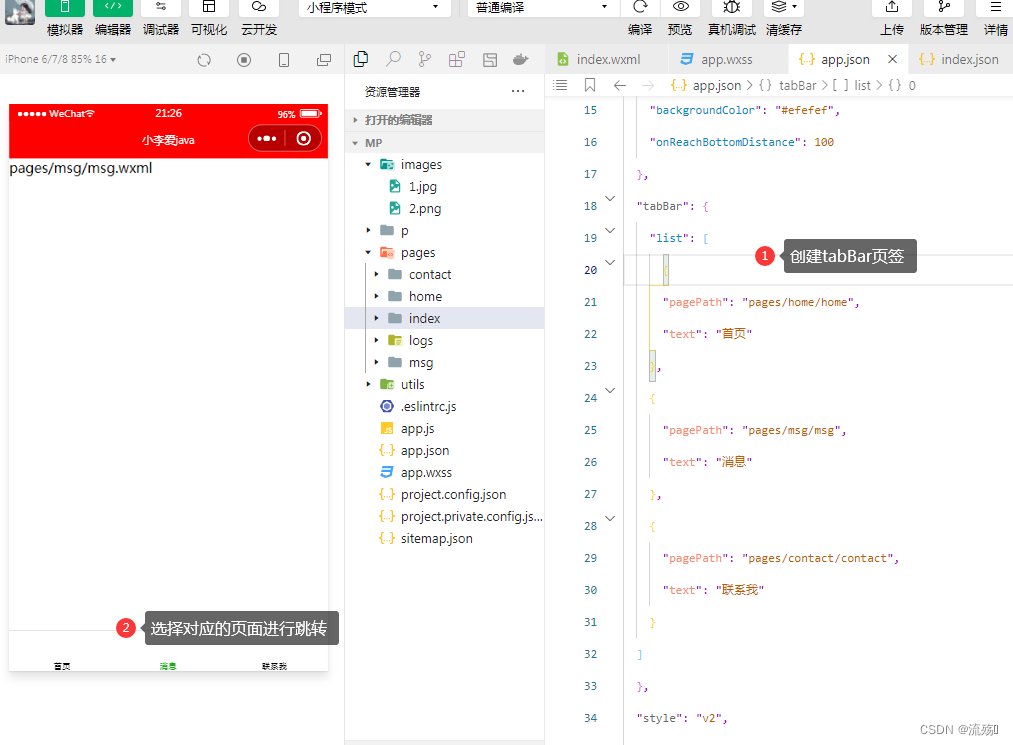
小程序中的全局配置以及常用的配置项(window,tabBar)
全局配置文件和常用的配置项 app.json: pages:是一个数组,用于记录当前小程序所有页面的存放路径,可以通过它来创建页面 window:全局设置小程序窗口的外观(导航栏,背景,页面的主体) tabBar:设置小程序底部的 tabBar效果 style:是否…...
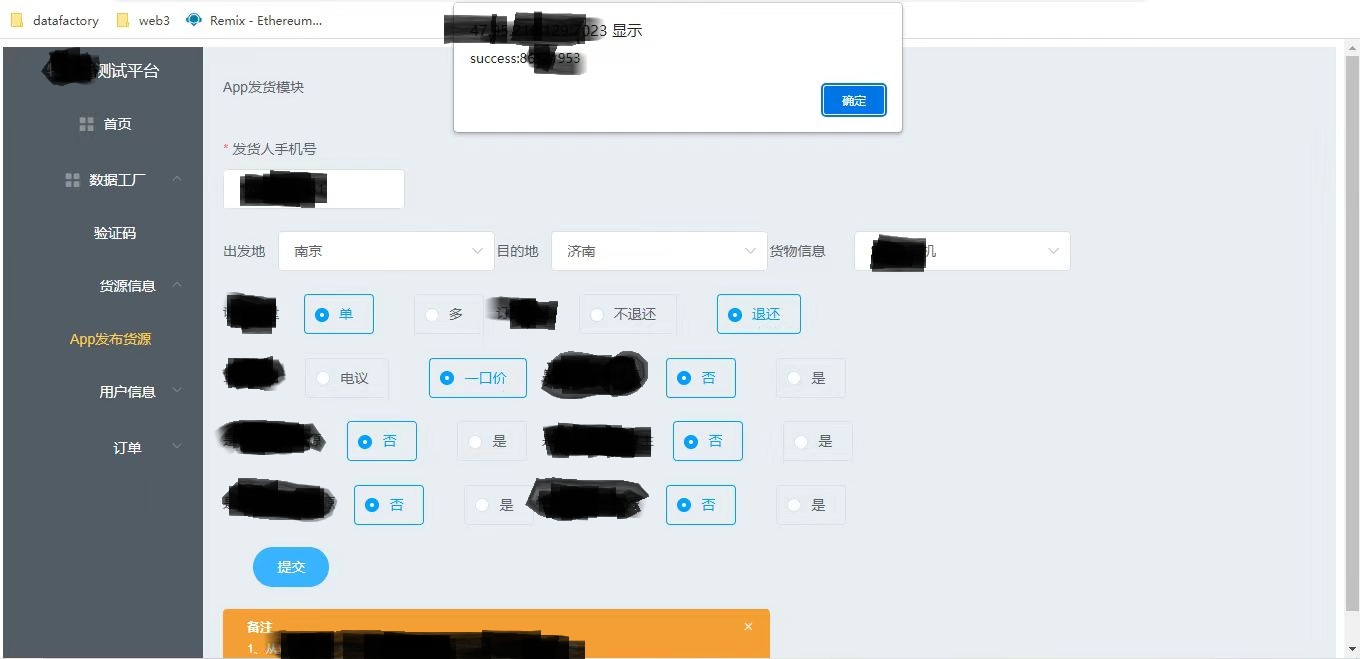
数据工厂调研及结果展示
数据工厂 一、背景 在开发自测、测试迭代测试、产品验收的过程中,都需要各种各样的前置数据,大致分为如下几类: 账号(实名、权益等级、注册等) 货源(优货、急走、相似、一手、普通货源等) …...
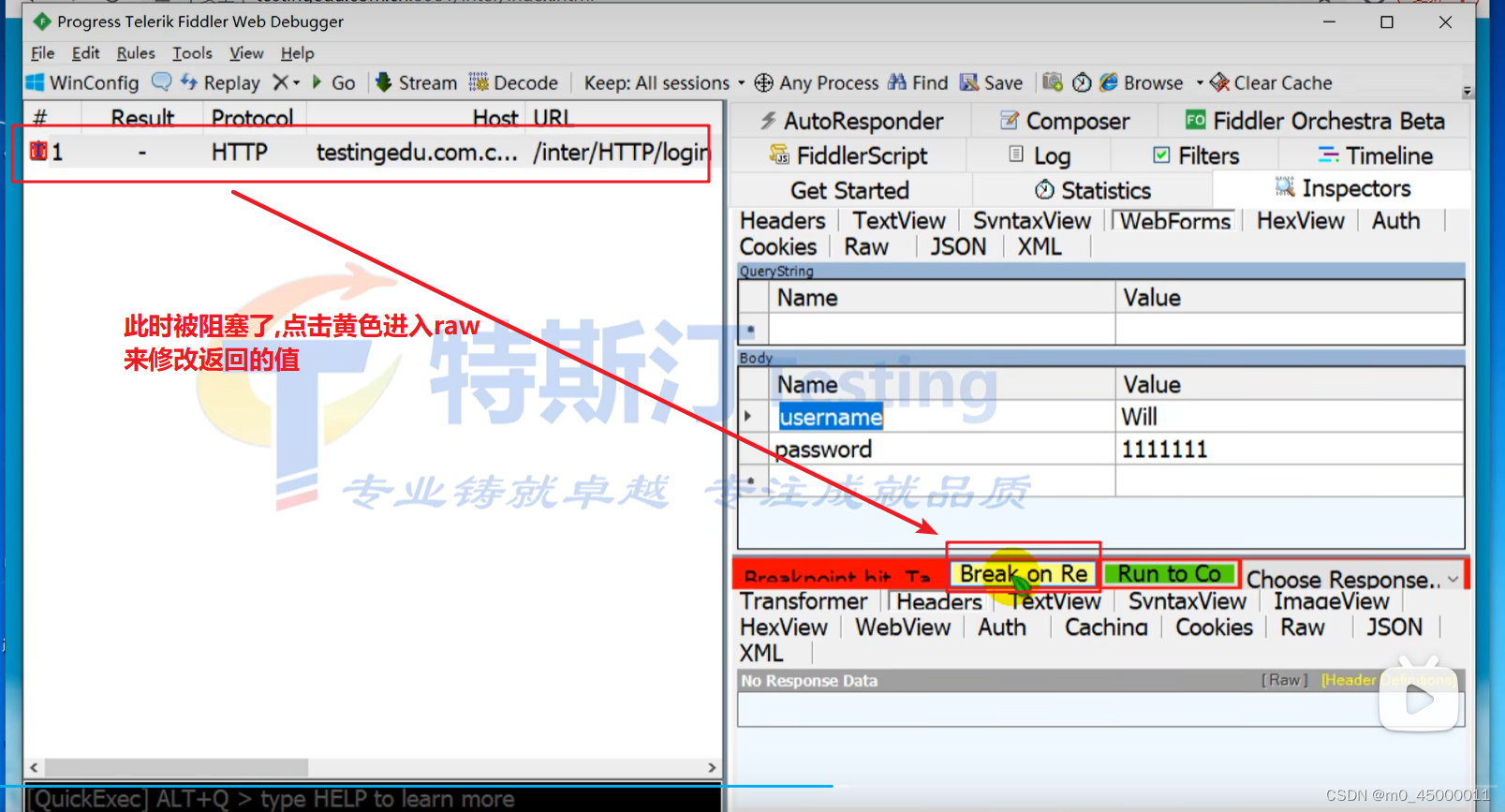
抓包相关,抓包学习
检查网络流量 - 提琴手经典 (telerik.com) Headers Reference - Fiddler Classic (telerik.com) 以上是fiddler官方文档 F12要勾选保留日志 不勾选的话跳转到新页面之前页面的日志不会在下方显示 会保留所有抓到的包 如果重定向到别的页面 F12抓包可能看不到响应信息,但是…...
云原生之使用Docker部署SSCMS内容管理系统
云原生之使用Docker部署SSCMS内容管理系统 一、SSCMS介绍二、本地环境介绍2.1 本地环境规划2.2 本次实践介绍 三、本地环境检查3.1 检查Docker服务状态3.2 检查Docker版本3.3 检查docker compose 版本 四、下载SSCMS镜像五、部署SSCMS内容管理系统5.1 创建SSCMS容器5.2 检查SSC…...

uniapp -- 在组件中拿到pages.json下pages设置navigationBarTitleText这个值?
1:在 pages.json 文件中设置 navigationBarTitleText,例如: {"pages": [{"path": "pages/home/index","style": {"navigationBarTitleText": "首页",&...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
