前缀和差分(C/C++)
目录
1. 前缀和的定义
2. 一维前缀和
2.1 计算公式
2.2 用途
2.3 小试牛刀
3. 二维前缀和
3.1 用途
1. 前缀和的定义
对于一个给定的数列A,他的前缀和数中 S 中 S[ i ] 表示从第一个元素到第 i 个元素的总和。
如下图:绿色区域的和就是前缀和数组中的 S [ 6 ]。
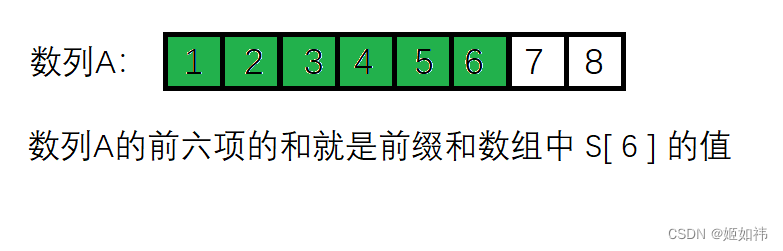
这里你可能就会有一个疑问?为什么是 S[ 6 ] 的位置,而不是 S[ 5 ] 的位置呢??即前缀和组中 S[ 0 ] 并没有参与求和的运算。这里先卖个关子等会在做解释。
2. 一维前缀和
2.1 计算公式
前缀和数组的每一项是可以通过原序列以递推的方式推出来的,递推公式就是:S[ i ] = S[ i - 1 ] + A[ i ]。S[ i - 1 ] 表示前 i - 1 个元素的和,在这基础上加上 A[ i ],就得到了前 i 个元素的和 S [ i ]。
2.2 用途
一维前缀和的主要用途:求一个序列中某一段区间中所有元素的和。有如下例子:
有一个长度为 n 的整数序列。
接下来输入 m 个询问,每个询问输入一对 l,r。
对于每个询问,输出原序列中第 l 个数到第 r 个数的和。
这边是对前缀和的应用,如果用常规的方法:从 l 到 r 遍历一遍,则需要O(N)的时间复杂度。但是有前缀和数组的话,我们可以直接利用公式:sum = S[ r ] - S[ l - 1 ],其中sum是区间中元素的总和,l 和 r 就是区间的边界。下图可帮助理解这个公式。
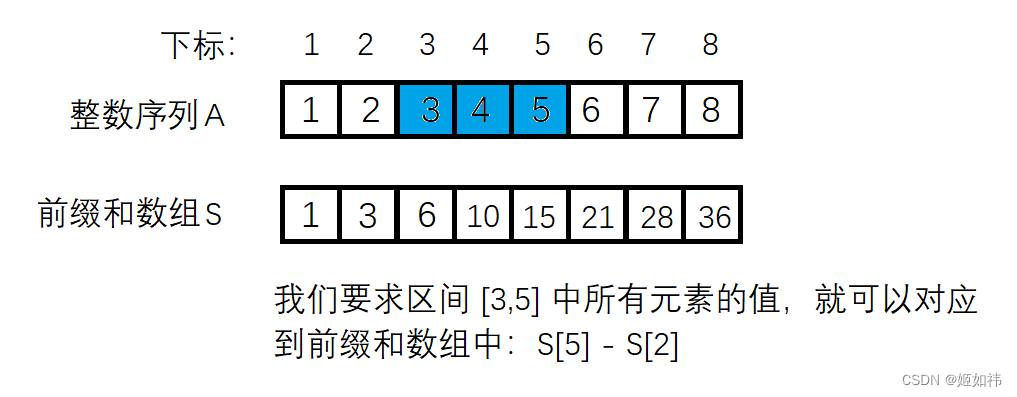
当我们要求的是序列 A 的前 n 个数之和时,如果我们是从下标为 0 的位置开始存储前缀和数组,此公式:sum = S[ r ] - S[ l - 1 ] 显然就无法使用了,为了是这个公式适用于所有情况,我们将从下标为 1 的位置开始存储前缀和,并且将下标为 0 的位置初始化为 0。
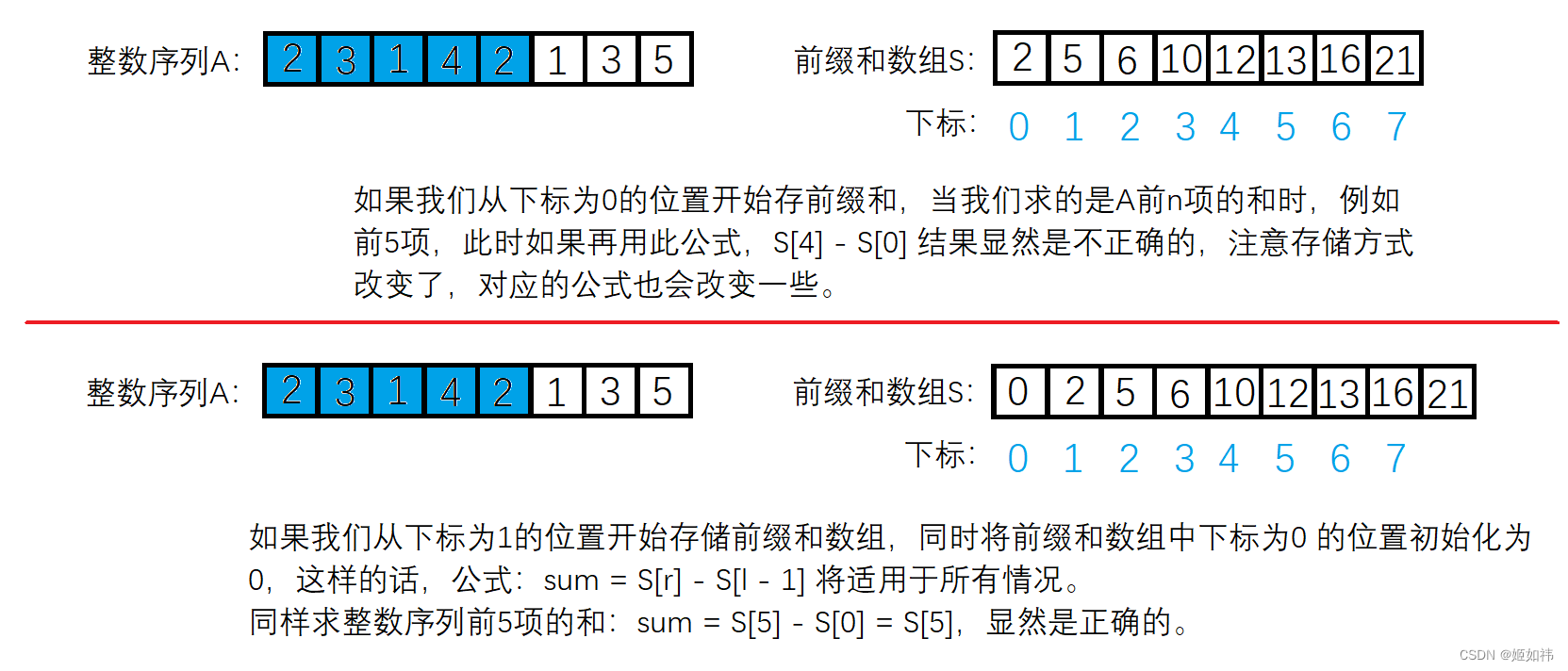
这便是为什么 S[ 0 ] 并未参与求和的运算。
有了上面的分析我们就能轻松解决这道题啦!
有一个长度为 n 的整数序列。
接下来输入 m 个询问,每个询问输入一对 l,r。
对于每个询问,输出原序列中第 l 个数到第 r 个数的和。
输入格式
第一行包含两个整数n和m。
第二行包含n个整数,表示整数数列。
接下来m行,每行包含两个整数l和r,表示一个询问区间的范围。
void test01()
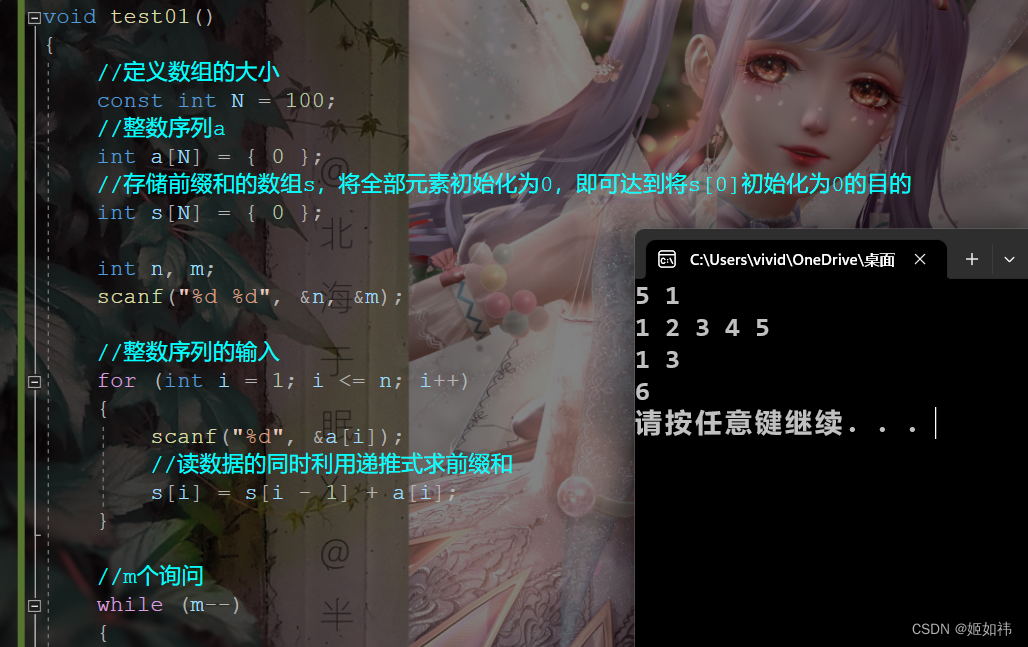
{//定义数组的大小const int N = 100;//整数序列aint a[N] = { 0 };//存储前缀和的数组s,将全部元素初始化为0,即可达到将s[0]初始化为0的目的int s[N] = { 0 };int n, m;scanf("%d %d", &n, &m);//整数序列的输入for (int i = 1; i <= n; i++){scanf("%d", &a[i]);//读数据的同时利用递推式求前缀和s[i] = s[i - 1] + a[i];}//m个询问while (m--){int l, r;scanf("%d %d", &l, &r);//利用求区间元素个数的通式计算结果printf("%d\n", s[r] - s[l - 1]);}}int main()
{//一维前缀和test01();system("pause");return 0;
}
2.3 小试牛刀
原题链接:
209. 长度最小的子数组 - 力扣(LeetCode)
https://leetcode.cn/problems/minimum-size-subarray-sum/
题目描述:
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组,并返回其长度。如果不存在符合条件的子数组,返回 0 。
3. 二维前缀和
和一维前缀和的原理类似,只不过二维前缀和求的是一个矩阵中所有元素的和。
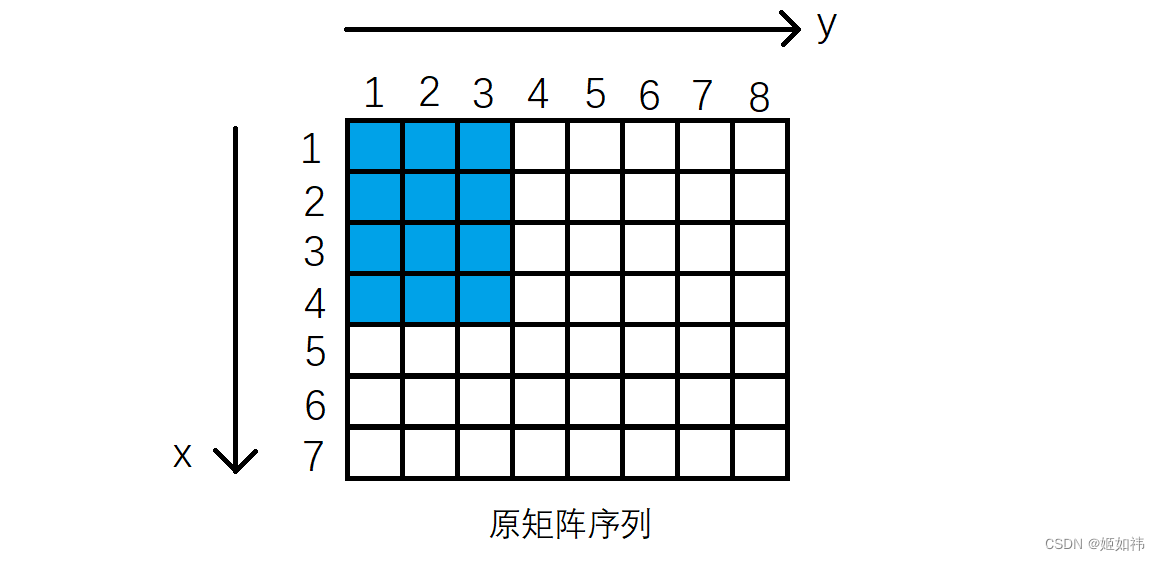
例如:对与 x = 4,y = 3 这么一组输入,就是将原矩阵序列中蓝色区域的元素相加,得到的结果便是前缀和矩阵S中 S[ 4 ][ 3 ] 的值。
3.1 用途
一维前缀和求的是某一个区间中所有元素的和,那么二维前缀和就是求一个大矩阵中某个小的矩阵中所有元素的和。
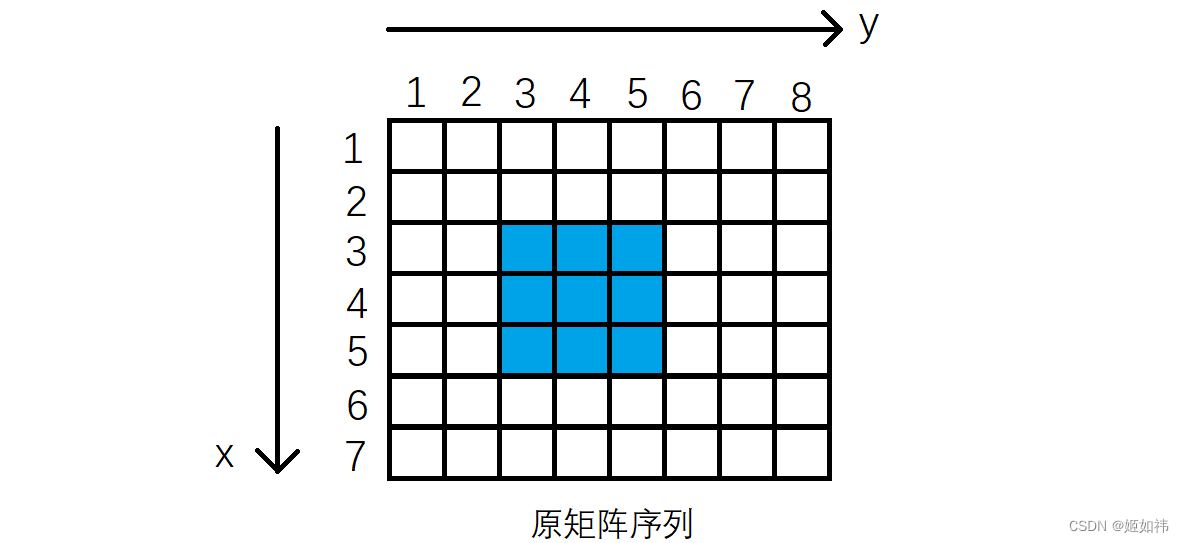
例如上图:我们要求蓝色矩阵中所有元素的和。
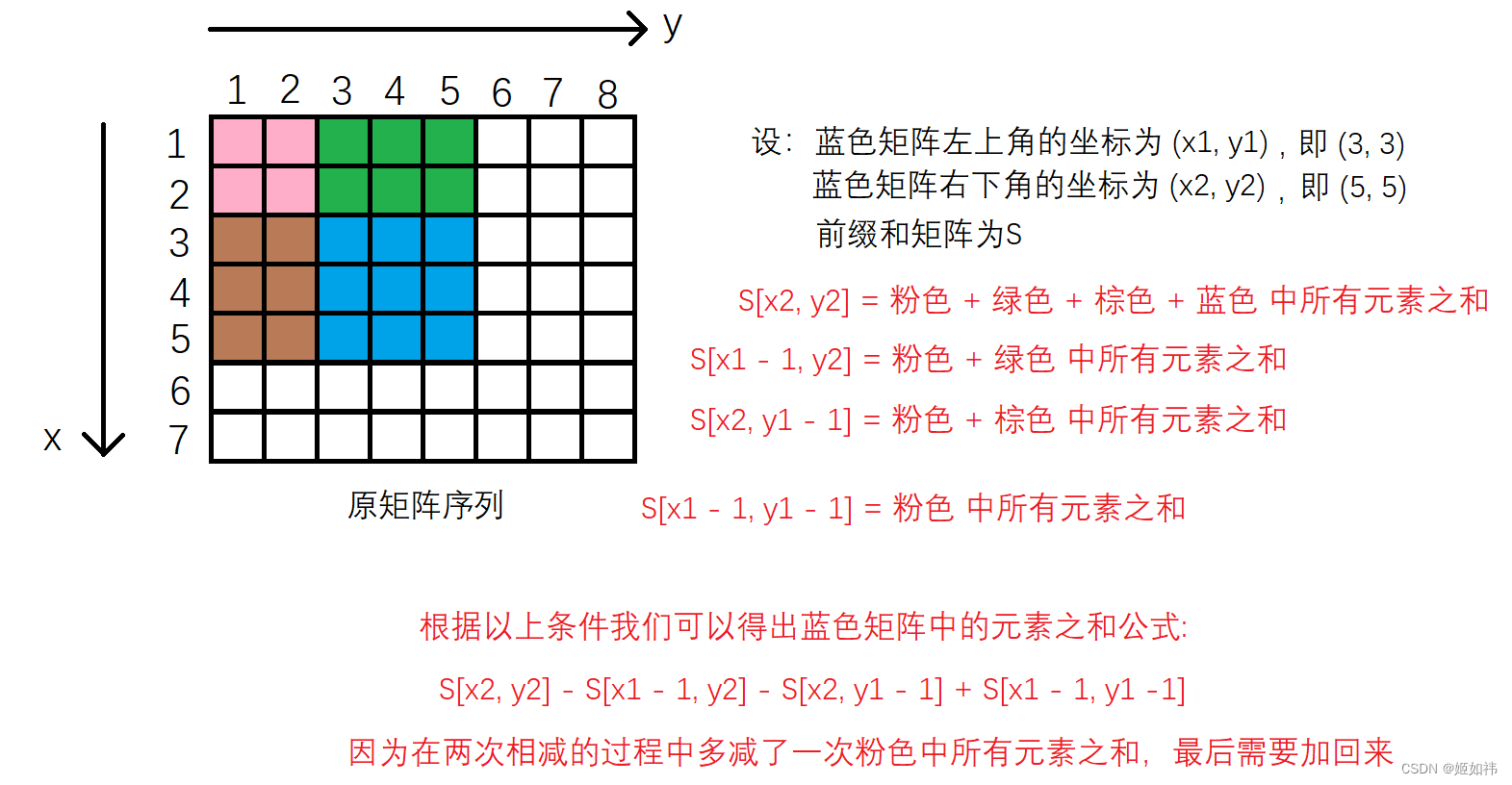
现在就差最后一步了,怎么求出前缀和矩阵中的每一个值嘞??同理利用递推关系求就阔以啦。
S[ i ][ j ] = S[ i - 1 ][ j ] + S[ i ][ j - 1 ] - S[ i - 1][ j - 1 ] + a[ i ][ j ]
其中a为原矩阵序列。可以尝试举一个具体的例子来理解。
有了以上知识,我们可以尝试写代码求一下。
输入一个n行m列的矩阵,在输入q个询问,每个询问包含四个整数x1,y1,x2,y2,表示一个子矩阵左上角的坐标和右下角的坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数n,m,q
接下来n行,每行包含m个整数,表示整数矩阵。
接下来q行,每行包含四个整数x1,y1,x2,y2,表示一组询问。
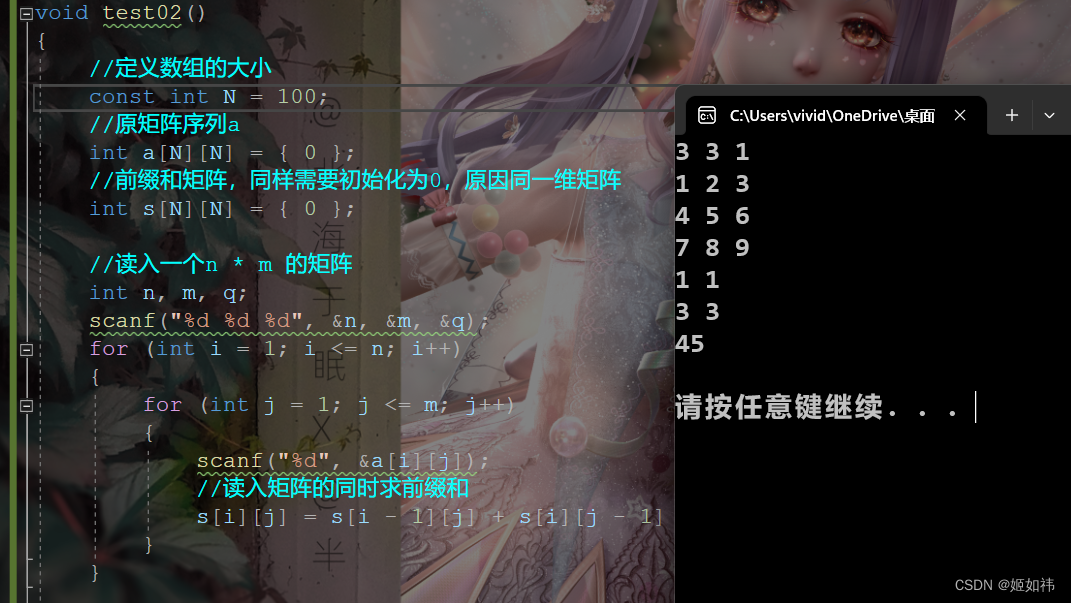
void test02()
{//定义数组的大小const int N = 100;//原矩阵序列aint a[N][N] = { 0 };//前缀和矩阵,同样需要初始化为0,原因同一维矩阵int s[N][N] = { 0 };//读入一个n * m 的矩阵int n, m, q;scanf("%d %d %d", &n, &m, &q);for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){scanf("%d", &a[i][j]);//读入矩阵的同时求前缀和s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];}}//q个询问while (q--){int x1, y1, x2, y2;scanf("%d %d %d %d", &x1, &y1, &x2, &y2);//利用前面推导过的公式直接打印数据即可printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);}printf("\n");
}int main()
{//二维前缀和test02();system("pause");return 0;
} 
相关文章:

前缀和差分(C/C++)
目录 1. 前缀和的定义 2. 一维前缀和 2.1 计算公式 2.2 用途 2.3 小试牛刀 3. 二维前缀和 3.1 用途 1. 前缀和的定义 对于一个给定的数列A,他的前缀和数中 S 中 S[ i ] 表示从第一个元素到第 i 个元素的总和。 如下图:绿色区域的和就是前缀和数组…...

回文子串的数量[寻找回文子串的完整思路过程]
寻找回文子串的完整思路过程前言一、回文串的数量二、动态规划1、完整思考过程2、go总结参考文献前言 回文字符串,就是从左遍历和从右遍历的字符是相同顺序的,转换一下,就是该字符串是对称的。寻找回文子串面临两个直接的问题,1-…...
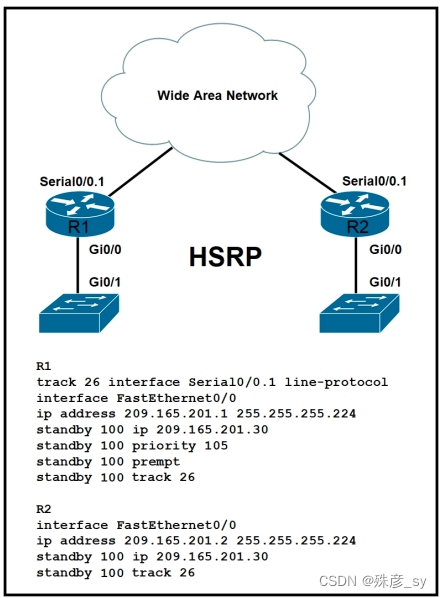
CCNP350-401学习笔记(301-350题)
301、Drag and drop the virtual component from the left onto their descriptions on the right. 302、Which two actions, when applied in the LAN network segment, will facilitate Layer 3 CAPWAP discovery for lightweight AP? (Choose two.)A. Utilize DHCP option …...

【LeetCode】No.225. 用队列实现栈 -- Java Version
题目链接:https://leetcode.cn/problems/implement-stack-using-queues/ 1. 题目介绍(225. 用队列实现栈) 请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、t…...
45个写规范代码的小技巧
目录 1、规范命名 2、规范代码格式 3、写好代码注释 4、try catch 内部代码抽成一个方法 5、方法别太长 6、抽取重复代码 7、多用return 8、if条件表达式不要太复杂 9、优雅地参数校验 10、统一返回值 11、统一异常处理 12、尽量不传递null值 13、尽量不返回null值…...
MindFusion Diagramming for Java, 最新版 Crack
Diagramming for Java, V4.6.1 A unique Java Swing library for any type of flowchart.您需要的每一个图表功能 图表、方案、图形、网络、算法、树、图表 - 所有这些都是使用 MindFusion Diagramming for Java 工具快速轻松地构建的。结果令人着迷。 Java Dagram 库ÿ…...
中间件安全—Apache常见漏洞
中间件安全—Apache常见漏洞1.Apache常见漏洞1.1.Apache介绍1.2.Apache HTTPD 换行解析漏洞(CVE-2017-15715)1.2.1.漏洞介绍1.2.2.漏洞环境1.2.2.1.运行漏洞环境1.2.2.2.访问漏洞环境1.2.3.漏洞复现1.2.3.1.拦截1.2.3.2.添加换行1.2.3.3.访问文件1.3.Apa…...
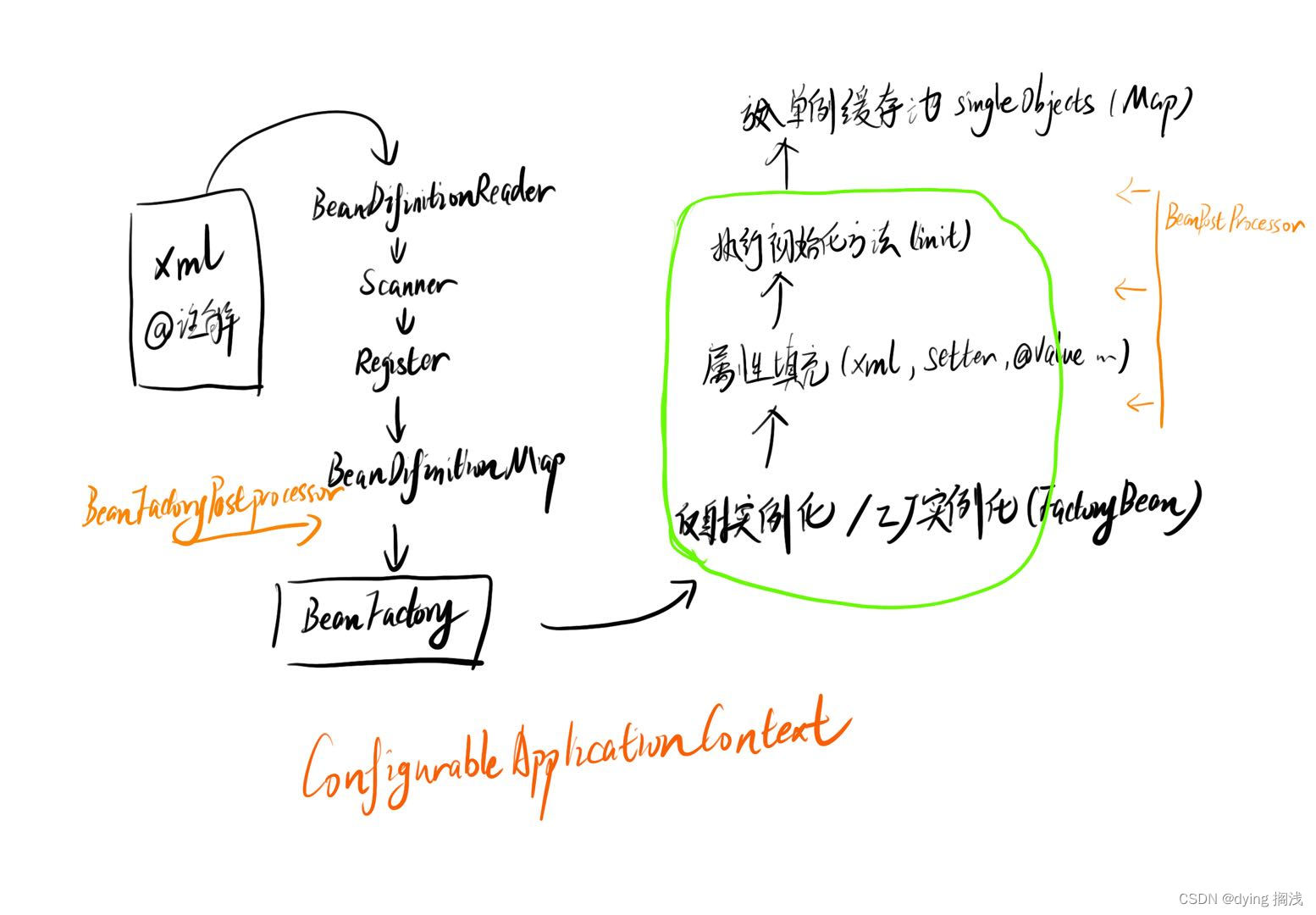
Spring IOC 容器 Bean 加载过程
Spring IOC 容器 Bean 加载过程 Spring 对于我们所有的类对象进行了统一抽象,抽象为 BeanDefinition ,即 Bean 的定义,其中定义了类的全限定类名、加载机制、初始化方式、作用域等信息,用于对我们要自动装配的类进行生成。 Sprin…...
)
【DRF】Django Rest Framework(5.DRF中的通用视图类-GenericAPIView方法说明与使用说明)
1. GenericAPIView [通用视图类],概述 继承自 APIView增加了操作序列化器和数据库查询的方法,作用是为下面Mixin扩展类的执行提供方法支持。通常在使用时,可搭配一个或者多个Mixin扩展类源码 当我们查看 GenericAPIView 的源码时,…...

STM32 OTA应用开发——自制BootLoader
STM32 OTA应用开发——自制BootLoader 目录STM32 OTA应用开发——自制BootLoader前言1 环境搭建2 BootLoader工作原理以及常见分区介绍3 BootLoader的制作4 烧录下载配置5 运行测试结束语前言 什么是OTA? 百度百科:空中下载技术(Over-the-Ai…...

时域和频域的简单理解
目录文章背景结论举例说明说回频域连续或离散总结文章背景 时域和频域在傅里叶变换和拉普拉斯变换,z变换中经常提到的高频词。本文的重点就是想说明怎么理解 “频域” 这个名词。 结论 频域就是一个信号 所有组成频率的取值范围的集合 举例说明 以大家从中小学开…...

华为OD机试 - 第 K 个最小码值的字母 | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 简易压缩算法(Python) | 机试题算法思路 【2023】 华为OD机试题 - 获取最大软件版本号(JavaScript) 华为OD机试 - 猜字谜(Python) | 机试题+算法思路 【2023】 华为OD机试 - 删除指定目录(Python) | 机试题算法思路 【2023】 华为OD机试 …...
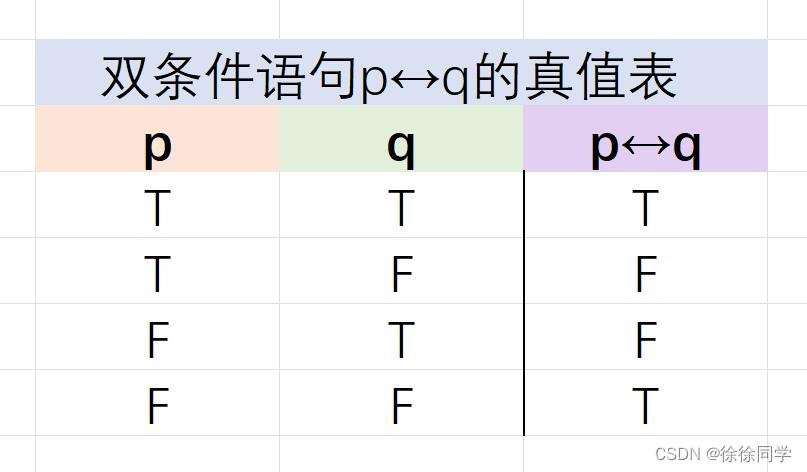
离散数学笔记_第一章:逻辑和证明(1)
1.1命题逻辑1.1.1 命题 1.1.2 逻辑运算符 定义1: 否定联结词定义2: 合取联结词定义3: 析取联结词定义4: 异或联结词1.1.3 条件语句 定义5: 条件语句定义6: 双条件语句1.1.1 命题 1.命题:是…...

Rust FFI 与C语言互相调用
参考 https://cloud.tencent.com/developer/article/2077534 https://github.com/shepmaster/rust-ffi-omnibus cbindgen 简介 二进制方式构建 $ cargo install cbindgen //默认构建C头文件 C语言需要 --lang C $ cd /path/to/my/project && cbindgen . -o target/…...

从全局变量寻找到Tomcat回显方式
前言 对于回显的获取主要是在ApplicationFilterChain类的lastServicedRequest / lastServicedResponse两个属性,是使用的ThreadLocal进行修饰的,并且,在执行请求的过程中,通过反射修改属性值,能够记录下当前线程的req…...

Tapdata Connector 实用指南:数据入仓场景之数据实时同步到 BigQuery
【前言】作为中国的 “Fivetran/Airbyte”, Tapdata 是一个以低延迟数据移动为核心优势构建的现代数据平台,内置 60 数据连接器,拥有稳定的实时采集和传输能力、秒级响应的数据实时计算能力、稳定易用的数据实时服务能力,以及低代码可视化操作…...

关于机器人状态估计(12)-VIO/VSLAM的稀疏与稠密
VIO三相性与世界观室内ALL IN ONE 首先以此链接先对近期工作的视频做个正经的引流,完成得这么好的效果,仅仅是因为知乎限流1分钟以内的视频,导致整个浏览量不到300,让人非常不爽。 这套系统已经完成了,很快将正式发布…...
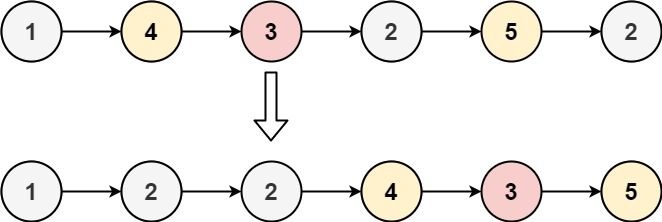
Python每日一练(20230220)
目录 1. 存在重复元素 II 2. 按要求实现程序功能 3. 分割链表 附录 链表 1. 存在重复元素 II 给定一个整数数组和一个整数 k,判断数组中是否存在两个不同的索引 i 和 j,使得 nums [i] nums [j],并且 i 和 j 的差的 绝对值 至多为 k。 …...

技术总监的“技术提升”
技术负责人的能力要求是什么?成本中心技术负责人最重要的工作是让其他CXO理解、认可并且支持技术部的工作,否则作为成本部门,在公司的地位会很低。技术创新光是让其他部门理解还不行,技术还需要创造价值,所以需要做技术创新。上面…...
kettle安装部署_简单认识_Spoon勺子界面---大数据之kettle工作笔记002
然后我们来看一下这个kettle的安装,很简单,下载解压就可以了 上面的地址是官网很烂 下面的地址好一些 这个是官网可以看到很慢,很不友好 这个是下面那个地址,可以看到 最新的是9.0了,一般都用 一般都用8.2 这里下载这个就可以了 下载以后可以看到有个pdi...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
