Unity 之利用 localEulerAngle与EulerAngle 控制物体旋转
文章目录
- 概念讲解
- localEulerAngle与EulerAngle的区别

概念讲解
欧拉角(Euler Angles)是一种常用于描述物体在三维空间中旋转的方法。它使用三个角度来表示旋转,分别绕物体的三个坐标轴(通常是X、Y和Z轴)进行旋转。这种表示方式的优势是直观且易于理解,但也存在一些问题,如万向锁问题。下面是一些关于欧拉角的重要概念:
-
欧拉角的表示方式:
欧拉角通常使用三个角度来表示物体的旋转,分别是绕X轴、Y轴和Z轴的旋转角度。这三个角度可以分别记作 yaw(偏航角)、pitch(俯仰角)和 roll(滚转角)。这些角度可以被用来描述物体相对于其初始方向的旋转。 -
旋转顺序:
欧拉角的旋转顺序非常重要,因为不同的顺序会影响最终的旋转结果。例如,XYZ顺序意味着首先绕X轴旋转,然后绕Y轴,最后绕Z轴。常见的旋转顺序包括XYZ、XZY、YXZ、YZX、ZXY和ZYX等。 -
万向锁问题:
欧拉角表示存在一个问题,称为万向锁问题。在某些情况下,当两个旋转角度非常接近90度时,会导致一个旋转角度失去独立性,从而无法正确表示物体的旋转。这会导致物体的旋转看起来异常,称为万向锁。为了避免这个问题,通常会使用四元数(Quaternion)等其他旋转表示方法。 -
应用领域:
欧拉角常用于游戏开发、计算机图形学和航空航天等领域,因为它们直观且易于人类理解。但在实际编程中,特别是在涉及复杂的旋转和动画计算时,往往更常使用四元数等更稳定的旋转表示方法。
总之,欧拉角是一种描述物体旋转的常用方法,但在实际应用中需要考虑其局限性和可能的问题。在处理旋转时,了解欧拉角及其应用范围,以及什么时候应该使用其他表示方法,是非常重要的。
localEulerAngle与EulerAngle的区别
在Unity中,localEulerAngles 和 eulerAngles 都是用来表示物体旋转的属性,但它们有一些区别。
-
localEulerAngles:- 这个属性表示物体相对于其父物体的本地旋转角度(局部坐标系下的旋转角度)。
- 当你修改物体的
localEulerAngles时,会影响物体的旋转,并将其旋转角度从局部坐标系转化为全局坐标系。
-
eulerAngles:- 这个属性表示物体相对于世界坐标系的旋转角度。
- 当你修改物体的
eulerAngles时,会直接修改物体在全局坐标系下的旋转角度。
主要区别在于这两个属性是基于不同坐标系的。如果你希望在局部坐标系下进行旋转修改,通常会使用 localEulerAngles。如果你希望直接在全局坐标系下进行旋转修改,可以使用 eulerAngles。
这里是一个简单示例,用来说明这两者之间的区别:
using UnityEngine;public class RotateObject : MonoBehaviour
{public float rotationSpeed = 60.0f; // 旋转速度// Update is called once per framevoid Update(){// 使用 localEulerAngles 进行局部坐标系的旋转//获取localEulerAnglesVector3 localRotation = transform.localEulerAngles;//沿着y 轴旋转localRotation.y += rotationSpeed * Time.deltaTime;transform.localEulerAngles = localRotation;// 使用 eulerAngles 进行全局坐标系的旋转//获取eulerAnglesVector3 globalRotation = transform.eulerAngles;globalRotation.y += rotationSpeed * Time.deltaTime;transform.eulerAngles = globalRotation;}
}
在上述示例中,localEulerAngles 和 eulerAngles 都被用来实现旋转,一个是基于局部坐标系,另一个是基于全局坐标系。你可以根据需求选择合适的属性来控制旋转。
相关文章:

Unity 之利用 localEulerAngle与EulerAngle 控制物体旋转
文章目录 概念讲解localEulerAngle与EulerAngle的区别 概念讲解 欧拉角(Euler Angles)是一种常用于描述物体在三维空间中旋转的方法。它使用三个角度来表示旋转,分别绕物体的三个坐标轴(通常是X、Y和Z轴)进行旋转。这…...
)
从零学算法 (剑指 Offer 13)
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如&am…...

854之数据结构
一.线性表 1.顺序表 #include <iostream> #include<stdlib.h> using namespace std; #define max 100 typedef struct {int element[max];int last; } List; typedef int position ; void Insert(int x, position p, List &L) {position q;if (L.last > ma…...
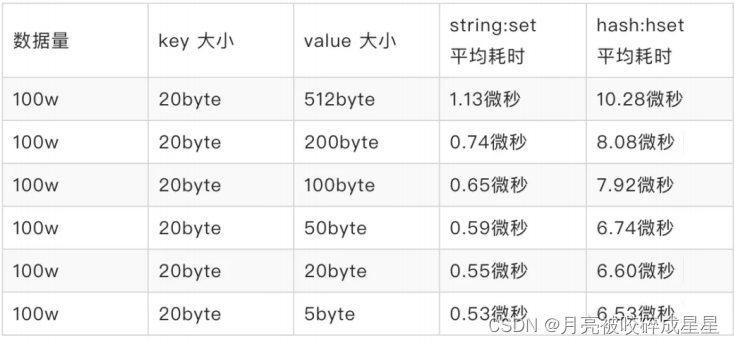
Redis从基础到进阶篇(二)----内存模型与内存优化
目录 一、缓存通识 1.1 ⽆处不在的缓存 1.2 多级缓存 (重点) 二、Redis简介 2.1 什么是Redis 2.2 Redis的应用场景 三、Redis数据存储的细节 3.1 Redis数据类型 3.2 内存结构 3.3 内存分配器 3.4 redisObject 3.4.1 type 3.4.2 encoding 3…...
DBO优化SVM的电力负荷预测,附MATLAB代码
今天为大家带来一期基于DBO-SVM的电力负荷预测。 原理详解 文章对支持向量机(SVM)的两个参数进行优化,分别是:惩罚系数c和 gamma。 其中,惩罚系数c表示对误差的宽容度。c越高,说明越不能容忍出现误差,容易过拟合。c越小࿰…...

第一百二十五回 dart中List和Map的常见用法
文章目录 概念介绍使用方法初始化相互转换元素操作 经验分享 我们在上一章回中介绍了Flexible组件相关的内容,本章回中将介绍 dart中的List和Map.闲话休提,让我们一起Talk Flutter吧。 概念介绍 我们在这里介绍的List也叫列表,它表示一组相…...
小白到运维工程师自学之路 第七十九集 (基于Jenkins自动打包并部署Tomcat环境)2
紧接上文 4、新建Maven项目 clean package -Dmaven.test.skiptrue 用于构建项目并跳过执行测试 拉到最后选择构建后操作 SSH server webExec command scp 192.168.77.18:/root/.jenkins/workspace/probe/psi-probe-web/target/probe.war /usr/local/tomcat/webapps/ /usr/loca…...
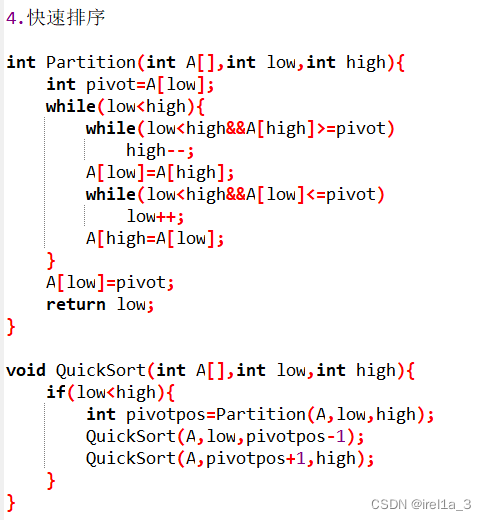
林【2021】
三、应用 1.字符串abaaabaabaa,用KMP改进算法求出next和nextval的值 2.三元组矩阵 4.二叉树变森林 四、代码(单链表递增排序,二叉树查找x,快速排序)...
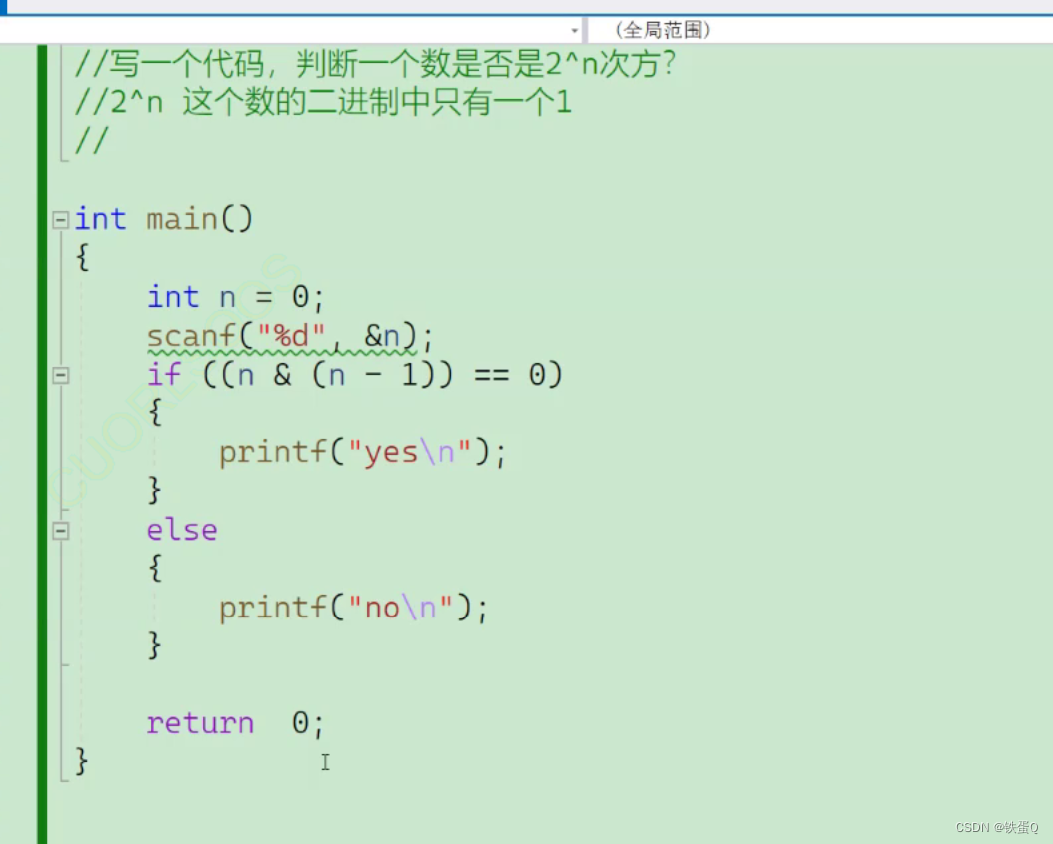
c语言练习题30:判断一个数是否为2^n
判断一个数是否为2^n 思路:2^n中只有一个1故可以通过n&(n-1)是否为0来判断。 代码:...

VX小程序 实现区域转图片预览
图例 方法一 1、安装插件 wxml2canvas npm install --save wxml2canvas git地址参照:https://github.com/wg-front/wxml2canvas 2、类型 // 小程序页面 let data{list:[{type:wxml,class:.test_center .draw_canvas,limit:.test_center,x:0,y:0}] } 3、数据结…...
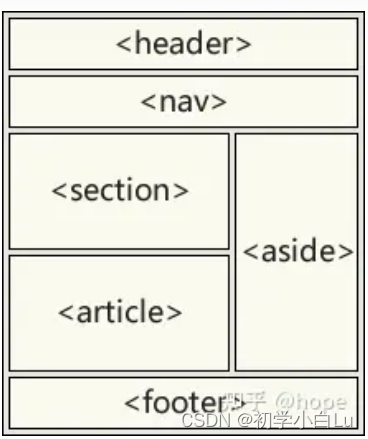
HTML5-1-标签及属性
文章目录 语法规范标签规范标签列表通用属性基本布局 页面的组成: HTML(HyperText Markup Language,超文本标记语言)是用来描述网页的一种语言,它不是一种编程语言,而是一种标记语言。 HTML5 是下一代 HTM…...

5017. 垦田计划
Powered by:NEFU AB-IN Link 文章目录 5017. 垦田计划题意思路代码 5017. 垦田计划 题意 略 思路 二分最小需要几天即可 注意: 天数不能低于k二分时,若耗时天数小于mid,直接continue 代码 /* * Author: NEFU AB-IN * Date: 2023-08-26 22:4…...

【校招VIP】产品思维分析之面试新的功能点设计
考点介绍: 这种题型是面试里出现频度最高,也是难度最大的一种,需要面试者对产品本身的功能、扩展性以及行业都有一定的了解。而且分析时间较短,需要一定的产品能力和回答技巧。 『产品思维分析之面试新的功能点设计』相关题目及解…...

indexDB vue 创建数据库 创建表 添加对象数据
1 .open(dbName,1) 版本号可以省略 let dbName hist-data-1dconst request indexedDB.open(dbName); // 如果你不知道数据库的版本号,可以省略第二个参数,这样 indexedDB 会默认为你打开最新版本的数据库,因为版本号总是自增长的 2 第一次…...
Django基础1——项目实现流程
文章目录 一、前提了解二、准备开发环境2.1 创建项目2.1.1 pycharm创建2.1.2 命令创建 2.2 创建应用 例1:效果实现例2:网页展示日志文件 一、前提了解 基本了解: 官网Django是Python的一个主流Web框架,提供一站式解决方案…...

基于SSM的在线购物系统——LW模板
摘 要 人类进入21世纪以来,很多技术对社会产生了重大的影响。信息技术是最具代表的新时代技术,信息技术起源于上世纪,在起初的时候只是实现在单机上进行信息的数字化管理,随着网络技术、软件开发技术、通讯技术的发展,…...

Mac操作系统上设置和配置PPPoE连接
嗨,在使用Mac的小伙伴么!你是否在Mac操作系统上尝试设置和配置PPPoE连接,却不知道怎么设置?别担心,今天我将为你一步步教你如何在Mac上进行设置和配置。无论你是新手还是有经验的用户,本文都将帮助你轻松完…...

Python类的属性和方法
Python类是一种面向对象编程的基本概念,它可以用来创建对象,对象可以拥有属性和方法。 属性是类的特征,它们用于存储对象的状态。属性可以是任何数据类型,例如整数、字符串、列表等。在类中,属性通常定义为类的变量&am…...

C#Queue<T>队列出现弹出元素被最后一次压入得元素覆盖的问题
问题代码: //以下为现有代码的大概描述,只可意会,不可执行!!!Queue<Move> mQueue new Queue<Move>(); //该接口为下面描述线程A、线程B调用的接口 private void ActionTrigger(Move move)//M…...

python3GUI--模仿一些b站网页端组件By:PyQt5(详细介绍、附下载地址)
文章目录 一.前言二.展示1.banner1.静图2.动图 2.一般视频组件1.静图2.动图 3.排行榜1.静图2.动图 三.设计心得(顺序由简到难)1.排行榜2.一般视频组件3.banner 四.总结五.下载地址 一.前言 播客二连发&…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
