Day45|leetcode 70. 爬楼梯、322. 零钱兑换、279.完全平方数
leetcode 70. 爬楼梯
题目链接:70. 爬楼梯 - 力扣(LeetCode)
本题可以用背包问题来解决,就相当于楼顶是背包,台阶是物品,相当于之前写法的进阶版。
代码实现
class Solution {
public:int climbStairs(int n) {vector<int> dp(n + 1,0);dp[0] = 1;for(int i = 1;i <= n;i++) {for(int j = 1;j <= 2;j++) {if(i - j >= 0) dp[i] += dp[i - j];}}return dp[n];}
};leetcode 322. 零钱兑换
题目链接:322. 零钱兑换 - 力扣(LeetCode)
视频链接:动态规划之完全背包,装满背包最少的物品件数是多少?| LeetCode:322.零钱兑换_哔哩哔哩_bilibili
题目概述
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins =[1, 2, 5], amount =11输出:3解释:11 = 5 + 5 + 1
示例 2:
输入:coins =[2], amount =3输出:-1
示例 3:
输入:coins = [1], amount = 0 输出:0
思路
1.确定dp数组含义:dp[j]:凑足总额为j所需钱币的最少个数为dp[j]。
2.确定递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j])。
3.数组初始化:dp[0]=0,非0下标初始化成最大值。(以前都是max,这次是min)
4.确定遍历顺序:本题不用强调顺序,本题既不是组合数也不是排列数,第一层遍历物品和背包哪个都行,第二层也是。
5.打印dp数组:
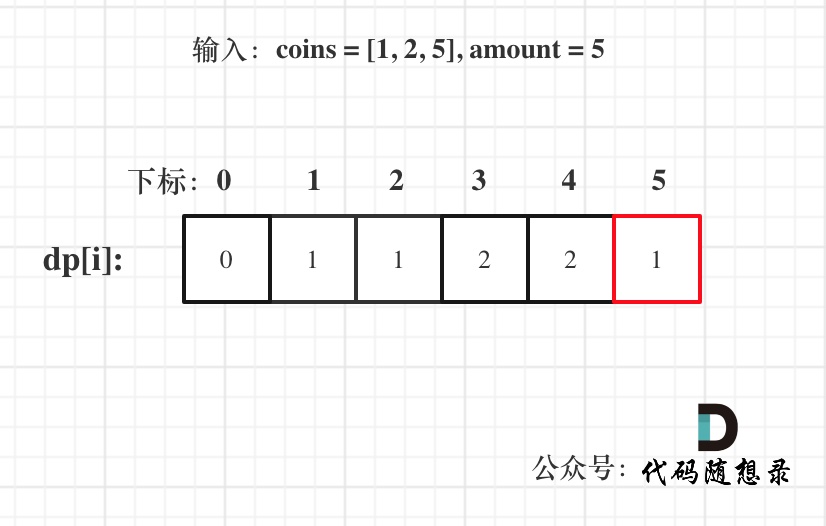
代码实现(先物品后背包)
class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount + 1, INT_MAX);dp[0] = 0;for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包if (dp[j - coins[i]] != INT_MAX) { // 如果dp[j - coins[i]]是初始值则跳过dp[j] = min(dp[j - coins[i]] + 1, dp[j]);}}}if (dp[amount] == INT_MAX) return -1;return dp[amount];}
};代码实现(先背包后物品)
class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount + 1, INT_MAX);dp[0] = 0;for (int i = 1; i <= amount; i++) { // 遍历背包for (int j = 0; j < coins.size(); j++) { // 遍历物品if (i - coins[j] >= 0 && dp[i - coins[j]] != INT_MAX ) {dp[i] = min(dp[i - coins[j]] + 1, dp[i]);}}}if (dp[amount] == INT_MAX) return -1;return dp[amount];}
};leetcode 279.完全平方数
题目链接:279. 完全平方数 - 力扣(LeetCode)
视频链接:动态规划之完全背包,换汤不换药!| LeetCode:279.完全平方数_哔哩哔哩_bilibili
题目概述
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n =12输出:3 解释:12 = 4 + 4 + 4
示例 2:
输入:n =13输出:2 解释:13 = 4 + 9
本题和上一道题其实都差不多,换汤不换药的的东西。
代码实现(先物品后背包)
class Solution {
public:int numSquares(int n) {vector<int> dp(n + 1,INT_MAX);dp[0] = 0;for(int i = 1;i * i <= n;i++) {for(int j = i * i;j <= n;j++) {dp[j] = min(dp[j - i * i] + 1,dp[j]);}}return dp[n];}
};代码实现(先背包后物品)
class Solution {
public:int numSquares(int n) {vector<int> dp(n + 1, INT_MAX);dp[0] = 0;for (int i = 0; i <= n; i++) { // 遍历背包for (int j = 1; j * j <= i; j++) { // 遍历物品dp[i] = min(dp[i - j * j] + 1, dp[i]);}}return dp[n];}
};相关文章:

Day45|leetcode 70. 爬楼梯、322. 零钱兑换、279.完全平方数
leetcode 70. 爬楼梯 题目链接:70. 爬楼梯 - 力扣(LeetCode) 本题可以用背包问题来解决,就相当于楼顶是背包,台阶是物品,相当于之前写法的进阶版。 代码实现 class Solution { public:int climbStairs(in…...
arm:day9
1。思维导图 2..I2C实验,检测温度和湿度 iic.h #ifndef __IIC_H__ #define __IIC_H__ #include "stm32mp1xx_gpio.h" #include "stm32mp1xx_rcc.h" #include "gpio.h" /* 通过程序模拟实现I2C总线的时序和协议* GPIOF ---> AHB4…...

【大模型AIGC系列课程 1-2】创建并部署自己的ChatGPT机器人
OpenAI API 调用 获取 openai api api-key https://platform.openai.com/account/api-keys 利用 python requests 请求 openai 参考 openai 接口说明:https://platform.openai.com/docs/api-reference/chat/create import json # 导入json包 import requests # 导入req…...
启动metastore服务报错
启动Metastore的时候报错: 简略的报错信息: MetaException(message:Error creating transactional connection factory)Caused by: MetaException(message:Error creating transactional connection factory)Caused by: javax.jdo.JDOFatalInternalExce…...

c 语言 算法 技巧 之 用移位来代替乘除
除法 当你需要计算一个数的一半时,通常我们会考虑使用除法运算(/)来实现。然而,计算机内部的运算中,除法通常比加法和乘法运算慢得多,因为除法需要更多的处理步骤。 位运算在这种情况下可以提供一个快速的…...

python爬虫实战零基础(3)——某云音乐
爬取某些云网页音乐,无需app 分析网页第二种方式批量爬取 声明:仅供参考学习,参考,若有不足,欢迎指正 你是不是遇到过这种情况,在pc端上音乐无法下载,必须下载客户端才能下载? 那么&…...
渗透测试漏洞原理之---【XSS 跨站脚本攻击】
文章目录 1、跨站 脚本攻击1.1、漏洞描述1.2、漏洞原理1.3、漏洞危害1.4、漏洞验证1.5、漏洞分类1.5.1、反射性XSS1.5.2、存储型XSS1.5.3、DOM型XSS 2、XSS攻防2.1、XSS构造2.1.1、利用<>2.1.2、JavaScript伪协议2.1.3、时间响应 2.2、XSS变形方式2.2.1、大小写转换2.2.2…...

【浮点数二分】
数的三次方根 #include<iostream> using namespace std;double n;int main(){cin>>n;double l -10000;double r 10000;while((r-l)>1e-8){double mid (lr)/2;if((mid*mid*mid)>n) r mid;else l mid;}printf("%lf",l);return 0; }...
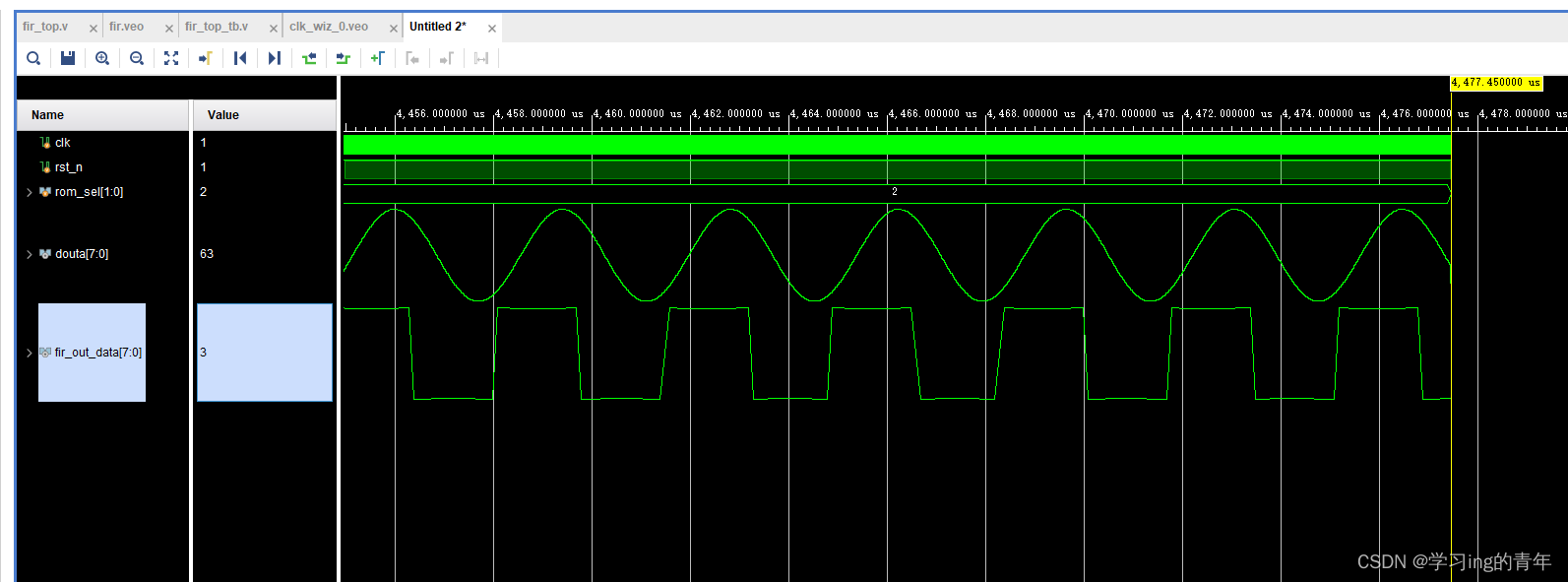
基于FPGA的FIR低通滤波器实现(附工程源码),matlab+vivado19.2+simulation
基于FPGA的FIR低通滤波器实现(附工程源码) 文章目录 基于FPGA的FIR低通滤波器实现(附工程源码)前言一、matlab设计FIR滤波器,生成正弦波1.设计FIR滤波器1.生成正弦波.coe 二、vivado1.fir滤波器IP核2.正弦波生成IP核3.时钟IP核设置4.顶层文件/测试文件代码 三.simul…...
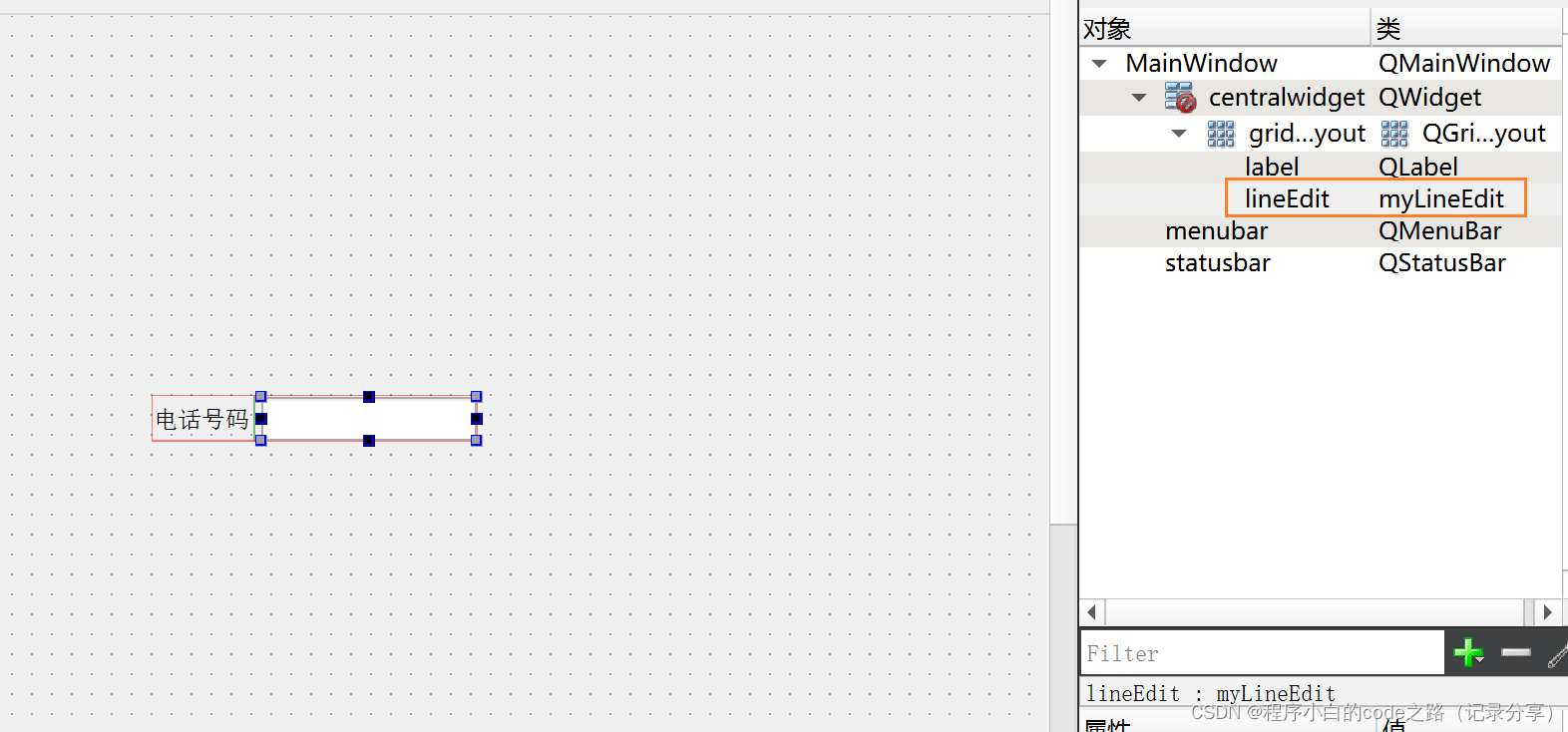
c++ qt--事件(第六部分)
c qt–事件(第六部分) 一.编辑伙伴,编辑顺序(按TAB进行切换) 1.编辑伙伴 此功能在设计界面如下的位置 1.设置伙伴关系 鼠标左键长按一个Label组件然后把鼠标移到另一个组件上 2.伙伴关系的作用 伙伴关系的作用就是…...
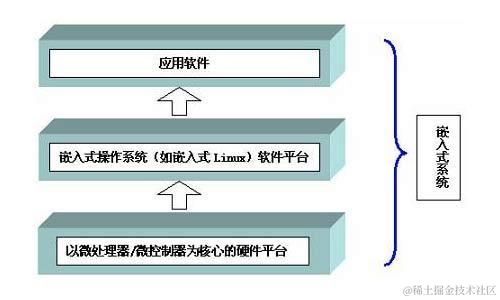
嵌入式系统入门实战:探索基本概念和应用领域
嵌入式系统是一种专用的计算机系统,它是为了满足特定任务而设计的。这些系统通常具有较低的硬件资源(如处理器速度、内存容量和存储容量),但具有较高的可靠性和实时性。嵌入式系统广泛应用于各种领域,如家用电器、汽车、工业控制、医疗设备等。 嵌入式系统的基本概念 微控…...

关于hive sql进行调优的理解
这是一个面试经常面的问题,很不幸,在没有准备的时候,我面到了这个题目,反思了下,将这部分的内容进行总结,给大家一点分享。 hive其实是基于hadoop的数据库管理工具,底层是基于MapReduce实现的&a…...

十大排序算法
一、冒泡排序 冒泡排序(Bubble Sort)是一种简单直观的排序算法。它重复地走访要排序的数列,一次比 较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经…...

PIP 常用操作汇总
1. 升级 python -m pip install --upgrade pip2. 列出所有安装包 pip list3. 查找特定包 pip list | findstr xxx4. 查看特定包 pip show xxx5. 安装软件包 pip install pyzmq24.0.16. 卸载软件包 pip uninstall -y pyzmq7. 查看配置 # 生效的配置(global -&…...

线性代数的本质笔记(3B1B课程)
文章目录 前言向量矩阵行列式线性方程非方阵点积叉积基变换特征向量与特征值抽象向量空间 前言 最近在复习线代,李永乐的基础课我刷了一下,感觉讲的不够透彻,和我当年学线代的感觉一样,就是不够形象。 比如,行列式为…...

快速掌握MQ消息中间件rabbitmq
快速掌握MQ消息中间件rabbitmq 目录概述需求: 设计思路实现思路分析1.video 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy,skip hardness,make a better result,wait for change,c…...

Git push拦截
遇到的问题 今天想提交代码到gitee,结果发现被拦截了,有段提示“forbidden by xxxx”… 我记得xxxx好像是公司的一个防泄密的东西… 这个东西是怎么实现的呢? 解决 原来git提供很多hook,push命令就有一个pre-push的hook&#x…...
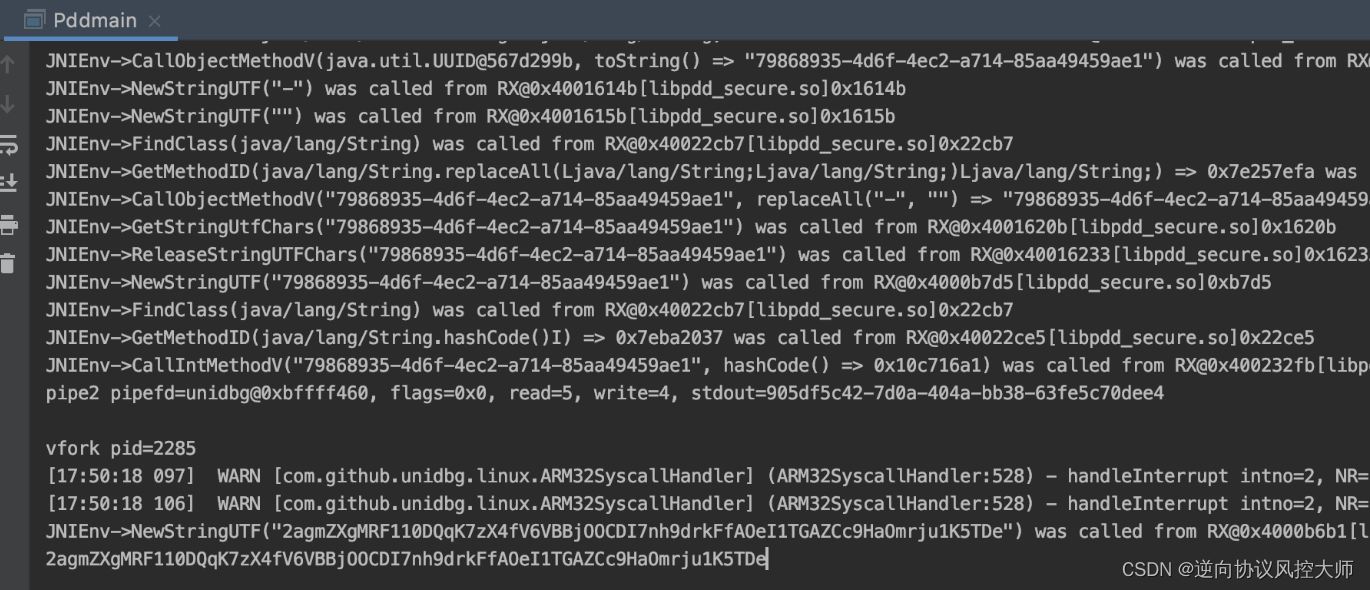
拼多多anti-token分析
前言:拼多多charles抓包分析发现跟商品相关的请求头里都带了一个anti-token的字段且每次都不一样,那么下面的操作就从分析anti-token开始了 1.jadx反编译直接搜索 选中跟http相关的类对这个方法进行打印堆栈 结合堆栈方法调用的情况找到具体anti-token是由拦截器类f…...
基于微信小程序的中医体质辨识文体活动的设计与实现(Java+spring boot+MySQL)
获取源码或者论文请私信博主 演示视频: 基于微信小程序的中医体质辨识文体活动的设计与实现(Javaspring bootMySQL) 使用技术: 前端:html css javascript jQuery ajax thymeleaf 微信小程序 后端:Java s…...
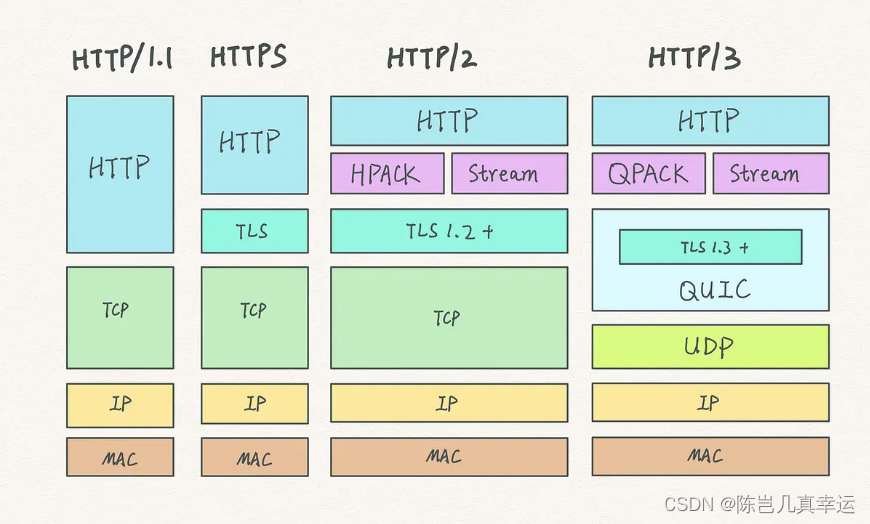
4.16 TCP 协议有什么缺陷?
目录 升级 TCP 的工作很困难 TCP 建立连接的延迟 TCP 存在队头阻塞问题 网络迁移需要重新建立 TCP 连接 升级 TCP 的工作很困难;TCP 建立连接的延迟;TCP 存在队头阻塞问题;网络迁移需要重新建立 TCP 连接; 升级 TCP 的工作很…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...
