数学建模:熵权法
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛
熵权法
- 构建原始矩阵 D a t a Data Data 形状为 m ∗ n m *n m∗n ,其中 m m m 为评价对象, n n n 为评价指标。
- 对 D a t a Data Data矩阵的指标进行正向化处理,得到矩阵 X X X.
- 计算每一个指标在每一个对象下的所占该指标的比重,然后我们便得到了变异值矩阵: P P P
p i j = Y y ¨ ∑ i = 1 m Y i j , i = 1 , ⋯ , m , j = 1 , ⋯ , n \begin{aligned}p_{ij}=\frac{Y_{\ddot{y}}}{\sum_{i=1}^m Y_{ij}},i=1,\cdots,m,j=1,\cdots,n\end{aligned} pij=∑i=1mYijYy¨,i=1,⋯,m,j=1,⋯,n
- 求各指标的信息熵 E E E:
E j = − ln ( m ) − 1 ∑ i = 1 m p i j ln p i j E_j=-\ln(m)^{-1}\sum_{i=1}^mp_{ij}\ln p_{ij} Ej=−ln(m)−1i=1∑mpijlnpij
- 通过信息熵计算各个指标的权重 W W W :其中 k k k 是指标的个数,即 k = n k = n k=n
w j = 1 − E j k − Σ E j ( j = 1 , 2 , … , n ) w_j=\dfrac{1-E_j}{k-\Sigma E_j}(j=1,2,\ldots,n) wj=k−ΣEj1−Ej(j=1,2,…,n)
- 也可以通过计算信息冗余度来计算权重 W W W(本代码采取这种方法):
D j = 1 − E j w j = D j ∑ j = 1 m D j \begin{aligned}D_j&=1-E_j\\\\w_j&=\frac{D_j}{\sum_{j=1}^mD_j}\end{aligned} Djwj=1−Ej=∑j=1mDjDj
- 计算每一个对象的最终得分:
Z i = ∑ j = 1 n X i j W j , i ∈ ( 1 , 2 , 3 , . . . m ) Z_{i}\mathrm{=}\sum_{j=1}^{n}X_{ij}W_{j},i\in(1,2,3, ... m) Zi=j=1∑nXijWj,i∈(1,2,3,...m)
代码实现
function [Score,W]=mfunc_entropyMethod(data)% 熵权法:求解每个指标的权重% paramts: % data: 原始数据矩阵,(m,n) m为评价对象,n为评价指标% returns:% Score:每个评价对象的综合得分% W: 所有指标的权重%数据标准化到0.002-1区间data2=mapminmax(data',0.002,1);data2=data2';%得到信息熵[m,n]=size(data2); % m个对象,n个指标p=zeros(m,n);for j=1:n% 计算第j列的每一列指标在该指标中所占的比例p(:,j)=data2(:,j)/sum(data2(:,j));end for j=1:n% 计算每个指标的信息熵E(j)=-1/log(m)*sum(p(:,j).*log(p(:,j)));end%计算权重W=(1-E)/sum(1-E); % 通过信息冗余度计算%计算得分s=data2*W';Score=100*s/max(s);
end
相关文章:

数学建模:熵权法
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 熵权法 构建原始矩阵 D a t a Data Data 形状为 m ∗ n m *n m∗n ,其中 m m m 为评价对象, n n n 为评价指标。对 D a t a Data Data矩阵的指标进行正向化处理,得到…...
软件测试实训系统建设方案
一 、系统概述 软件测试实训系统是软件开发过程中的一项重要测试活动,旨在验证不同软件模块或组件之间的集成与交互是否正常。综合测试确保各个模块按照设计要求正确地协同工作,以实现整个软件系统的功能和性能。以下是软件测试实训系统的一般流程和步骤…...
部署 ssm 项目到云服务器上(购买云服务器 + 操作远程云服务器 + 服务器中的环境搭建 + 部署项目到服务器)
部署 Web 项目 1、获取 Linux 环境1.1、如何去买一个云服务器1.2、远程操作云服务器1.3、在 Linux 系统中搭建 Java Web 的运行环境。1)安装 JDK(使用包管理器 yum 来安装)2) 安装Tomcat3)安装 MySQL。 1.4、在云服务器…...

python爬虫-使用selenium自动登录微博
环境准备:anaconda、pycharm编辑器、chromedriver(记得下载) 首先查看本地anaconda的python环境和selenium版本号(不同版本的api接口可能不同) conda list python输出 # Name Version Build Channel ipython …...

Python 面试:可变类型和不可变类型作为函数参数,关键字参数
1. 可变类型作为参数 可变对象: list/set/dict 参数会指向可变对象的副本的地址,每次修改的是同一个对象。 def flist(l):l.append(0)print(l)ll [] flist(ll) flist(ll)输出为: [0] [0, 0] # 注意:l只是ll的一个副本,修改l不…...

Web3.0时代什么时候到来,Web3.0有什么机会?
🏆作者简介,黑夜开发者,CSDN领军人物,全栈领域优质创作者✌,CSDN博客专家,阿里云社区专家博主,2023年6月CSDN上海赛道top4。 🏆数年电商行业从业经验,历任核心研发工程师…...

vue心得
不是专业的前端开发,但因为E2E开发和架构设计的需要,必须对前端框架有一些了解。这两年项目前端在用vue,就记录一下vue的使用心得。 心得 component component: vue组件,可在其中完成界面呈现(V…...
JavaScript—数据类型、对象与构造方法
js是什么? JavaScript(简称“JS”) 是一种具有函数优先的轻量级,解释型或即时编译型的编程语言。JavaScript 基于原型编程、多范式的动态脚本语言,并且支持面向对象、命令式、声明式、函数式编程范式。 js有哪些特点呢…...
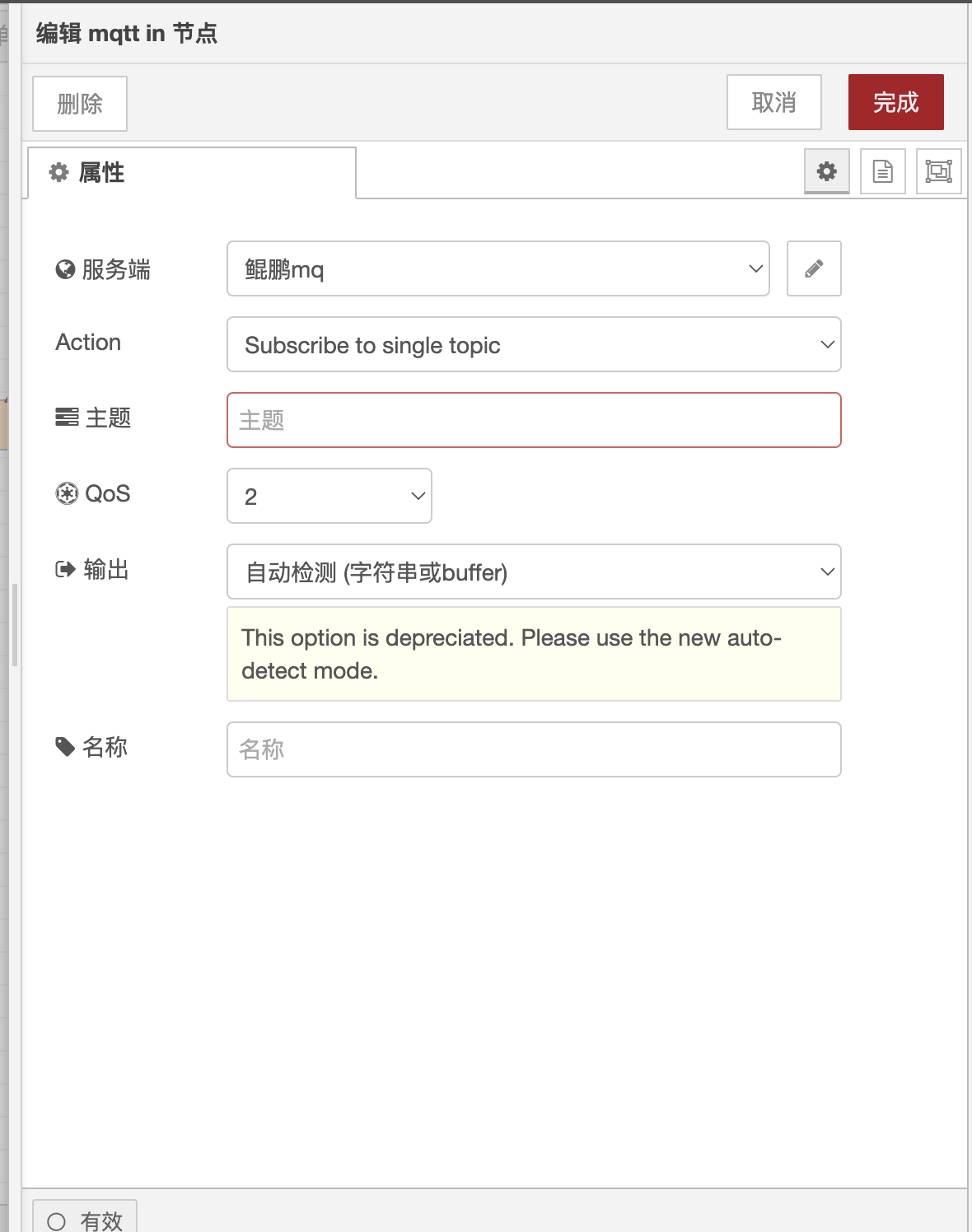
自定义node-red节点中,如何编写节点的配置信息弹窗
前言 最近有读者通过博客向我咨询,在自定义node-red节点时,如何编写该节点的配置页面,就是我们通常见到的,双节节点打开的信息弹窗。如下图: 上面两张图,展示了inject节点与mqtt in 节点的配置弹窗。 在弹窗中,除了上面的删除,取消,完成,和下面的失效按钮。 中间…...
数据之美:探索数据可视化设计的奇妙世界
在信息时代的浪潮中,海量的数据正在影响着我们的生活和决策。然而,数据本身虽然有力量,但如何将其有机地呈现给我们,却成为了一个挑战。数据可视化设计应运而生,它不仅让枯燥的数字变得生动,还带来了一场视…...

docker初始化
避免僵尸进程 使用dump-init FROM node:16 AS builderRUN apt install dumb-init... ...ENTRYPOINT ["/usr/bin/dumb-init", "--"] CMD ["node", "dist/main"]使用tini docker run --init .......开启docker内部ssh docker exec -…...

【C语言】结构体变量引用的一个例子
文件test_funcs.c: #include <stdio.h> #include <stdlib.h>struct t_Test {int n1;int n2; };struct t_Test *alloc_Test(void) {struct t_Test *pTestNULL;pTestmalloc(sizeof(struct t_Test));pTest->n1 1;return pTest; }void func1(struct t_…...

美团笔试题之合并 K 个升序链表
文章目录 题目详情分析暴力求解两两合并链表 Java完整实现代码总结 题目详情 23 美团笔试真题 给你一个链表数组,每个链表都已经按升序排列。 请你将所有链表合并到一个升序链表中,返回合并后的链表。 分析 暴力求解 将所有数值存入一个数组ÿ…...
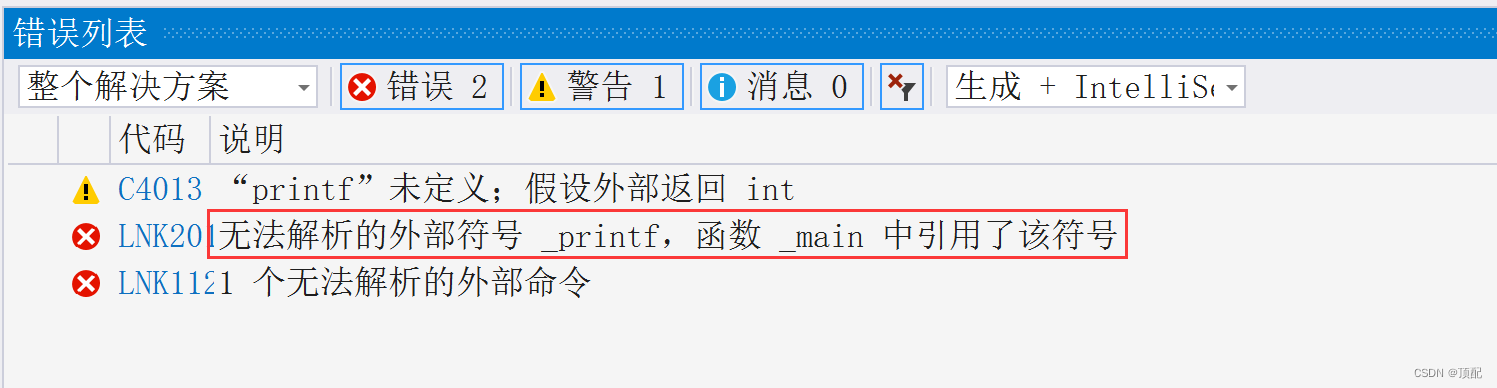
C语言(第三十一天)
6. 调试举例1 求1!2!3!4!...10!的和,请看下面的代码: #include <stdio.h> //写一个代码求n的阶乘 int main() {int n 0;scanf("%d", &n);int i 1;int ret 1;for(i1; i<n; i){ret * i;}printf("%d\n", ret);return …...

【C/C++】虚析构 | 抽象类
创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 🔥c系列专栏:C/C零基础到精通 🔥 给大…...

MySQL 的隐式转换导致诡异现象的案例一则
正是因为 MySQL 对字符串进行隐式转换时会截断再转,而不是像 Oracle、SQL Server 这些数据库针对这种问题直接报错,所以才出现了这个诡异的问题。 作者:刘晨 网名 bisal ,具有十年以上的应用运维工作经验,目前主要从事…...

【考研数学】概率论与数理统计 —— 第二章 | 一维随机变量及其分布(2,常见随机变量及其分布 | 随机变量函数的分布)
文章目录 引言三、常见的随机变量及其分布3.1 常见的离散型随机变量及其分布律(一)(0-1)分布(二)二项分布(三)泊松分布(四)几何分布(五࿰…...
【2023中国算力大会】《中国综合算力指数(2023年)》出炉,宁夏“资源环境”位列全国第1,“算力”跃入Top10
2023年8月18日-19日,2023中国算力大会在宁夏银川举行,本届大会以“算领新产业潮流 力赋高质量发展”为主题,打造“主题论坛、成果展示、产业推介、先锋引领”四大核心内容,全面展示算力产业发展最新成果,为产业各方搭建…...

自动设置服务器全教程
亲爱的爬虫探险家!在网络爬虫的世界里,自动设置代理服务器是一个非常有用的技巧。今天,作为一家代理服务器供应商,我将为你呈上一份轻松实用的教程,帮助你轻松搞定爬虫自动设置代理服务器。 一、为什么需要自动设置代…...
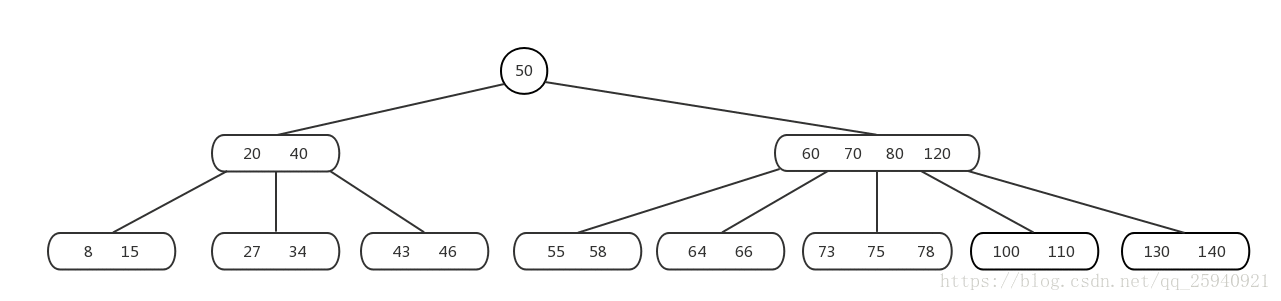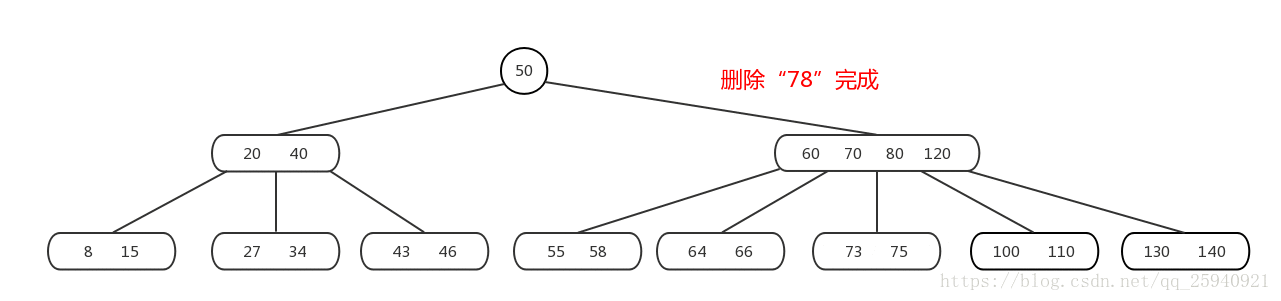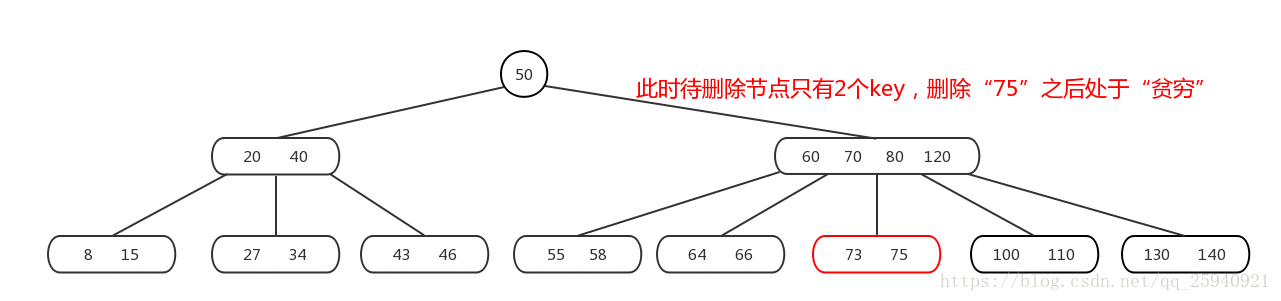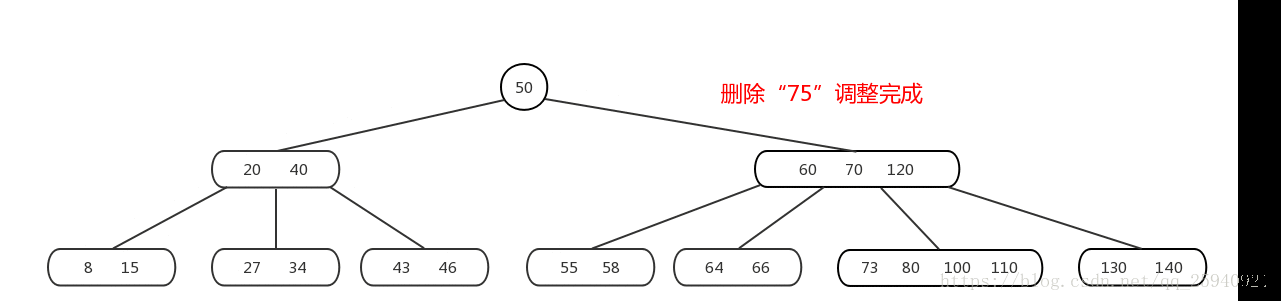
Mysql--技术文档--B树-数据结构的认知
阿丹解读: B树(B tree)和B树(B-tree)都是常见的自平衡搜索树数据结构,用于在存储和检索大量数据时提供高效的操作。 基本概念-B树/B树 B树(B-tree)和B树(B tree&#x…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
