Three.js实现模型,模型材质可拖拽效果 DragControls
Three.js提供了一个拖拽的API DragControls 用于实现模型材质拖拽效果
DragControls:是一个用于在Three.js中实现拖拽控制的辅助类。它简化了在Three.js中实现拖拽物体的过程。
DragControls的构造函数接受三个参数:
objects:一个包含需要进行拖拽的物体的数组。
camera:相机对象,用于将屏幕坐标转换为三维空间坐标。
domElement:渲染器的DOM元素,用于监听鼠标事件。
DragControls实例提供了以下方法和事件:
addEventListener(type, listener):添加事件监听器。支持的事件类型包括’dragstart’、‘drag’和’dragend’。
removeEventListener(type, listener):移除事件监听器。
dispose():释放DragControls实例,清除事件监听器。
DragControls实例还会自动处理鼠标事件,并触发相应的事件。当用户开始拖拽物体时,会触发’dragstart’事件;当物体正在被拖拽时,会触发’drag’事件;当用户停止拖拽物体时,会触发’dragend’事件。
在事件监听器中,可以通过event.object获取被拖拽的物体,通过event.position获取物体在拖拽过程中的位置
注意:DragControls 支持拖拽的材质类型为 type =“Mesh” ,其他类型的材质可能没实际效果
在上一篇 Three.js加载外部glb,fbx,gltf,obj 模型文件 的文章基础上新增一个 setModelMeshDrag(设置模型材质可拖拽方法)
引入拖拽API DragControls
import { DragControls } from 'three/examples/jsm/controls/DragControls';
// 模型材质可拖拽setModelMeshDrag() {const modelMaterialList= []// 获取到需要拖拽的模型材质this.model.traverse((v) => {if (v.isMesh && v.material && v.type=="Mesh") {modelMaterialList.push(v) }})// 创建拖拽实列this.dragControls = new DragControls(this.modelMaterialList, this.camera, this.renderer.domElement);// 拖拽事件监听this.dragControls.addEventListener('dragstart', () => {// 设置控制器不可操作this.controls.enabled = false})this.dragControls.addEventListener('dragend', () => {this.controls.enabled = true})}
完整的代码可参考:https://gitee.com/ZHANG_6666/Three.js3D/blob/master/src/views/renderModel.js
界面效果
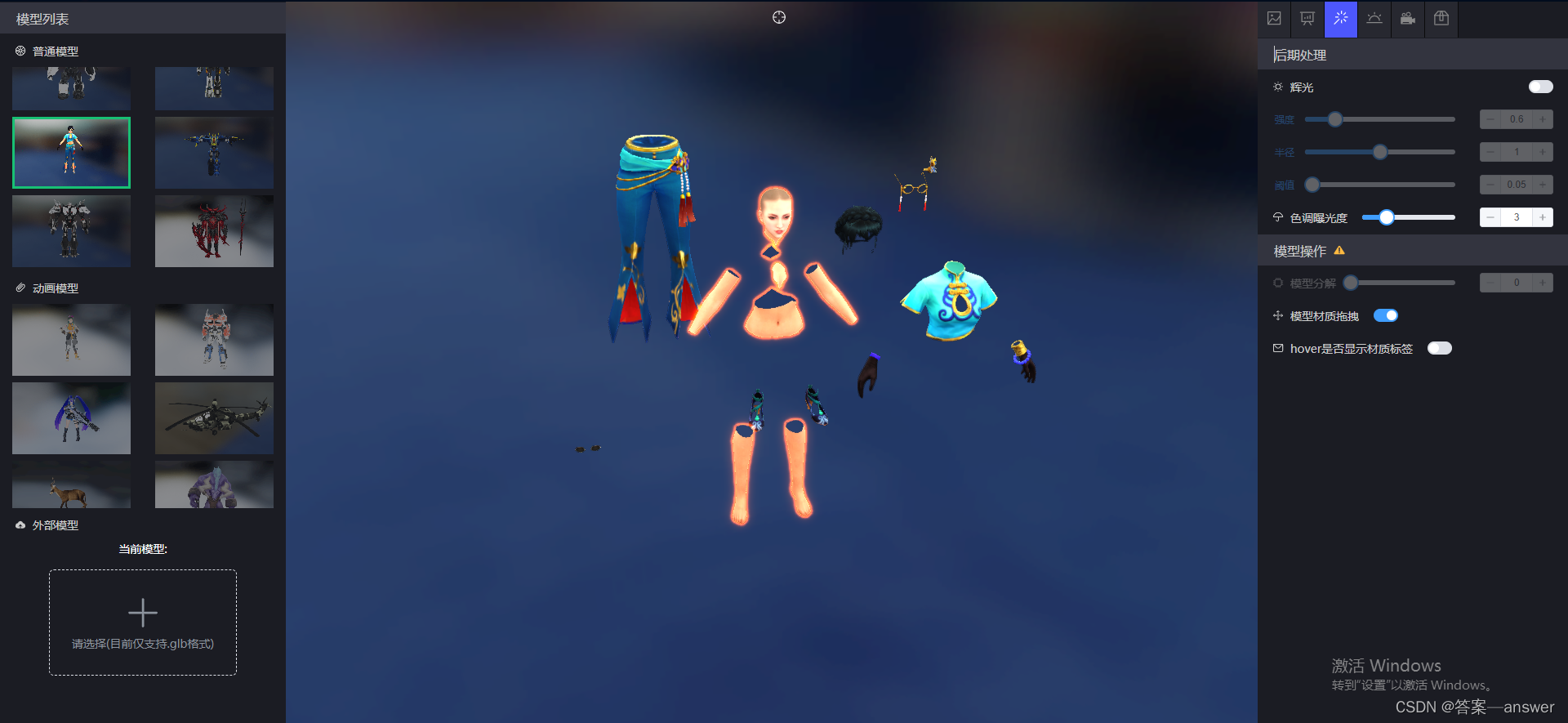
相关文章:

Three.js实现模型,模型材质可拖拽效果 DragControls
Three.js提供了一个拖拽的API DragControls 用于实现模型材质拖拽效果 DragControls:是一个用于在Three.js中实现拖拽控制的辅助类。它简化了在Three.js中实现拖拽物体的过程。 DragControls的构造函数接受三个参数: objects:一个包含需要…...
牛顿法与正则化)
机器学习笔记之优化算法(二十)牛顿法与正则化
机器学习笔记之优化算法——再回首:牛顿法与正则化 引言回顾:经典牛顿法及其弊端牛顿法:算法步骤迭代过程中可能出现的问题正则化 Hessian Matrix \text{Hessian Matrix} Hessian Matrix与相应问题 引言 本节我们介绍经典牛顿法在训练神经网络过程中的迭…...

【Go 基础篇】深入探索:Go语言中的切片遍历与注意事项
嗨,Go语言学习者!在我们的编程旅程中,切片(Slice)是一个极其重要的工具。它可以帮助我们处理各种类型的数据,从而让我们的代码更加灵活和高效。本文将围绕Go语言中切片的遍历方法以及在遍历时需要注意的事项…...

一些经典的SQL语句
查sql中as的用法搜索到的一些经典的sql语句 convert(2008-11-20 18:03:50) In:等值连接,用来查找多表相同字段的记录 Not In:非等值连接,用来查找不存在的记录 Inner join:内连接,主要用来查找都符合条件的记录 Left join:左连接ÿ…...

〔018〕Stable Diffusion 之 批量替换人脸 篇
✨ 目录 🎈 下载插件🎈 插件基础使用🎈 基础使用效果🎈 批量处理图片🎈 多人脸部替换 🎈 下载插件 如果重绘图片的时候,你只想更换人物面部的话,可以参考这篇文章扩展地址ÿ…...

Unity字符串性能问题
前言 分享一些通过书籍和网络学到的知识 每次动态创建一个string,C#都会在堆内存分配一个内存用来分配字符串,因为C#没有对字符串的缓存机制,会导致每次连接、切割、组合的时候都会申请新的内存,并且抛弃原来的内存,等…...

深入浅出SSD:固态存储核心技术、原理与实战(文末赠书)
名字:阿玥的小东东 学习:Python、C/C 主页链接:阿玥的小东东的博客_CSDN博客-python&&c高级知识,过年必备,C/C知识讲解领域博主 目录 内容简介 作者简介 使用Python做一个计算器 本期赠书 近年来国家大力支持半导体行业࿰…...

关于layui+php,三级联动-编辑回显的问题。
注 忍不住吐槽一波。都什么年代了。现在都前后端分离,但是公司老项目非得用tplayui。。 代码如下 layui.use([form], function () {var form layui.form;//php代码渲染页面的时候,将一级分类id和二级分类id带过来,存到页面input框中&#x…...
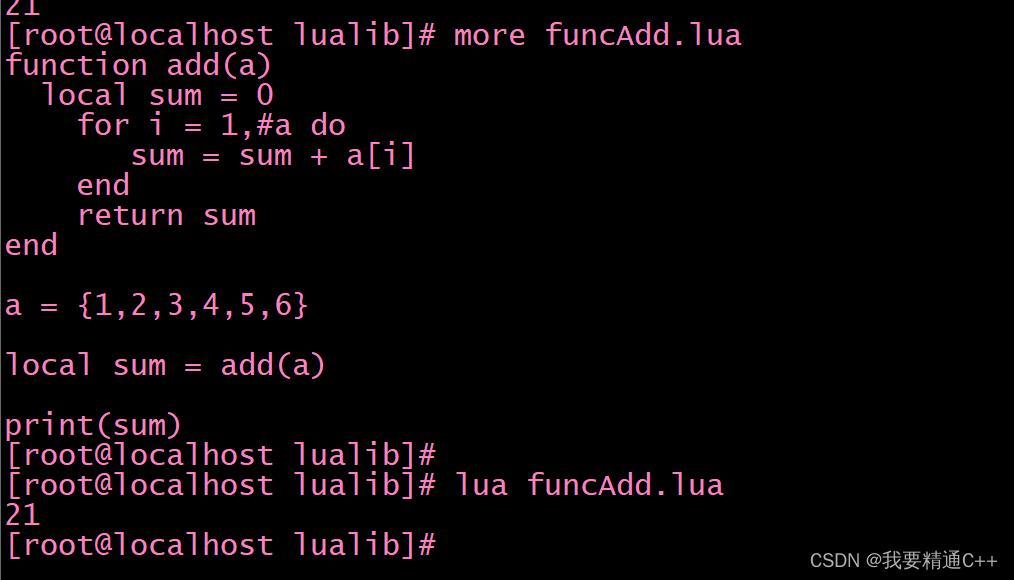
lua的函数
1.一个示例实现列表的元素的求和 [root]# more funcAdd.lua function add(a)local sum 0for i 1,#a dosum sum a[i]endreturn sum enda {1,2,3,4,5,6}local sum add(a)print(sum)...

pytorch/tensorflow 直接给张量中的某个位置的值赋值,操作不可导。
问题:给一个tensor A中[i,j],赋值p。直接操作A[i,j]p可能会导致值覆盖,操作不可导。 解决方案:通过引入一个额外的mask实现。 mask[i,j] 0 mask tf.convert_to_tensor(mask, dtypetf.float32) A (A * mask) (p * (1-mask))p…...

如何使用CSS实现一个平滑滚动到页面顶部的效果(回到顶部按钮)?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 平滑滚动到页面顶部的效果(回到顶部按钮)⭐ 创建HTML结构⭐ 编写CSS样式⭐ 编写JavaScript函数⭐ 添加滚动事件监听器⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右…...
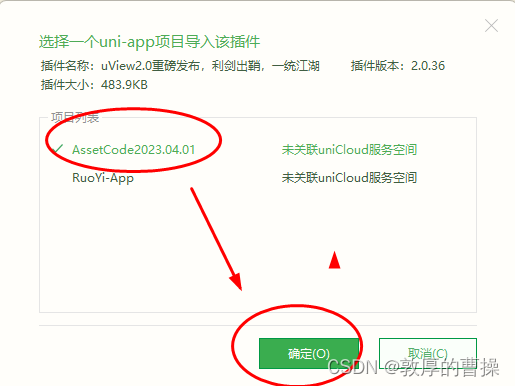
【RuoYi移动端】uniApp导入和引用uView2.0插件
一、打开uiew官网 安装 | uView 2.0 - 全面兼容 nvue 的 uni-app 生态框架 - uni-app UI 框架uView UI,是 uni-app 生态最优秀的 UI 框架,全面的组件和便捷的工具会让您信手拈来,如鱼得水https://uviewui.com/components/install.html 也可直…...

etcd 备份还原
etcd 备份还原 查看 etcdctl 是否已经安装 # quick check if etcdctl is available or not ETCDCTL_API3 etcdctl --help | head安装 etcdctl # 获取 etcd 版本信息 kubectl exec -it etcd-master -n kube-system -- /bin/sh -c ETCDCTL_API3 /usr/local/bin/etcd --version…...

LInux之chrony服务器
目录 场景 重要性 LInux的两个时钟 硬件时钟 系统时钟 NTP协议 Chrony介绍 定义 组成 --- chronyd和chronyc 安装与配置 安装 Chrony配置文件分析 同步时间服务器 chronyc命令 chronyc sources输出分析 其它命令 查看时间服务器的状态 查看时间服务器是否在线 …...

《Flink学习笔记》——第七章 处理函数
为了让代码有更强大的表现力和易用性,Flink 本身提供了多层 API 在更底层,我们可以不定义任何具体的算子(比如 map,filter,或者 window),而只是提炼出一个统一的“处理”(process&a…...
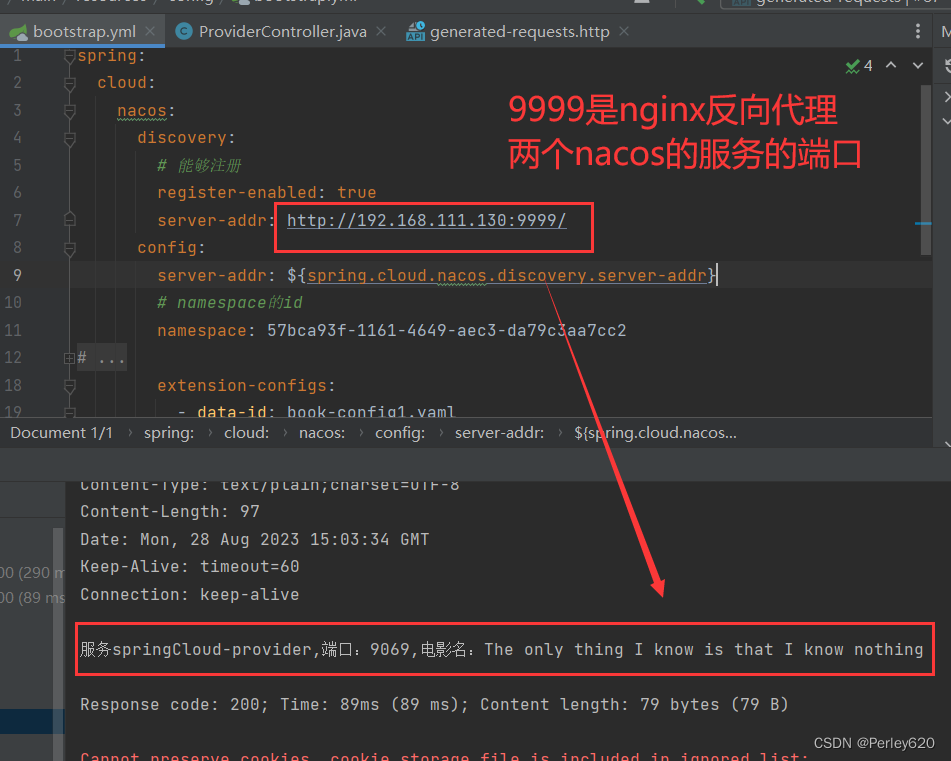
Nacos基础(3)——nacos+nginx 集群的配置和启动 端口开放 nginx反向代理nacos集群
目录 引出nacos集群nginx反向代理nacos集群停止单例nacos准备8848和8858修改cluster.conf配置【配置】修改启动配置文件【配置】开放8858的端口分别以集群方式启动【启动】前端访问查看生产者测试8858nacos nginx反向代理配置代理tcp代理http启动nginx反向代理容器生产者访问测…...

传承精神 缅怀伟人——湖南多链优品科技有限公司赴韶山开展红色主题活动
8月27日上午, 湖南多链优品科技有限公司全体员工怀着崇敬之情,以红色文化为引领,参加了毛泽东同志诞辰130周年的纪念活动。以董事长程小明为核心的公司班子成员以及全国优秀代表近70人一行专赴韶山,缅怀伟人毛泽东同志的丰功伟绩。…...

安全知识普及-如何创建一个安全的密码
文章目录 安全密码的特点创建安全密码的方法为何要创建一个安全的密码推荐阅读 安全密码是一种强化的密码,旨在提供更高级别的安全性,以防止未经授权的访问、数据泄露和其他安全威胁。 安全密码的特点 安全密码,有七大特点,特点如…...

Lua基础知识
文章目录 1. Lua简介1.1 设计目的:1.2 特性1.3 应用场景 2. Lua脚本学习2.1 安装2.2 lua操作2.3 lua案例 学习lua主要是为了后续做高性能缓存架构所准备的基础技术。可以先了解下基础,在实际使用时,再查缺补漏。 1. Lua简介 Lua 是一种轻量小…...

Java Math方法记录
Java 提供 java.lang.Math 类,很方便的进行数学运算。 Math 类是基于浮点数的运算,可能导致精度损失,不适用于高精度计算。 记录如下 常量 提供了两个常量, Math.PI :圆周率πMath.E :自然对数的底数 …...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...
