【力扣每日一题】2023.8.29 带因子的二叉树
目录
题目:
示例:
分析:
代码:
题目:
示例:

分析:
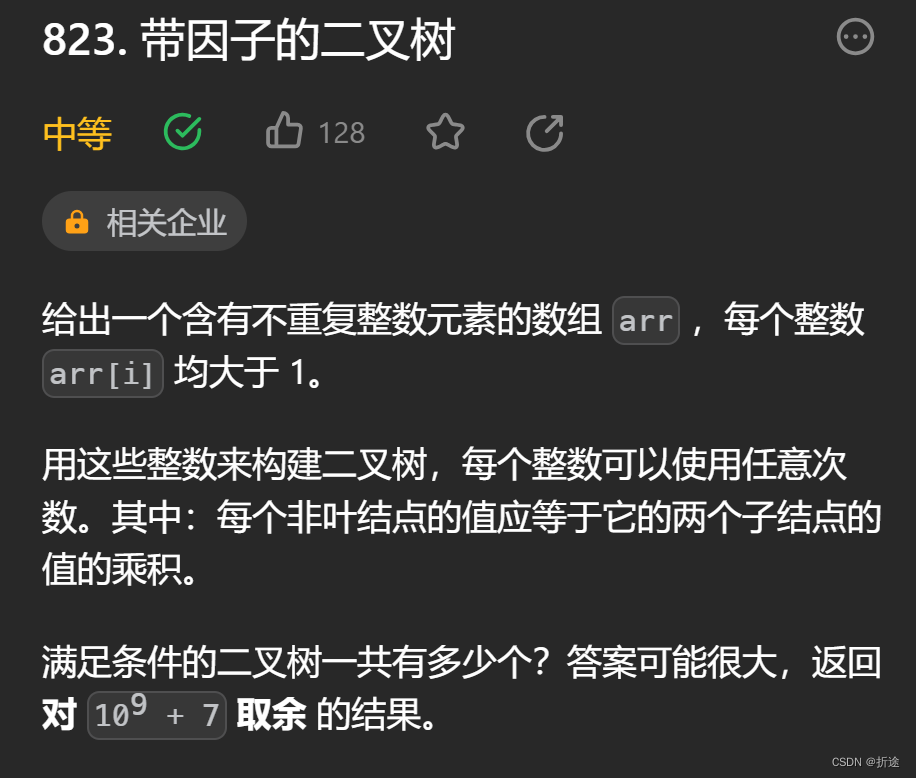
题目给我们一些元素,让我们用这些元素连接形成特定的二叉树,每种元素可以使用任意次数,形成的二叉树要求每个非叶子节点的值都为左右子树节点的值的乘积。
一个数要等于两个数的乘积,那么那两个数一定会比那一个数更小,所以我们可以从较小的数入手,那么我们首先将数组从小到大进行排序,接着从左到右,从小到大去遍历。
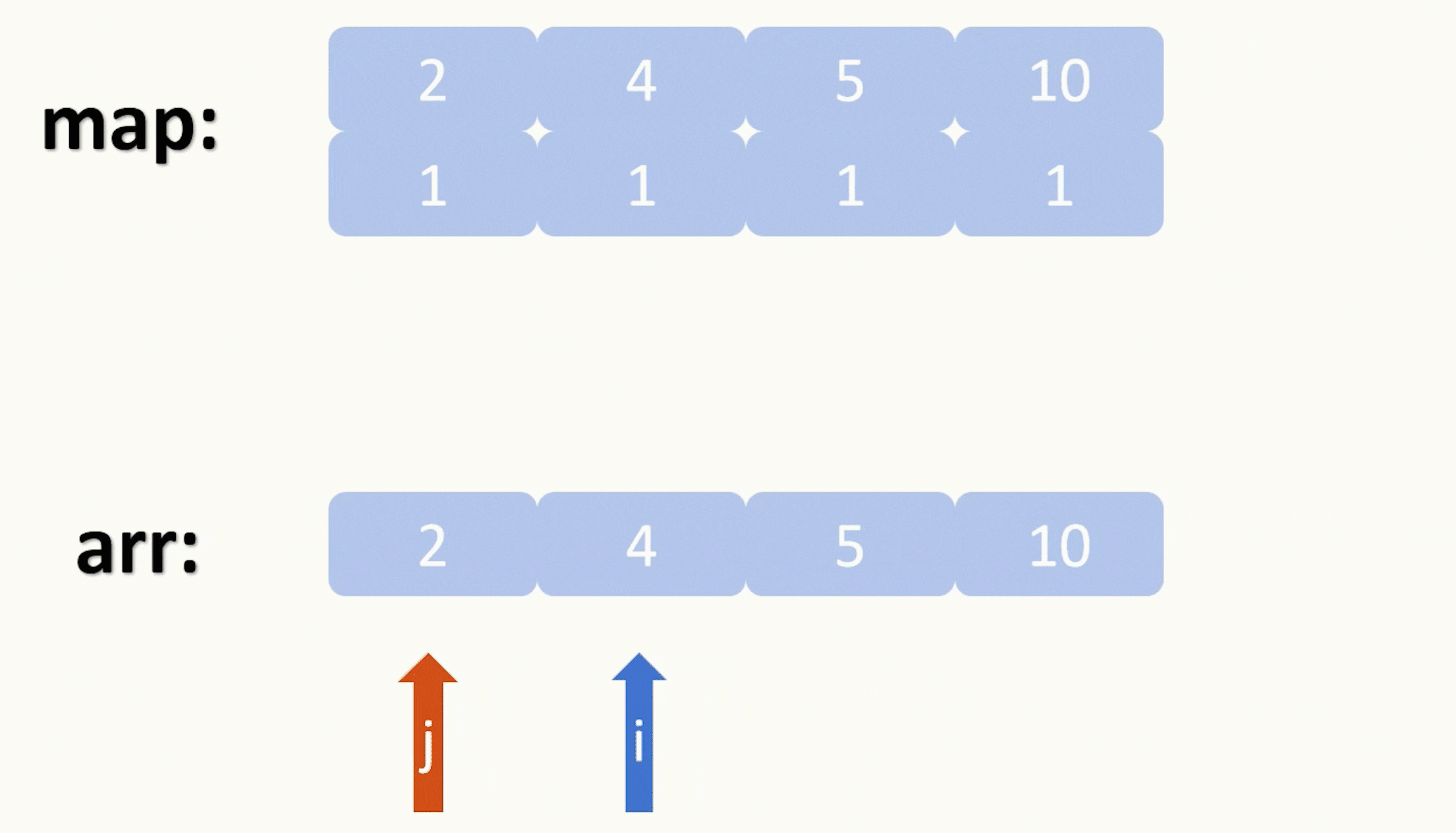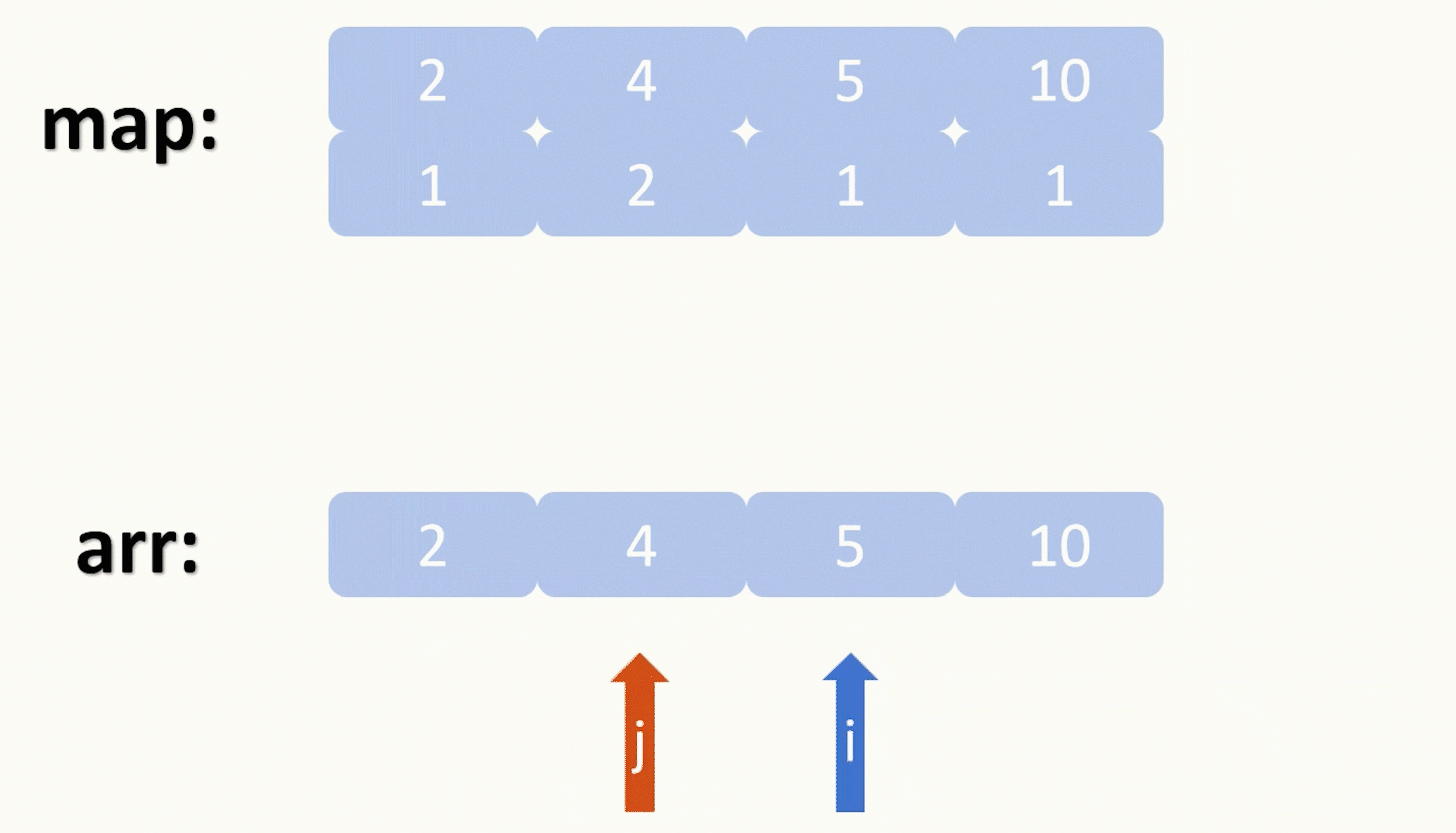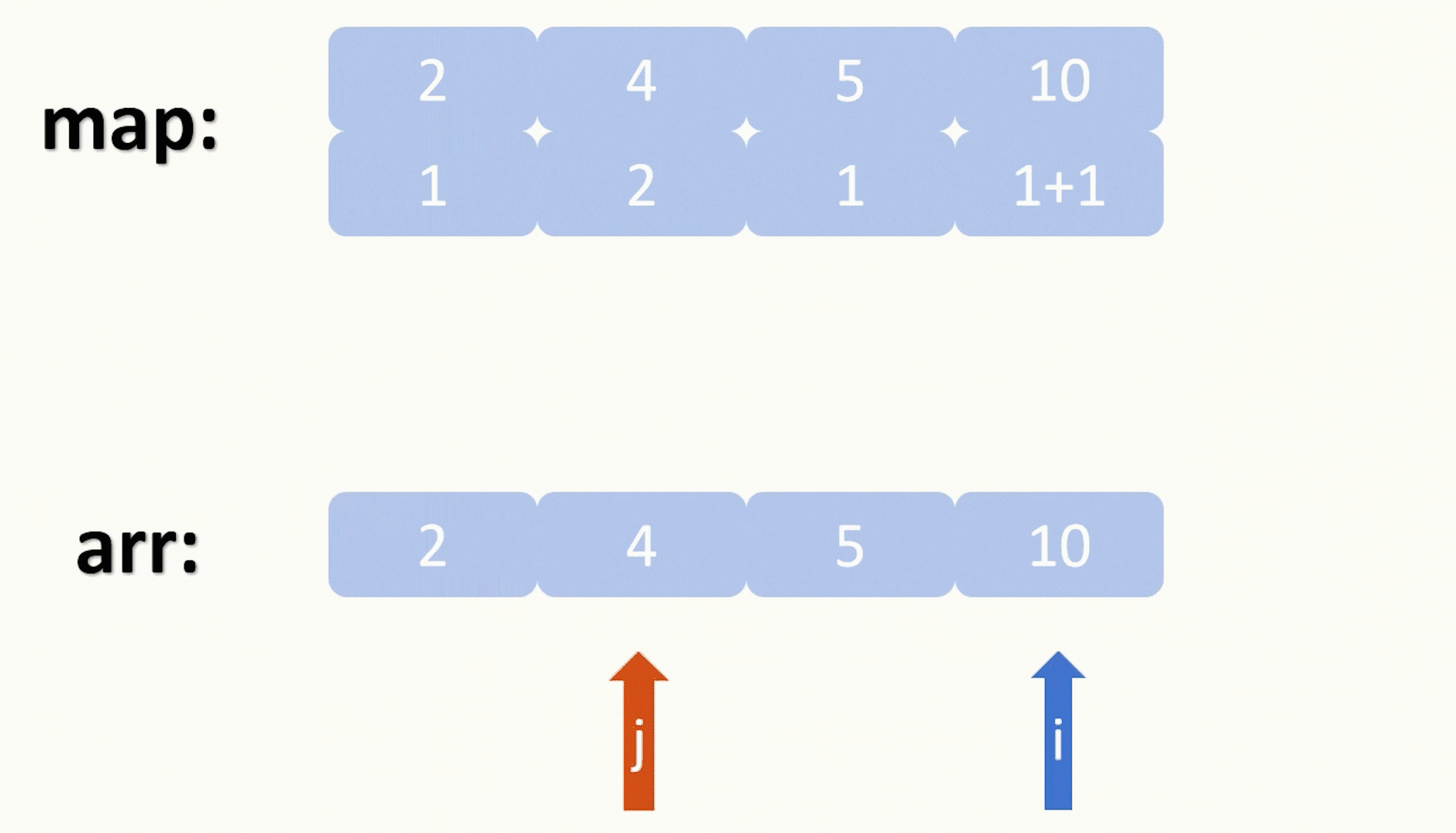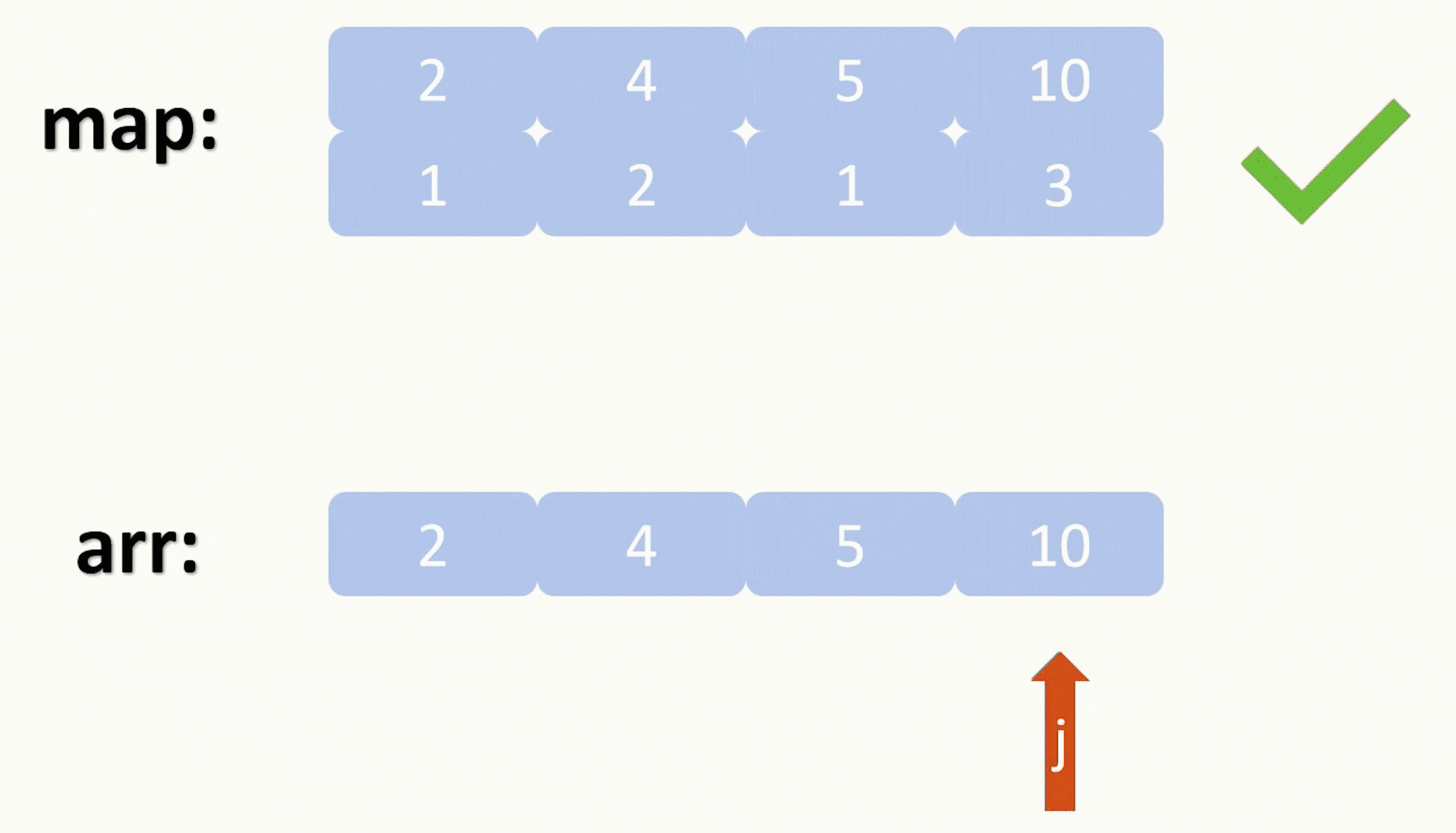
在遍历之前我们先做个预处理,我们用一个map来存住所有元素的值,以元素为键,值全部初始化为1。map每个键值对的含义就是以键为根节点能形参的二叉树有多少个,因为每个元素都可以以自身一个节点为一棵符合标准的二叉树,所以是初始化为1。
初始化完毕就开始遍历,我们需要套两层for循环,第一层去遍历每个根节点,去更新以当前节点为根节点所能形成的二叉树的数量,更新的方法就是第二层for循环去遍历比这个节点的值更小的元素,因为要相乘等于当前元素,那么乘数肯定是比当前元素更小的。
第一层遍历我们设下标为 i ,第二层下标为 j ,我们去寻找 arr[ i ] / arr[ j ] 这个元素在不在我们的map里,如果在,那么我们就把map里键为arr[ i ] 的键值对中的值加上以那两个乘数为根节点能形成的二叉树的数量的乘积,化简一下就是 m[ arr [ i ] ] += m[ arr[ i ] / arr[ j ] ] * m[ arr[ j ] ]。
由于我们是从小到大遍历的,所以我们每次都是会更新比后面的数更小的元素,以此元素为根节点能形参的二叉树,这样就可以得到推导出以后面较大的元素为根节点能形参的二叉树的数量。所以虽然我们没有用到dp数组,但它本质上来说还是属于动态规划。
还有一点要注意的就是题目有说要对结果取余10的九次方加7,所以为了避免数值溢出,我们每次操作都要做一个取余的操作。
代码:
class Solution {
public:int numFactoredBinaryTrees(vector<int>& arr) {int res=arr.size(); //单个节点可以单独为一棵树,初始化为数组长度sort(arr.begin(),arr.end());unordered_map<int,long>m; //用来记录以每个数为根节点的二叉树数目for(int i:arr){m[i]=1;}for(int i=0;i<arr.size();i++){for(int j=0;j<i;j++){//如果发现arr[i]整除arr[j]的数也在数组里,那么可以多组成的二叉树数目等于以arr[j]为根节点的二叉树数目乘上以另一个除数为根节点的二叉树数目.if(arr[i]%arr[j]==0&&m.find(arr[i]/arr[j])!=m.end()){int t=m[arr[i]/arr[j]]*m[arr[j]]%1000000007;m[arr[i]]+=t; //更新以arr[i]为根节点的二叉树数目.res+=t;res%=1000000007;}}}return res;}
};相关文章:

【力扣每日一题】2023.8.29 带因子的二叉树
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 题目给我们一些元素,让我们用这些元素连接形成特定的二叉树,每种元素可以使用任意次数,形成的二叉树要…...
origin导出pdf曲线超出边框
软件版本 软件版本Word2021Origin2021Adobe Acrobat Pro2023 问题描述 Origin导出的emf格式矢量图片,插入到Word中,显示正常,但是在使用Word导出→创建Adobe PDF→创建Adobe PDF导出PDF文件后,图片曲线就会超出边框,…...

由Android10适配到Android12时遇到相关编译失败问题
最近Android系统各大应用商店联合发出公告,处于个人隐私安全考虑,强制APP适配到Android 11及以上版本。下面是其中应用市场的公告(顺带提醒没适配的同学): 适配前的开发环境 名称版本Android studioGiraffe | 2022.3…...

高职教育应对ChatGPT应用的策略
一、完善顶层设计,提升技术水平 在推广ChatGPT平台的过程中,高职院校需要关注技术本身的问题。这就需要在国家和地方政府的引导下,引入更完善的技术顶层设计,提高人工智能在高职教育中的运用水平。具体来说,一方面需要…...

Linux 内核编译参数
文章目录 前言1 -Wall2 -Wundef3 -Wstrict-prototypes4 -Wno-trigraphs5 -fno-strict-aliasing6 -fno-common7 -Werror-implicit-function-declaration8 -Wno-format-security9 -fno-delete-null-pointer-checks10 -stdgnu89 前言 # cat /etc/os-release NAME"CentOS Lin…...

vscode使用anaconda自带的python环境在终端运行时报错
目录 具体报错内容官方翻译报错讲人话解决方法 具体报错内容 CommandNotFoundError: Your shell has not been properly configured to use conda activate. If your shell is Bash or a Bourne variant, enable conda for the current user with$ echo ". E:\Anaconda/e…...

葡萄叶病害识别(图像连续识别和视频识别,Python代码,pyTorch框架)
葡萄叶病害识别(图像连续识别和视频识别,Python代码,pyTorch框架)_哔哩哔哩_bilibili 葡萄数据集 第一个文件夹为 Grape Black Measles(葡萄黑麻疹)病害(3783张) Grape Black rot葡…...

Oracle drop删除表如何恢复
摘要: 在 Oracle 数据库管理中,DROP 命令的误操作可能导致数据不可挽回的丢失。然而,Oracle 提供了回收站(recycle bin)功能,允许用户在删除对象后的一段时间内恢复它们。本文将介绍如何查询、启用和管理回…...

5、监测数据采集物联网应用开发步骤(5.1)
监测数据采集物联网应用开发步骤(4) Sqlite3数据库读写操作开发、异常信息统一处理类开发 本章节需要调用sqlite3及mysql-connector 安装sqlite3 Pip3 install sqlite3 安装mysql-connector pip3 install mysql-connector 验证是否安装成功,python中运行下列…...

ZZULIOJ 1148: 组合三位数之一,Java
ZZULIOJ 1148: 组合三位数之一,Java 题目描述 把1、2、3、4、5、6、7、8、9组合成3个3位数,要求每个数字仅使用一次,使每个3位数均为完全平方数。按从小到大的顺序输出这三个三位数。 输入 无 输出 按从小到大的顺序输出这三个三位数&a…...

ROS功能包目录下CMakeLists.txt
1. add_execuble CMake基础教程(24)add_executable生成目标可执行文件 CMake中add_executable的使用 CMake中的add_executable命令用于使用指定的源文件向项目(project)添加可执行文件,其格式如下: add_executable(<name>…...

Python爬虫追踪新闻事件发展进程及舆论反映
目录 实现方案 1. 确定目标新闻源: 2. 确定关键词: 3. 使用网络爬虫获取新闻内容: 4. 提取和分析新闻文章: 5. 追踪新闻事件的发展进程: 6. 监测舆论反映: 7. 数据可视化: 完整代码示例…...

block层:7. 请求下发
blk_dispatch 源码基于5.10 1. blk_mq_sched_dispatch_requests void blk_mq_sched_dispatch_requests(struct blk_mq_hw_ctx *hctx) {// 队列struct request_queue *q hctx->queue;// 队列已停止或者被暂停if (unlikely(blk_mq_hctx_stopped(hctx) || blk_queue_quiesc…...

Matlab图像处理-平移运算
几何运算 几何运算又称为几何变换,是将一幅图像中的坐标映射到另外一幅图像中的新坐标位置,它不改变图像的像素值,只是改变像素所在的几何位置,使原始图像按照需要产生位置、形状和大小的变化。 图像几何运算的一般定义为&#…...

美创科技一体化智能化公共数据平台数据安全建设实践
公共数据是当今政府数字化转型的关键要素和未来价值释放的核心锚点,也是“网络强国”、“数字中国”的战略性资源。 作为数字化改革先行省份,近年来,浙江省以一体化智能化公共数据平台作为数字化改革的支撑总平台,实现了全省公共数…...
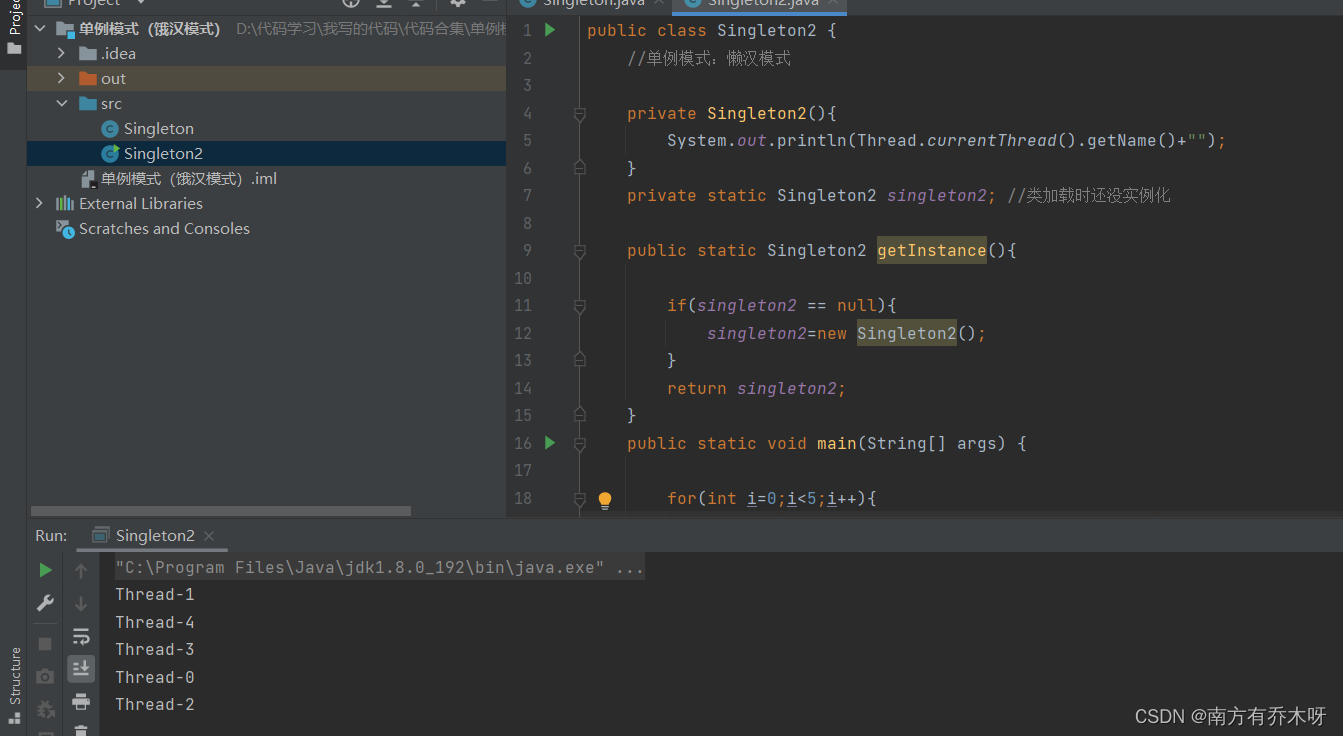
关于单例模式
单例模式的目的: 单例模式的目的和其他的设计模式的目的都是一样的,都是为了降低对象之间的耦合性,增加代码的可复用性,可维护性和可扩展性。 单例模式: 单例模式是一种常用的设计模式,用简单的言语说&am…...
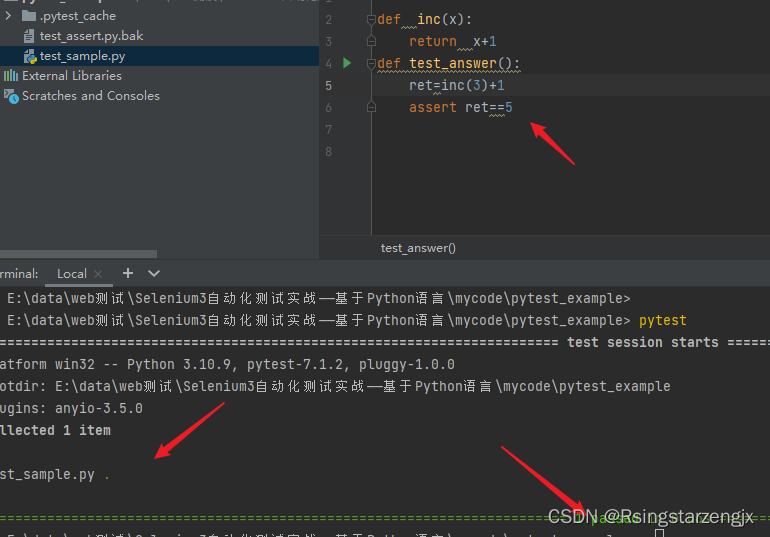
pytest笔记: pytest单元测试框架
第一步:安装 和查看版本 pycharm settings 查看 第二步: 编写test_example.py def inc(x):return x1 def test_answer():assert inc(4) 5 第三步:在当前路径下执行pytest 命令 PS E:\data\web测试\Selenium3自动化测试实战——基于Pyth…...
vulnhub Seattle-0.0.3
环境:vuluhub Seattle-0.0.3 1.catelogue处任意文件下载(目录穿越) http://192.168.85.139/download.php?item../../../../../../etc/passwd 有个admin目录,可以下载里面的文件进行读取 2.cltohes详情页面处(参数prod)存在sql报错注入 http://192.16…...

MYSQL 添加行号将行号写入到主键的列
MYSQL 添加行号 SELECT rownum: rownum 1 AS rownum, a.* FROM(SELECT rownum : 0) t,is_afxt.hk_vehicle a--或者(假设CREATED_TIME日期列数据不重复) select (select count(1)1 from is_afxt.hk_vehicle b where b.CREATED_TIME < a.CREATED_TIME) rownum ,a.* from i…...

前端命令npm 、 cnpm、 pnpm、yarn 、 npx、nvm的区别
大名鼎鼎的npm(Node Package Manager)是随同NodeJS一起安装的包管理工具,NPM本身也是Node.js的一个模块。 npm的含义有两层: npm服务器,npm服务器网址为https://www.npmjs.org,npm是 Node 包的标准发布平台,用于 Node 包的发布、…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
