算法面试-深度学习面试题整理(2024.8.29开始,每天下午持续更新....)
一、无监督相关(聚类、异常检测)
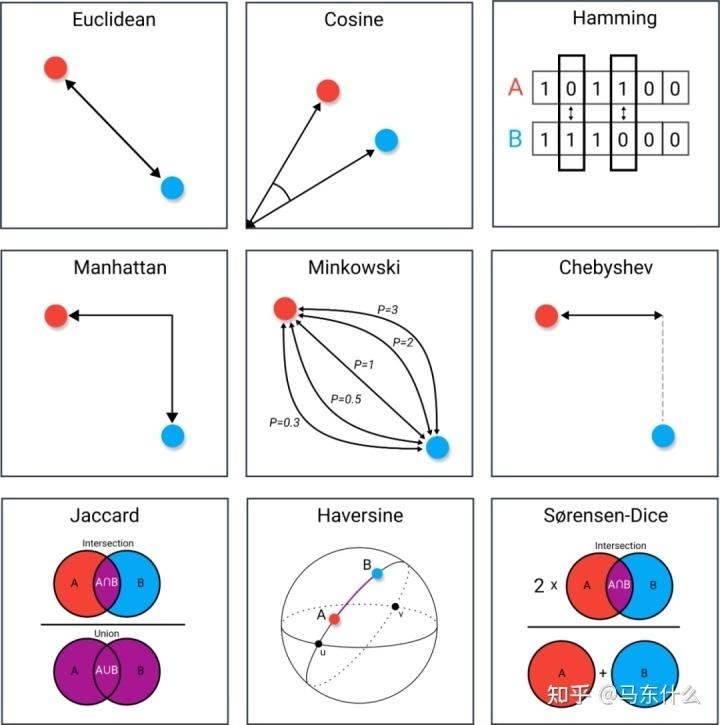
1、常见的距离度量方法有哪些?写一下距离计算公式。
1)连续数据的距离计算:
闵可夫斯基距离家族:

当p = 1时,为曼哈顿距离;p= 2时,为欧式距离;p ->∞时,就是切比雪夫距离。
余弦距离:
![]()
其中,A 和B是要比较的两个向量,⋅ 表示向量的点积(内积),∥A∥ 和 ∥B∥ 分别表示向量 A 和 B的欧几里德范数(也称为 L2 范数)。余弦距离的值范围在[0,2],取值越小表示两个向量越相似,取值越大表示两个向量越不相似。如果两个向量方向相同,则余弦距离为 0,表示完全相似;如果两个向量方向相反,则余弦距离为 2,表示完全不相似。请注意,有时也可以用余弦相似性(Cosine Similarity)来衡量向量的相似性,它是余弦距离的补数,即1−Cosine Distance。余弦相似性的取值范围在 [-1, 1],取值越大表示两个向量越相似,取值越小表示越不相似。
2)离散数据的距离计算
杰卡尔德(Jaccard)距离:A,B集合的交集/A,B集合的并集
汉明距离:表示两个等长字符串在对应位置上不同字符的数目
2、常见的聚类算法有哪些?
主要有基于划分、基于密度、基于网络、层次聚类等,除此之外聚类和其他领域也有很多结合形成的交叉领域比如半监督聚类、深度聚类、集成聚类等。
3、Kmeans的原理是什么?
Kmeans是一种基于划分的聚类,中心思想是类内距离尽量小,类间距离尽量大,主要算法过程如下:
- 初始K个质心,作为初始的K个簇的中心点,K为人工设定的超参数;
- 所有样本点n分别计算和K个质心的距离,这里的距离是人工定义的可以是不同距离计算方法,每个样本点和k个质心中最近的质心划分为1类簇;
- 重新计算质心,方法是针对簇进行聚合计算,kmeans中使用简单平均的方法进行聚合计算,也可以使用中位数等方式进行计算;
- 重复上述过程直到达到预定的迭代次数或质心不再发生明显变化。
- kmeans的损失函数是:

其中,||xi - cj|| 表示数据点 xi 到簇中心 cj 的欧氏距离,I(condition) 是一个指示函数,当 condition 成立时为 1,否则为 0。J越小,说明样本聚合程度越高。
4、Kmeans的初始点怎么选择,不同的初始点选择有哪些缺陷?该怎么解决?
- 随机初始化:随机选取K个样本点作为初始质心,缺陷在于如果选择到的质心距离很接近落在同个簇内,则迭代的结果可能比较差,因为最终迭代出来的质心点会落在簇内。最理想的状态是K个质心正好是K个簇,由于随机初始化的随机性,可以考虑多次进行随机初始化,选择聚合结果最优的一次。
- 随机分取初始化:即将所有样本点随机赋予1个簇的编号,则所有样本点最后会有K个编号,然后进行组平均,即对于同一个簇的样本进行平均得到初始化质心。相对于随机初始化,初始化质心会更鲁棒一些,但是仍旧存在随机初始化的缺陷,仅仅是缓解。
5、Kmeans聚的是特征还是样本?特征的距离如何计算?
一般情况下是对样本聚类,如果对特征聚类则处理方式也简单,对原始的输出进行转置。其目的和做相关系数类似,如果两个特征高度相关,例如收入和资产水平,则两个特征的距离相对较小,但是一般不可行,因为转置后维度很高,例如有100万个样本则有100万的维度,计算上不现实,高维数据的距离度量也是无效的,不如直接计算相关系数。
6、Kmeans如何调优?
- 初始化策略调参
- k的大小调参,手工方法,手肘法为代表
- 数据归一化和异常样本的处理
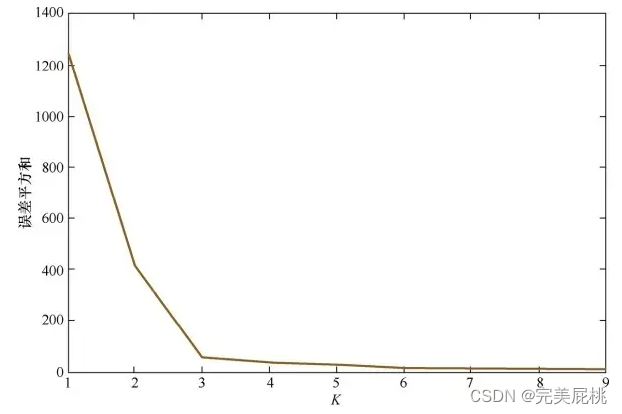
7、介绍一下手肘法。
手肘法纵轴是聚类效果的评估指标,根据具体的问题而定,如果聚类是作为单独的任务存在则使用SSE(损失函数)或轮廓系数这类的metric作为纵坐标,然后找到metric最好且k最小的结果,对应的k为最终的选择。手肘法自动化时,只需计算k = n 和 k = n+1之间的斜率,当斜率n和n-1,斜率n+1和斜率n,斜率n+2和斜率n+1的差值均小于固定阈值时即可停止。
8、kmeans的缺点如何解决?
- 对异常样本很敏感,簇心会因为异常样本被拉得很远。异常样本是指在某些维度上取值特别大或者特别小的样本,欧式距离中默认所有特征是相互独立的,异常样本会产生影响。解决方法是做好预处理,将异常样本剔除或者修正。
- K值很难确定。解决方法是针对k调参。
- 只能拟合球形簇,对于流形簇等不规则簇可能存在簇重叠的问题,效果差。这种情况可能不再适用于Kmeans算法,考虑换算法。
- 无法处理离散特征,缺失特征。
- 无法保证全局最优。解决方法是跑多次,取不同的局部最优里的最优。
相关文章:

算法面试-深度学习面试题整理(2024.8.29开始,每天下午持续更新....)
一、无监督相关(聚类、异常检测) 1、常见的距离度量方法有哪些?写一下距离计算公式。 1)连续数据的距离计算: 闵可夫斯基距离家族: 当p 1时,为曼哈顿距离;p 2时,为欧…...

Maven之高版本的 lombok 和 tomcat 7 插件冲突问题
高版本的 lombok 和 tomcat 7 插件冲突问题 在开发期间,当我们使用 tomcat7-maven-plugin 来作为运行环境运行我们项目使,如果我们项目中使用了 1.16.20 及以上版本的 lombok 包,项目启动时会报错: for annotations org.apache.…...

微信小程序申请
方案说明: 微信小程序申请步骤有两个过程,目前采用的是第二种方案 第一种方案:直接向微信申请微信小程序 第二种方案:先申请公众号后再通过公众号快速注册并申请小程序 无论申请公众号还是小程序都需要微信认证,微…...

ffmpeg 配合Fiddler抓包操作
首先需要安装和配置ffmpeg 1.扩大音频2倍 ffmpeg -i 2.mp3 -filter:a "volume2.0" 3.mp32.扩大音频4倍 ffmpeg -i 2.mp3 -filter:a "volume4.0" 3.mp33.音视频合成(m4s视频和mp3音频合成) ffmpeg -i 1.m4s -i 3.mp3 -vcodec cop…...

美团面试拷打:ConcurrentHashMap 为何不能插入 null?HashMap 为何可以?
周末的时候,有一位小伙伴提了一些关于 ConcurrentHashMap 的问题,都是他最近面试遇到的。原提问如下(星球原贴地址:https://t.zsxq.com/11jcuezQs ): 整个提问看着非常复杂,其实归纳来说就是两个问题: ConcurrentHashMap 为什么 key 和 value 不能为 null?ConcurrentH…...
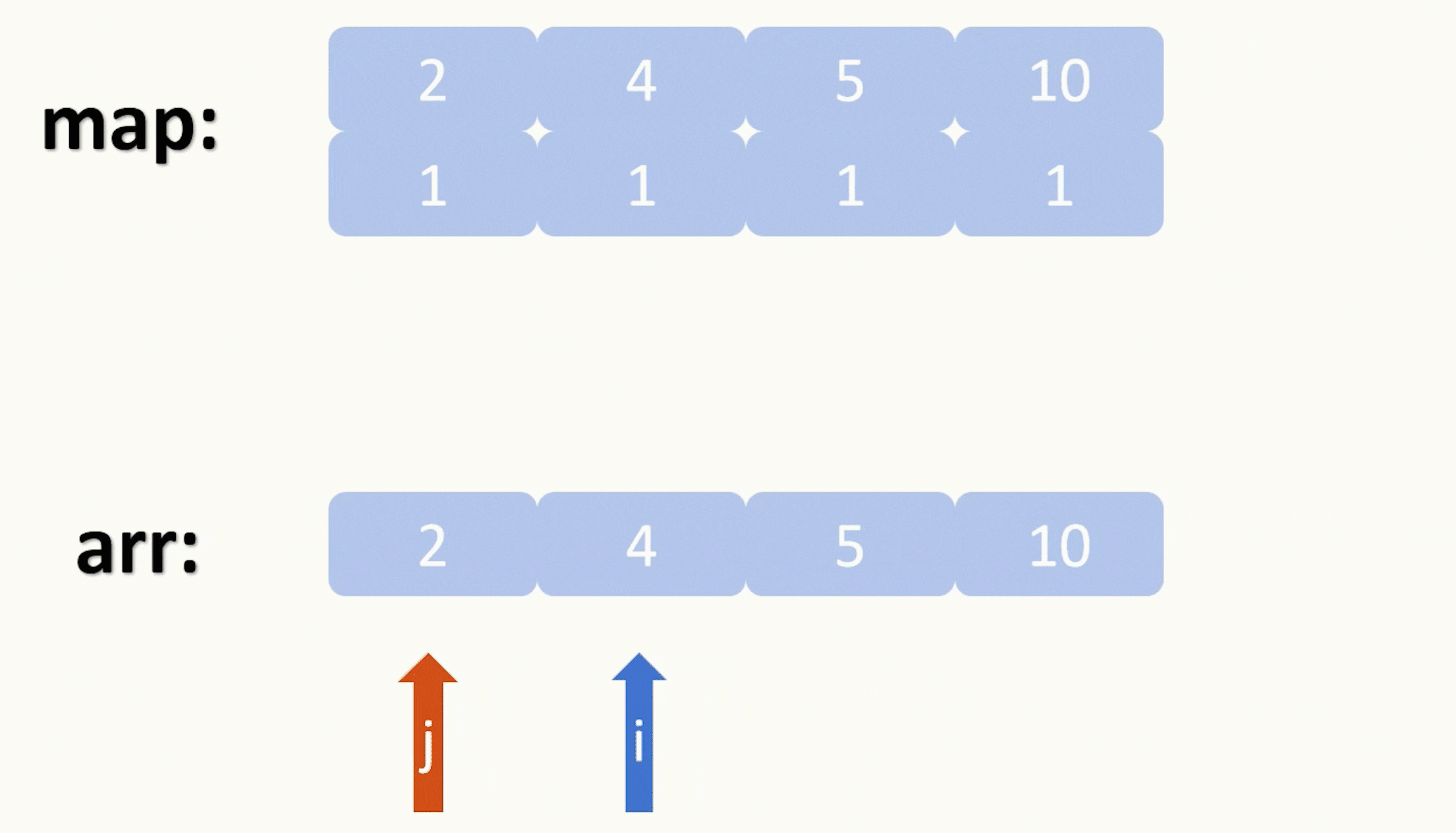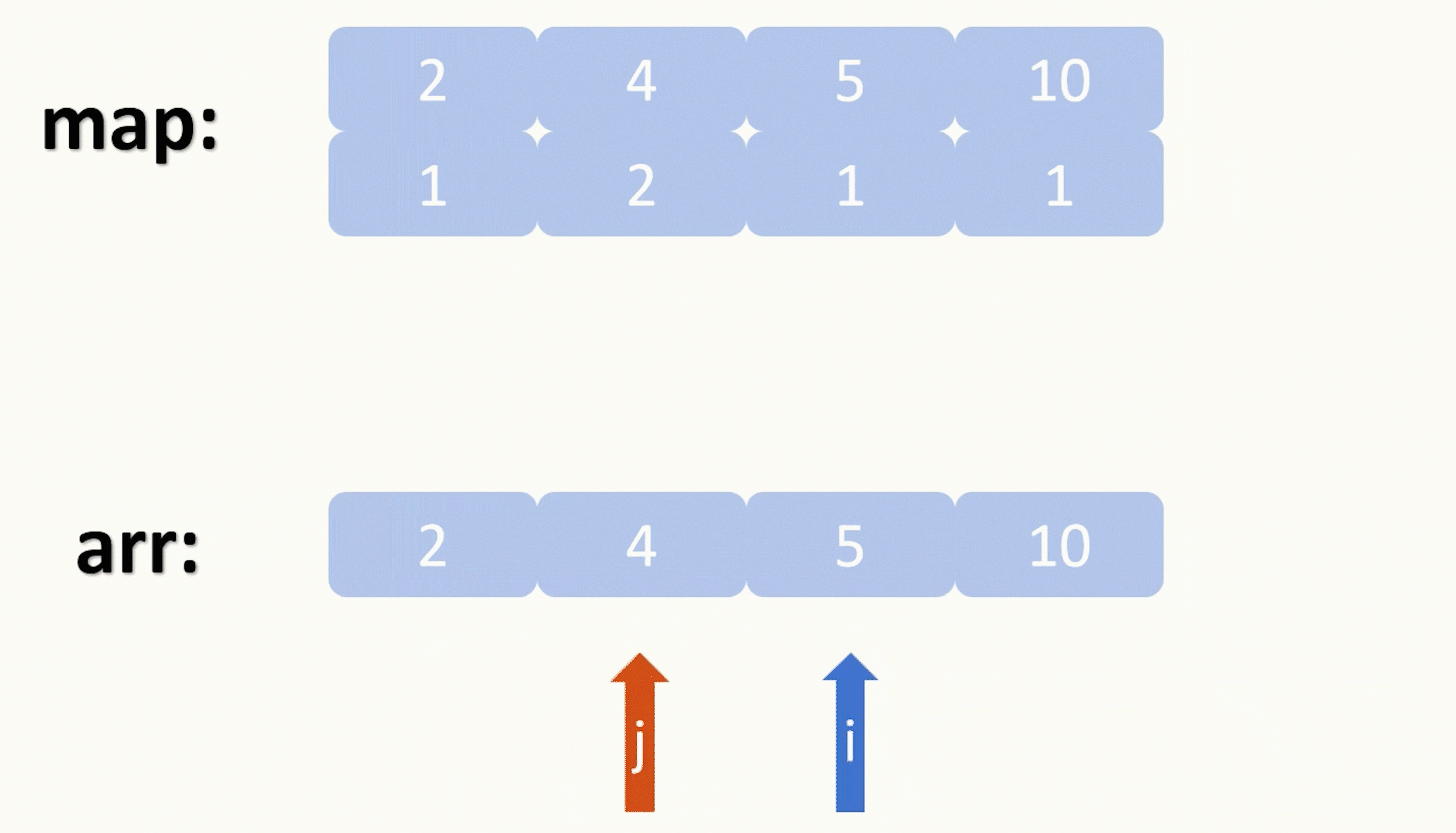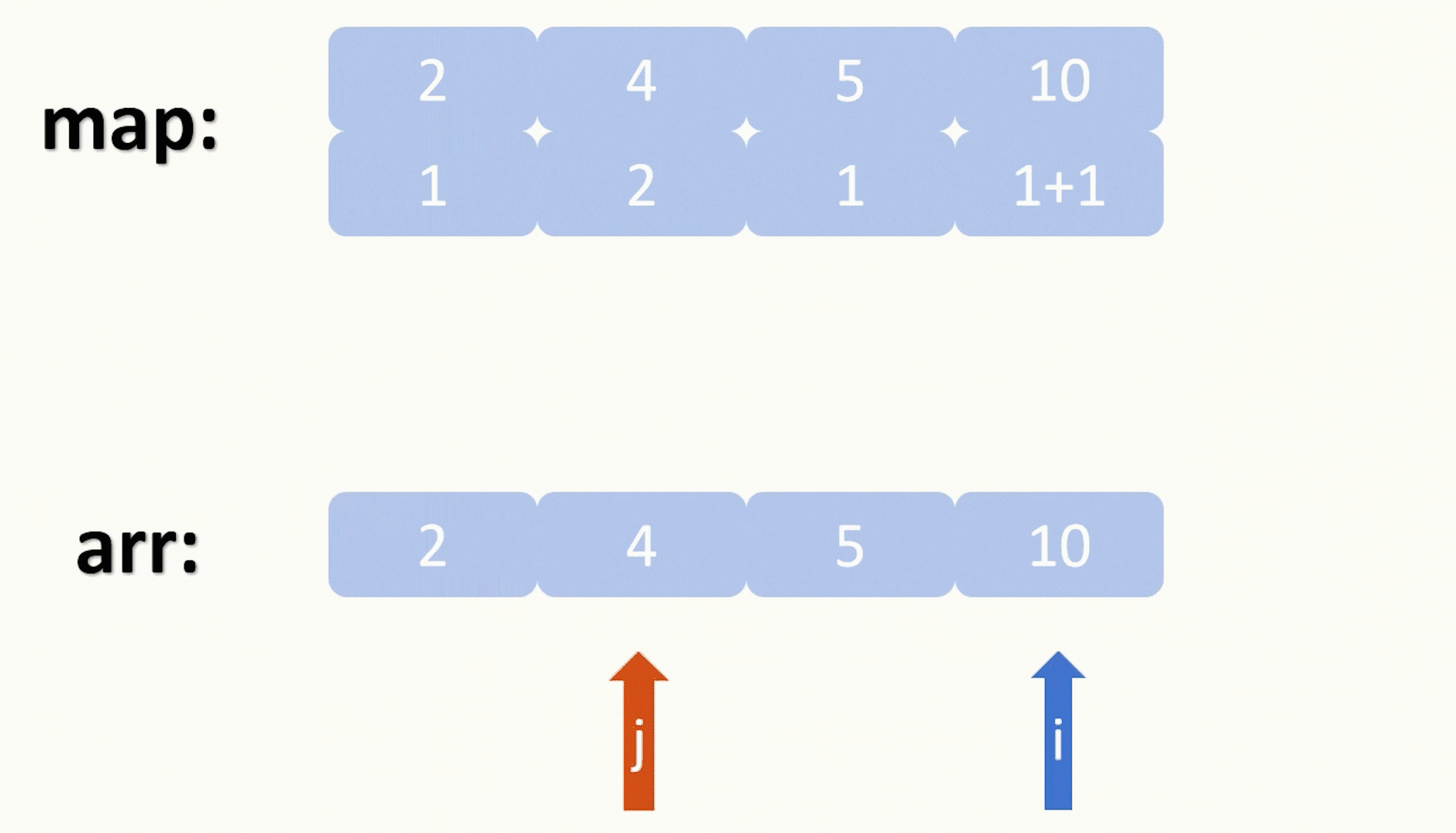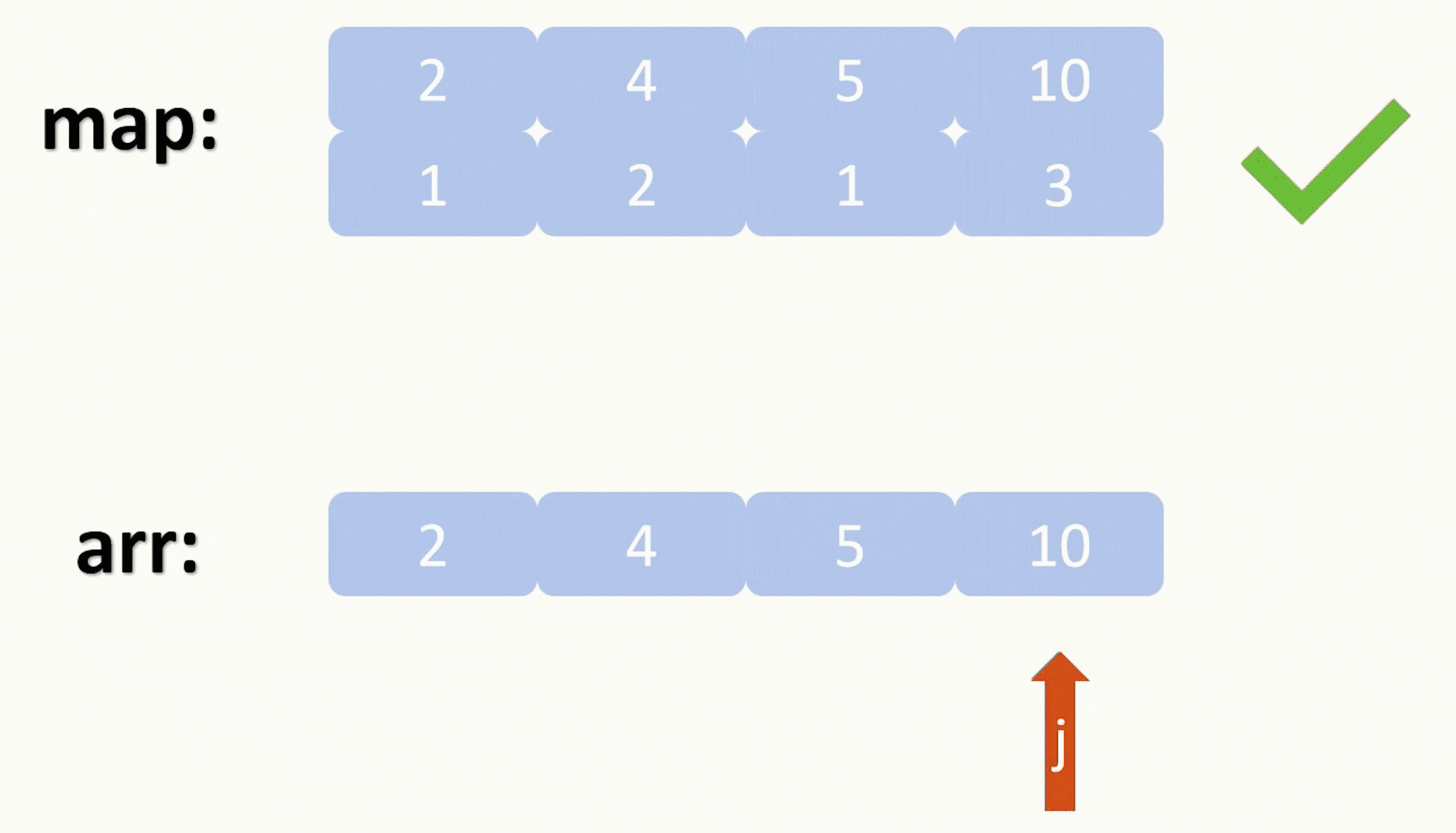
【力扣每日一题】2023.8.29 带因子的二叉树
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 题目给我们一些元素,让我们用这些元素连接形成特定的二叉树,每种元素可以使用任意次数,形成的二叉树要…...
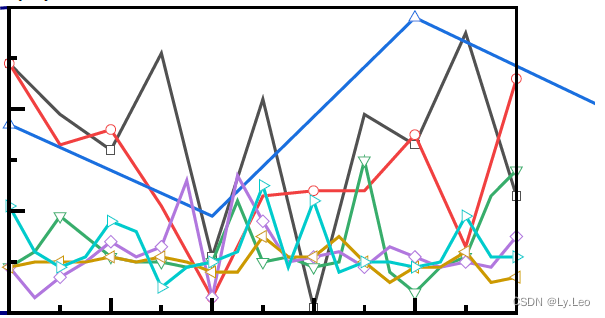
origin导出pdf曲线超出边框
软件版本 软件版本Word2021Origin2021Adobe Acrobat Pro2023 问题描述 Origin导出的emf格式矢量图片,插入到Word中,显示正常,但是在使用Word导出→创建Adobe PDF→创建Adobe PDF导出PDF文件后,图片曲线就会超出边框,…...

由Android10适配到Android12时遇到相关编译失败问题
最近Android系统各大应用商店联合发出公告,处于个人隐私安全考虑,强制APP适配到Android 11及以上版本。下面是其中应用市场的公告(顺带提醒没适配的同学): 适配前的开发环境 名称版本Android studioGiraffe | 2022.3…...

高职教育应对ChatGPT应用的策略
一、完善顶层设计,提升技术水平 在推广ChatGPT平台的过程中,高职院校需要关注技术本身的问题。这就需要在国家和地方政府的引导下,引入更完善的技术顶层设计,提高人工智能在高职教育中的运用水平。具体来说,一方面需要…...

Linux 内核编译参数
文章目录 前言1 -Wall2 -Wundef3 -Wstrict-prototypes4 -Wno-trigraphs5 -fno-strict-aliasing6 -fno-common7 -Werror-implicit-function-declaration8 -Wno-format-security9 -fno-delete-null-pointer-checks10 -stdgnu89 前言 # cat /etc/os-release NAME"CentOS Lin…...

vscode使用anaconda自带的python环境在终端运行时报错
目录 具体报错内容官方翻译报错讲人话解决方法 具体报错内容 CommandNotFoundError: Your shell has not been properly configured to use conda activate. If your shell is Bash or a Bourne variant, enable conda for the current user with$ echo ". E:\Anaconda/e…...

葡萄叶病害识别(图像连续识别和视频识别,Python代码,pyTorch框架)
葡萄叶病害识别(图像连续识别和视频识别,Python代码,pyTorch框架)_哔哩哔哩_bilibili 葡萄数据集 第一个文件夹为 Grape Black Measles(葡萄黑麻疹)病害(3783张) Grape Black rot葡…...

Oracle drop删除表如何恢复
摘要: 在 Oracle 数据库管理中,DROP 命令的误操作可能导致数据不可挽回的丢失。然而,Oracle 提供了回收站(recycle bin)功能,允许用户在删除对象后的一段时间内恢复它们。本文将介绍如何查询、启用和管理回…...

5、监测数据采集物联网应用开发步骤(5.1)
监测数据采集物联网应用开发步骤(4) Sqlite3数据库读写操作开发、异常信息统一处理类开发 本章节需要调用sqlite3及mysql-connector 安装sqlite3 Pip3 install sqlite3 安装mysql-connector pip3 install mysql-connector 验证是否安装成功,python中运行下列…...

ZZULIOJ 1148: 组合三位数之一,Java
ZZULIOJ 1148: 组合三位数之一,Java 题目描述 把1、2、3、4、5、6、7、8、9组合成3个3位数,要求每个数字仅使用一次,使每个3位数均为完全平方数。按从小到大的顺序输出这三个三位数。 输入 无 输出 按从小到大的顺序输出这三个三位数&a…...

ROS功能包目录下CMakeLists.txt
1. add_execuble CMake基础教程(24)add_executable生成目标可执行文件 CMake中add_executable的使用 CMake中的add_executable命令用于使用指定的源文件向项目(project)添加可执行文件,其格式如下: add_executable(<name>…...

Python爬虫追踪新闻事件发展进程及舆论反映
目录 实现方案 1. 确定目标新闻源: 2. 确定关键词: 3. 使用网络爬虫获取新闻内容: 4. 提取和分析新闻文章: 5. 追踪新闻事件的发展进程: 6. 监测舆论反映: 7. 数据可视化: 完整代码示例…...

block层:7. 请求下发
blk_dispatch 源码基于5.10 1. blk_mq_sched_dispatch_requests void blk_mq_sched_dispatch_requests(struct blk_mq_hw_ctx *hctx) {// 队列struct request_queue *q hctx->queue;// 队列已停止或者被暂停if (unlikely(blk_mq_hctx_stopped(hctx) || blk_queue_quiesc…...

Matlab图像处理-平移运算
几何运算 几何运算又称为几何变换,是将一幅图像中的坐标映射到另外一幅图像中的新坐标位置,它不改变图像的像素值,只是改变像素所在的几何位置,使原始图像按照需要产生位置、形状和大小的变化。 图像几何运算的一般定义为&#…...

美创科技一体化智能化公共数据平台数据安全建设实践
公共数据是当今政府数字化转型的关键要素和未来价值释放的核心锚点,也是“网络强国”、“数字中国”的战略性资源。 作为数字化改革先行省份,近年来,浙江省以一体化智能化公共数据平台作为数字化改革的支撑总平台,实现了全省公共数…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...
