【人工智能】—_不确定性、先验概率_后验概率、概率密度、贝叶斯法则、朴素贝叶斯_、最大似然估计
【人工智能】— 不确定性、先验概率/后验概率、概率密度、贝叶斯法则、朴素贝叶斯
文章目录
- 【人工智能】— 不确定性、先验概率/后验概率、概率密度、贝叶斯法则、朴素贝叶斯
- 不确定性
- 不确定性与理性决策
- 基本概率符号
- 先验概率(无条件概率)/后验概率(条件概率)
- 随机变量
- 概率密度
- 联合概率分布
- 公理
- 完全联合分布
- 概率演算
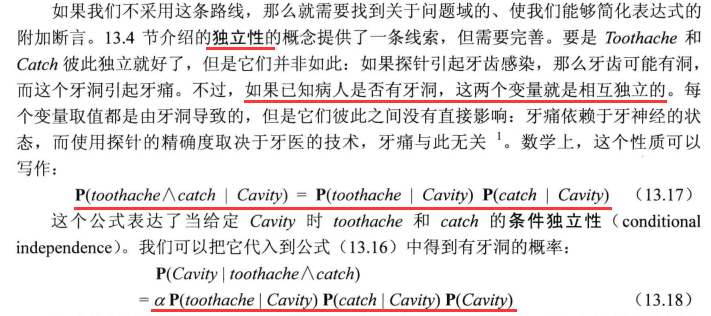
- 独立性
- 贝叶斯法则
- 例1
- 例2
- 使用贝叶斯规则:合并证据
- 朴素贝叶斯
- 最大似然估计
- 小结
不确定性

不确定性与理性决策


基本概率符号
先验概率(无条件概率)/后验概率(条件概率)



随机变量


概率密度

联合概率分布




公理

完全联合分布
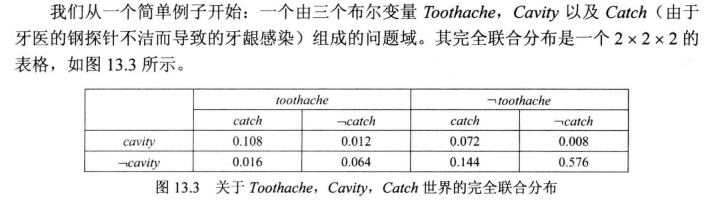
概率演算

独立性
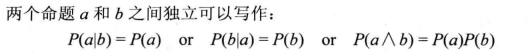

贝叶斯法则



例1
你有两个信封可供选择。一个信封里有一个红球(价值100美元)和一个黑球,另一个信封里有两个黑球(价值为零)。

你随机选择一个信封,然后从该信封中随机取出一个球,结果是黑色的。
此时,你可以选择是否换另一个信封。问题是,你应该换还是不换?
E: envelope, 1表示有一个红球的信封,2表示都是黑球的信封 1 = ( R , B ) , 2 = ( B , B ) 1=(R,B), 2=(B,B) 1=(R,B),2=(B,B)
B: the event of drawing a black ball 拿到一个黑棋的事件
贝叶斯法则: P ( E ∣ B ) = P ( B ∣ E ) P ( E ) P ( B ) 贝叶斯法则:\\{}\\P(E|B) = \frac{P(B|E)P(E)}{P(B)} 贝叶斯法则:P(E∣B)=P(B)P(B∣E)P(E)
We want to compare 比较: P ( E = 1 ∣ B ) 比较:P(E=1|B) 比较:P(E=1∣B) vs. P ( E = 2 ∣ B ) P(E=2|B) P(E=2∣B)
在红球信封拿到黑球: P ( B ∣ E = 1 ) = 0.5 在黑球信封拿到黑球: P ( B ∣ E = 2 ) = 1 在红球信封拿到黑球:P(B|E=1) = 0.5 \\在黑球信封拿到黑球:P(B|E=2) = 1 在红球信封拿到黑球:P(B∣E=1)=0.5在黑球信封拿到黑球:P(B∣E=2)=1
拿到 1 、 2 信封的概率相同: P ( E = 1 ) = P ( E = 2 ) = 0.5 拿到1、2信封的概率相同:P(E=1) = P(E=2) = 0.5 拿到1、2信封的概率相同:P(E=1)=P(E=2)=0.5
抽到黑球的概率: B 在 E 取值上的边缘概率 P ( B ) = P ( B ∣ E = 1 ) P ( E = 1 ) + P ( B ∣ E = 2 ) P ( E = 2 ) = ( 0.5 ) ( 0.5 ) + ( 1 ) ( 0.5 ) = 0.75 \begin{aligned} &抽到黑球的概率:\\&{B在E取值上的边缘概率}\\ P(B) &= P(B|E=1)P(E=1) + P(B|E=2)P(E=2) \\ &= (0.5)(0.5) + (1)(0.5) \\ &= 0.75 \\ \end{aligned} P(B)抽到黑球的概率:B在E取值上的边缘概率=P(B∣E=1)P(E=1)+P(B∣E=2)P(E=2)=(0.5)(0.5)+(1)(0.5)=0.75
已经抽到一个黑球,此信封是红球信封的概率: P ( E = 1 ∣ B ) = P ( B ∣ E = 1 ) P ( E = 1 ) P ( B ) = ( 0.5 ) ( 0.5 ) ( 0.75 ) = 1 3 已经抽到一个黑球,此信封是红球信封的概率:\\{} \\P(E=1|B) = \frac{P(B|E=1)P(E=1)}{P(B)} = \frac{(0.5)(0.5)}{(0.75)} = \frac{1}{3} 已经抽到一个黑球,此信封是红球信封的概率:P(E=1∣B)=P(B)P(B∣E=1)P(E=1)=(0.75)(0.5)(0.5)=31
已经抽到一个黑球,此信封是黑球信封的概率: P ( E = 2 ∣ B ) = P ( B ∣ E = 2 ) P ( E = 2 ) P ( B ) = ( 1 ) ( 0.5 ) ( 0.75 ) = 2 3 已经抽到一个黑球,此信封是黑球信封的概率:\\{} \\P(E=2|B) = \frac{P(B|E=2)P(E=2)}{P(B)} = \frac{(1)(0.5)}{(0.75)} = \frac{2}{3} 已经抽到一个黑球,此信封是黑球信封的概率:P(E=2∣B)=P(B)P(B∣E=2)P(E=2)=(0.75)(1)(0.5)=32
通过计算可得,抽到黑球后信封为 1 的概率为 1 / 3 , 信封为 2 的概率为 2 / 3 。因此,更换信封可以提高获得红球的概率。 通过计算可得,抽到黑球后信封为 1 的概率为 1/3,\\信封为 2 的概率为 2/3。因此,更换信封可以提高获得红球的概率。 通过计算可得,抽到黑球后信封为1的概率为1/3,信封为2的概率为2/3。因此,更换信封可以提高获得红球的概率。
例2
一位医生进行一项测试,该测试有99%的可靠性,即99%的生病者测试结果为阳性,99%的健康者测试结果为阴性。这位医生估计整个人口中有1%的人是生病的。
因此,对于测试结果为阳性的患者,他是生病的概率是多少呢?
我们可以使用贝叶斯定理来计算患者生病的条件概率。设事件 S 表示患者生病,事件 T 表示测试结果为阳性。则所求的条件概率为:
P ( S ∣ T ) = P ( T ∣ S ) P ( S ) P ( T ) P(S|T) = \frac{P(T|S)P(S)}{P(T)} P(S∣T)=P(T)P(T∣S)P(S)
其中, P ( T ∣ S ) P(T|S) P(T∣S) 表示患者生病的条件下,测试结果为阳性的概率, P ( S ) P(S) P(S) 表示患者生病的先验概率, P ( T ) P(T) P(T) 表示测试结果为阳性的概率。
根据题目中给出的数据,我们有: P ( T ∣ S ) = 0.99 根据题目中给出的数据,我们有:\\P(T|S) = 0.99 根据题目中给出的数据,我们有:P(T∣S)=0.99
P ( S ) = 0.01 P(S) = 0.01 P(S)=0.01
P ( T ) = P ( T ∣ S ) P ( S ) + P ( T ∣ S ‾ ) P ( S ‾ ) P(T) = P(T|S)P(S) + P(T|\overline{S})P(\overline{S}) P(T)=P(T∣S)P(S)+P(T∣S)P(S)
其中, S ‾ 表示患者不生病。 其中,\overline{S}表示患者不生病。 其中,S表示患者不生病。
根据测试的可靠性,我们可以得到 P ( T ∣ S ‾ ) = 1 − P ( T ∣ S ) = 0.01 因此 P ( T ) = P ( T ∣ S ) P ( S ) + P ( T ∣ S ‾ ) P ( S ‾ ) = ( 0.99 ) ( 0.01 ) + ( 0.01 ) ( 0.99 ) = 0.0198 根据测试的可靠性,我们可以得到 \\P(T|\overline{S}) = 1-P(T|S)= 0.01 \\{}\\因此\\{}\\ \begin{aligned} P(T) &= P(T|S)P(S) + P(T|\overline{S})P(\overline{S}) \\ &= (0.99)(0.01) + (0.01)(0.99) \\ &= 0.0198 \\ \end{aligned} 根据测试的可靠性,我们可以得到P(T∣S)=1−P(T∣S)=0.01因此P(T)=P(T∣S)P(S)+P(T∣S)P(S)=(0.99)(0.01)+(0.01)(0.99)=0.0198
代入贝叶斯公式,我们可以计算出患者生病的条件概率: P ( S ∣ T ) = ( 0.99 ) ( 0.01 ) 0.0198 ≈ 0.50 因此,测试结果为阳性的患者生病的概率约为 50 代入贝叶斯公式,我们可以计算出患者生病的条件概率:\\{}\\P(S|T) = \frac{(0.99)(0.01)}{0.0198} \approx 0.50\\{}\\因此,测试结果为阳性的患者生病的概率约为50%。 代入贝叶斯公式,我们可以计算出患者生病的条件概率:P(S∣T)=0.0198(0.99)(0.01)≈0.50因此,测试结果为阳性的患者生病的概率约为50
使用贝叶斯规则:合并证据


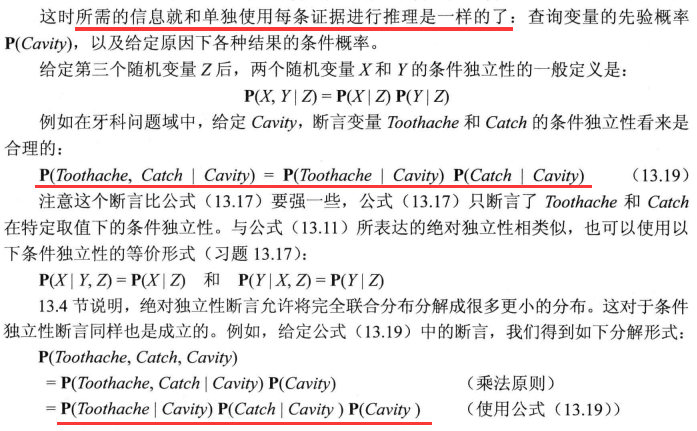
朴素贝叶斯

最大似然估计
最大似然估计(Maximum Likelihood Estimation,简称MLE)是一种常用的参数估计方法,用于根据已知的样本数据来估计模型的参数。它的核心思想是选择能够使观测到的数据出现的概率最大的参数作为估计值。
具体来说,在最大似然估计中,我们假设样本数据来自于某个概率分布,但是该分布的参数是未知的。我们的目标是通过样本数据来估计这些参数,使得该分布能够最好地解释观测到的数据。
假设我们有一个样本集合 X = x 1 , x 2 , . . . , x n X={x_1, x_2, ..., x_n} X=x1,x2,...,xn,每个样本都是来自于某个分布 f ( x ∣ θ ) f(x|\theta) f(x∣θ) 的观测值,其中 θ \theta θ 是分布的参数。我们要找到能够最大化样本集合 X X X 的联合概率密度函数 L ( X ∣ θ ) L(X|\theta) L(X∣θ) 的参数值 θ \theta θ。这个联合概率密度函数可以表示为:
L ( X ∣ θ ) = ∏ i = 1 n f ( x i ∣ θ ) L(X|\theta) = \prod_{i=1}^n f(x_i|\theta) L(X∣θ)=i=1∏nf(xi∣θ)
我们的目标是找到能够最大化 L ( X ∣ θ ) L(X|\theta) L(X∣θ) 的 θ \theta θ 值。因此,最大似然估计的计算可以表示为:
θ ^ M L E = arg max θ L ( X ∣ θ ) \hat{\theta}_{MLE} = \arg\max_{\theta} L(X|\theta) θ^MLE=argθmaxL(X∣θ)
有时候我们需要对上式取对数来避免计算机计算下溢,得到的式子为:
θ ^ M L E = arg max θ log L ( X ∣ θ ) = arg max θ ∑ i = 1 n log f ( x i ∣ θ ) \hat{\theta}_{MLE} = \arg\max_{\theta} \log L(X|\theta) = \arg\max_{\theta} \sum_{i=1}^n \log f(x_i|\theta) θ^MLE=argθmaxlogL(X∣θ)=argθmaxi=1∑nlogf(xi∣θ)
最大似然估计方法是一种常用的参数估计方法,具有计算简单、理论基础好等优点。它在统计学、机器学习、信号处理等领域都得到了广泛应用。
小结
以下是对概率论中重要的公式的整理:
- 条件概率公式:
对于事件 A 和事件 B,其条件概率表示为 P ( A ∣ B ) P(A|B) P(A∣B),表示在事件 B 发生的条件下,事件 A 发生的概率。条件概率公式为:
P ( A ∣ B ) = P ( A , B ) P ( B ) P(A|B) = \frac{P(A,B)}{P(B)} P(A∣B)=P(B)P(A,B)
- 乘法规则公式:
对于事件 A 和事件 B,其联合概率表示为 P ( A , B ) P(A,B) P(A,B),表示事件 A 和事件 B 同时发生的概率。乘法规则公式为:
P ( A , B ) = P ( A ∣ B ) P ( B ) P(A,B) = P(A|B)P(B) P(A,B)=P(A∣B)P(B)
- 链式规则公式:
对于多个事件 A , B , C , D A,B,C,D A,B,C,D,其联合概率表示为 P ( A , B , C , D ) P(A,B,C,D) P(A,B,C,D),链式规则公式可以表示为:
P ( A , B , C , D ) = P ( A ∣ B , C , D ) P ( B ∣ C , D ) P ( C ∣ D ) P ( D ) P(A,B,C,D) = P(A|B,C,D)P(B|C,D)P(C|D)P(D) P(A,B,C,D)=P(A∣B,C,D)P(B∣C,D)P(C∣D)P(D)
- 条件化的链式规则公式:
对于事件 A 和事件 B,其联合概率表示为 P ( A , B ) P(A,B) P(A,B),条件化的链式规则公式可以表示为:
P ( A , B ∣ C ) = P ( A ∣ B , C ) P ( B ∣ C ) P(A,B|C) = P(A|B,C)P(B|C) P(A,B∣C)=P(A∣B,C)P(B∣C)
P ( A , B ∣ C ) P ( C ) = P ( A , B , C ) P ( A ∣ B , C ) P ( B ∣ C ) P ( B , C ) P ( B ∣ C ) = P ( A , B , C ) P(A,B|C) = P ( A ∣ B , C ) P ( B ∣ C ) P ( B , C ) P ( B ∣ C ) P ( C ) = P ( A ∣ B , C ) P ( B ∣ C ) P ( B ∣ C ) P ( B ∣ C ) = P(A|B,C)P(B|C) P(A,B|C)P(C)=P(A,B,C) \\{} \\ \frac{P(A|B,C)P(B|C)P(B,C)}{P(B|C)}=P(A,B,C) \\{} \\ \textbf{P(A,B|C)} = \frac{P(A|B,C)P(B|C)P(B,C)}{P(B|C)P(C)} \\{} \\= \frac{P(A|B,C)P(B|C)P(B|C)}{P(B|C)}=\textbf{P(A|B,C)P(B|C)} P(A,B∣C)P(C)=P(A,B,C)P(B∣C)P(A∣B,C)P(B∣C)P(B,C)=P(A,B,C)P(A,B|C)=P(B∣C)P(C)P(A∣B,C)P(B∣C)P(B,C)=P(B∣C)P(A∣B,C)P(B∣C)P(B∣C)=P(A|B,C)P(B|C)
- 贝叶斯定理公式:
贝叶斯定理是根据先验概率和条件概率来计算后验概率的一种方法,可以用于分类、预测等任务。贝叶斯定理公式为:
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B) = \frac{P(B|A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
- 条件化的贝叶斯定理公式:
对于事件 A 和事件 B,条件化的贝叶斯定理公式可以表示为:
P ( A ∣ B , C ) = P ( B ∣ A , C ) P ( A ∣ C ) P ( B ∣ C ) P(A|B,C) = \frac{P(B|A,C)P(A|C)}{P(B|C)} P(A∣B,C)=P(B∣C)P(B∣A,C)P(A∣C)
- 加法/条件概率公式:
对于事件 A 和事件 B,加法/条件概率公式可以表示为:
P ( A ) = P ( A , B ) + P ( A , ¬ B ) = P ( A ∣ B ) P ( B ) + P ( A ∣ ¬ B ) P ( ¬ B ) P(A) = P(A,B) + P(A,\neg B) = P(A|B)P(B) + P(A|\neg B)P(\neg B) P(A)=P(A,B)+P(A,¬B)=P(A∣B)P(B)+P(A∣¬B)P(¬B)
这些公式在概率论中非常重要,可以应用于统计学、机器学习、信号处理、金融领域、医学领域等各个领域的问题中。熟练掌握这些公式可以帮助我们更好地理解和解决实际问题。
相关文章:

【人工智能】—_不确定性、先验概率_后验概率、概率密度、贝叶斯法则、朴素贝叶斯_、最大似然估计
【人工智能】— 不确定性、先验概率/后验概率、概率密度、贝叶斯法则、朴素贝叶斯 文章目录 【人工智能】— 不确定性、先验概率/后验概率、概率密度、贝叶斯法则、朴素贝叶斯不确定性不确定性与理性决策基本概率符号先验概率(无条件概率)/后验概率(条件概率)随机变量概率密度联…...

postgresql-字符函数
postgresql-字符函数 字符串连接字符与编码字符串长度大小写转换子串查找与替换截断与填充字符串格式化MD5 值字符串拆分字符串反转 字符串连接 concat(str, …)函数用于连接字符串,并且忽略其中的 NULL 参数;concat_ws(sep, str, …) 函数使用指定分隔…...
网络通信)
VUE笔记(五)网络通信
一、axios的简介 1、什么是axios 文档:Axios 中文文档 | Axios 中文网 | Axios 是一个基于 promise 的网络请求库,可以用于浏览器和 node.js 概念:axios是一个基于Promise的网络请求库,可以用于浏览器和node.js 特点ÿ…...

微信小程序修改数据,input不能实时回显
场景: 填写发票抬头,填写抬头公司时候,会根据用户输入的内容实时获取相关的公司信息,用户选择搜索出来的公司,这时候 setData,但是数据并没有回显,而是需要再需要点一下屏幕。 解决方案: 原来…...
GitHub Copilot三连更:能在代码行里直接提问,上下文范围扩展到终端
量子位 | 公众号 QbitAI 就在昨晚,GitHub Copilot迎来了一波不小的更新。 包括: 全新交互体验——代码行中直接召唤聊天功能,不用切界面,主打一个专注; 改善斜杠命令,一键删除,主打快捷操作、…...
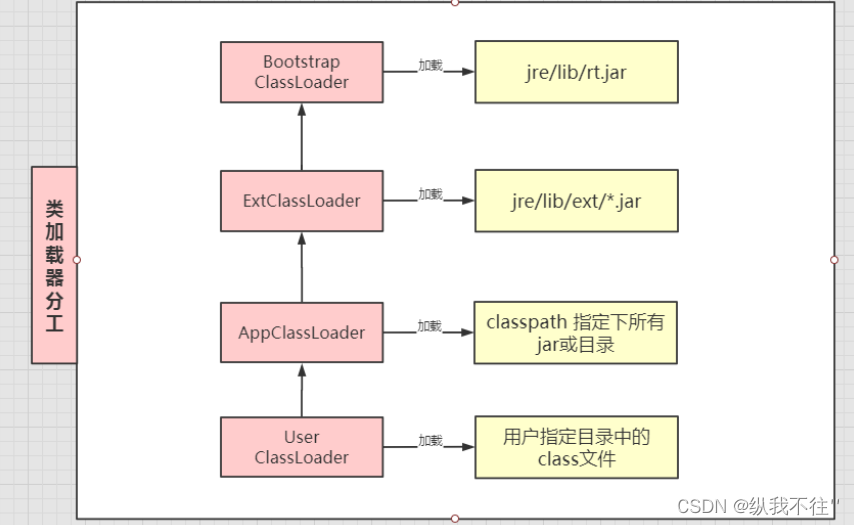
双亲委派机制
双亲委派机制流程 当Application ClassLoader 收到一个类加载请求时,他首先不会自己去尝试加载这个类,而是将这个请求委派给父类加载器Extension ClassLoader去完成。 当Extension ClassLoader收到一个类加载请求时,他首先也不会自己去尝试…...

美团北极星榜单,服务零售的医美新样本
事实证明,任何时候,人们对美的追求都是刚需,只是有时候被压抑了。 德勤中国的《中国医美行业2023年度洞悉报告》(以下简称“报告”)显示,中国医美市场规模预计在2023年超过2000亿元,实现20%增速…...
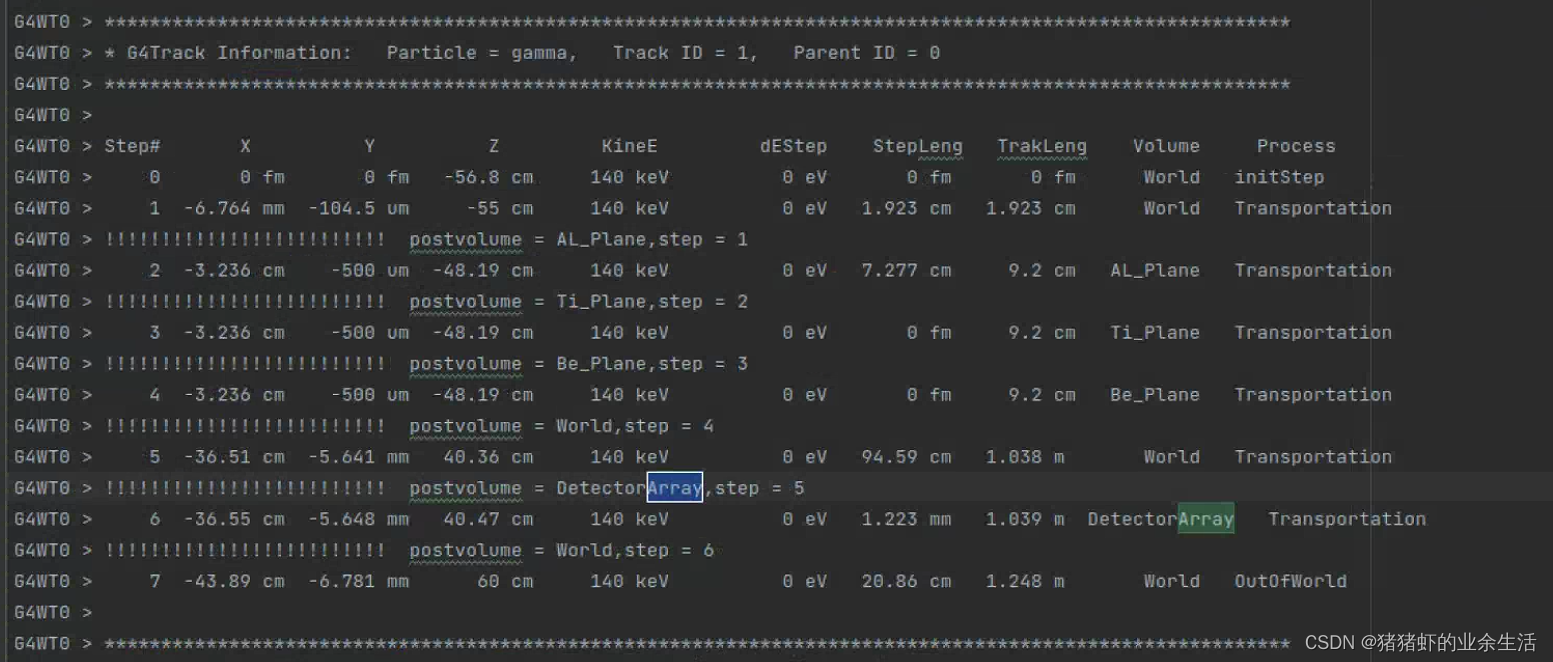
geant4 常用代码
1 获取特特定能量范围的特定粒子 E:\examples_understanding\geant4-v11.0.0_note\examples\extended\runAndEvent\RE02 //-- Particle with kinetic energy filter.G4SDParticleWithEnergyFilter* pkinEFilter new G4SDParticleWithEnergyFilter(fltName"gammaE filter&…...

重要通知!eBay将升级买家满意度考核,如何让你的店铺脱颖而出?
8月份,eBay发布了重要通知,为促进跨境卖家积极提升买家体验,升级了针对卖家的买家满意度考核。其中,产品质量是买家满意度考核的核心,是中国卖家急需提升的重中之重,也是eBay考核的重点。 eBay将着眼于产品…...

PHP中pack、unpack的用法
pack string pack ( string $format [, mixed $args [, mixed $... ]] ) 该函数用来将对应的参数($args)打包成二进制字符串。 其中第一个参数$format,有如下选项: a 以NUL字节填充字符串空白 A 以SPACE(空格)填充字符串 h 十六进制字符串&…...
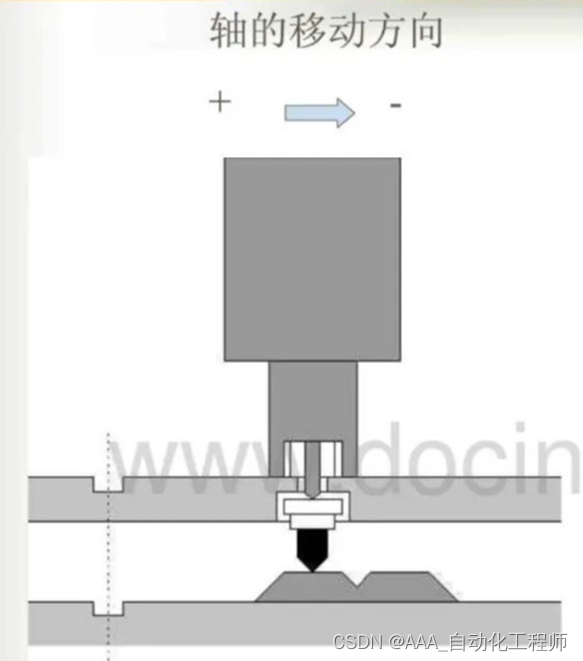
KUKA机器人零点标定的具体方法
KUKA机器人零点标定的具体方法 在进行机器人校正时,先将各轴置于一个定义好的机械位置,即所谓的机械零点。这个机械零点位置表明了同轴的驱动角度之间的对应关系,它用一个测量刻槽表示。 为了精确地确定机器人某根轴的机械零点位置,一般应先找到其预校正位置,然后去掉测量…...
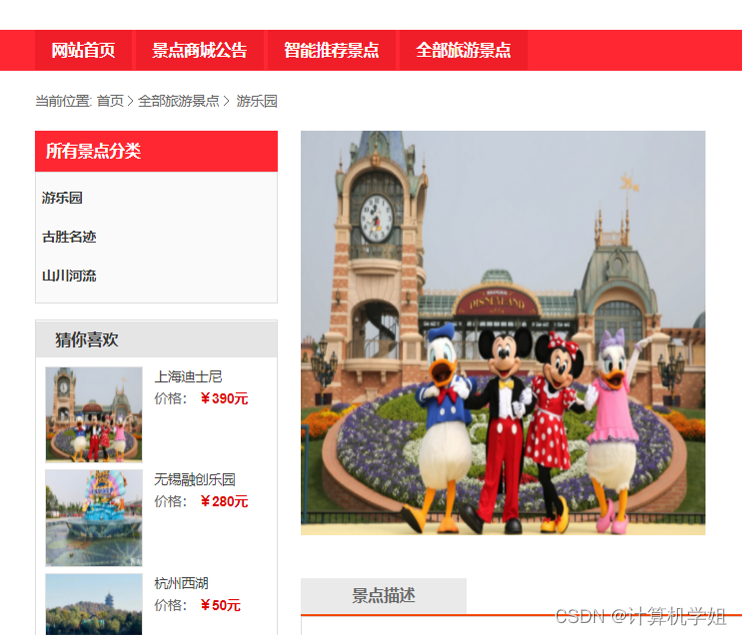
基于SpringBoot+Vue的旅游系统
摘 要 随着旅游业的发展,越来越多的人选择旅游作为自己的出行方式。在旅游规划过程中,旅游景点选择是至关重要的环节。本文提出了一种基于协同过滤推荐算法的旅游平台系统。该系统采用前后端分离的设计,主要使用了SpringBoot、Vue等技术&…...

leetcode算法题--复杂链表的复制
原题链接:https://leetcode.cn/problems/fu-za-lian-biao-de-fu-zhi-lcof/description/?envTypestudy-plan-v2&envIdcoding-interviews 感觉一开始想到的办法还是比较笨 /*** Definition for a Node.* type Node struct {* Val int* Next *Node* …...
C++面试题(叁)---操作系统篇
目录 操作系统篇 1 Linux中查看进程运行状态的指令、查看内存使用情况的指令、 tar解压文件的参数。 2 文件权限怎么修改 3 说说常用的Linux命令 4 说说如何以root权限运行某个程序。 5 说说软链接和硬链接的区别。 6 说说静态库和动态库怎么制作及如何使用,区…...
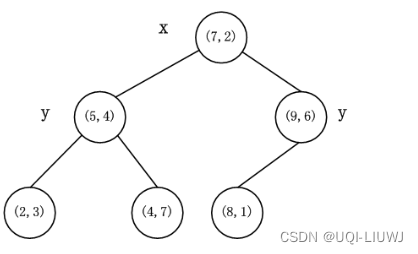
算法笔记:KD树
1 引入原因 K近邻算法需要在整个数据集中搜索和测试数据x最近的k个点,如果一一计算,然后再排序,开销过大 引入KD树的作用就是对KNN搜索和排序的耗时进行改进 2 KD树 2.1 主体思路 以空间换时间,利用训练样本集中的样本点&…...
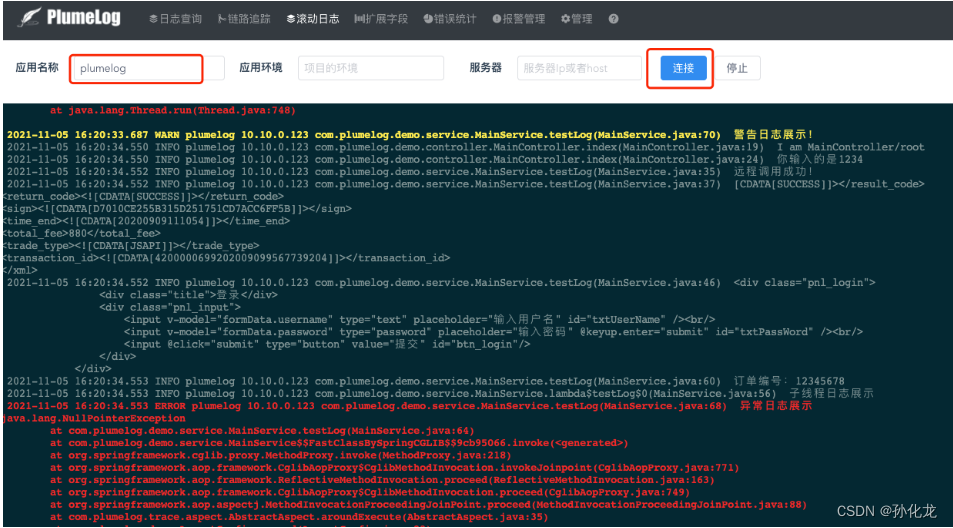
plumelog介绍与应用-一个简单易用的java分布式日志系统
官方文档:http://www.plumelog.com/zh-cn/docs/FASTSTART.html 简介 无代码入侵的分布式日志系统,基于log4j、log4j2、logback搜集日志,设置链路ID,方便查询关联日志基于elasticsearch作为查询引擎高吞吐,查询效率高全…...

百度网盘删除“我的应用数据”文件夹
百度网盘删除“我的应用数据”文件夹电脑端方法-2023.2.27成功 - 哔哩哔哩 (bilibili.com) 百度网盘怎样删除我的应用数据文件夹-手机端方法-2023.3.24日成功 - 哔哩哔哩 (bilibili.com)...

多店铺智能客服,助力店铺销量倍增
近年来电商发展得非常快速,市场竞争也是愈发激烈了。商家不仅需要提高产品和服务的质量,还要争取为自己获取更多的曝光,以此来分散运营的风险和降低经营的成本,所以越来越多的商家也开始转向多平台多店铺运营。但即使运营多个平台…...

会话跟踪技术
cookie 是通过在浏览器第一次请求服务器时,在响应中放入cookie,浏览器接收到cookie后保存在本地,之后每次请求服务器时都将cookie携带到请求头中,用来验证用户身份与状态等。 缺点: 移动端app没有cookiecookie保存在…...
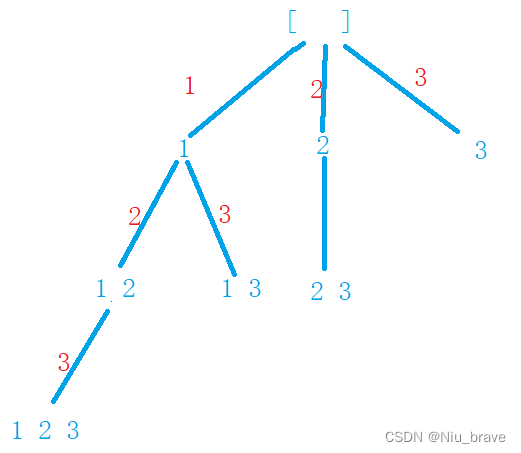
递归算法学习——子集
目录 一,题目解析 二,例子 三,题目接口 四,解题思路以及代码 1.完全深度搜索 2.广度搜索加上深度优先搜索 五,相似题 1.题目 2.题目接口 3.解题代码 一,题目解析 给你一个整数数组 nums ,…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

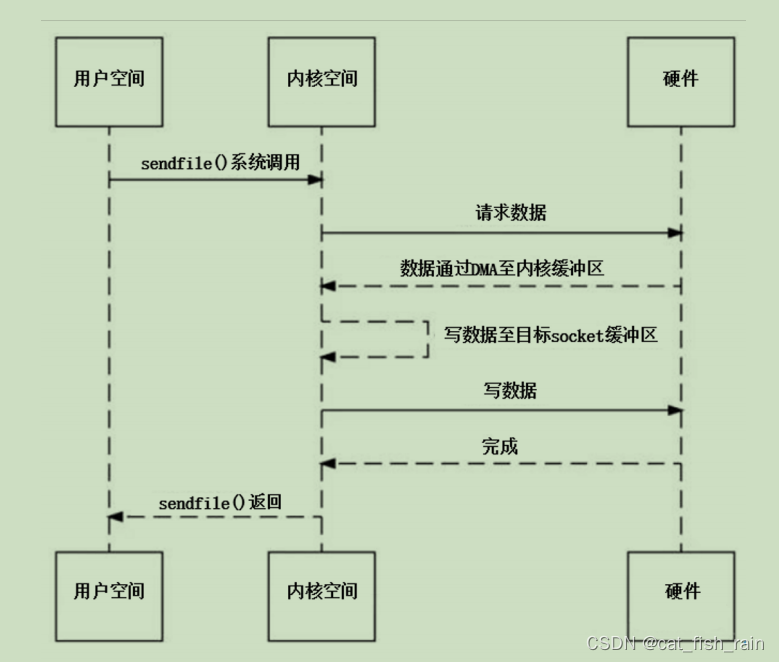
DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...
