为什么建议同时学多门编程语言
晨读一本名叫《4点起床》的书,书中有一段描述与最近学习编制语言时自己的感受完全一致。算是一个小经验,分享给大家。
书中有一章的标题为《同时学六国语言记起来比较快》,其中有两段描述如下:
为什么我推荐大家同时学不同的语言呢?实不相瞒,我这几年在学西班牙语时发现,在学英语的时候,如果你脑子里能有些关于其他外语的知识,掌握语言的速度会变快许多。
西班牙语和英语看似风马牛不相及,其实两者还是很相似的。比如“重要”,在英语里是“important”,西班牙语也是“important”,只是念法不一样罢了。
看到这里,感觉跟自己学习编程语言的感觉完全一致。Java语言用了十多年了,因为工作需要,快速学习了Python和Golang,并精专Golang学习。在学习的过程中,最大的收获不是学会了Golang这门编程语言,而是对Java的编程有了更深入的理解。不仅如此,对整个软件编程都有了更进一步的理解。
举例讲几个方面:
第一,在Java中,我们常用ArrayList来存储一些列数据,而在Golang中常用slice来存储一系列数据。在Java和Golang中,都存在数组,但基本上都很少用数组,而采用列表或切片。而像ArrayList或slice本身又是基于数组来实现的。
对照起来会发现,基本的底层原理都一样,只不过不同语言的实现思路不同而已。
第二,关于HTTP请求。但单纯使用Java进行API请求时,我们往往关注的是API如何使用。当学习多种语言时,你会发现不同的语言有不同的实现形式,但万变不离其宗,都是基于HTTP协议来实现。这样也对HTTP协议本身有了更深入的理解。当然,其他协议也是如此。
第三,关于框架。比如注册中心,在Java中有Nacos、Eureka等实现,而在Golang中,有Consul、Etcd等实现。虽然它们可以跨语言混用,但有了这样横向的对比,对原本语言和框架的学习和掌握更加深刻了。
当然,还有其他许多例子。最根本的是,当你学习了多门语言时,每一个实现都有一个或多个对照,这样对实现的底层就更加理解,而不会过多关注语言本身的语法。不仅拓宽了思路,当有了对照,也能更好理解各自实现的优缺点,以及为什么如此实现。
相关文章:

为什么建议同时学多门编程语言
晨读一本名叫《4点起床》的书,书中有一段描述与最近学习编制语言时自己的感受完全一致。算是一个小经验,分享给大家。 书中有一章的标题为《同时学六国语言记起来比较快》,其中有两段描述如下: 为什么我推荐大家同时学不同的语言…...

langchain agent
zero-shot-react-description 代码 from langchain.agents import initialize_agent from langchain.llms import OpenAI from langchain.tools import BaseTool import os os.environ[OPENAI_API_KEY]"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"# 搜索…...
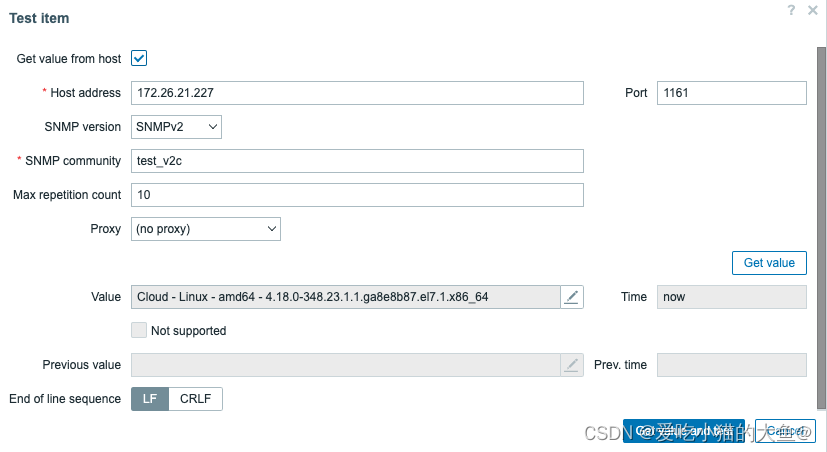
Zabbix下载安装及SNMP Get使用
帮助文档:6. Zabbix Appliance 一、zabbix下载安装 1、获取Zabbix Appliance镜像 Download Zabbix appliance 2、使用该镜像创建虚拟机 3、打开虚拟机控制台自动安装,等待安装完成即可 默认配置 系统/数据库:root:zabbix Zabbix 前端&am…...
freee Programming Contest 2023(AtCoder Beginner Contest 310)
文章目录 A - Order Something Else(模拟)B - Strictly Superior(模拟)C - Reversible(模拟)D - Peaceful Teams(DFS状压)E - NAND repeatedly(普通dp)F - Make 10 Again(状态压缩概率dp&#x…...

恒运资本:概念股是什么意思
概念股是指在特定的经济布景、方针环境、职业远景或社会热点等方面具有某种特别的发展远景和投资价值的股票。在投资者心目中,概念股的危险较大,可是或许带来高于商场平均水平的收益率。那么,概念股到底是什么意思?在本文中&#…...
十九、状态模式
一、什么是状态模式 状态(State)模式的定义:对有状态的对象,把复杂的“判断逻辑”提取到不同的状态对象中,允许状态对象在其内部状态发生改变时改变其行为。 状态模式包含以下主要角色: 环境类(…...
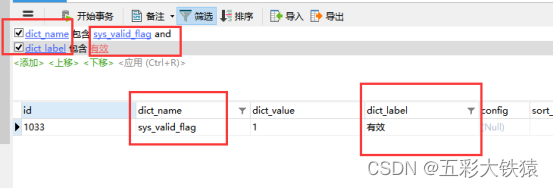
MySQL用navicat工具对表进行筛选查找
这个操作其实很简单,但是对于没操作的人来说,就是不会呀。所以小编出这一个详细图解,希望能够帮助到大家。话不多说看图。 第一步: 点进一张表,点击筛选。 第二步: 点击添加 第三步: 选择要…...

音视频 ffplay简单过滤器
视频旋转 ffplay -i test.mp4 -vf transpose1视频反转 ffplay test.mp4 -vf hflip ffplay test.mp4 -vf vflip视频旋转和反转 ffplay test.mp4 -vf hflip,transpose1音频变速播放 ffplay -i test.mp4 -af atempo2视频变速播放 ffplay -i test.mp4 -vf setptsPTS/2音视频同…...

索引 事务 存储引擎
################索引##################### 一、索引的概念 ●索引是一个排序的列表,在这个列表中存储着索引的值和包含这个值的数据所在行的物理地址(类似于C语言的链表通过指针指向数据记录的内存地址)。 ●使用索引后可以不用扫描全表来…...
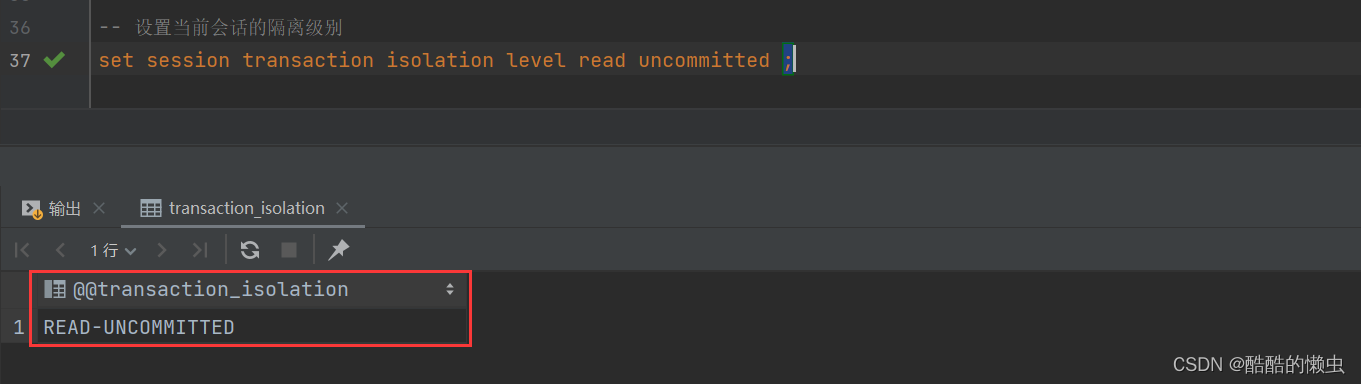
MySQL— 基础语法大全及操作演示!!!(事务)
MySQL—— 基础语法大全及操作演示(事务) 六、事务6.1 事务简介6.2 事务操作6.2.1 未控制事务6.2.2 控制事务一6.2.3 控制事务二 6.3 事务四大特性6.4 并发事务问题6.5 事务隔离级别 MySQL— 基础语法大全及操作演示!!!…...
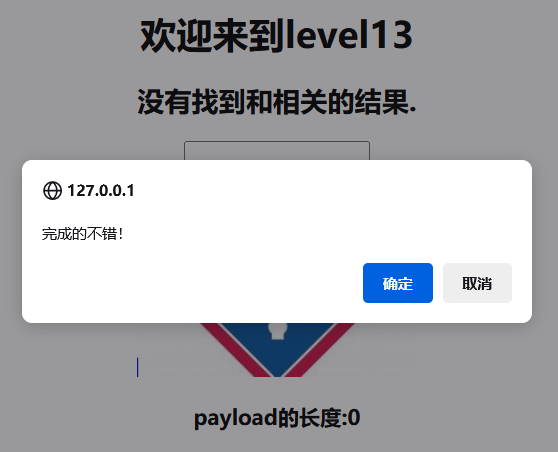
xsschallenge1~13通关详细教程
文章目录 XSS 挑战靶场通关level1level2level3level4level5level6level7level8level9level10level11level12level13 XSS 挑战靶场通关 level1 通过观察发现这个用户信息可以修改 那么我们直接输入攻击代码 <script>alert(/wuhu/)</script>弹框如下: …...

考生作弊行为分析算法
考生作弊行为分析系统利用pythonyolo系列网络模型算法框架,考生作弊行为分析算法利用图像处理和智能算法对考生的行为进行分析和识别,经过算法服务器的复杂计算和逻辑判断,算法将根据考生行为的特征和规律,判定是否存在作弊行为。…...

Python 操作 Redis 数据库介绍
Redis 作为常用的 NoSql 数据库,主要用于缓存数据,提高数据读取效率,那在 Python 中应该如果连接和操作 Redis 呢?今天就为大概简单介绍下,在 Python 中操作 Redis 常用命令。 安装 redis 首先还是需要先安装 redis …...

十年JAVA搬砖路——软件工程概述
软件工程是一门关注软件开发过程的学科,它涉及到软件的设计、开发、测试、部署和维护等方面。软件工程的目标是通过系统化的方法和工具,以确保软件项目能够按时、按预算和按要求完成。 • 软件工程的7个基本概念: 软件生命周期:软…...
前后端项目部署上线详细笔记
部署 参考文章:如何部署网站?来比比谁的方法多 - 哔哩哔哩大家好,我是鱼皮,不知道朋友们有没有试着部署过自己开发的网站呢?其实部署网站非常简单,而且有非常多的花样。这篇文章就给大家分享几种主流的前端…...
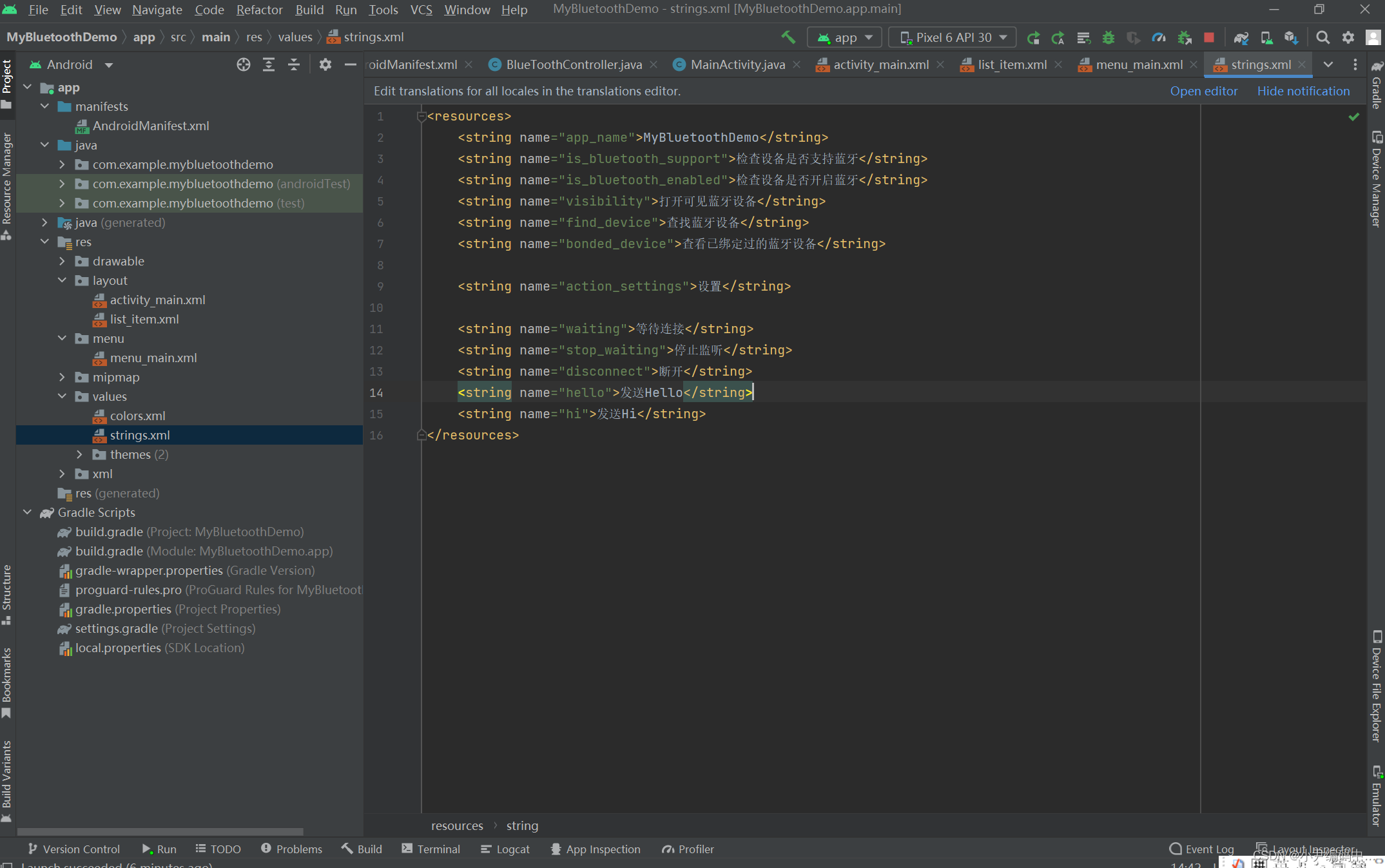
Android 蓝牙开发( 二 )
前言 上一篇文章给大家分享了Android蓝牙的基础知识和基础用法,不过上一篇都是一些零散碎片化的程序,这一篇给大家分享Android蓝牙开发实战项目的初步使用 效果演示 : Android蓝牙搜索,配对,连接,通信 Android蓝牙实…...
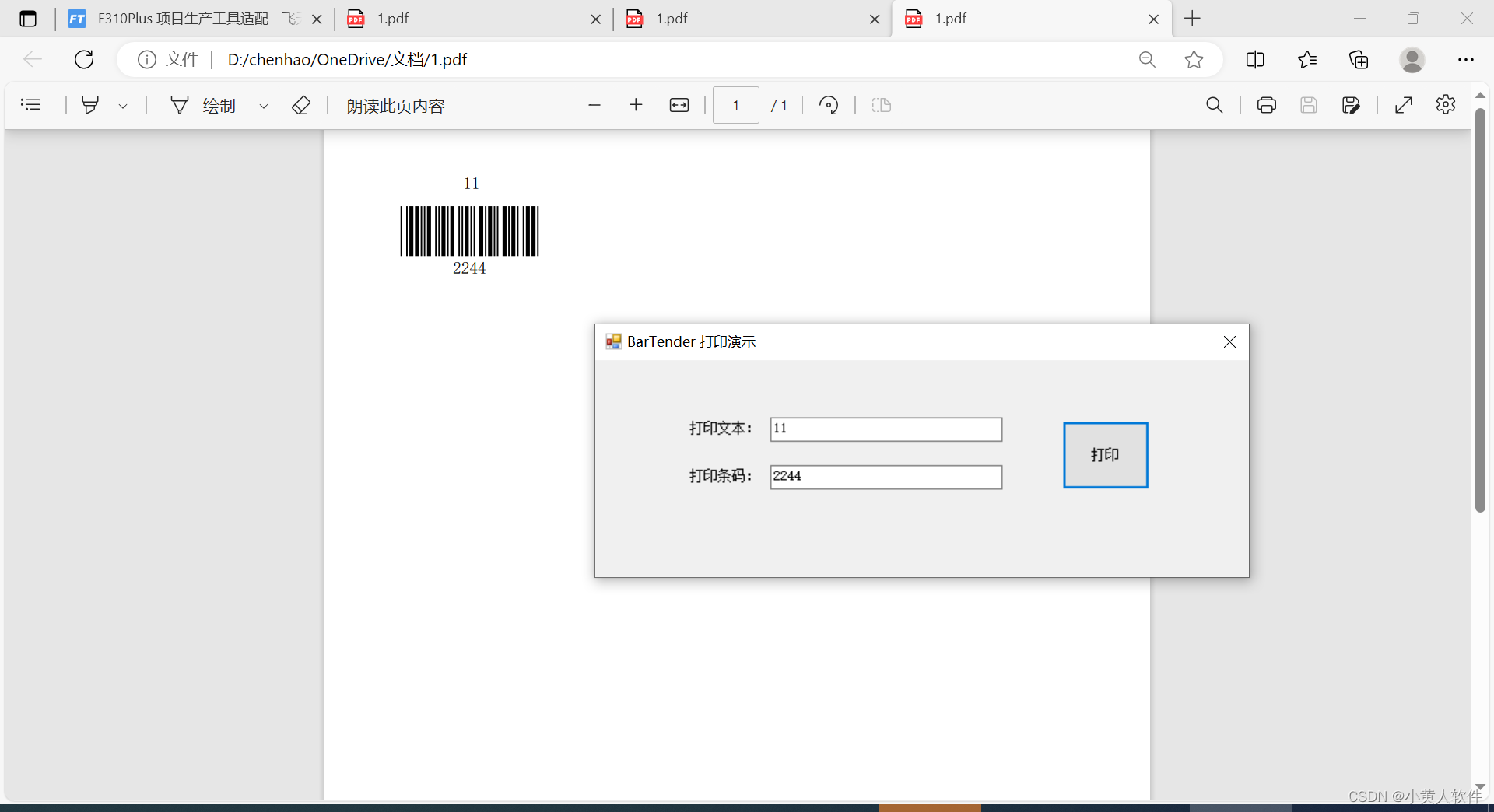
C#调用barTender打印标签示例
使用的电脑需要先安装BarTender 我封装成一个类 using System; using System.Windows.Forms;namespace FT_Tools {public class SysContext{public static BarTender.Application btapp new BarTender.Application();public static BarTender.Format btFormat;public void Q…...
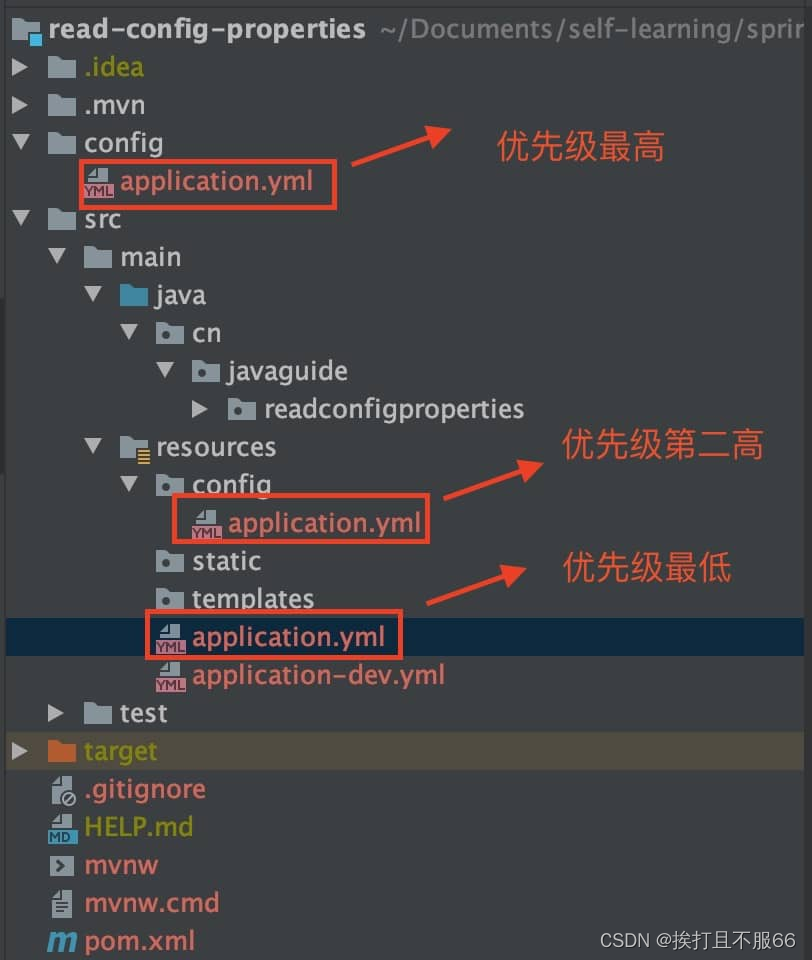
Spring——Spring读取文件
文章目录 1.通过 value 读取比较简单的配置信息2.通过ConfigurationProperties读取并与 bean 绑定3.通过ConfigurationProperties读取并校验4. PropertySource 读取指定 properties 文件5.题外话:Spring加载配置文件的优先级 很多时候我们需要将一些常用的配置信息比如阿里云os…...

这是一条求助贴(postman测试的时候一直是404)
看到这个问题是404的时候总感觉不该求助大家,404多常见一看就是简单的路径问题,我的好像不是,我把我的问题奉上。 首先我先给出我的url http://10.3.22.195:8080/escloud/rest/escloud_contentws/permissionStatistics/jc-haojl/sz 这是我…...
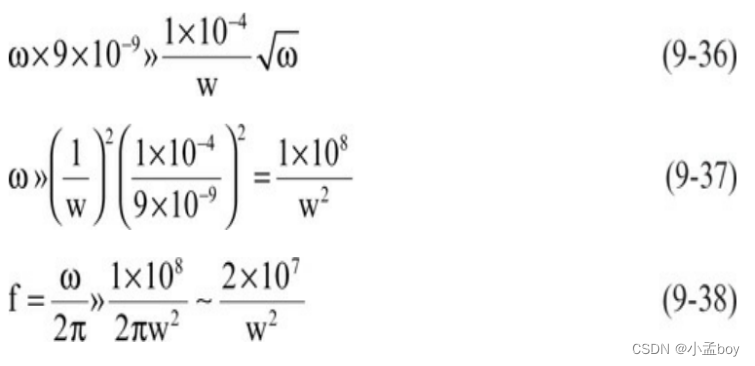
信号完整性分析基础知识之有损传输线、上升时间衰减和材料特性(四):有损传输线建模
传输线中信号衰减的两个损耗过程是通过信号和返回路径导体的串联电阻以及通过有损耗介电材料的分流电阻。这两个电阻器的电阻都与频率相关。 值得注意的是,理想电阻器的电阻随频率恒定。我们已经证明,在理想的有损传输线中,用于描述损耗的两个…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

ubuntu中安装conda的后遗症
缘由: 在编译rk3588的sdk时,遇到编译buildroot失败,提示如下: 提示缺失expect,但是实测相关工具是在的,如下显示: 然后查找借助各个ai工具,重新安装相关的工具,依然无解。 解决&am…...
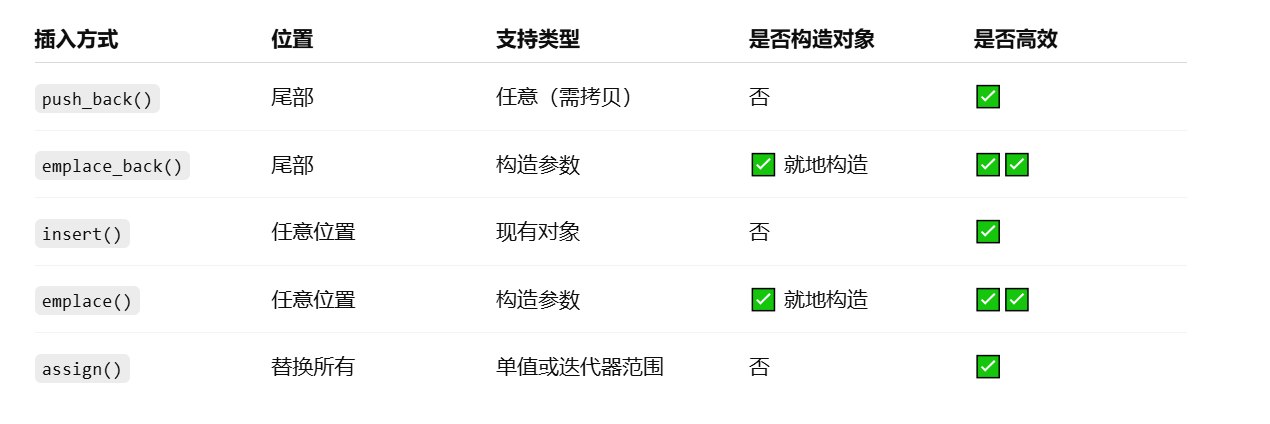
C++中vector类型的介绍和使用
文章目录 一、vector 类型的简介1.1 基本介绍1.2 常见用法示例1.3 常见成员函数简表 二、vector 数据的插入2.1 push_back() —— 在尾部插入一个元素2.2 emplace_back() —— 在尾部“就地”构造对象2.3 insert() —— 在任意位置插入一个或多个元素2.4 emplace() —— 在任意…...
