ransac拟合平面,代替open3d的segment_plane
0.open3d打包太大了,所以决定网上找找代码
使用open3d拟合平面并且求平面的法向量,open3d打包大概1个g的大小。
import open3d as o3dpcd = o3d.geometry.PointCloud()pcd.points = o3d.utility.Vector3dVector(points)## 使用RANSAC算法拟合平面plane_model, inliers = pcd.segment_plane(distance_threshold, ransac_n, num_iterations, probability)plane_normal = np.array(plane_model[:3])plane_normal /= np.linalg.norm(plane_normal)X_normal = [1, 0, 0]Y_normal = [0, 1, 0]Z_normal = [0, 0, 1]# 计算夹角(单位为弧度)angle = np.arccos(np.dot(plane_normal, X_normal))# 将夹角转换为角度X_angel = degrees(angle)# 计算夹角(单位为弧度)angle = np.arccos(np.dot(plane_normal, Y_normal))# 将夹角转换为角度Y_angel = degrees(angle)# 计算夹角(单位为弧度)angle = np.arccos(np.dot(plane_normal, Z_normal))# 将夹角转换为角度Z_angel = degrees(angle)
1.找了一个git上的代码
https://github.com/leomariga/pyRANSAC-3D/blob/master/pyransac3d/plane.py
import randomimport numpy as npclass Plane:"""Implementation of planar RANSAC.Class for Plane object, which finds the equation of a infinite plane using RANSAC algorithim.Call `fit(.)` to randomly take 3 points of pointcloud to verify inliers based on a threshold.---"""def __init__(self):self.inliers = []self.equation = []def fit(self, pts, thresh=0.05, minPoints=100, maxIteration=1000):"""Find the best equation for a plane.:param pts: 3D point cloud as a `np.array (N,3)`.:param thresh: Threshold distance from the plane which is considered inlier.:param maxIteration: Number of maximum iteration which RANSAC will loop over.:returns:- `self.equation`: Parameters of the plane using Ax+By+Cy+D `np.array (1, 4)`- `self.inliers`: points from the dataset considered inliers---"""n_points = pts.shape[0]best_eq = []best_inliers = []for it in range(maxIteration):# Samples 3 random pointsid_samples = random.sample(range(0, n_points), 3)pt_samples = pts[id_samples]# We have to find the plane equation described by those 3 points# We find first 2 vectors that are part of this plane# A = pt2 - pt1# B = pt3 - pt1vecA = pt_samples[1, :] - pt_samples[0, :]vecB = pt_samples[2, :] - pt_samples[0, :]# Now we compute the cross product of vecA and vecB to get vecC which is normal to the planevecC = np.cross(vecA, vecB)# The plane equation will be vecC[0]*x + vecC[1]*y + vecC[0]*z = -k# We have to use a point to find kvecC = vecC / np.linalg.norm(vecC)k = -np.sum(np.multiply(vecC, pt_samples[1, :]))plane_eq = [vecC[0], vecC[1], vecC[2], k]# Distance from a point to a plane# https://mathworld.wolfram.com/Point-PlaneDistance.htmlpt_id_inliers = [] # list of inliers idsdist_pt = (plane_eq[0] * pts[:, 0] + plane_eq[1] * pts[:, 1] + plane_eq[2] * pts[:, 2] + plane_eq[3]) / np.sqrt(plane_eq[0] ** 2 + plane_eq[1] ** 2 + plane_eq[2] ** 2)# Select indexes where distance is biggers than the thresholdpt_id_inliers = np.where(np.abs(dist_pt) <= thresh)[0]if len(pt_id_inliers) > len(best_inliers):best_eq = plane_eqbest_inliers = pt_id_inliersself.inliers = best_inliersself.equation = best_eqreturn self.equation, self.inliers
2.改进代码
2.1 提速
用的时候发现代码的速度比open3d的慢了50ms左右。找了一圈找到方法了
https://zhuanlan.zhihu.com/p/62238520
就是替换循环次数
import randomimport numpy as npclass Plane:"""Implementation of planar RANSAC.Class for Plane object, which finds the equation of a infinite plane using RANSAC algorithim.Call `fit(.)` to randomly take 3 points of pointcloud to verify inliers based on a threshold.---"""def __init__(self):self.inliers = []self.equation = []def fit(self, pts, thresh=0.05, minPoints=100, maxIteration=1000, P=0.99):"""Find the best equation for a plane.:param pts: 3D point cloud as a `np.array (N,3)`.:param thresh: Threshold distance from the plane which is considered inlier.:param maxIteration: Number of maximum iteration which RANSAC will loop over.:param P: desired probability that we get a good sample:returns:- `self.equation`: Parameters of the plane using Ax+By+Cy+D `np.array (1, 4)`- `self.inliers`: points from the dataset considered inliers---"""n_points = pts.shape[0]best_eq = []best_inliers = []i = 0while True:if i < maxIteration:i += 1# Samples 3 random pointsid_samples = random.sample(range(0, n_points), 3)pt_samples = pts[id_samples]# We have to find the plane equation described by those 3 points# We find first 2 vectors that are part of this plane# A = pt2 - pt1# B = pt3 - pt1vecA = pt_samples[1, :] - pt_samples[0, :]vecB = pt_samples[2, :] - pt_samples[0, :]# Now we compute the cross product of vecA and vecB to get vecC which is normal to the planevecC = np.cross(vecA, vecB)# The plane equation will be vecC[0]*x + vecC[1]*y + vecC[0]*z = -k# We have to use a point to find kvecC = vecC / np.linalg.norm(vecC)k = -np.sum(np.multiply(vecC, pt_samples[1, :]))plane_eq = [vecC[0], vecC[1], vecC[2], k]# Distance from a point to a plane# https://mathworld.wolfram.com/Point-PlaneDistance.htmlpt_id_inliers = [] # list of inliers idsdist_pt = (plane_eq[0] * pts[:, 0] + plane_eq[1] * pts[:, 1] + plane_eq[2] * pts[:, 2] +plane_eq[3]) / np.sqrt(plane_eq[0] ** 2 + plane_eq[1] ** 2 + plane_eq[2] ** 2)# Select indexes where distance is biggers than the thresholdpt_id_inliers = np.where(np.abs(dist_pt) <= thresh)[0]#https://www.cse.psu.edu/~rtc12/CSE486/lecture15.pdf#speed upif len(pt_id_inliers) > len(best_inliers):maxIteration = math.log(1 - P) / math.log(1 - pow(len(pt_id_inliers) / n_points, 3))best_eq = plane_eqbest_inliers = pt_id_inliersself.inliers = best_inliersself.equation = best_eqif len(pt_id_inliers) > minPoints:breakreturn self.equation, self.inliers
2.2 提升精度
经过测试发现,拟合的平面的精度还是比open3d差。然后使用最小二乘法在求一次平面了
def ransac_fitplan(pts, thresh=5,num_iterations=1000):# # 希望的得到正确模型的概率n_points = pts.shape[0]best_inliers = []P = 0.9999i=0while True:if i<num_iterations:i+=1# 随机在数据中红选出两个点去求解模型id_samples = random.sample(range(0, n_points), 3)pt_samples = pts[id_samples]vecA = pt_samples[1, :] - pt_samples[0, :]vecB = pt_samples[2, :] - pt_samples[0, :]# Now we compute the cross product of vecA and vecB to get vecC which is normal to the planevecC = np.cross(vecA, vecB)# The plane equation will be vecC[0]*x + vecC[1]*y + vecC[0]*z = -k# We have to use a point to find kvecC = vecC / np.linalg.norm(vecC)k = -np.sum(np.multiply(vecC, pt_samples[1, :]))plane_eq = [vecC[0], vecC[1], vecC[2], k]pt_id_inliers = [] # list of inliers idsdist_pt = (plane_eq[0] * pts[:, 0] + plane_eq[1] * pts[:, 1] + plane_eq[2] * pts[:, 2] + plane_eq[3]) / np.sqrt(plane_eq[0] ** 2 + plane_eq[1] ** 2 + plane_eq[2] ** 2)# Select indexes where distance is biggers than the thresholdpt_id_inliers = np.where(np.abs(dist_pt) <= thresh)[0]if len(pt_id_inliers) > len(best_inliers):num_iterations = math.log(1 - P) / math.log(1 - pow(len(pt_id_inliers) / n_points, 3))best_inliers = pt_id_inliers# 判断是否当前模型已经符合超过一半的点if len(pt_id_inliers) > 0.5*n_points:breakelse:break# 最小二乘法拟合平面X = np.column_stack((pts[:, :2], np.ones(pts.shape[0])))coefficients, _, _, _ = lstsq(X[best_inliers, :], pts[best_inliers, 2])return coefficients,best_inliers
相关文章:

ransac拟合平面,代替open3d的segment_plane
0.open3d打包太大了,所以决定网上找找代码 使用open3d拟合平面并且求平面的法向量,open3d打包大概1个g的大小。 import open3d as o3dpcd o3d.geometry.PointCloud()pcd.points o3d.utility.Vector3dVector(points)## 使用RANSAC算法拟合平面plane_m…...

Docker技术--Docker镜像管理
1.Docker镜像特性 ①.镜像创建容器的特点 Docker在创建容器的时候需要指定镜像,每一个镜像都有唯一的标识:image_id,也可也使用镜像名称和版本号做唯一的标识,如果不指定版本号,那么默认使用的是最新的版本标签(laster)。 ②.镜像分层机制 Docker镜像是分层构建的,并通过…...

生态环境保护3D数字展厅提供了一个线上环保知识学习平台
在21世纪的今天,科技与环保的交汇点提供了无数令人兴奋的可能性。其中,生态环境保护3D数字展厅就是一个绝佳的例子。这个展厅以其独特的3D技术,为我们带来了一个全新的、互动的学习环境,让我们能够更直观地了解和理解我们的环境。…...

OPENCV实现计算描述子
1、计算描述子 kp,des = sift.computer(img,kp) 2、其作用是进行特征匹配 3、同时计算关键点和描述 3.1、kp,des = sift.detectAnd Computer(img,...)...
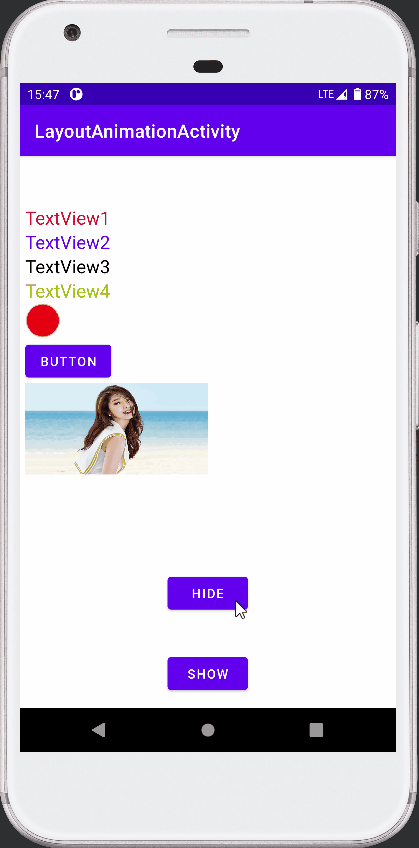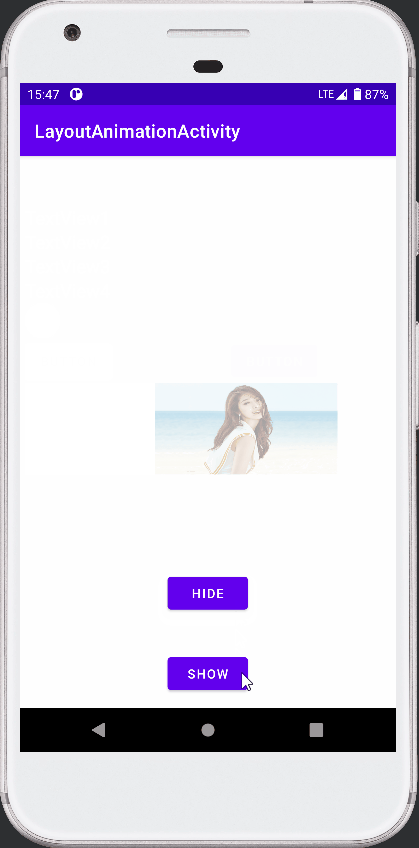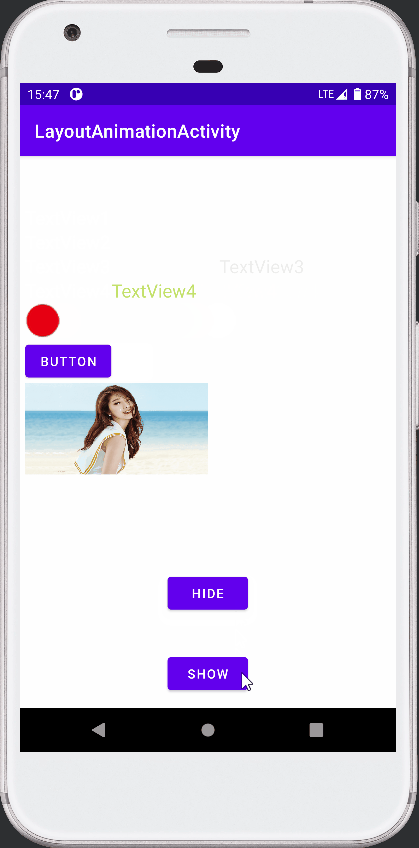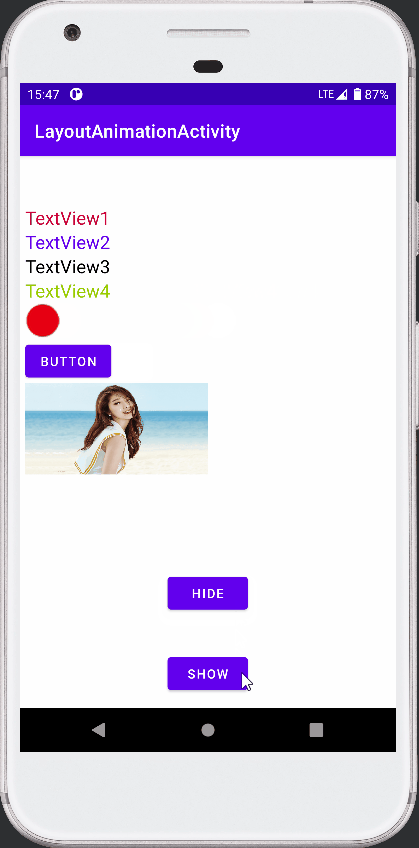
Android View动画之LayoutAnimation的使用
接前篇 Android View动画整理 ,本篇介绍 LayoutAnimation 的使用。 参考《安卓开发艺术探索》。 View 动画作用于 View 。 LayoutAnimation 则作用于 ViewGroup , 为 ViewGoup 指定一个动画,ViewGoup 的子 View 出场时就具体动画效果。 简言…...
低代码与低代码平台的概念解析
随着数字化转型和软件需求的不断增长,传统的手写代码开发方式已经无法满足迅速推出应用程序的需求。为了加快软件开发的速度并降低技术门槛,低代码开发模式应运而生。本文将介绍低代码的概念,探讨什么是低代码什么是低代码平台? 一…...
,及存在的坑)
玩转Mysql系列 - 第8篇:详解排序和分页(order by limit),及存在的坑
这是Mysql系列第7篇。 环境:mysql5.7.25,cmd命令中进行演示。 代码中被[]包含的表示可选,|符号分开的表示可选其一。 本章内容 详解排序查询 详解limit limit存在的坑 分页查询中的坑 排序查询(order by) 电商…...
Django实现音乐网站 ⒂
使用Python Django框架制作一个音乐网站, 本篇主要是歌手详情页-基本信息、单曲列表功能开发实现内容。 目录 歌手基本信息 增加路由 显示视图 模板显示 推荐歌手跳转详情 歌手增加基本信息 表模型增加字段 数据表更新 基本信息增加内容渲染 歌手单曲列表…...
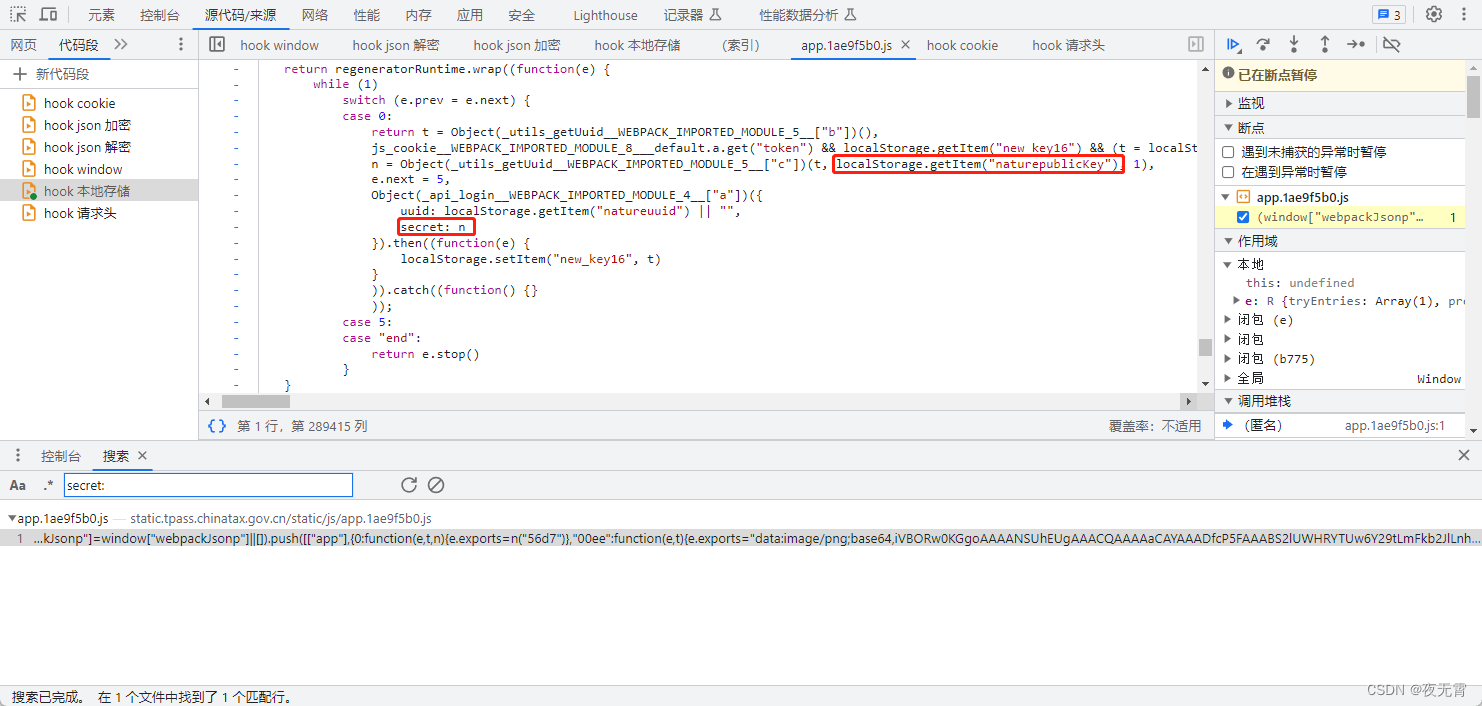
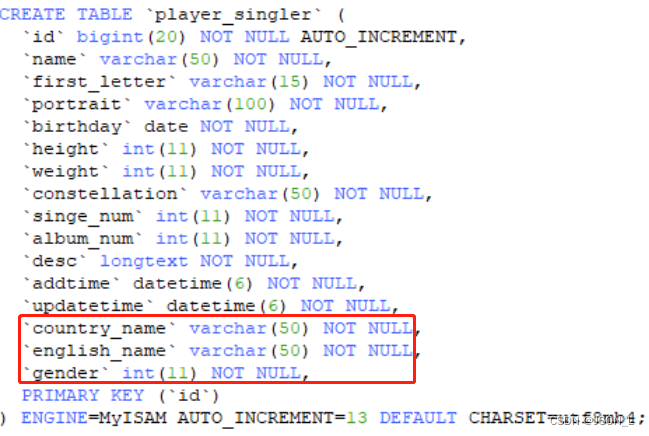
爬虫逆向实战(二十八)--某税网第一步登录
一、数据接口分析 主页地址:某税网 1、抓包 通过抓包可以发现登录接口是factorAccountLogin 2、判断是否有加密参数 请求参数是否加密? 通过查看载荷模块可以发现有一个datagram 和 一个signature加密参数 请求头是否加密? 通过查看“标…...
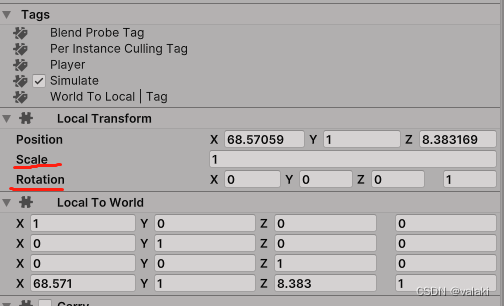
【Dots之003】SystemAPI.Query相关基础笔记
1、SystemAPI.Query 注:SystemAPI.Query只能作为foreach中in的的子句 SystemAPI.Query<RefRO<LocalTransform>>().WithAll<Obstacle>()解析:对于每个具有LocalTransform和Obstacle的Entity;都会将LocalTransform的只读引…...

vue v-for 例子
vue v-for 例子 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title> </head&…...

206.Flink(一):flink概述,flink集群搭建,flink中执行任务,单节点、yarn运行模式,三种部署模式的具体实现
一、Flink概述 1.基本描述 Flink官网地址:Apache Flink — Stateful Computations over Data Streams | Apache Flink Flink是一个框架和分布式处理引擎,用于对无界和有界数据流进行有状态计算。 2.有界流和无界流 无界流(流): 有定义流的开始,没有定义结束。会无休止…...

科技探究之旅--亲子研学活动
2023年8月26日,广州市从化区齐家社会工作服务中心(以下简称“齐家”)的“星乐园-乡村儿童公益辅导服务项目”组织了新开村及西湖村助学点24对亲子到广州市白云区文搏3D打印基地进行“科技探究之旅--亲子研学”活动,旨在发现、点燃…...
华为云Stack的学习(三)
四、华为云Stack公共组件 1.华为云Stack公共负载均衡方案介绍 1.1 LVS原理 LVS是四层负载均衡,建立在OSI模型的传输层之上,所以效率非常高。 LVS有两种转发模式: NAT模式的转发主要通过修改IP地址(位于OSI模型的第三层网络层&…...

大数据平台三大优势详解-行云管家
大数据平台三大优势详解 1、轻松进行数据共享 企业在管理以及快速发展过程中,有着越来越多的数据需要进行管理,如果单独管理则工作量巨大,且难免出现问题,同时共享难。因此需要大数据平台对数据进行统一管理,以及轻松…...

智慧景区方案:AI与视频融合技术如何助力景区监管智能化升级?
随着经济的发展,人们对生活的需求也不再局限于温饱层面,越来越多的人们开始追求文化、艺术的高层次需求,旅游也逐渐成为人们日常放松的一种方式。由于我国人口多、易扎堆等特点,景区的运营监管方式也亟需改革。TSINGSEE青犀智能分…...
HTML基础--Form表单--内联元素
目录 Form表单 表单元素 创建表单 () 文本输入 () 密码输入 单选按钮 () 和 复选框 () 下拉列表 () 和 选项 ()提交按钮 () 重置按钮 () 块元素与行内元素(内联元素) Form表单 HTML中的表单(<form>)是一个重要的元…...

【月度刷题计划同款】常规状压 DP 启发式搜索
题目描述 这是 LeetCode 上的 「1879. 两个数组最小的异或值之和」 ,难度为 「困难」。 Tag : 「状压 DP」、「动态规划」、「启发式搜索」 给你两个整数数组 nums1 和 nums2,它们长度都为 n。 两个数组的 异或值之和 为 (nums1[0] XOR nums2[0]) (nums…...
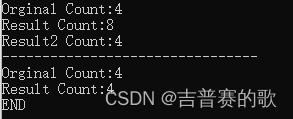
C#: Json序列化和反序列化,集合为什么多出来一些元素?
如下面的例子,很容易看出问题: 如果类本身的无参构造函数, 就添加了一些元素,序列化,再反序列化,会导致元素增加。 如果要避免,必须添加: new JsonSerializerSettings() { Object…...

Docker教程-centos快速安装和配置Docker
# step 1: 安装必要的一些系统工具 sudo yum install -y yum-utils device-mapper-persistent-data lvm2# Step 2: 添加软件源信息 sudo yum-config-manager --add-repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo# Step 3: 更新并安装 Docker-CE sudo …...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
