代码随想录算法训练营第37天 | ● 738.单调递增的数字 ● 968.监控二叉树 ● 总结
文章目录
- 前言
- 一、738.单调递增的数字
- 二、968.监控二叉树
- 总结
前言
可以吗?
一、738.单调递增的数字
本题只要想清楚个例,例如98,一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum[i - 1]减一,strNum[i]赋值9,这样这个整数就是89。就可以很自然想到对应的贪心解法了。
想到了贪心,还要考虑遍历顺序,只有从后向前遍历才能重复利用上次比较的结果。
最后代码实现的时候,也需要一些技巧,例如用一个flag来标记从哪里开始赋值9。
下面代码的flag为start,flag是为了标识使得后面变为9的位置,防止1000得出900的操作(正确:999),亦或是234得出199(正确:234)。
1和2相同,只是更改了length()与length,以及start--->flag;
class Solution {public int monotoneIncreasingDigits(int n) {String s = String.valueOf(n);char[] ch = s.toCharArray();int start = s.length();for(int i = start-1;i>0;i--)if(ch[i-1] > ch[i]){ch[i-1]--;start = i;}for(int i = start;i<s.length();i++){ch[i] = '9';}return Integer.parseInt(String.valueOf(ch));}
}class Solution {public int monotoneIncreasingDigits(int n) {String s = String.valueOf(n);char[] ch = s.toCharArray();int flag = ch.length;for(int i = flag-1;i>0;i--){if(ch[i-1] > ch[i]){ch[i-1]--;flag = i;}}for(int i = flag;i < ch.length;i++){ch[i] = '9';}return Integer.parseInt(String.valueOf(ch));}
}二、968.监控二叉树
从题目中示例,其实可以得到启发,我们发现题目示例中的摄像头都没有放在叶子节点上!这是很重要的一个线索,摄像头可以覆盖上中下三层,如果把摄像头放在叶子节点上,就浪费的一层的覆盖。所以把摄像头放在叶子节点的父节点位置,才能充分利用摄像头的覆盖面积。那么有同学可能问了,为什么不从头结点开始看起呢,为啥要从叶子节点看呢?
因为头结点放不放摄像头也就省下一个摄像头, 叶子节点放不放摄像头省下了的摄像头数量是指数阶别的。所以我们要从下往上看,局部最优:让叶子节点的父节点安摄像头,所用摄像头最少,整体最优:全部摄像头数量所用最少!局部最优推出全局最优,找不出反例,那么就按照贪心来!
此时,大体思路就是从低到上,先给叶子节点父节点放个摄像头,然后隔两个节点放一个摄像头,直至到二叉树头结点。此时这道题目还有两个难点:
- 二叉树的遍历
- 如何隔两个节点放一个摄像头
有如下三种:
- 该节点无覆盖
- 本节点有摄像头
- 本节点有覆盖
我们分别有三个数字来表示:
- 0:该节点无覆盖
- 1:本节点有摄像头
- 2:本节点有覆盖
大家应该找不出第四个节点的状态了。
一些同学可能会想有没有第四种状态:本节点无摄像头,其实无摄像头就是 无覆盖 或者 有覆盖的状态,所以一共还是三个状态。
因为在遍历树的过程中,就会遇到空节点,那么问题来了,空节点究竟是哪一种状态呢? 空节点表示无覆盖? 表示有摄像头?还是有覆盖呢?
空节点不能是无覆盖的状态,这样叶子节点就要放摄像头了,空节点也不能是有摄像头的状态,这样叶子节点的父节点就没有必要放摄像头了,而是可以把摄像头放在叶子节点的爷爷节点上。
所以空节点的状态只能是有覆盖,这样就可以在叶子节点的父节点放摄像头了;
本题的难点首先是要想到贪心的思路,然后就是遍历和状态推导。
在二叉树上进行状态推导,其实难度就上了一个台阶了,需要对二叉树的操作非常娴熟。
/**
节点的状态值:
0 表示无覆盖
1 表示 有摄像头
2 表示有覆盖
后序遍历,根据左右节点的情况,来判读 自己的状态
*/
// 如果左右节点都覆盖了的话, 那么本节点的状态就应该是无覆盖,没有摄像头 (2,2)
// 左右节点都是无覆盖状态,那 根节点此时应该放一个摄像头, (0,0) (0,1) (0,2) (1,0) (2,0),状态值为 1,摄像头数 ++;
// 左右节点的 状态为 (1,1) (1,2) (2,1) 也就是左右节点至少存在 1个摄像头,那么本节点就是处于被覆盖状态
class Solution {int res=0;public int minCameraCover(TreeNode root) {// 对根节点的状态做检验,防止根节点是无覆盖状态 .if(minCame(root)==0){res++;}return res;}/**节点的状态值:0 表示无覆盖1 表示 有摄像头2 表示有覆盖后序遍历,根据左右节点的情况,来判读 自己的状态*/public int minCame(TreeNode root){if(root==null){// 空节点默认为 有覆盖状态,避免在叶子节点上放摄像头return 2;}int left=minCame(root.left);int right=minCame(root.right);// 如果左右节点都覆盖了的话, 那么本节点的状态就应该是无覆盖,没有摄像头if(left==2&&right==2){//(2,2)return 0;}else if(left==0||right==0){// 左右节点都是无覆盖状态,那 根节点此时应该放一个摄像头// (0,0) (0,1) (0,2) (1,0) (2,0)// 状态值为 1 摄像头数 ++;res++;return 1;}else{// 左右节点的 状态为 (1,1) (1,2) (2,1) 也就是左右节点至少存在 1个摄像头,// 那么本节点就是处于被覆盖状态return 2;}}
}
总结
我们可以的!
只要一路坚持下来,不仅基础扎实,而且进步也是飞速的。
相关文章:

代码随想录算法训练营第37天 | ● 738.单调递增的数字 ● 968.监控二叉树 ● 总结
文章目录 前言一、738.单调递增的数字二、968.监控二叉树总结 前言 可以吗? 一、738.单调递增的数字 本题只要想清楚个例,例如98,一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum…...
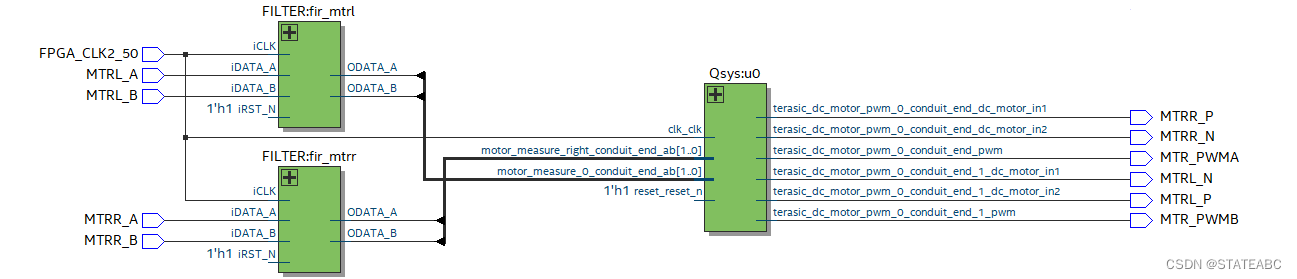
SOPC之NIOS Ⅱ实现电机转速PID控制(调用中断函数)
通过FPGA开发板上的NIOS Ⅱ搭建电机控制的硬件平台,包括电机正反转、编码器的读取,再通过软件部分实现PID算法对电机速度进行控制,使其能够渐近设定的编码器目标值。 一、问题与改进 SOPC之NIOS Ⅱ实现电机转速PID控制_STATEABC的博客-CSDN…...
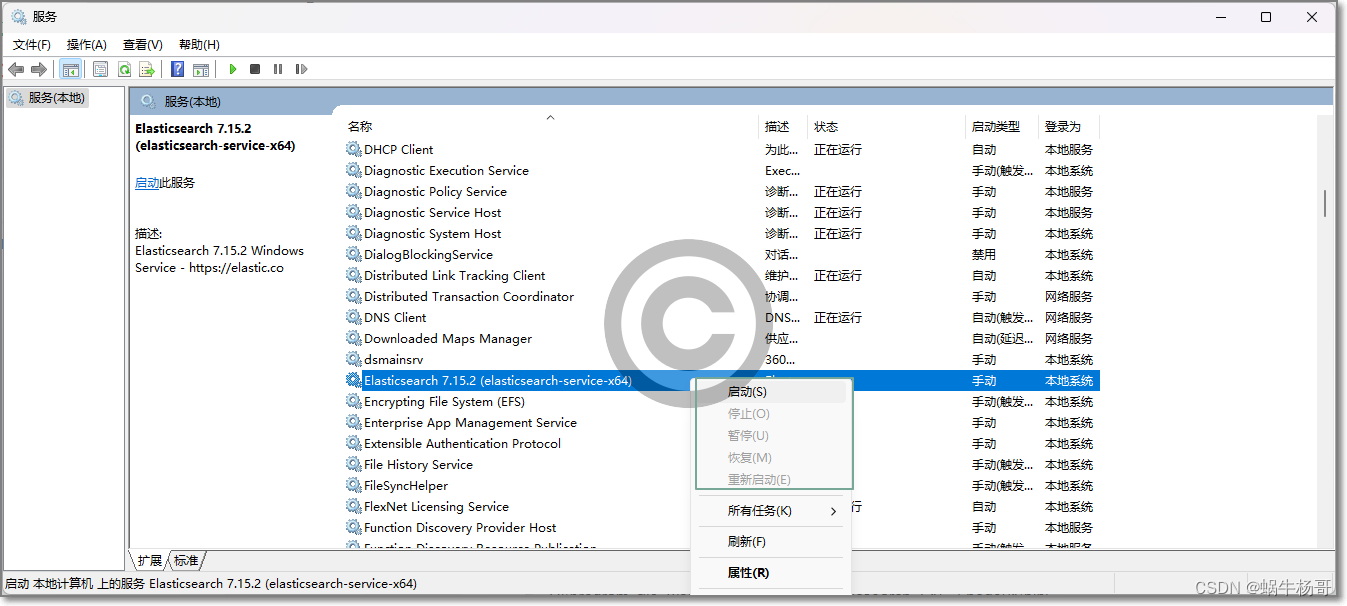
ElasticSearch安装为Win11服务
在windows的环境下操作是Elasticsearch,并且喜欢使用命令行 ,启动时通过cmd直接在elasticsearch的bin目录下执行elasticsearch ,这样直接启动的话集群名称会默elasticsearch,节点名称会随机生成。 停止就直接在cmd界面按CtrlC 其实我们也可以将elasticse…...

ransac拟合平面,代替open3d的segment_plane
0.open3d打包太大了,所以决定网上找找代码 使用open3d拟合平面并且求平面的法向量,open3d打包大概1个g的大小。 import open3d as o3dpcd o3d.geometry.PointCloud()pcd.points o3d.utility.Vector3dVector(points)## 使用RANSAC算法拟合平面plane_m…...

Docker技术--Docker镜像管理
1.Docker镜像特性 ①.镜像创建容器的特点 Docker在创建容器的时候需要指定镜像,每一个镜像都有唯一的标识:image_id,也可也使用镜像名称和版本号做唯一的标识,如果不指定版本号,那么默认使用的是最新的版本标签(laster)。 ②.镜像分层机制 Docker镜像是分层构建的,并通过…...

生态环境保护3D数字展厅提供了一个线上环保知识学习平台
在21世纪的今天,科技与环保的交汇点提供了无数令人兴奋的可能性。其中,生态环境保护3D数字展厅就是一个绝佳的例子。这个展厅以其独特的3D技术,为我们带来了一个全新的、互动的学习环境,让我们能够更直观地了解和理解我们的环境。…...

OPENCV实现计算描述子
1、计算描述子 kp,des = sift.computer(img,kp) 2、其作用是进行特征匹配 3、同时计算关键点和描述 3.1、kp,des = sift.detectAnd Computer(img,...)...
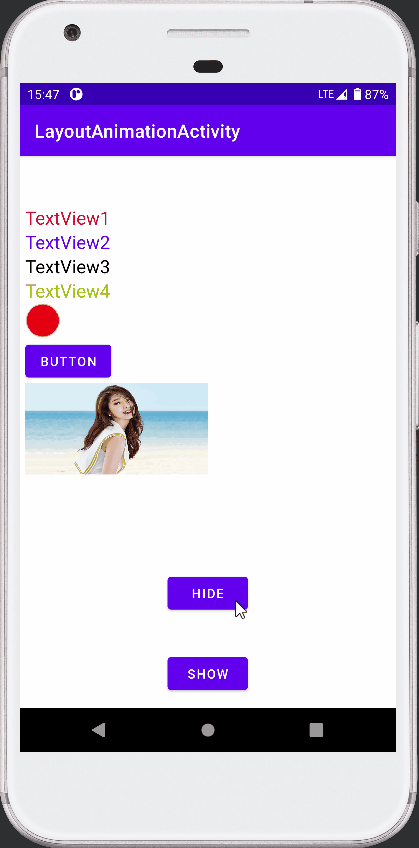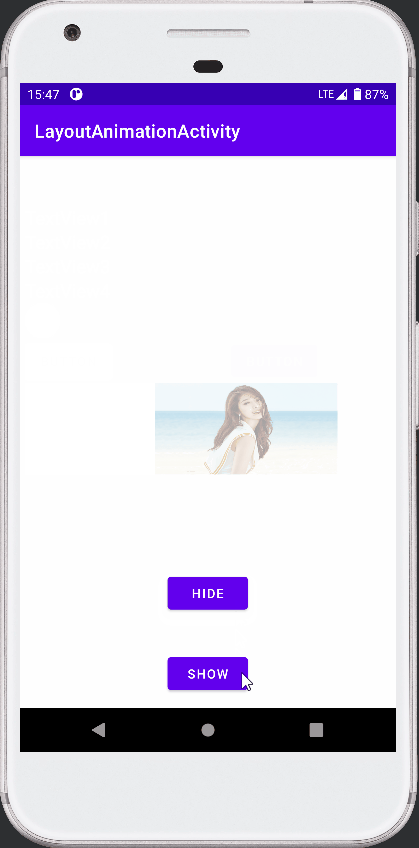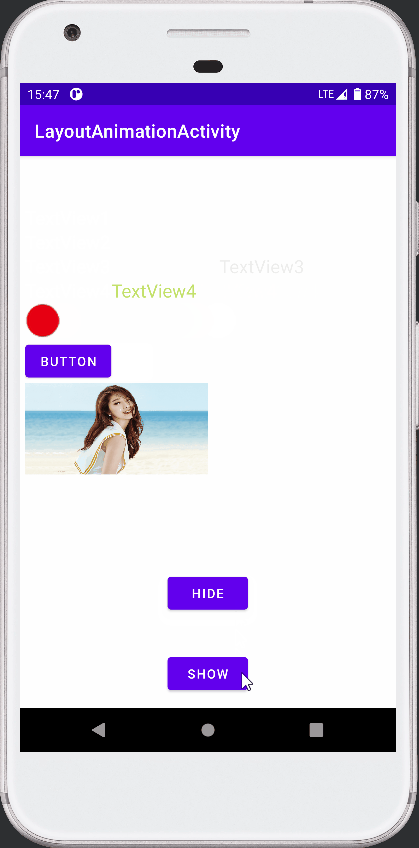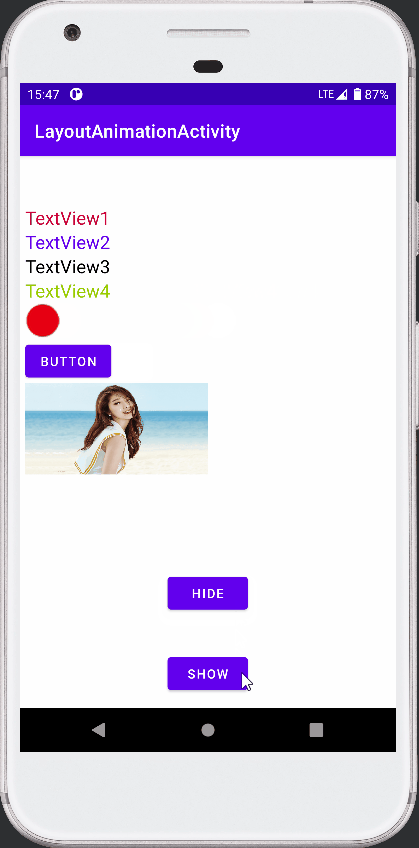
Android View动画之LayoutAnimation的使用
接前篇 Android View动画整理 ,本篇介绍 LayoutAnimation 的使用。 参考《安卓开发艺术探索》。 View 动画作用于 View 。 LayoutAnimation 则作用于 ViewGroup , 为 ViewGoup 指定一个动画,ViewGoup 的子 View 出场时就具体动画效果。 简言…...
低代码与低代码平台的概念解析
随着数字化转型和软件需求的不断增长,传统的手写代码开发方式已经无法满足迅速推出应用程序的需求。为了加快软件开发的速度并降低技术门槛,低代码开发模式应运而生。本文将介绍低代码的概念,探讨什么是低代码什么是低代码平台? 一…...
,及存在的坑)
玩转Mysql系列 - 第8篇:详解排序和分页(order by limit),及存在的坑
这是Mysql系列第7篇。 环境:mysql5.7.25,cmd命令中进行演示。 代码中被[]包含的表示可选,|符号分开的表示可选其一。 本章内容 详解排序查询 详解limit limit存在的坑 分页查询中的坑 排序查询(order by) 电商…...
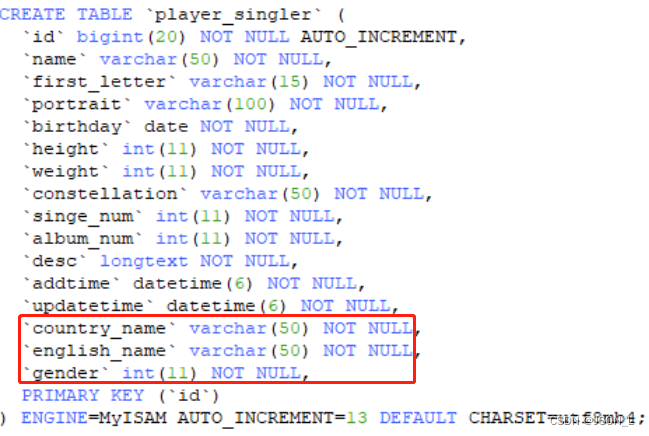
Django实现音乐网站 ⒂
使用Python Django框架制作一个音乐网站, 本篇主要是歌手详情页-基本信息、单曲列表功能开发实现内容。 目录 歌手基本信息 增加路由 显示视图 模板显示 推荐歌手跳转详情 歌手增加基本信息 表模型增加字段 数据表更新 基本信息增加内容渲染 歌手单曲列表…...
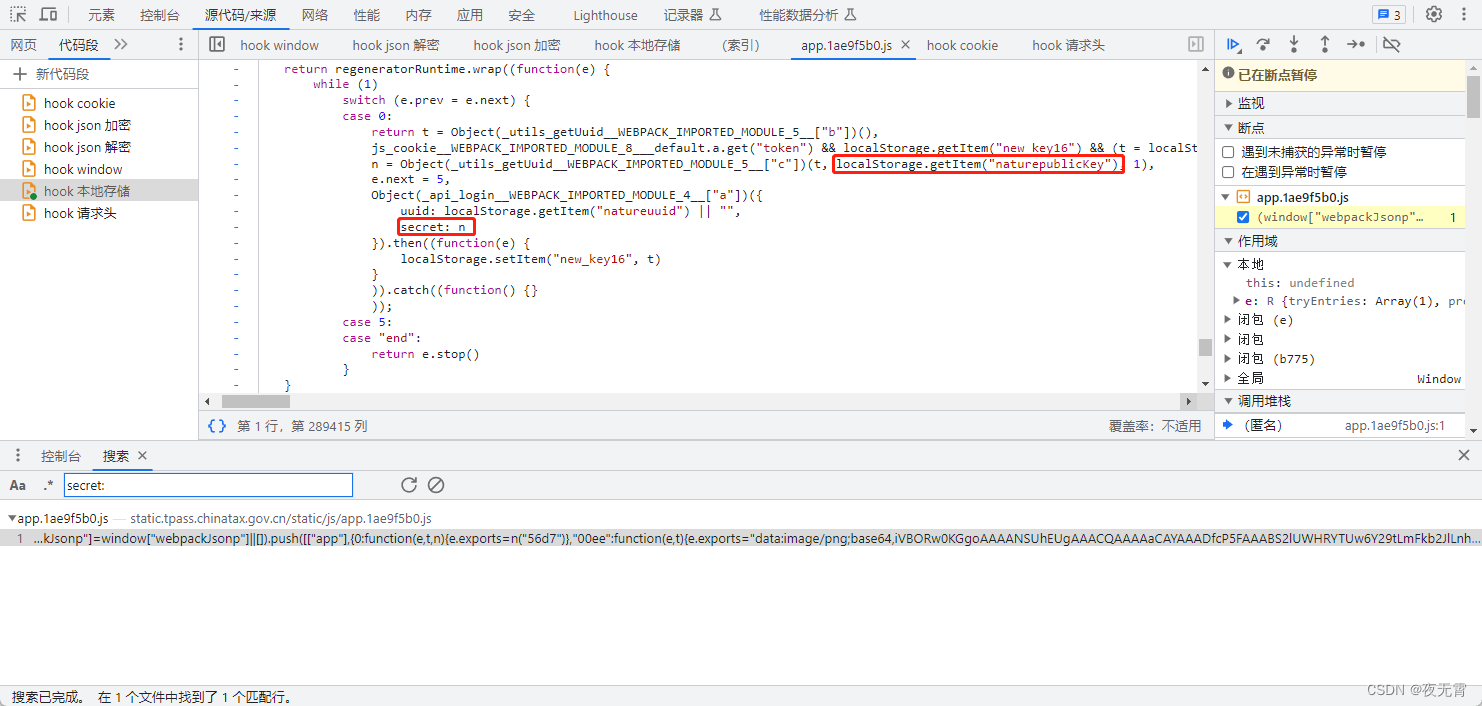
爬虫逆向实战(二十八)--某税网第一步登录
一、数据接口分析 主页地址:某税网 1、抓包 通过抓包可以发现登录接口是factorAccountLogin 2、判断是否有加密参数 请求参数是否加密? 通过查看载荷模块可以发现有一个datagram 和 一个signature加密参数 请求头是否加密? 通过查看“标…...
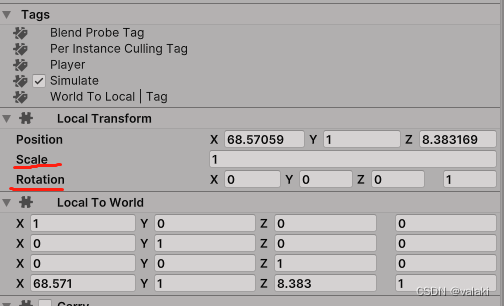
【Dots之003】SystemAPI.Query相关基础笔记
1、SystemAPI.Query 注:SystemAPI.Query只能作为foreach中in的的子句 SystemAPI.Query<RefRO<LocalTransform>>().WithAll<Obstacle>()解析:对于每个具有LocalTransform和Obstacle的Entity;都会将LocalTransform的只读引…...

vue v-for 例子
vue v-for 例子 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title> </head&…...

206.Flink(一):flink概述,flink集群搭建,flink中执行任务,单节点、yarn运行模式,三种部署模式的具体实现
一、Flink概述 1.基本描述 Flink官网地址:Apache Flink — Stateful Computations over Data Streams | Apache Flink Flink是一个框架和分布式处理引擎,用于对无界和有界数据流进行有状态计算。 2.有界流和无界流 无界流(流): 有定义流的开始,没有定义结束。会无休止…...

科技探究之旅--亲子研学活动
2023年8月26日,广州市从化区齐家社会工作服务中心(以下简称“齐家”)的“星乐园-乡村儿童公益辅导服务项目”组织了新开村及西湖村助学点24对亲子到广州市白云区文搏3D打印基地进行“科技探究之旅--亲子研学”活动,旨在发现、点燃…...
华为云Stack的学习(三)
四、华为云Stack公共组件 1.华为云Stack公共负载均衡方案介绍 1.1 LVS原理 LVS是四层负载均衡,建立在OSI模型的传输层之上,所以效率非常高。 LVS有两种转发模式: NAT模式的转发主要通过修改IP地址(位于OSI模型的第三层网络层&…...

大数据平台三大优势详解-行云管家
大数据平台三大优势详解 1、轻松进行数据共享 企业在管理以及快速发展过程中,有着越来越多的数据需要进行管理,如果单独管理则工作量巨大,且难免出现问题,同时共享难。因此需要大数据平台对数据进行统一管理,以及轻松…...

智慧景区方案:AI与视频融合技术如何助力景区监管智能化升级?
随着经济的发展,人们对生活的需求也不再局限于温饱层面,越来越多的人们开始追求文化、艺术的高层次需求,旅游也逐渐成为人们日常放松的一种方式。由于我国人口多、易扎堆等特点,景区的运营监管方式也亟需改革。TSINGSEE青犀智能分…...
HTML基础--Form表单--内联元素
目录 Form表单 表单元素 创建表单 () 文本输入 () 密码输入 单选按钮 () 和 复选框 () 下拉列表 () 和 选项 ()提交按钮 () 重置按钮 () 块元素与行内元素(内联元素) Form表单 HTML中的表单(<form>)是一个重要的元…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
