20230830比赛总结
分数
预估分数: 100 + 100 + [ 0 , 20 ] + 100 = [ 300 , 320 ] 100+100+[0,20]+100=[300,320] 100+100+[0,20]+100=[300,320]
实际分数: 100 + 100 + 10 + 100 = 310 100+100+10+100=310 100+100+10+100=310
反思
B
只是粗略观察表就急于写决策单调性优化,写完后才发现有些位置不单调,以后需要用程序 c h e c k check check,而不是自己肉眼看
C
没想到人类智慧的结论:直径可以衡量树的减少
感觉学到了一个套路
题解
比赛链接
A
不说了,就一个二分 + d f s +dfs +dfs 的事
B
感觉挺套路的,先写一个暴力的 d p dp dp(需要费用提前计算,否则不好优化)
因为有最大最小值,所以用单调栈 + 线段树优化
有一个插曲是我打表转移点,看了前二十个,以为是单调的,然后写了个决策单调性,发现 W A WA WA 了,然后才发现打表中有几个转移点不单调!!!
C
神仙博弈题
考虑树在不断减小的过程中,用什么来衡量减小的量?直径!
可以发现,当直径长度 > 2 >2 >2 时,每次操作可以让直径长度 − 1 -1 −1 或 − 2 -2 −2,考虑问题变成了一堆石子,每次可以取 1 / 2 1/2 1/2 个,求先手必胜还是后手必胜
这就很 e a s y easy easy 了,对于 % 3 \%3 %3 的余数分类讨论即可
现在考虑维护直径,有一个很常用我却想不到 的方法是用线段树
因为直径是可以合并的
考虑到查询的情况只有 3 种不同的
- x = y x=y x=y,即为整棵树的直径
- y y y 是 x x x 的祖先,把 y y y 的包含 x x x 的子树抠掉,即把两段区间合并即可
- 其他情况,与以 1 为根 y y y 的子树相同
树上两点距离用 r m q rmq rmq 即可
时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)
#include <bits/stdc++.h>
using namespace std;
const int N=400100;
int n,q,depth[N],up[N][20],f[N],g[N];
int dfn[N],siz[N],rv[N],dfs_clock;
int eul[N],cnt,fir[N];
int lg[N],st[N][20];
int e[N<<1],h[N],ne[N<<1],idx;
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
void add(int x,int y){ e[idx]=y,ne[idx]=h[x],h[x]=idx++;}
void dfs(int u,int fa){siz[u]=1;dfn[u]=++dfs_clock,rv[dfs_clock]=u;depth[u]=depth[fa]+1,up[u][0]=fa;eul[++cnt]=u,fir[u]=cnt;for(int i=h[u];~i;i=ne[i]){if(e[i]==fa) continue;dfs(e[i],u),eul[++cnt]=u,siz[u]+=siz[e[i]];}
}
int get_lca(int x,int y){x=fir[x],y=fir[y];if(x>y) swap(x,y);int k=lg[y-x+1];return min(st[x][k],st[y-(1<<k)+1][k]);
}
int calc(int x,int y){ return depth[x]+depth[y]-get_lca(x,y)*2+1;}
struct Node{int u,v;
}seg[N<<2];
struct Segment{Node pushup(Node x,Node y){Node ret;ret.u=x.u,ret.v=x.v;if(calc(y.u,y.v)>calc(ret.u,ret.v)) ret.u=y.u,ret.v=y.v;if(calc(x.u,y.u)>calc(ret.u,ret.v)) ret.u=x.u,ret.v=y.u;if(calc(x.u,y.v)>calc(ret.u,ret.v)) ret.u=x.u,ret.v=y.v;if(calc(x.v,y.u)>calc(ret.u,ret.v)) ret.u=x.v,ret.v=y.u;if(calc(x.v,y.v)>calc(ret.u,ret.v)) ret.u=x.v,ret.v=y.v;return ret;}void build(int l,int r,int x){if(l==r){ seg[x].u=seg[x].v=rv[l];return;}int mid=(l+r)>>1;build(l,mid,x<<1),build(mid+1,r,x<<1^1);seg[x]=pushup(seg[x<<1],seg[x<<1^1]);}Node query(int l,int r,int x,int L,int R){if(L<=l&&r<=R) return seg[x];int mid=(l+r)>>1;if(mid>=L&&mid<R) return pushup(query(l,mid,x<<1,L,R),query(mid+1,r,x<<1^1,L,R));if(mid>=L) return query(l,mid,x<<1,L,R);return query(mid+1,r,x<<1^1,L,R);}
}sg;
int get_low_anc(int x,int y){for(int i=19;i>=0;i--) if(depth[up[y][i]]>depth[x]) y=up[y][i];return y;
}
int main(){freopen("fragile.in","r",stdin);freopen("fragile.out","w",stdout);n=read(),q=read();memset(h,-1,sizeof(h));for(int i=1;i<n;i++){int x=read(),y=read();add(x,y),add(y,x);}dfs(1,0);for(int i=2;i<=n<<1;i++) lg[i]=lg[i>>1]+1;// for(int i=1;i<=n<<1;i++) cout<<eul[i]<<' ';cout<<'\n';for(int i=1;i<=n<<1;i++) st[i][0]=depth[eul[i]];for(int j=1;j<20;j++) for(int i=1;i+(1<<j)-1<=n<<1;i++) st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);for(int j=1;j<20;j++) for(int i=1;i<=n;i++) up[i][j]=up[up[i][j-1]][j-1];// cout<<calc(4,3)<<'\n';sg.build(1,n,1);for(int i=1;i<=n;i++){Node t=sg.query(1,n,1,dfn[i],dfn[i]+siz[i]-1);f[i]=calc(t.u,t.v);int l1=1,r1=dfn[i]-1;int l2=dfn[i]+siz[i],r2=n;if(l1<=r1&&l2<=r2) t=sg.pushup(sg.query(1,n,1,l1,r1),sg.query(1,n,1,l2,r2));else if(l1<=r1) t=sg.query(1,n,1,l1,r1);else t=sg.query(1,n,1,l2,r2);g[i]=calc(t.u,t.v);}// for(int i=1;i<=n;i++) cout<<rv[i]<<' ';cout<<'\n';while(q--){int x=read(),y=read(),ans;// cerr<<"+++"<<'\n';if(x==y) ans=f[1];//y是x的祖先else if(dfn[y]<=dfn[x]&&dfn[x]<=dfn[y]+siz[y]-1) ans=g[get_low_anc(y,x)];else ans=f[y];if(ans%3==2) puts("Yohane");else puts("Riko");}return 0;
}D
首先枚举从 0 0 0 开始顺时针和逆时针到的位置,然后选短的一条走两遍,现在问题便成了一段区间中最多能选多少个数,使它们的和不超过 l i m i t limit limit,这可以用优先队列维护
这样 O ( n 2 ) O(n^2) O(n2) 暴力就写完了,打表发现顺时针走到的位置增加时,逆时针走到的最优位置也会增加,这就是决策单调性
考虑用分治的方法解决决策单调性问题,里面用线段树进行维护
时间复杂度 O ( n l o g 2 n ) O(nlog^2n) O(nlog2n)
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=100100;
int n,T,ans,d[N],t[N],d1[N],d2[N];
int cnt,disc[N];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
struct Segment{int seg[N<<2],tot[N<<2];void modify(int l,int r,int x,int pos,int val){if(l==r){ seg[x]+=val*disc[l],tot[x]+=val;return;}int mid=(l+r)>>1;if(mid>=pos) modify(l,mid,x<<1,pos,val);else modify(mid+1,r,x<<1^1,pos,val);seg[x]=seg[x<<1]+seg[x<<1^1],tot[x]=tot[x<<1]+tot[x<<1^1];}int query(int l,int r,int x,int limit){if(l==r) return min(tot[x],limit/disc[l]);int mid=(l+r)>>1;if(limit>seg[x<<1]) return tot[x<<1]+query(mid+1,r,x<<1^1,limit-seg[x<<1]);else return query(l,mid,x<<1,limit);}
}sg;
void solve(int l,int r,int tl,int tr){if(l>r) return;int mid=(l+r)>>1;for(int i=max(1ll,l);i<=mid;i++) sg.modify(1,n,1,t[i],1);int bpos=tr,mx=0;for(int k=tr;k>=max(mid+1,tl);k--){if(k<=n) sg.modify(1,n,1,t[k],1);int D=d1[mid]-d[mid],DD=d2[k];int left=T-min(D,DD)*2-max(D,DD);if(left<0) continue;int res=sg.query(1,n,1,left);// cout<<mid<<' '<<k<<' '<<left<<' '<<res<<'\n';if(mx<=res) mx=res,bpos=k;}for(int k=min(tr,n);k>=max(mid+1,tl);k--) sg.modify(1,n,1,t[k],-1);// cout<<l<<' '<<r<<' '<<tl<<' '<<tr<<' '<<sg.query(1,n,1,1000000000)<<'\n';ans=max(ans,mx);// cout<<mid<<' '<<bpos<<' '<<mx<<'\n';solve(mid+1,r,bpos,tr);for(int i=max(1ll,l);i<=mid;i++) sg.modify(1,n,1,t[i],-1);for(int i=min(tr,n);i>bpos;i--) sg.modify(1,n,1,t[i],1);solve(l,mid-1,tl,bpos);for(int i=min(tr,n);i>bpos;i--) sg.modify(1,n,1,t[i],-1);
}
signed main(){freopen("decalcomania.in","r",stdin);freopen("decalcomania.out","w",stdout);n=read(),T=read();for(int i=1;i<=n;i++) d[i]=read(),disc[i]=t[i]=read();for(int i=1;i<=n;i++) d1[i]=d1[i-1]+d[i];for(int i=n;i>=1;i--) d2[i]=d2[i+1]+d[i];sort(disc+1,disc+n+1);cnt=unique(disc+1,disc+n+1)-disc-1;for(int i=1;i<=n;i++) t[i]=lower_bound(disc+1,disc+cnt+1,t[i])-disc;// for(int i=1;i<=n;i++) cout<<t[i]<<' ';cout<<'\n';solve(0,n,1,n+1);printf("%lld",ans);return 0;
}相关文章:

20230830比赛总结
分数 预估分数: 100 100 [ 0 , 20 ] 100 [ 300 , 320 ] 100100[0,20]100[300,320] 100100[0,20]100[300,320] 实际分数: 100 100 10 100 310 10010010100310 10010010100310 反思 B 只是粗略观察表就急于写决策单调性优化,写完后…...
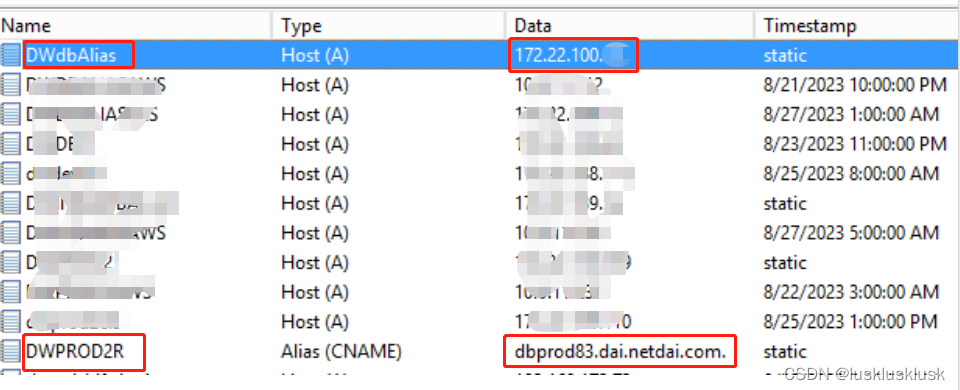
DNS指向别名还是IP
现在有一台服务器dbprod126,ip是172.22.100.4 现在有一个需求,需要在dns中对dbprod126建一个别名wondadb3r的记录,也就是ping wondadb3r的时候显示的是dbprod126的ip,目前有两种方法,主要使用方法1指向别名…...

【考研数学】概率论与数理统计 —— 第二章 | 一维随机变量及其分布(1,基本概念与随机变量常见类型)
文章目录 引言一、一维随机变量及其分布1.1 随机变量1.2 分布函数 二、随机变量常见类型及分布2.1 离散型随机变量2.2 连续型随机变量及概率密度函数 写在最后 引言 暑假接近尾声了,争取赶一点概率论部分的进度。 一、一维随机变量及其分布 1.1 随机变量 设随机试…...
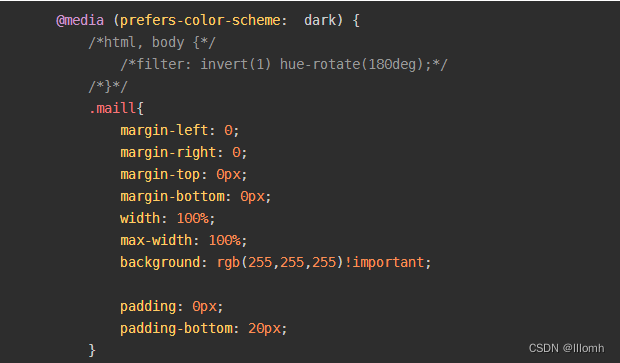
CSS判断手机暗黑模式
手机有个功能到了晚上会自动变成深色也就是暗黑模式.这种情况下网页会自动变颜色.如果想自由控制暗黑模式下的html样式的话,可以用如下方式: media (prefers-color-scheme: dark) {/*html, body {*//*filter: invert(1) hue-rotate(180deg);*//*}*/.maill{margin-left: 0;marg…...
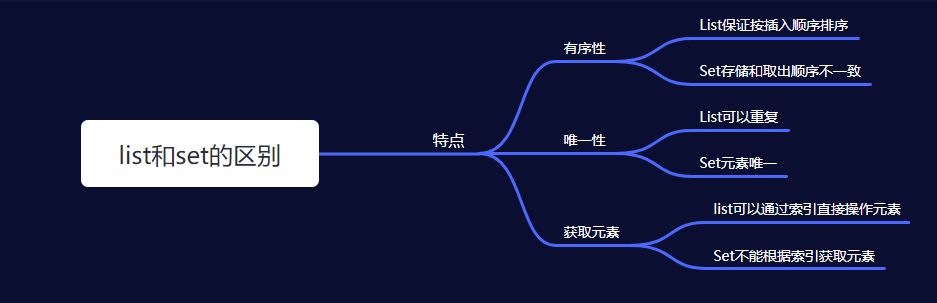
【java中的Set集合】HashSet、LinkedHashSet、TreeSet(最通俗易懂版!!)
目录 一、HashSet集合 1.HashSet集合的特点 2.HashSet常用方法 二、LinkedHashSet集合 LinkedHashSet集合的特点 三、TreeSet集合 1.TreeSet集合的特点 2.TreeSet的基本使用 四、HashSet、LinkedHashSet、TreeSet的使用场景 五、list和set集合的区别 一、HashSet集合 …...

python中的文件操作
我们平常对文件的基本操作,大概可以分为三个步骤(简称文件操作三步走): ① 打开文件 ② 读写文件 ③ 关闭文件 【注意事项】 注意:可以只打开和关闭文件,不进行任何读写 文件打开 open函数ÿ…...

spark支持深度学习批量推理
背景 在数据量较大的业务场景中,spark在数据处理、传统机器学习训练、 深度学习相关业务,能取得较明显的效率提升。 本篇围绕spark大数据背景下的推理,介绍一些优雅的使用方式。 spark适用场景 大数据量自定义方法处理、类sql处理传统机器…...

代码随想录打卡—day52—【子序列问题】— 8.31 最大子序列
共性 做完下面三题,发现三个的dp数组中i都是以 i 为结束的字串。 1 300. 最长递增子序列 300. 最长递增子序列 AC: class Solution { public:int dp[10010]; // 表示以i结束的子序列最大的长度/*if(nums[j] > nums[i])dp[j] max(dp[j],dp[i] …...

gcc4.8.5升级到gcc4.9.2
第1步:获取repo [rootlocalhost SPECS]# wget --no-check-certificate https://copr.fedoraproject.org/coprs/rhscl/devtoolset-3/repo/epel-6/rhscl-devtoolset-3-epel-6.repo -O /etc/yum.repos.d/devtoolset-3.repo --2021-12-07 20:53:26-- https://copr.fedo…...
:常用函数)
Golang 中的 archive/zip 包详解(三):常用函数
Golang 中的 archive/zip 包用于处理 ZIP 格式的压缩文件,提供了一系列用于创建、读取和解压缩 ZIP 格式文件的函数和类型,使用起来非常方便,本文讲解下常用函数。 zip.OpenReader 定义如下: func OpenReader(name string) (*R…...

微服务架构七种模式
微服务架构七种模式 目录概述需求: 设计思路实现思路分析 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy,skip hardness,make a better result,wait for change,challenge Survive.…...
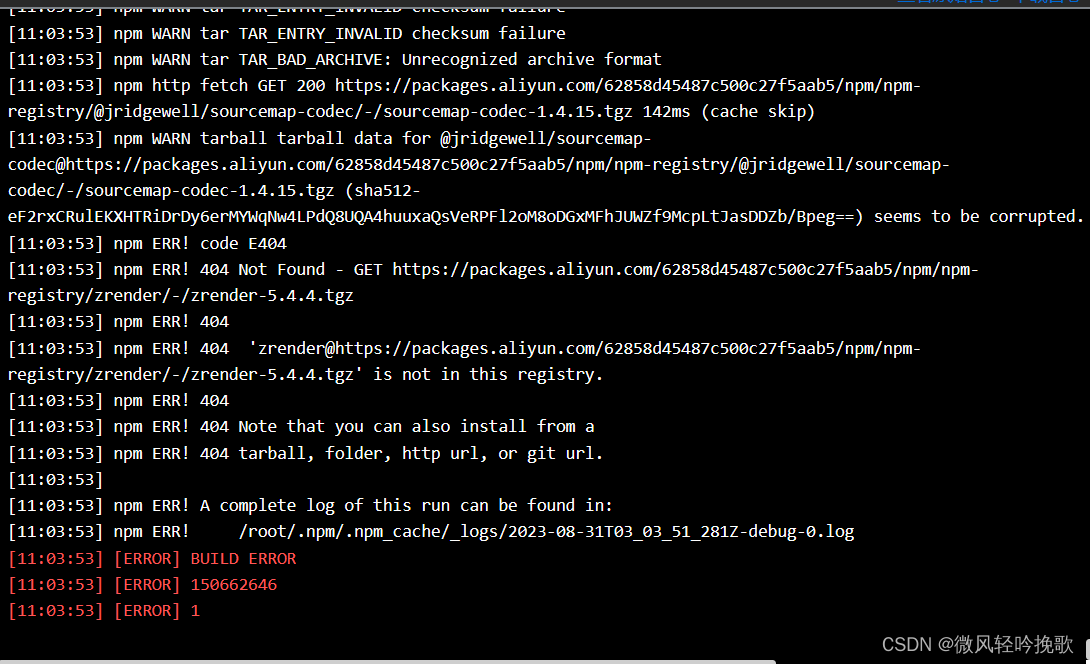
关于CICD流水线的前端项目运行错误,npm项目环境配置时出现报错:Not Found - GET https://registry.npm...
关于CICD流水线的前端项目运行错误,npm项目环境配置时出现报错:Not Found - GET https://registry.npm… 原因应该是某些jar包缓存中没有需要改变镜像将包拉下来 npm config set registry http://registry.npm.taobao.org npm install npm run build...

element-plus的周选择器 一周从周一开始
1、代码 1)、template中 <el-date-picker v-model"value1" type"week" format"[Week] ww" placeholder"巡访周" change"change"value-format"YYYY-MM-DD" /> 2)、方法中 import…...

Android 9.0 pms获取应用列表时过滤掉某些app功能实现
1.前言 在9.0的系统rom定制化开发中,对系统定制的功能也是很多的,在一次产品开发中,要求在第三方app获取应用列表的时候,需要过滤掉某些app,就是不显示在app应用列表中,这就需要在pms查询app列表时过滤掉这些app就可以了,接下来就实现这些功能 2.pms获取应用列表时过滤掉…...

HTML <thead> 标签
实例 带有 thead、tbody 以及 tfoot 元素的 HTML 表格: <table border="1"><thead><tr><th>Month</th><th>Savings</th></tr></thead><tfoot><tr><td>Sum</td><td>$180<…...

谷歌发布Gemini以5倍速击败GPT-4
在Covid疫情爆发之前,谷歌发布了MEENA模型,短时间内成为世界上最好的大型语言模型。谷歌发布的博客和论文非常可爱,因为它特别与OpenAI进行了比较。 相比于现有的最先进生成模型OpenAI GPT-2,MEENA的模型容量增加了1.7倍…...
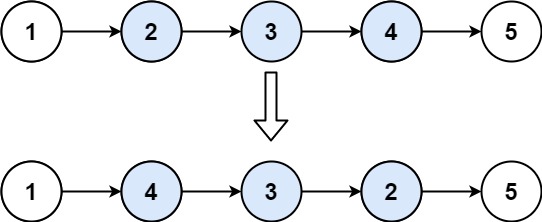
力扣92. 局部反转链表
92. 反转链表 II 给你单链表的头指针 head 和两个整数 left 和 right ,其中 left < right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。 示例 1: 输入:head [1,2,3,4,5], left 2, right 4 输出&am…...

九、适配器模式
一、什么是适配器模式 适配器模式(Adapter)的定义如下:将一个类的接口转换成客户希望的另外一个接口,使得原本由于接口不兼容而不能一起工作的那些类能一起工作。 适配器模式(Adapter)包含以下主要角色&…...
使用spring自带的发布订阅来实现发布订阅
背景 公司的项目以前代码里面有存在使用spring自带发布订阅的代码,因此稍微学习一下如何使用,并了解一下这种实现方式的优缺点。 优点 实现方便,代码方面基本只需要定义消息体和消费者,适用于小型应用程序。不依赖外部中间件&a…...
Walmart电商促销活动即将开始,如何做促销活动?需要注意什么?
近日,沃尔玛官宣Baby Days优惠活动将于9月1日正式开始!卖家可以把握机会,通过设置促销定价,以最优惠的婴儿相关产品价格吸引消费者,包括汽车座椅、婴儿车、尿布袋、家具、床上用品、消耗品、婴儿服装、孕妇装等。注意本…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

轻量级Docker管理工具Docker Switchboard
简介 什么是 Docker Switchboard ? Docker Switchboard 是一个轻量级的 Web 应用程序,用于管理 Docker 容器。它提供了一个干净、用户友好的界面来启动、停止和监控主机上运行的容器,使其成为本地开发、家庭实验室或小型服务器设置的理想选择…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...
