【数据结构】多叉树转换为二叉树-c++代码实现-POJ 3437 Tree Grafting
文章目录
- 写这个题目的原因
- 寻找提交网址
- 题目解决思路
- AC代码
- 成功AC
写这个题目的原因
1、今天在看王道考研数据结构的课(虽然我要保研,但是因为这些看保研面试的时候会问,所以看一下嘞orz),看到了这个多叉树转换为二叉树的知识点。
2、上学期上编译原理课的时候老师上课也提问过这个问题,所以今天尝试着用c++的代码实现一下。
寻找提交网址
1、POJ不知道为什么,提交任何代码都一直报错
(目前时间为2023年8月30日)
然后我去了洛谷、AcWing、LeetCode、PTA都没有搜到这个题目。。。
2、无奈之下去了VJudge,最终在一个韩国的OJ上提交了这个题目,并成功AC,中间的过程也算是一波三折。
这里附上提交的网址:
Tree Grafting(韩国的OJ)
Tree Grafting(POJ)
题目解决思路
题目输入有多行,每行代表一个建树的过程,由d或者u组成。d表示往下新建节点,u表示往上走到当前节点的父亲,这样走下来就得到了一个多叉树。
最终让求解:
1、多叉树的深度,即dep1
2、转换后的二叉树的深度,即dpe2
对于dep1,通过观察输入的字符串可以发现,每一个d即为往下新建一个节点,这里我们可以使用“前缀和”的思想,新建一个变量t,初始值为0,遇到d加一,遇到u减一,在这个过程中最大的t即为要求解的dep1
比如对于题目给出的第一个输入,初始t=0
dudduduudu, 对应的t为
1012121010,所以多叉树的深度为2,即为求解的第一个变量
对于dep2的求解,我们可以对所有的节点设置唯一的一个变量标记(用int就可以实现),然后进行反向建边,用一个一维的数组就可以存储所有的二叉树
当然看到这里有人可能会问,为什么不正向建边?
答:因为这是一个多叉树,一个节点可能有多个儿子,题目的最多节点为10000,那么如果正向建边的话,至少得10000^2大小的数组,可能会爆内存!
这样反向建边之后,我们相当于已经存储了每一个节点的父亲,那么接下来就是很常见的多叉树转换为二叉树的思路了
我们依次遍历所有节点,对于当前节点,如果
1、如果它父亲的左子为空:
那么直接把当前节点作为它父亲的左子
2、如果它父亲的左子不为空:
那么找它父亲左子的最右边的儿子(在这里我们定义为temp),把当前节点作为temp的右子
上面这个点如果不明白,可以百度搜索一下【多叉树怎么转换为二叉树?】会有比较详细的解释
更多细节和注释见代码
AC代码
#include <stdio.h>
#include <cstring>
#include <iostream>
using namespace std;
#define ll long long
#define sf(x) scanf("%d", &x);
#define de(x) cout << x << " ";
#define Pu puts("");
const int N = 2e4 + 9; // 注意这里,题目中说节点最多为1e4,但是字符串长度最多为2e4
int n, m, ans;
int dep1, dep2; // 求解的变量
char s[N]; // 输入的字符串
int fa[N]; // 记录每个节点的父亲
struct E {int dep; // 存储二叉树的数据结构int l, r;
} e[N];
int main() {int now; // 代表当前所处的节点位置int count; // 代表当前新建的节点标号int depTmp; // 统计多叉树的深度int T = 0;while (scanf("%s", s)) {if (s[0] == '#')break;T++;n = strlen(s);for (int i = 0; i < n + 1; i++) {fa[i] = -1; // 所有点标记为没有父亲e[i].l = e[i].r = -1;}now = 0; // 代表当前所处的位置count = 0; // 代表当前新建的节点标号depTmp = dep1 = 0;for (int i = 0; i < n; i++) {if (s[i] == 'd') {count++;fa[count] = now; // 向下,反向建边now = count;depTmp++; // 进行深度统计if (depTmp > dep1)dep1 = depTmp;} else if (s[i] == 'u') {now = fa[now]; // 向上depTmp--;}}e[0].dep = 0;dep2 = 0;for (int i = 1; i <= count; i++) {if (e[fa[i]].l == -1) {e[fa[i]].l = i; // 如果此时父亲节点没有左子,则当前节点作为左子e[i].dep = e[fa[i]].dep + 1;if (e[i].dep > dep2) // 深度更新dep2 = e[i].dep;} else { // 如果已经有了左子int k = e[fa[i]].l;while (e[k].r != -1) {k = e[k].r; // 则找左子的最右孩子}e[k].r = i; // 新的右孩子e[i].dep = e[k].dep + 1;if (e[i].dep > dep2) // 深度更新dep2 = e[i].dep;}}printf("Tree %d: %d => %d\n", T, dep1, dep2);}return 0;
}
成功AC

相关文章:

【数据结构】多叉树转换为二叉树-c++代码实现-POJ 3437 Tree Grafting
文章目录 写这个题目的原因寻找提交网址题目解决思路AC代码成功AC 写这个题目的原因 1、今天在看王道考研数据结构的课(虽然我要保研,但是因为这些看保研面试的时候会问,所以看一下嘞orz),看到了这个多叉树转换为二叉…...
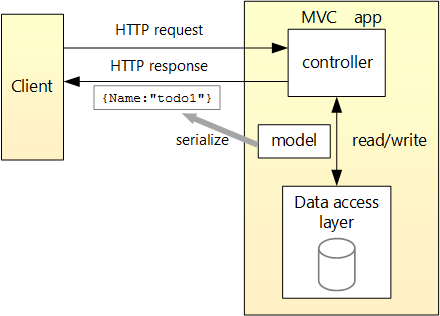
ASP.NET Core 中基于 Controller 的 Web API
基于 Controller 的 Web API ASP.NET Wep API 的请求架构 客户端发送Http请求,Contoller响应请求,并从数据库读取数据,序列化数据,然后通过 Http Response返回序列化的数据。 ControllerBase 类 Web API 的所有controllers 一般…...
iOS系统修复软件 Fix My iPhone for Mac
Fix My iPhone for Mac是一款iOS系统恢复工具。修复您的iPhone卡在Apple徽标,黑屏,冻结屏幕,iTunes更新/还原错误和超过20个iOS 12升级失败。这个macOS桌面应用程序提供快速,即时的解决方案来修复您的iOS系统问题,而不…...

Git企业开发控制理论和实操-从入门到深入(七)|企业级开发模型
前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总 然后就是博主最近最花时间的一个专栏…...

15. 卡牌游戏
目录 题目 思路 C整体代码(含详细注释) 题目 Description 小张在玩一种卡牌游戏,牌组由张牌组成,其中张上写有数字各一张,其余张上全部是数字。 现在牌组经过随机打乱后,小张拿走其中张牌作为手牌&#…...
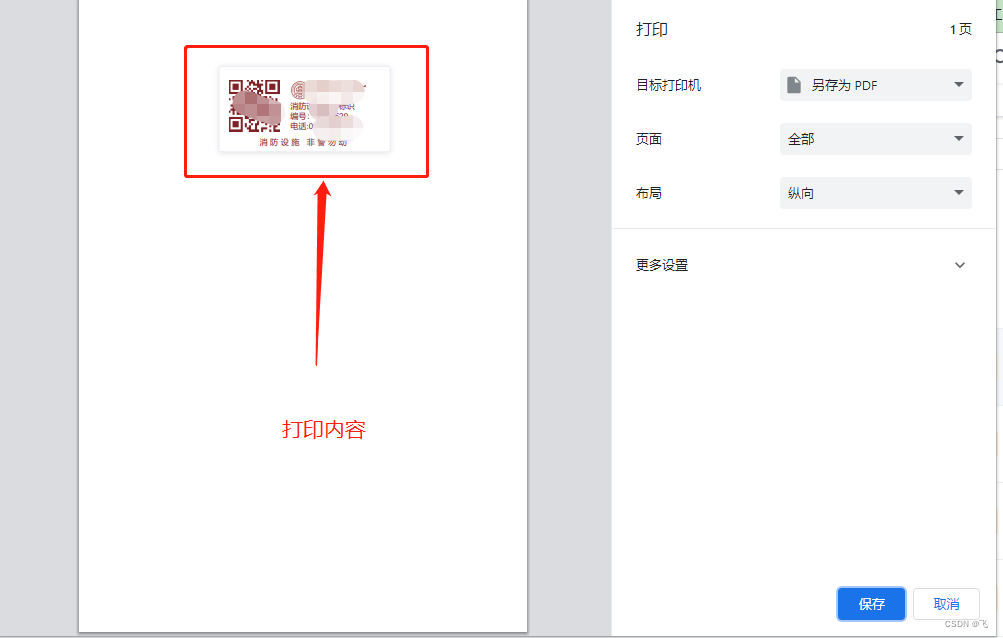
vue使用打印组件print-js
项目场景: 由于甲方要求,项目需要打印二维码标签,故开发此功能 开发流程 安装包:npm install print-js --saveprint-js的使用 <template><div id"print" ref"print" ><p>打印内容<p&…...

20230830比赛总结
分数 预估分数: 100 100 [ 0 , 20 ] 100 [ 300 , 320 ] 100100[0,20]100[300,320] 100100[0,20]100[300,320] 实际分数: 100 100 10 100 310 10010010100310 10010010100310 反思 B 只是粗略观察表就急于写决策单调性优化,写完后…...
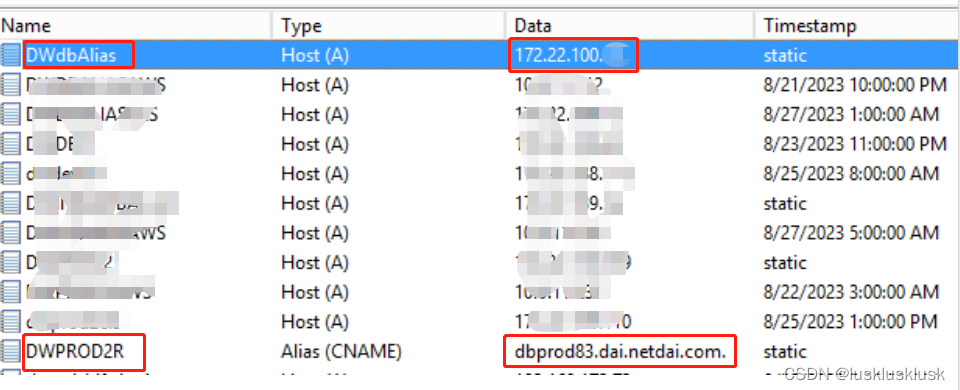
DNS指向别名还是IP
现在有一台服务器dbprod126,ip是172.22.100.4 现在有一个需求,需要在dns中对dbprod126建一个别名wondadb3r的记录,也就是ping wondadb3r的时候显示的是dbprod126的ip,目前有两种方法,主要使用方法1指向别名…...

【考研数学】概率论与数理统计 —— 第二章 | 一维随机变量及其分布(1,基本概念与随机变量常见类型)
文章目录 引言一、一维随机变量及其分布1.1 随机变量1.2 分布函数 二、随机变量常见类型及分布2.1 离散型随机变量2.2 连续型随机变量及概率密度函数 写在最后 引言 暑假接近尾声了,争取赶一点概率论部分的进度。 一、一维随机变量及其分布 1.1 随机变量 设随机试…...
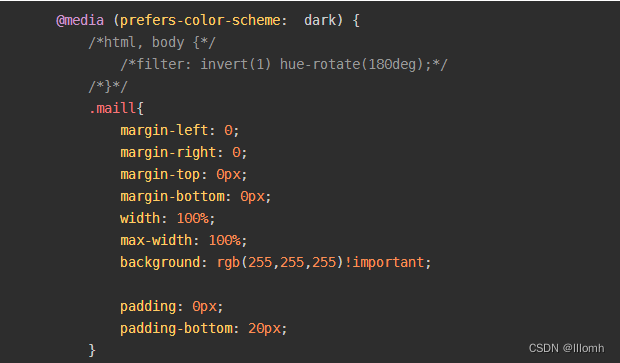
CSS判断手机暗黑模式
手机有个功能到了晚上会自动变成深色也就是暗黑模式.这种情况下网页会自动变颜色.如果想自由控制暗黑模式下的html样式的话,可以用如下方式: media (prefers-color-scheme: dark) {/*html, body {*//*filter: invert(1) hue-rotate(180deg);*//*}*/.maill{margin-left: 0;marg…...
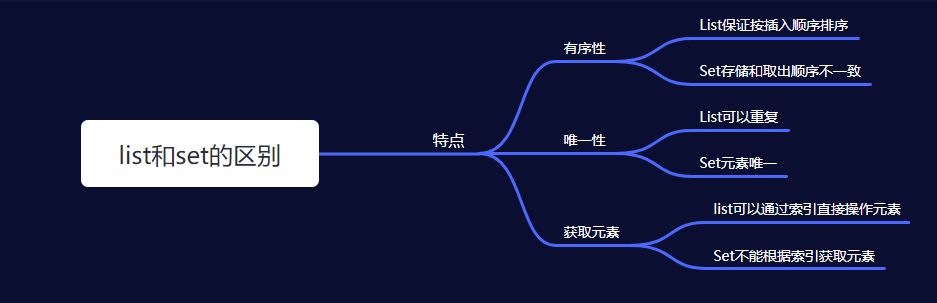
【java中的Set集合】HashSet、LinkedHashSet、TreeSet(最通俗易懂版!!)
目录 一、HashSet集合 1.HashSet集合的特点 2.HashSet常用方法 二、LinkedHashSet集合 LinkedHashSet集合的特点 三、TreeSet集合 1.TreeSet集合的特点 2.TreeSet的基本使用 四、HashSet、LinkedHashSet、TreeSet的使用场景 五、list和set集合的区别 一、HashSet集合 …...

python中的文件操作
我们平常对文件的基本操作,大概可以分为三个步骤(简称文件操作三步走): ① 打开文件 ② 读写文件 ③ 关闭文件 【注意事项】 注意:可以只打开和关闭文件,不进行任何读写 文件打开 open函数ÿ…...

spark支持深度学习批量推理
背景 在数据量较大的业务场景中,spark在数据处理、传统机器学习训练、 深度学习相关业务,能取得较明显的效率提升。 本篇围绕spark大数据背景下的推理,介绍一些优雅的使用方式。 spark适用场景 大数据量自定义方法处理、类sql处理传统机器…...

代码随想录打卡—day52—【子序列问题】— 8.31 最大子序列
共性 做完下面三题,发现三个的dp数组中i都是以 i 为结束的字串。 1 300. 最长递增子序列 300. 最长递增子序列 AC: class Solution { public:int dp[10010]; // 表示以i结束的子序列最大的长度/*if(nums[j] > nums[i])dp[j] max(dp[j],dp[i] …...

gcc4.8.5升级到gcc4.9.2
第1步:获取repo [rootlocalhost SPECS]# wget --no-check-certificate https://copr.fedoraproject.org/coprs/rhscl/devtoolset-3/repo/epel-6/rhscl-devtoolset-3-epel-6.repo -O /etc/yum.repos.d/devtoolset-3.repo --2021-12-07 20:53:26-- https://copr.fedo…...
:常用函数)
Golang 中的 archive/zip 包详解(三):常用函数
Golang 中的 archive/zip 包用于处理 ZIP 格式的压缩文件,提供了一系列用于创建、读取和解压缩 ZIP 格式文件的函数和类型,使用起来非常方便,本文讲解下常用函数。 zip.OpenReader 定义如下: func OpenReader(name string) (*R…...

微服务架构七种模式
微服务架构七种模式 目录概述需求: 设计思路实现思路分析 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy,skip hardness,make a better result,wait for change,challenge Survive.…...
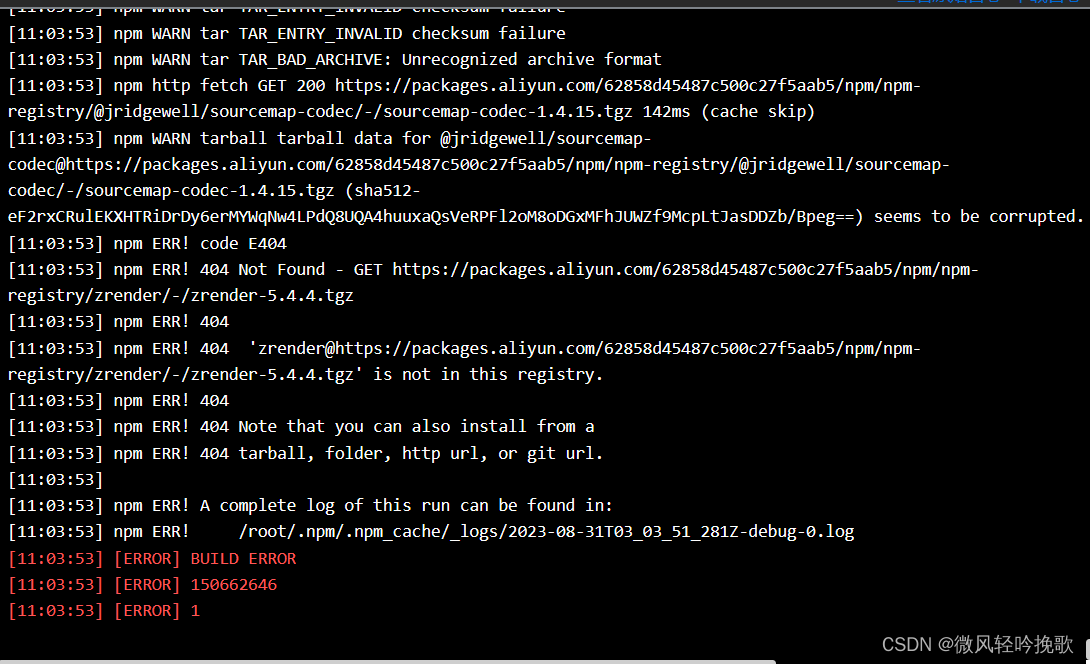
关于CICD流水线的前端项目运行错误,npm项目环境配置时出现报错:Not Found - GET https://registry.npm...
关于CICD流水线的前端项目运行错误,npm项目环境配置时出现报错:Not Found - GET https://registry.npm… 原因应该是某些jar包缓存中没有需要改变镜像将包拉下来 npm config set registry http://registry.npm.taobao.org npm install npm run build...

element-plus的周选择器 一周从周一开始
1、代码 1)、template中 <el-date-picker v-model"value1" type"week" format"[Week] ww" placeholder"巡访周" change"change"value-format"YYYY-MM-DD" /> 2)、方法中 import…...

Android 9.0 pms获取应用列表时过滤掉某些app功能实现
1.前言 在9.0的系统rom定制化开发中,对系统定制的功能也是很多的,在一次产品开发中,要求在第三方app获取应用列表的时候,需要过滤掉某些app,就是不显示在app应用列表中,这就需要在pms查询app列表时过滤掉这些app就可以了,接下来就实现这些功能 2.pms获取应用列表时过滤掉…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
