day 43 | ● 123.买卖股票的最佳时机III ● 188.买卖股票的最佳时机IV
123.买卖股票的最佳时机III


func maxProfit(prices []int) int {dp := make([][]int , len(prices))dp[0] = []int{0, -prices[0], 0, -prices[0], 0}for i := 1; i < len(prices);i++{val0 := dp[i - 1][0]val1 := max(dp[i - 1][0] - prices[i], dp[i - 1][1])val2 := max(dp[i - 1][1] + prices[i], dp[i - 1][2])val3 := max(dp[i - 1][2] - prices[i], dp[i - 1][3])val4 := max(dp[i - 1][3] + prices[i], dp[i - 1][4])dp[i] = []int{val0, val1, val2, val3, val4}}return dp[len(prices)- 1][4]
}
func max(a, b int)int{if a < b{return b}return a
}
● 188.买卖股票的最佳时机IV
和买卖股票3中的思路一样,只不过从两次换成了k次
func maxProfit(k int, prices []int) int {dp := make([][]int, len(prices))for i := 0; i < len(dp); i++{tmp := make([]int, 2 * k + 1)dp[i] = tmpif i == 0{for j := 1; j < 2 * k + 1; j += 2{dp[i][j] = -prices[0]}}}for i := 1; i < len(dp); i++{dp[i][0] = dp[i - 1][0]for j :=1; j < 2 * k + 1; j += 2{dp[i][j] = max(dp[i - 1][j - 1] - prices[i], dp[i - 1][j])dp[i][j + 1] = max(dp[i - 1][j] + prices[i], dp[i - 1][j + 1])}}return dp[len(prices) - 1][2 * k]
}
func max(a , b int)int{if a < b{return b}return a
}
相关文章:

day 43 | ● 123.买卖股票的最佳时机III ● 188.买卖股票的最佳时机IV
123.买卖股票的最佳时机III func maxProfit(prices []int) int {dp : make([][]int , len(prices))dp[0] []int{0, -prices[0], 0, -prices[0], 0}for i : 1; i < len(prices);i{val0 : dp[i - 1][0]val1 : max(dp[i - 1][0] - prices[i], dp[i - 1][1])val2 : max(dp[i - …...
客路旅行(KLOOK)面试(部分)(未完全解析)
一面 用过Chatgpt的哪个版本,了解Chatgpt版本之间的差异吗 什么是优雅部署?newBing: 服务启动时,检查依赖的组件或容器是否就绪,如果不就绪,等待或重试,直到就绪后再注册到服务中心,对外提供服…...

时序预测 | MATLAB实现基于QPSO-BiGRU、PSO-BiGRU、BiGRU时间序列预测
时序预测 | MATLAB实现基于QPSO-BiGRU、PSO-BiGRU、BiGRU时间序列预测 目录 时序预测 | MATLAB实现基于QPSO-BiGRU、PSO-BiGRU、BiGRU时间序列预测效果一览基本描述程序设计参考资料 效果一览 基本描述 1.时序预测 | MATLAB实现基于QPSO-BiGRU、PSO-BiGRU、BiGRU时间序列预测&a…...

el-select码值枚举
当码值的数据是自己写的时候: 例如:isOrNo:[{label:是,value:1},{label:否,value:‘2’}], 当传给后端值时下拉选择是,值为1,我们当前拿到的只是值为value:1࿰…...
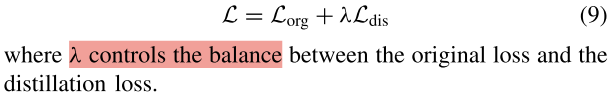
【多面体:知识蒸馏:Pansharpening】
Multipatch Progressive Pansharpening With Knowledge Distillation (基于知识蒸馏的多面体渐进锐化算法) 在这篇文章中,我们提出了一种新的多面体和多级泛锐化方法与知识蒸馏,称为PSDNet。不同于现有的pansharpening方法&…...
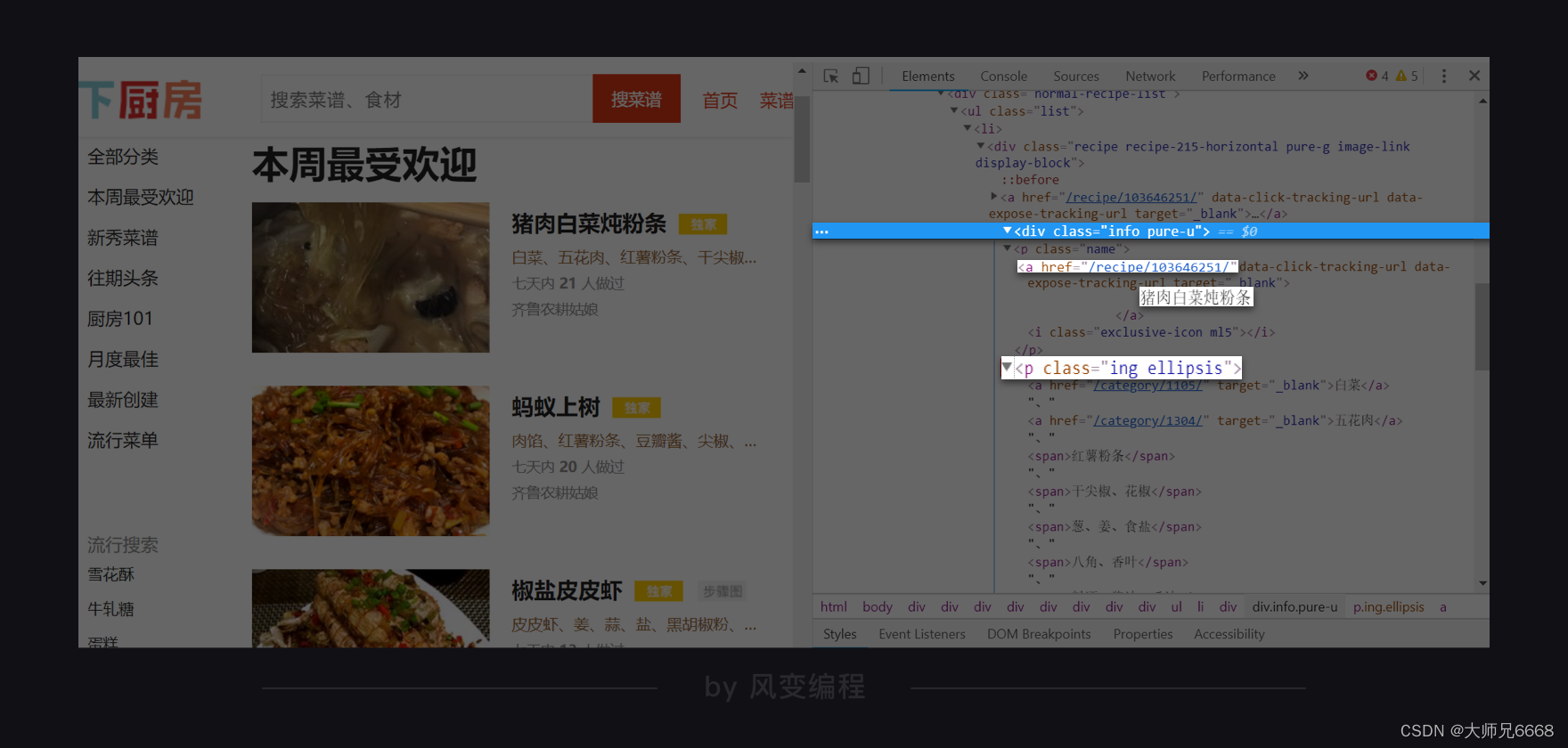
【python爬虫】4.爬虫实操(菜品爬取)
文章目录 前言项目:解密吴氏私厨分析过程代码实现(一)获取与解析提取最小父级标签一组菜名、URL、食材写循环,存列表 代码实现(二)复习总结 前言 上一关,我们学习了用BeautifulSoup库解析数据和…...

深圳发墨西哥专线要多久才能清关?
深圳发往墨西哥专线的货物清关时间会受到多种因素的影响,包括货物的性质、数量、海关政策、运输方式以及货物的文件准备等。下面将详细介绍这些因素对清关时间的影响。 1.货物的性质和数量是影响清关时间的重要因素之一。 一般来说,墨西哥专线中普通商品…...
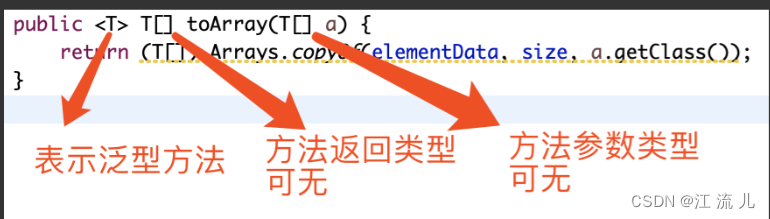
Java-泛型
文章目录 Java泛型什么是泛型?在哪里使用泛型?设计出泛型的好处是什么?动手设计一个泛型泛型的限定符泛型擦除泛型的通配符 结论 Java泛型 什么是泛型? Java泛型是一种编程技术,它允许在编译期间指定使用的数据类型。…...
【python爬虫】8.温故而知新
文章目录 前言回顾前路代码实现体验代码功能拆解获取数据解析提取数据存储数据 程序实现与总结 前言 Hello又见面了!上一关我们学习了爬虫数据的存储,并成功将QQ音乐周杰伦歌曲信息的数据存储进了csv文件和excel文件。 学到这里,说明你已经…...

vue3组合式api 父子组件数据同步v-model语法糖的用法
V-model 大多数情况是用在 表单数据上的, 但它不止这一个作用 父子组件的数据同步, 有一个 语法糖 v-model,这个方法简化了语法, 在elementplus中,都有很多地方使用, 所以我们要理解清楚 父组件 使用 v-mod…...
环境异常总结
1.vue项目 npm run dev 运行时报错:webpack-dev-server --inline --progress --config build/webpack.dev.conf.js 不是内部或外部命令 原因:webpack-dev-server存在问题 解决方案:指定 webpack-dev-server 低版本号 方法: 删除 …...
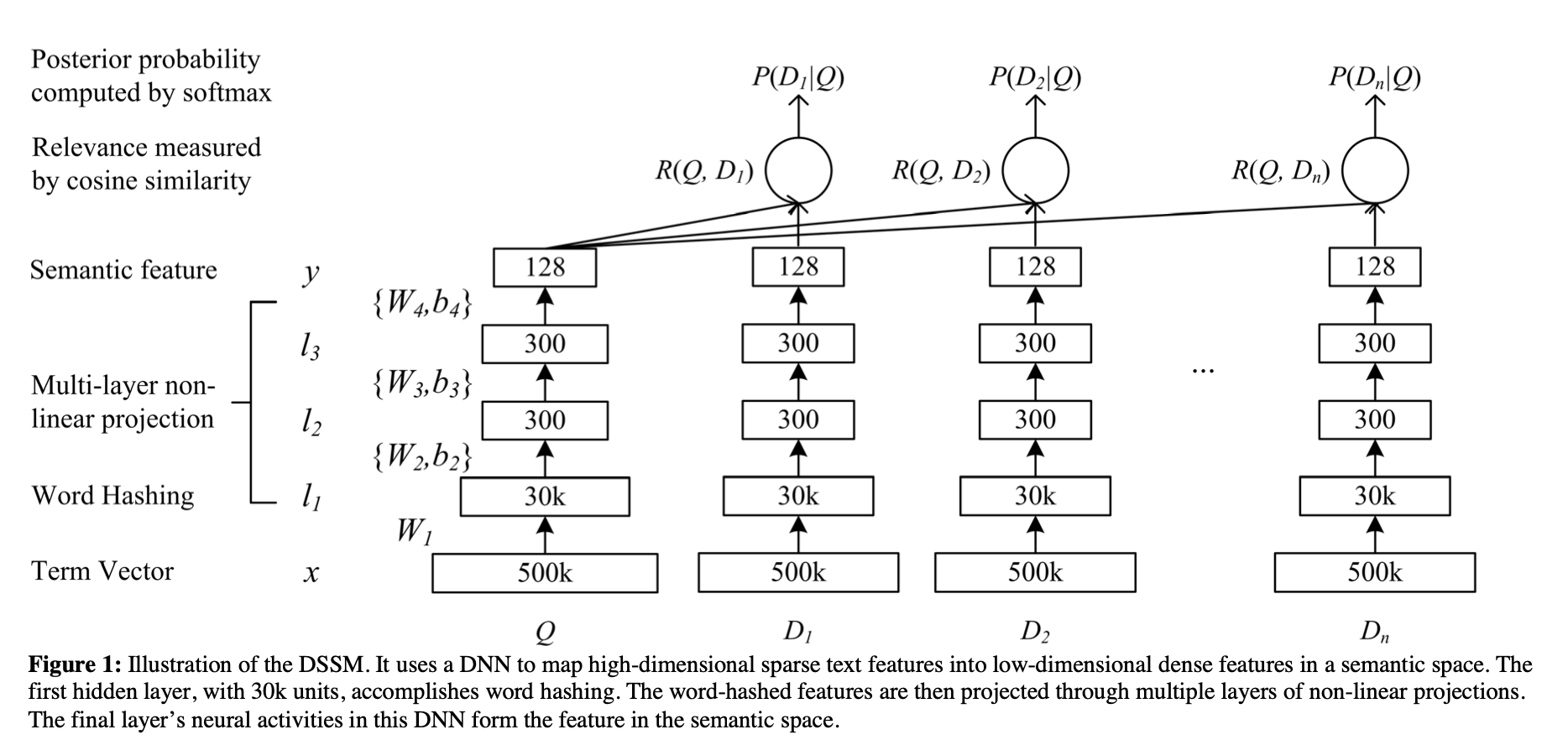
[论文笔记]DSSM
引言 这是DSSM论文的阅读笔记,后续会有一篇文章来复现它并在中文数据集上验证效果。 本文的标题翻译过来就是利用点击数据学习网页搜索中深层结构化语义模型,这篇论文被归类为信息检索,但也可以用来做文本匹配。 这是一篇经典的工作,在DSSM之前,通常使用传统机器学习的…...

Skip Connection——提高深度神经网络性能的利器
可以参考一下这篇知乎所讲 https://zhuanlan.zhihu.com/p/457590578 长跳跃连接用于将信息从编码器传播到解码器,以恢复在下采样期间丢失的信息...
EXCEL中点击单元格,所在行和列都改变颜色
在日常工作中,尤其是办公室工作人群,尝尝需要处理大量的数据,在对数据进行修改时,时长发生看错行的事情,导致数据越改越乱,因此,我常用的一种方法就是选中单元格时,所在行、列标记为…...
)
HAProxy(一)
四层负载均衡与七层负载均衡区别 四层负载均衡和七层负载均衡是两种不同的负载均衡方式,主要区别在于负载均衡的层级及其所支持的协议不同。 四层负载均衡,也称为传输层负载均衡,工作在 OSI 模型的传输层(第四层)&am…...
LeetCode--HOT100题(46)
目录 题目描述:114. 二叉树展开为链表(中等)题目接口解题思路代码 PS: 题目描述:114. 二叉树展开为链表(中等) 给你二叉树的根结点 root ,请你将它展开为一个单链表: 展开后的单链…...

深度探索JavaScript中的原型链机制
🏆作者简介,黑夜开发者,全栈领域新星创作者✌,CSDN博客专家,阿里云社区专家博主,2023年6月csdn上海赛道top4。 🏆数年电商行业从业经验,历任核心研发工程师,项目技术负责…...
一种基于WinDump自动抓包实现方法
本发明的技术方案包括以下步骤和组件: 配置抓包参数:设置抓包的IP、端口以及过滤包大小等参数,以控制抓取的数据范围。循环自动抓包:利用WinDump工具实现循环自动抓包功能,类似于记录日志的方式保留抓包数据。当抓包数…...

taro 支付宝/微信小程序/h5 上传 - base64的那些事儿
支付宝小程序临时path转base64 - 基础库2.0以下 function getImageInfo(path) {return new Promise(resolve > {my.getImageInfo({src: path,success: res > {resolve(res)}})}) } export async function getBase64InAlipay({ id, path }) {const { width, height } awa…...

java之SpringBoot基础、前后端项目、MyBatisPlus、MySQL、vue、elementUi
文章目录 前言JC-1.快速上手SpringBootJC-1-1.SpringBoot入门程序制作(一)JC-1-2.SpringBoot入门程序制作(二)JC-1-3.SpringBoot入门程序制作(三)JC-1-4.SpringBoot入门程序制作(四)…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
