R语言随机波动模型SV:马尔可夫蒙特卡罗法MCMC、正则化广义矩估计和准最大似然估计上证指数收益时间序列...
全文链接:http://tecdat.cn/?p=31162
最近我们被客户要求撰写关于SV模型的研究报告,包括一些图形和统计输出(点击文末“阅读原文”获取完整代码数据)。
相关视频
本文做SV模型,选取马尔可夫蒙特卡罗法(MCMC)、正则化广义矩估计法和准最大似然估计法估计。
模拟SV模型的估计方法:
sim <- svsim(1000,mu=-9, phi = 0.97, sigma = 0.15)print(sim)summary(sim)
plot(sim)
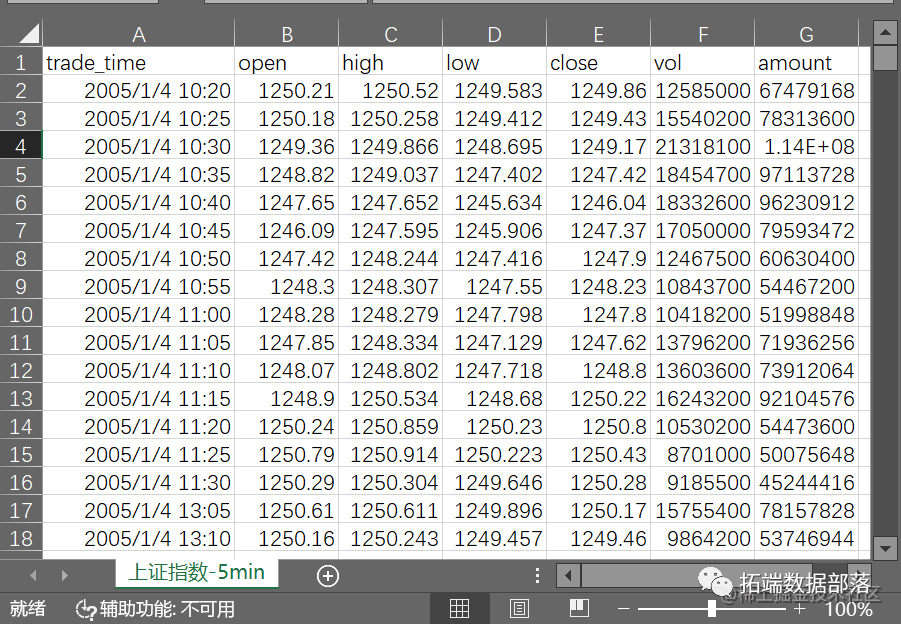
绘制上证指数收益时间序列图、散点图、自相关图与偏自相关图
我们选取上证指数5分钟高频数据:
data=read.csv("上证指数-5min.csv",header=TRUE)
#open:开盘价 close:收盘价 vol:成交量 amount:成交额
head(data,5) #观察数据的头5行
tail(data,5) #观察数据的最后5行
Close.ptd<-data$close
Close.rtd<-diff(log(Close.ptd)) #指标一:logReturn
rets=diff(data$close)/data$close[-length(data$close)] #指标二:Daily Returns,我们选择Daily Returns
library(tseries)
adf.test(rets)## 绘制上证指数收益时间序列图、散点图、自相关图与偏自相关图
Close.ptd.ts<-ts(Close.ptd,start=c(2005,1,4),freq=242)
plot(Close.ptd.ts, type="l",main="(a) 上证指数日收盘价序列图",acf(Close.rtd,main='',xlab='Lag',ylab='ACF',las=1)
title(main='(b) 上证指数收益率自相关检验',cex.main=0.95)pacf(Close.rtd,main='',xlab='Lag',ylab='PACF',las=1)
title(main='(c) 上证指数收益率偏自相关检验',cex.main=0.95)
def.off## Q-Q图、经验累积分布ecdf图、密度图、直方图
qqnorm(Close.rtd,main="(a) 上证指数收益率Q-Q图",cex.main=0.95,xlab='理论分位数',ylab='样本分位数')
qqline(Close.rtd)
#经验累积分布ecdf图
plot(ECD,lwd = 2,main="(b) 上证指数收益率累积分布函数图",cex.main=0.95,las=1)
xx <- unique(sort(c(seq(-3, 2, length=24), knots(ECD))))
abline(v = knots(ECD), lty=2, col='gray70')
x1 <- c((-4):3) # 设定区间范围
lines(x1,pnorm(x1,mean(Close.rtdC[1:10]),sd(Close.rtd[1:10])))
#密度图
plot(D, main="(c) 上证指数核密度曲线图 ",xlab="收益", ylab='密度',xlim = c(-7,7), ylim=c(0,0.5),cex.main=0.95)
polygon(D, col="gray", border="black")
curve(dnorm,lty = 2, add = TRUE) lines(x2,dnorm(x2,mean=0,sd=1))
abline(v=0,lty = 3)
legend("topright", legend=c("核密度","正态密度"),lty=c(1,2),cex=0.5)
#直方图
hist(Close.rtd[1:100],xaxt='n',main='(d) 上证指数收益率直方图',xlab='收益/100',ylab='密度', freq=F,cex.main=0.95,las=1)
lines(x2,dnorm(x2,mean(Close.rtd[1:100]),sd(Close.rtd[1:100])))
axis(1,at=axTicks(1),labels = as.integer(axTicks(1))/100 )
点击标题查阅往期内容

【视频】随机波动率SV模型原理和Python对标普SP500股票指数预测|数据分享

左右滑动查看更多

01
02
03

04
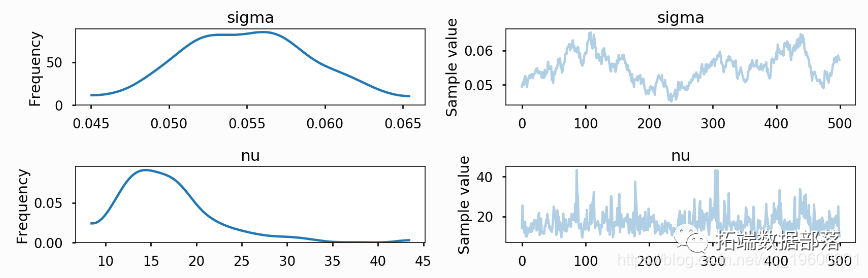
SV模型
{N <- length(logReturn)mu <- (1/N)*sum(logReturn)sqrt((1/N) * sum((logReturn - mu)^2))
}return=-1.5*log(h)-y^2/(2*h)-(log(h)-mu)^2/(2*sigma2)
}马尔可夫链蒙特卡罗估计
该模型使用了Kastner和Fruhwirth-Schnatter所描述的算法。使用的R代码是:
###Markov Chain Monte Carlosummary(mcmc)
准最大似然估计
SV模型可以用QML方法在R中用许多不同的状态空间和Kalman滤波包来估计。
a0=c(parm[1])P0=matrix(parm[3]^2/(1-parm[2]^2))dt=matrix(parm[1]*(1-parm[2]))ct=matrix(-1.27)Tt=matrix(parm[2])Zt=matrix(1)HHt=matrix(parm[3]^2)GGt=matrix(pi^2/2)ans<-fkf(a0=sp$a0,P0=sp$P0,dt=sp$dt,ct=sp$ct,Tt=sp$Tt,Zt=sp$Zt,HHt=sp$HHt,GG
正则化广义矩阵
在R函数中定义矩条件,然后估计参数0。
moments <- c (m1 = sqrt(2/pi)*exp(mu/2 + sig2h/8),m2 = exp(mu + sig2h/2 ) ,m3 = 2*sqrt ( 2/pi ) * exp( 3*mu/2 + 9*sig2h/8 ) ,gmm(g = sv.moments , x =rets , t0=c(mu=-10, phi=0.9,sigmaeta= 0.2),

点击文末“阅读原文”
获取全文完整代码数据资料。
本文选自《R语言随机波动模型SV:马尔可夫蒙特卡罗法MCMC、正则化广义矩估计和准最大似然估计上证指数收益时间序列》。
点击标题查阅往期内容
HAR-RV-J与递归神经网络(RNN)混合模型预测和交易大型股票指数的高频波动率
Matlab马尔可夫链蒙特卡罗法(MCMC)估计随机波动率(SV,Stochastic Volatility) 模型
R语言隐马尔可夫模型HMM连续序列重要性重抽样CSIR估计随机波动率模型SV分析股票收益率时间序列
马尔可夫Markov区制转移模型分析基金利率
马尔可夫区制转移模型Markov regime switching
时变马尔可夫区制转换MRS自回归模型分析经济时间序列
马尔可夫转换模型研究交通伤亡人数事故时间序列预测
如何实现马尔可夫链蒙特卡罗MCMC模型、Metropolis算法?
Matlab用BUGS马尔可夫区制转换Markov switching随机波动率模型、序列蒙特卡罗SMC、M H采样分析时间序列
R语言BUGS序列蒙特卡罗SMC、马尔可夫转换随机波动率SV模型、粒子滤波、Metropolis Hasting采样时间序列分析
matlab用马尔可夫链蒙特卡罗 (MCMC) 的Logistic逻辑回归模型分析汽车实验数据
stata马尔可夫Markov区制转移模型分析基金利率
PYTHON用时变马尔可夫区制转换(MRS)自回归模型分析经济时间序列
R语言使用马尔可夫链对营销中的渠道归因建模
matlab实现MCMC的马尔可夫转换ARMA - GARCH模型估计
R语言隐马尔可夫模型HMM识别不断变化的股票市场条件
R语言中的隐马尔可夫HMM模型实例
用机器学习识别不断变化的股市状况—隐马尔科夫模型(HMM)
Matlab马尔可夫链蒙特卡罗法(MCMC)估计随机波动率(SV,Stochastic Volatility) 模型
MATLAB中的马尔可夫区制转移(Markov regime switching)模型
Matlab马尔可夫区制转换动态回归模型估计GDP增长率
R语言马尔可夫区制转移模型Markov regime switching
stata马尔可夫Markov区制转移模型分析基金利率
R语言如何做马尔可夫转换模型markov switching model
R语言隐马尔可夫模型HMM识别股市变化分析报告
R语言中实现马尔可夫链蒙特卡罗MCMC模型

![]()

相关文章:

R语言随机波动模型SV:马尔可夫蒙特卡罗法MCMC、正则化广义矩估计和准最大似然估计上证指数收益时间序列...
全文链接:http://tecdat.cn/?p31162 最近我们被客户要求撰写关于SV模型的研究报告,包括一些图形和统计输出(点击文末“阅读原文”获取完整代码数据)。 相关视频 本文做SV模型,选取马尔可夫蒙特卡罗法(MCMC)、正则化广…...
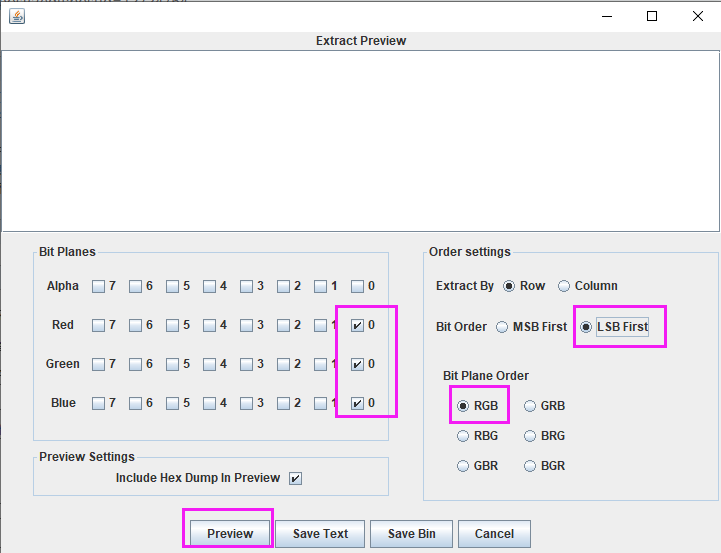
详细教程:Stegsolve的下载,jdk的下载、安装以及环境的配置
最近在学习隐写术,下载stegsolve 以及使用stegsolve倒腾了很久,避免朋友们和我一样倒腾了很久,希望此文可以帮到刚在学习隐写的朋友们(win7下使用stegsolve) 文章目录 一、下载stegsolve链接二、jdk的下载三、jdk的安装四、配置环境变量五、检…...
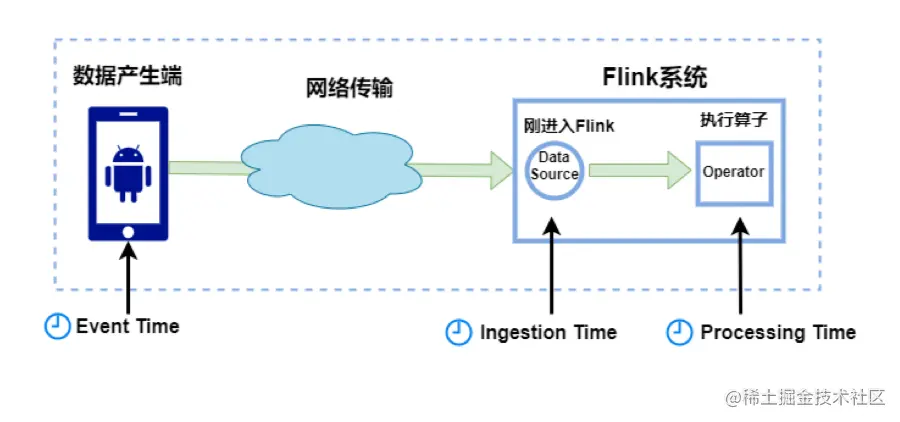
Watermark 是怎么生成和传递的?
分析&回答 Watermark 介绍 Watermark 本质是时间戳,与业务数据一样无差别地传递下去,目的是衡量事件时间的进度(通知 Flink 触发事件时间相关的操作,例如窗口)。 Watermark 是一个时间戳, 它表示小于该时间戳的…...

深度学习论文分享(八)Learning Event-Driven Video Deblurring and Interpolation
深度学习论文分享(八)Learning Event-Driven Video Deblurring and Interpolation 前言Abstract1 Introduction2 Motivation2.1 Physical Model of Event-based Video Reconstruction2.2 Spatially Variant Triggering Threshold 3 Proposed Methods3.1 …...

UI设计开发原则
一、一致性原则 坚持以用户体验为中心设计原则,界面直观、简洁,操作方便快捷,用户接触软件后对界面上对应的功能一目了然、不需要太多培训就可以方便使用本应用系统。 1、字体 保持字体及颜色一致,避免一套主题出现多个字体&am…...

Mac 如何判断下载Mac with Intel Chip 还是 Mac with Apple Chip
如下图,当我们在 Mac系统 下载客户端时,有两种选择:Mac with Intel Chip 、 Mac with Apple Chip 如何判断要下载哪一种? 需要判断本机Mac是在Inter芯片还是Apple芯片上运行的。方法如下: 点击屏幕左上角Apple标志&a…...

windows笔记本远程连接如何打开任务管理器?
参考素材: https://jingyan.baidu.com/article/8275fc86a97f5207a03cf6cd.html https://www.anyviewer.cn/how-to/ctrl-alt-delete-remote-desktop-6540.html 网上查了很多方法,都说ctrlaltend可以解决这个问题。 但是笔记本键盘上没有end键。 继续查了一…...
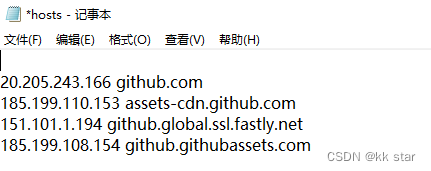
GitHub打不开解决方法——授人以渔
打不开GitHub的原因之一,DNS地址解析到了无法访问的ip。(为什么无法访问?) 1、打开GitHub看是哪个域名无法访问,F12一下 2、DNS解析看对应的域名目前哪个IP可以访问 DNS解析的网址: (1&#x…...

gRPC之数据压缩Snappy、zstd
文章目录 gRPC之数据压缩Snappy一、背景二、什么是snappy1. Snappy适合场景 三、demo: Go代码实现了一个snappy压缩格式的压缩器for grpc1. 这段代码怎么保证并发安全的? 四、什么是zstd五、 zstd和snappy有什么区别,如何选择?六、demo: Go代码实现了一个zstd压缩格…...

k8s之存储篇---存储类StorageClass
介绍 StorageClass 为管理员提供了描述存储"类"的方法。 不同的类型可能会映射到不同的服务质量等级或备份策略,或是由集群管理员制定的任意策略。 Kubernetes 本身并不清楚各种类代表的什么。这个类的概念在其他存储系统中有时被称为"配置文件&quo…...
WordPress(4)关于网站的背景图片更换
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、更改的位置1. 红色区域是要更换的随机的图片二、替换图片位置三.开启随机数量四.结束前言 提示:这里可以添加本文要记录的大概内容: 例如:随着人工智能的不断发展,机器学习这门技术也…...
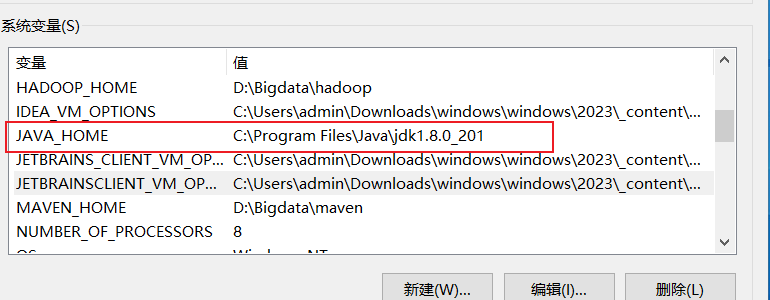
2 | Window 搭建单机 Hadoop 和Spark
搭建单机 Hadoop 和 Spark 环境可以学习和测试大数据处理的基础知识。在 Windows 操作系统上搭建这两个工具需要一些配置和设置,下面是一个详细的教程: 注意: 在开始之前,请确保你已经安装了 Java 开发工具包(JDK),并且已经下载了 Hadoop 和 Spark 的最新版本。你可以从…...

接口测试与功能测试的区别~
今天为大家分享的是我们在日常测试工作中, 一定会接触并且目前在企业中是主要测试内容的 功能测试与接口测试 一.功能测试与接口测试的基本概念。 1.1 什么是功能测试呢? 功能测试: 是黑盒测试的一方面, 检查实际软件的功能是否符合用户的需求 功能测试测试的内容包括以下…...
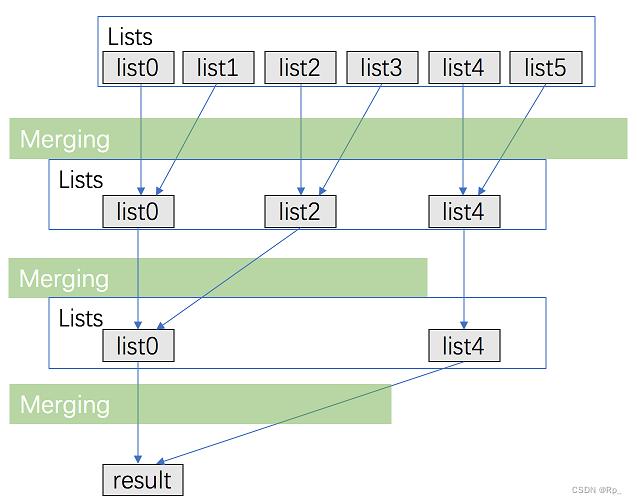
LeetCode 23 合并 K 个升序链表
LeetCode 23 合并 K 个升序链表 来源:力扣(LeetCode) 链接:https://leetcode.cn/problems/merge-k-sorted-lists/description/ 博主Github:https://github.com/GDUT-Rp/LeetCode 题目: 给你一个链表数组…...

[国产MCU]-W801开发实例-TCP客户端
TCP客户端 文章目录 TCP客户端1、TCP协议简单介绍2、W801创建TCP客户流程本文将详细介绍如何在W801中使用TCP客户端。 1、TCP协议简单介绍 传输控制协议 (TCP) 是一种标准,它定义了如何建立和维护应用程序可以用来交换数据的网络对话。 TCP 与 Internet 协议 (IP) 一起工作,…...
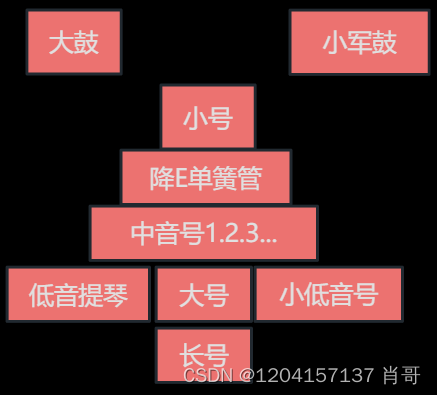
《爵士乐史》乔德.泰亚 笔记
第一章 【美国音乐的非洲化】 【乡村布鲁斯和经典布鲁斯】 布鲁斯:不止包括忧愁、哀痛 十二小节布鲁斯特征: 1.乐型(A:主、B:属、C/D:下属):A→A→B→A→C→D→A→A 2.旋律:大三、小三、降七、降五 盲人…...

工程制造领域:企业IT架构
一、IT组织规划架构图 1.1 IT服务保证梯队与指导思想 二、整体业务规划架构图 三、数据化项目规划架构图 四、应用系统集成架构图...

PY32F003F18点灯
延时函数学习完之后,可以学习PY32F003F18的GPIO输出功能。 1、Debug引脚默认被置于复用功能上拉或下拉模式:PA14默认为SWCLK: 置于下拉模式PA13默认为SWDIO: 置于上拉模式PF4默认为Boot:Boot引脚默认置于输入下拉模式 2、GPIO输出状态&#…...
Mac不想用iTerm2了怎么办
这东西真是让人又爱又恨,爱的是它的UI还真不错,恨的是它把我的环境给破坏啦!让我每次启动终端之后都要重新source激活我的python环境,而且虚拟环境前面没有括号啦!这怎么能忍!在UI和实用性面前我断然选择实…...

x86_64 ansible 源码编译安装
源码 GitHub - ansible/ansible: Ansible is a radically simple IT automation platform that makes your applications and systems easier to deploy and maintain. Automate everything from code deployment to network configuration to cloud management, in a languag…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...
