港陆证券:五日线破位怎么看?
在股票交易中,五日线是个重要的技术指标之一,它能够反映出最近的商场趋势。假如五日线破位,这意味着商场呈现了趋势反转,出资者需求注重趋势改动,并采取相应的出资战略。
首先,咱们来看看五日线破位的原因。一般来说,五日线破位阐明商场心情发生了反转,出资者的心情也会随之发生改动,他们或许会改动自己的出资战略。假如五日线向下破位,这意味着商场处于跌落趋势中,出资者需求警惕风险,能够挑选恰当减仓或是等候上升;假如五日线向上破位,这意味着商场处于上升趋势中,出资者能够挑选增加仓位,把握商场机会。
其次,咱们需求检查五日线破位之后,商场的走势怎么。假如五日线时间短破位,可是很快从头回到五日线之上,那么这仅仅时间短的调整,并不影响商场整体趋势;可是假如五日线一向处于下方,则阐明商场处于跌落趋势中,出资者需求警惕风险。假如五日线向上突破,短期内或许会有一波反弹,可是长期趋势是否能够继续上涨需求仔细调查。
其次,咱们还需求考虑五日线破位的影响因素。有时分五日线破位或许仅仅一时心思反响,而不是实践的商场趋势反转。比方,有些状况下五日线破位仅仅因为出资者的惊惧心情所造成的,这时分需求耐心调查商场的反响以及是否会呈现反弹。
最终,咱们需求说一下出资者应该怎么应对五日线破位的状况。首先,出资者需求坚持冷静,不要被商场心情所左右。其次,需求剖析商场趋势以及重要技术指标的改动,制定恰当的出资战略。最终,坚持慎重,不要盲目跟风,在商场趋势不明朗的时分,能够挑选坚持现金或许挑选低风险的出资品种。
综上所述,五日线破位需求出资者注重,需求从多个视点进行剖析。出资者需求根据商场的实践状况制定相应的出资战略,并且坚持慎重,不要盲目跟风,这样才能够在股票出资中取得更好的收益。
相关文章:

港陆证券:五日线破位怎么看?
在股票交易中,五日线是个重要的技术指标之一,它能够反映出最近的商场趋势。假如五日线破位,这意味着商场呈现了趋势反转,出资者需求注重趋势改动,并采取相应的出资战略。 首先,咱们来看看五日线破位的原因…...

睿趣科技:抖音小店多久可以做起来
随着社交媒体的迅猛发展,抖音成为了全球最受欢迎的短视频平台之一,吸引了数以亿计的用户。在抖音上,人们不仅可以分享自己的生活、才艺和创意,还可以创业经营抖音小店。但是,很多人都想知道,一个抖音小店到…...

onnx 模型切割掉conv后面的节点,设置输出层名称和最后节点名称一致,设置输出层shape和输出节点一致.
某些模型最后卷积层之后的算子不适合在推理引擎里面跑,切割掉conv后面的算子,在cpu上实现有比较好的性能. 包含: 1.获取onnx中间节点的shape的示例 2.增加onnx模型输出,设…...
泛型的学习
泛型深入 泛型:可以在编译阶段约束操作的数据类型,并进行检查 泛型的格式:<数据类型> 注意:泛型只能支持引用数据类型 //没有泛型的时候,集合如何存储数据//如果我们没有给集合指定类型,默认认为…...
 测试点全过)
L1-061 新胖子公式(Python实现) 测试点全过
前言: {\color{Blue}前言:} 前言: 本系列题使用的是,“PTA中的团体程序设计天梯赛——练习集”的题库,难度有L1、L2、L3三个等级,分别对应团体程序设计天梯赛的三个难度。更新取决于题目的难度,…...
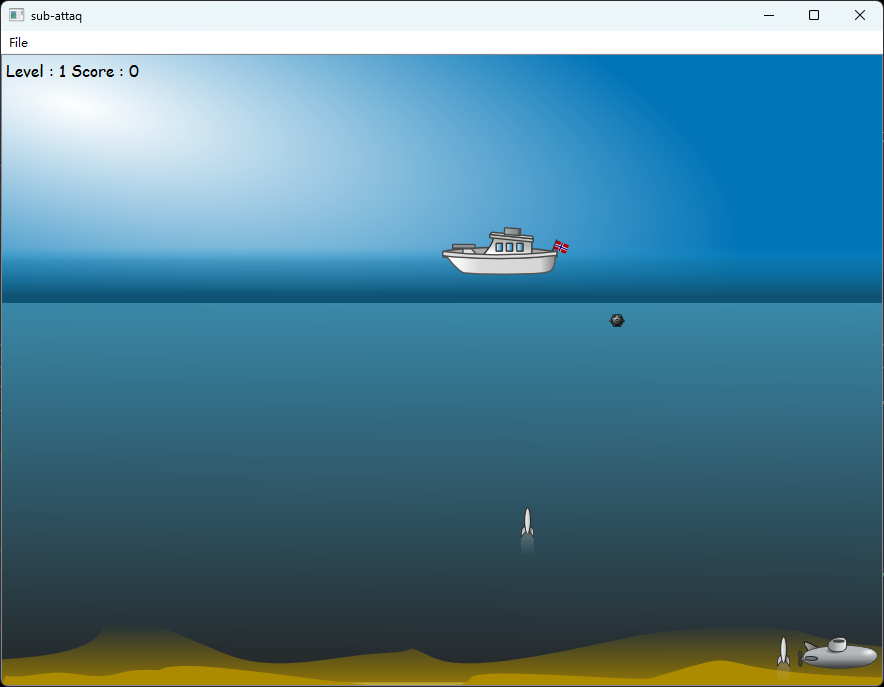
潜艇来袭(Qt官方案例-2维动画游戏)
一、游戏介绍 1 开始界面 启动程序,进入开始界面。 2 开始新游戏 点击菜单:File》New Game (或者CtrlN)进入新游戏。 开始新游戏之后,会有一个海底的潜艇,和水面舰艇对战。 计算机:自动控制…...

50ETF期权开户平台(0门槛期权开户指南)
50ETF期权开户平台比较好的有:期权馆,期权科普馆,小熊期权,期权酱,财顺财经,财顺期权等,都是国内前十的期权分仓平台,下文为大家结算50ETF期权开户平台(0门槛期权开户指南…...

leaflet · 关于轨迹移动
1.引入 import MovingMarker from "../src/utils/MovingMarker"; 2.MovingMarker.js内容 import L from "leaflet"; import eventBus from ../util/eventBus; L.interpolatePosition function(p1, p2, duration, t) {var k t/duration;k (k > 0) ? …...
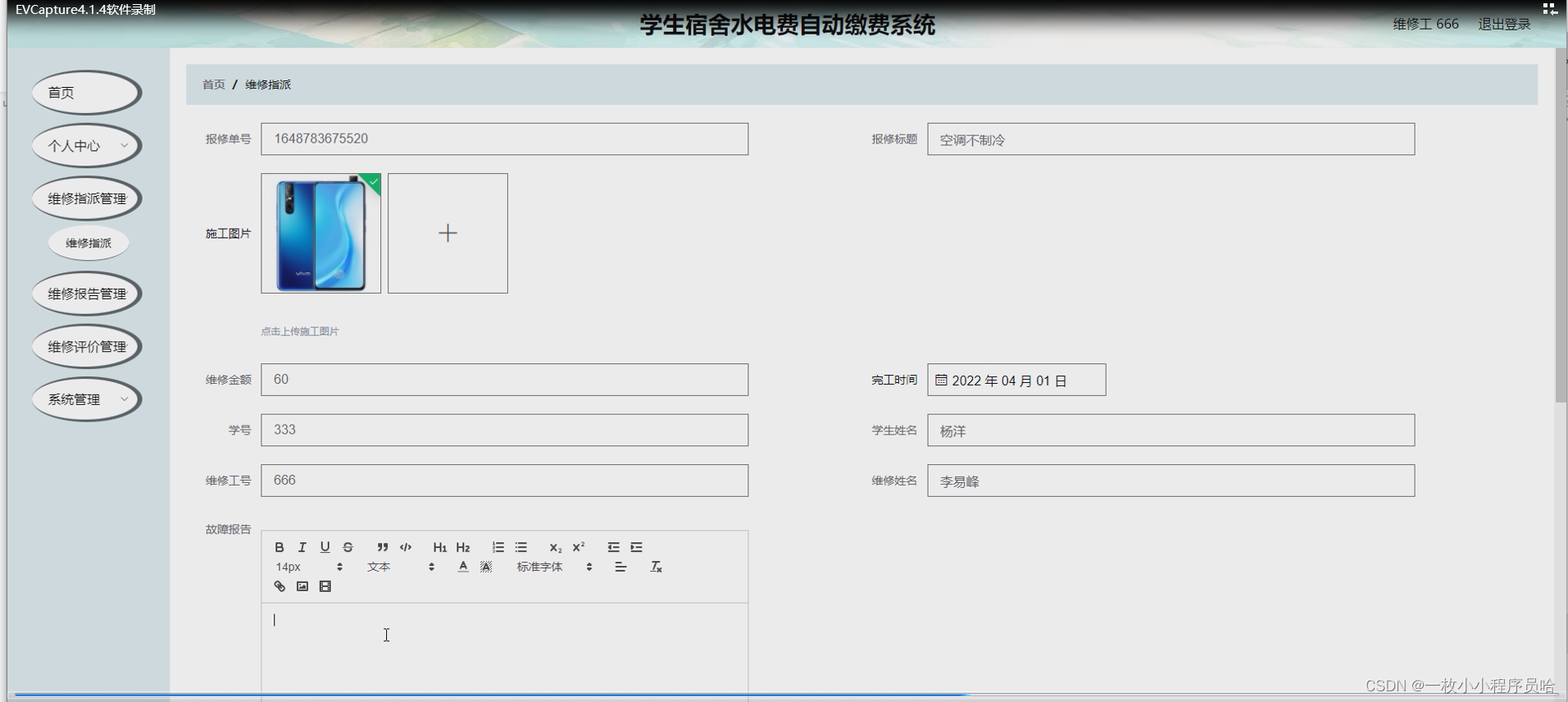
学生宿舍水电费自动缴费系统/基于javaweb的水电缴费系统
摘 要 “互联网”的战略实施后,很多行业的信息化水平都有了很大的提升。但是目前很多学校日常工作仍是通过人工管理的方式进行,需要在各个岗位投入大量的人力进行很多重复性工作,这样就浪费了许多的人力物力,工作效率较低&#x…...

机器人中的数值优化(十三)——QP二次规划
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,…...
语言深入理解指针(非常详细)(三)
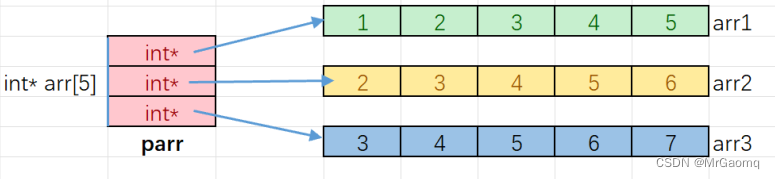
目录 数组名的理解使用指针访问数组 一维数组传参的本质二级指针指针数组指针数组模拟二维数组 数组名的理解 在上⼀个章节我们在使用指针访问数组的内容时,有这样的代码: int arr[10] {1,2,3,4,5,6,7,8,9,10}; int *p &arr[0];这里我们使用 &am…...

实训笔记8.31
实训笔记8.31 8.31笔记一、项目开发流程一共分为七个阶段1.1 数据产生阶段1.2 数据采集存储阶段1.3 数据清洗预处理阶段1.4 数据统计分析阶段1.5 数据迁移导出阶段1.6 数据可视化阶段 二、项目数据清洗预处理的实现2.1 清洗预处理规则2.1.1 数据清洗规则2.1.2 数据预处理规则 2…...

el-table 垂直表头
效果如下: 代码如下: <template><div class"vertical_head"><el-table style"width: 100%" :data"getTblData" :show-header"false"><el-table-columnv-for"(item, index) in getHe…...

B081-Lucene+ElasticSearch
目录 认识全文检索概念lucene原理全文检索的特点常见的全文检索方案 Lucene创建索引导包分析图代码 搜索索引分析图代码 ElasticSearch认识ElasticSearchES与Kibana的安装及使用说明ES相关概念理解和简单增删改查ES查询DSL查询DSL过滤 分词器IK分词器安装测试分词器 文档映射(字…...

机器学习:塑造未来的核心力量
着科技的飞速发展,机器学习已经成为我们生活中不可或缺的一部分。无论是搜索引擎、推荐系统,还是自动驾驶汽车和机器人,都依赖于机器学习算法。本文将探讨机器学习的基本概念、应用领域以及未来发展趋势。 一、机器学习的基本概念 机器学习…...
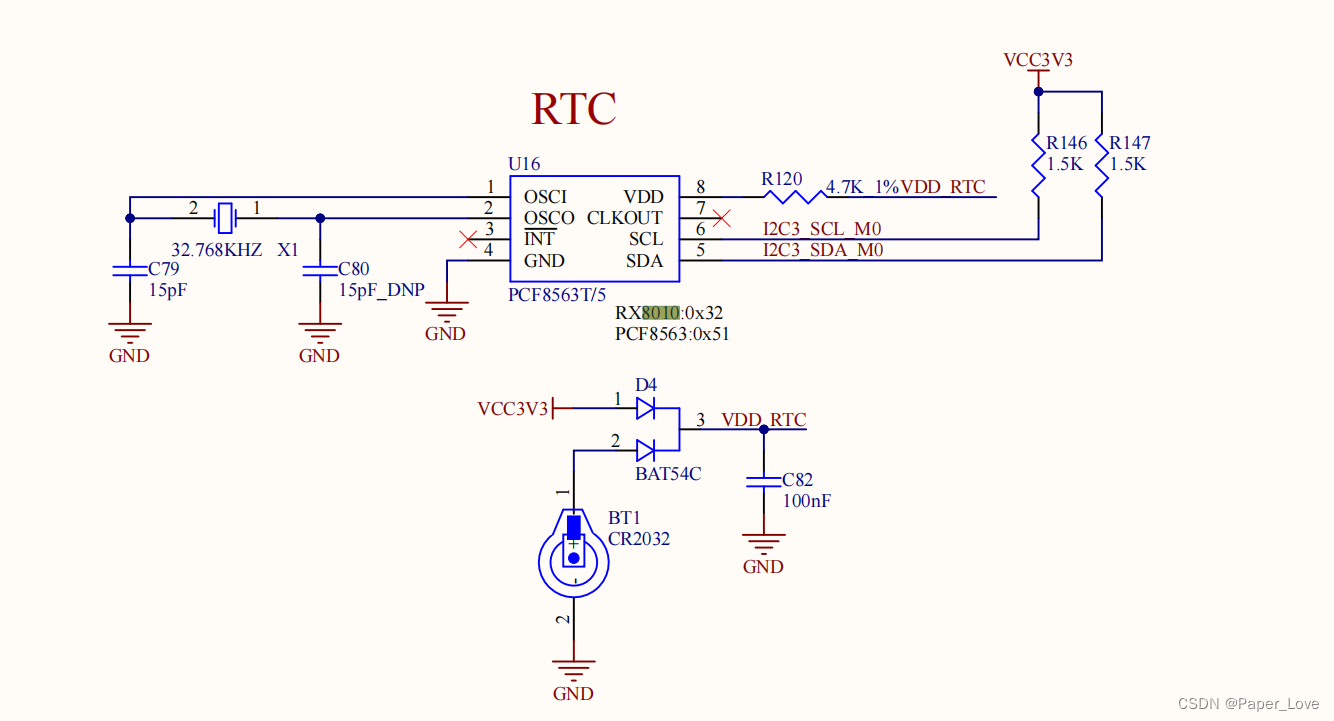
RK3568-i2c-适配8010rtc时钟芯片
硬件连接 从硬件原理图中可以看出,rtc时钟芯片挂载在i2c3总线上,设备地址需要查看芯片数据手册。编写设备树 &i2c3 {status "okay";rx8010: rx801032 {compatible "epson,rx8010";reg <0x32>;}; };使能驱动 /kernel/…...

Spring Security - 基于内存快速demo
基于内存方式 - 只作学习参考1.引入依赖<dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-thymeleaf</artifactId></dependency>2.login.html、index.html、fail.htmllogin.html:<form method…...

6 | 从文本文件中读取单词并输出不重复的单词列表
Transformation 操作 Transformation 操作是用于从一个 RDD(Resilient Distributed Dataset)创建一个新的 RDD,通常是通过对原始 RDD 的元素进行映射、筛选、分组等操作来实现的。Transformation 操作不会立即执行,而是惰性计算,只有在 Action 操作触发时才会真正执行。以…...
配置)
【微信小程序篇】- 多环境(版本)配置
最近自己在尝试使用AIGC写一个小程序,页面、样式、包括交互函数AIGC都能够帮我完成(不过这里有一点问题AIGC的上下文关联性还是有限制,会经常出现对于需求理解跑偏情况,需要不断的重复强调,并纠正错误,才能得到你想要的…...
)
ssh配置(一、GitLabGitHub)
一. 为什么配置ssh 使用 ssh 克隆项目,更加安全方便。 git clone 项目时一般使用两种协议 https 和 ssh 。 二. 原理的通俗解释 ssh 解决的问题是登录时的用户身份验证问题,默认使用 RSA(也支持其他算法: RSA、DSA、ECDSA、EdD…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...
