需求分析入门
认识管理软件
什么是管理软件
管理软件就是用来辅助企业进行管理的软件,既包括对企业“人、财、物”相关的资产信息的管理,也包括对企业“供、产、销”相关的业务活动信息的管理。管理软件的重点在于管理信息的收集、流转,资源的共享、集成,任务的下发、驱动,工作流程的审批、监控,管理决策的支持、验证等。
注意:需要管理的并不仅仅是企业。学校、政府机关等都需要管理。在这里使用“组织”两个字比较准确,但为了表述方便,后面统一称之为“企业”。
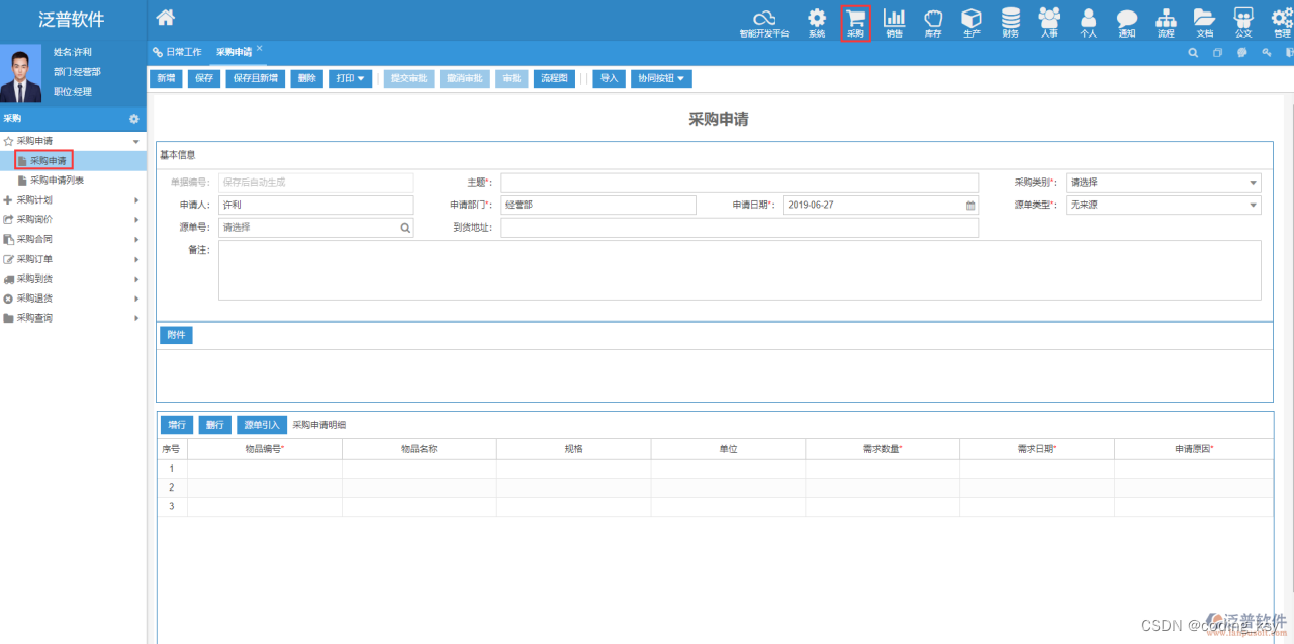
【案例】一款典型的管理软件
认识两个常用的名词:“软件”与“系统”。
软件仅指开发出来的代码,软件在企业中正式使用起来后,才构成系统,也就是说系统不仅包括软件,还包括数据,还包括围绕软件、数据的相关流程、规范。
软件可以复制无数份,而每个系统都是独一无二的。

什么是好管理软件

管理软件的发展
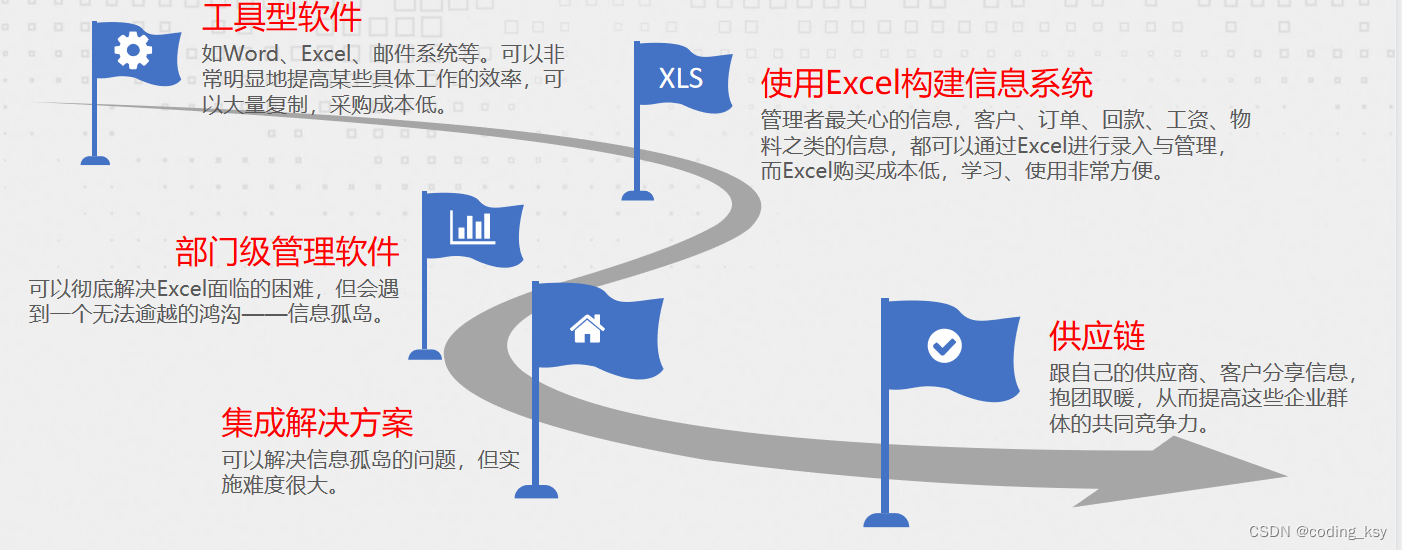 注意:这个过程只是一种行业性的示意过程,并不是说每个企业都一定会经过这些过程,对于具体的企业,使用管理软件的发展过程是由其行业特性、管理方式、管理者思想、地区习惯、竞争对手等各方面因素决定的
注意:这个过程只是一种行业性的示意过程,并不是说每个企业都一定会经过这些过程,对于具体的企业,使用管理软件的发展过程是由其行业特性、管理方式、管理者思想、地区习惯、竞争对手等各方面因素决定的
常用的管理软件
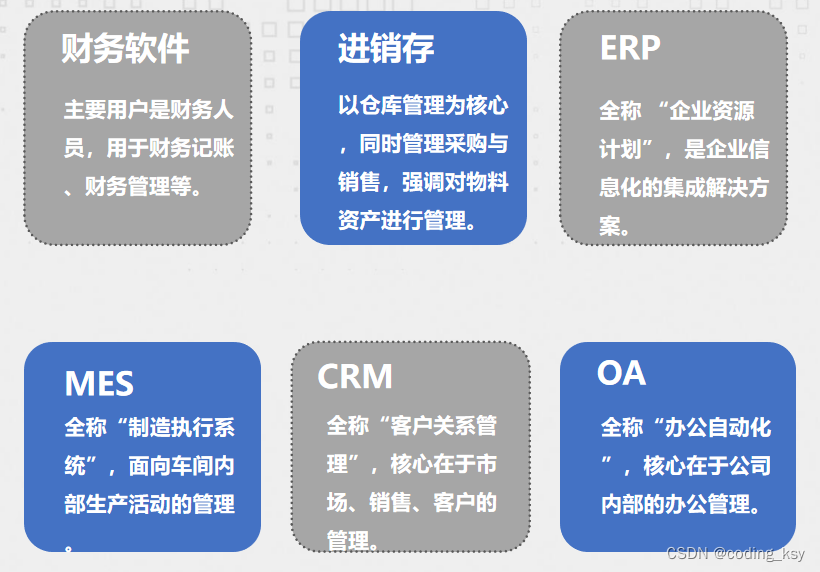 各种业务管理系统
各种业务管理系统
各行各业广泛存在着各种业务管理系统,每个单位都有可能根据自己的要求引进或者开发管理软件。如——
学校:操行记录管理系统
长途运输公司:汽车票销售系统
医院:处方管理系统
公安:暂住证管理系统
管理软件的实施方式

认识需求分析
需求分析的定义
需求分析是软件开发的一个步骤,主要作用是充当软件研发与客户之间的桥梁,工作内容主要包括:
- 对客户的信息化需求进行分析
- 将客户不规范的、随意的需求,转换成规范的、严谨的、结构化的需求
- 将客户不正确的需求转换成正确的需求
- 将客户不切实际的需求转换成可以实现的需求
- 将客户不必要的需求砍掉
- 将客户漏掉的需求补上
举个例子
小王是某软件公司的需求分析师(小王运气不错,接下来,他会成为本书所有案例中的首席需求分析师)。最近公司刚签了一份软件开发合同,需要给一家企业开发一套库存管理系统用以管理该企业原材料、半成品、成品三个仓库的储存物料,小王负责这个项目的需求析工作。在到企业现场之前,他先准备了一份需求调查问卷发给各个仓库保管员与仓库会计,获得答卷后他做了仔细研究,觉得自己对这几个仓库的管理已经有了初步理解。然后他来到企业工作现场,收集了仓库用到的所有单据,如入库单、出库单、验收单等,分析这些单据后他搞清了仓库目前的信息处理情况,然后跟分管仓库的企业副总、物流经理、保管员、仓库会计做了单独的访谈,获得了他们对信息化管理的想法。
需求调研完成后,小王进行了系统规划。有些需求明显超出了项目范围,需要做控制,如副总提出能否在系统中管理生产任务,明显超出了这个库存系统的范围;有些需求,没有人提出来,但为了仓库的信息化管理是必需的,小王建议加进去,如仓库每个月给财务的结存报表,有了系统后明显不应该再由人工做这件事了。经过整理、讨论、沟通、说服等过程后,小王最终跟客户确定了需求。根据确定的需求,小王跟客户讨论确定了未来在信息化管理系统下的管理方式,包括相关人员应该如何工作,各岗位与信息化系统相关的工作职责,使用者的计算机终端如何布置,在什么情况下需要使用软件,等等。
然后小王开始进行软件设计。先根据软件需要处理的信息,以及信息流动的过程,设计了数据模型,确定本系统需要哪些业务实体,每个实体包括哪些属性,各个实体之间的关系等:然后,进行功能建模,确定需要提供哪些功能点,每个功能点包括哪些子功能,每个功能的业务规则等;接下来,使用一款原型设计工具进行软件功能界面的设计,在设计的过程中,安排时间给相关用户讲解自己的设计思想,告诉用户在工作过程中需要如何使用本软件,一边听取用户的意见,一边修改;另外,遇到一些技术上不容易实现的地方,还会征求开发人员的意见,经过几次外部、内部评审会后定稿了;最后,根据设计成果撰写了原型说明书。小王将数据模型、界面原型、原型说明书交给研发部门据以开发。软件开发完成上线后,用户提出有些功能不符合管理要求,需要修改,提出了需求变更要求,小王根据用户要求设计了需求变更解决方案,撰写了需求变更说明书,交给研发部门修改软件。
需求的获取方法
需求获取就是通过需求调研获取用户对信息化的需求。常用的需求调研方式包括:
-
观察法
-
体验法
-
问卷调查法
-
访谈法
-
单据分析法
-
报表分析法
-
需求调研会法
系统规划
系统规划的过程就是根据用户的需求规划企业的信息化管理体系的过程。
主要包括三个步骤:
- 需求确定
- 整理需求
- 设计系统蓝图
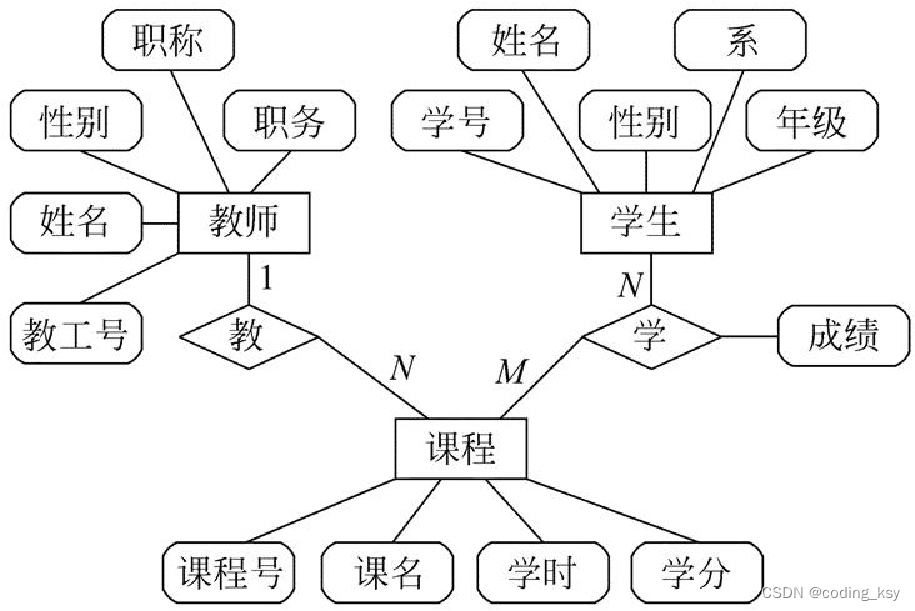
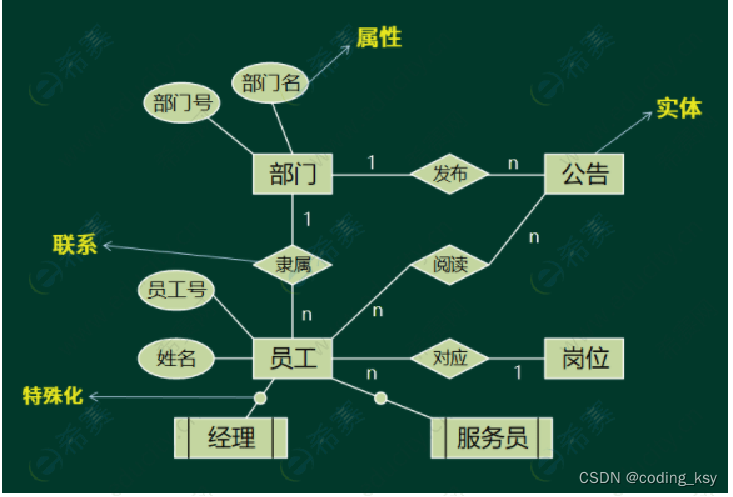
数据建模
数据建模就是设计数据库的表结构,这项工作可以在功能设计之前,也可以在功能设计之后,也可以同时进行,不同的团队有不同的工作方式。一般来说,越是复杂、大型的系统,数据建模工作越重要,也越应该尽早进行。良好的数据库结构可以让数据流清晰,可以降低功能设计与开发的难度,特别是一旦发生了需求变更,可以灵活应对。对软件开发有点经验的人都知道,一旦软件投入使用,修改数据库结构是非常致命的。
数据建模需要考虑——
- 实体关系
- 范式
- 表
- 表的关系
- 字段
参考文献
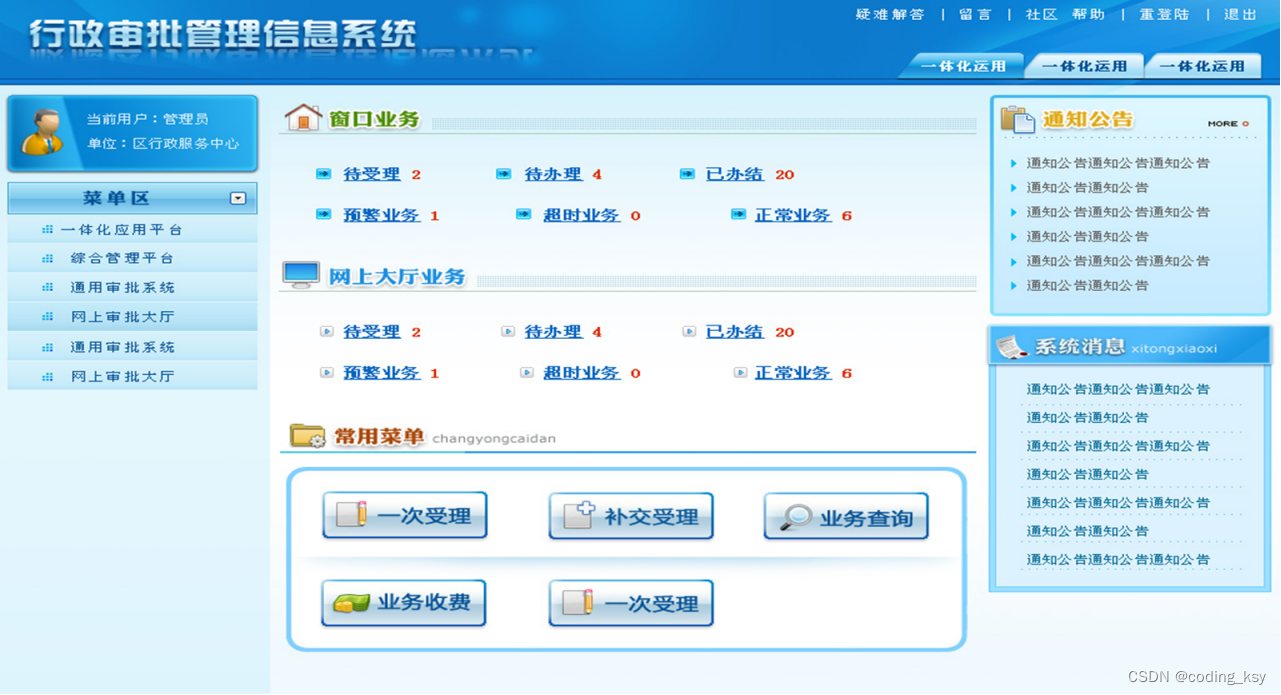
功能设计
软件的功能,从本质上说就是对数据进行输入、加工、输出的过程。对于面向数据库的软件,由于是以数据库为核心的,可以理解为两个方面:
一是数据的收集与处理;
二是围绕数据库对其中的数据进行的四大操作,即增、删、改、查
功能建模,指根据系统规划的要求设计:
系统由哪些功能构成
每个功能应该输入什么
经过功能处理后应该输出什么
每个功能又包括哪些子功能,不断分解下去,直到最底层
原型说明书
原型说明书是针对设计好的软件原型撰写的一种偏向于说明功能与操作逻辑的文档,主要描述——
- 每个功能点的主要用户
- 用户使用该原型的操作场景
- 有什么权限控制要求
- 每个操作背后是怎么运算的
- 对数据有什么要求
需求变更
需求变更伴随着软件的整个生命周期。有些需求变更处理起来非常简单,影响面小,工作量也小,而有些需求变更处理起来非常麻烦,伤筋动骨,工作量巨大。
在软件的各个阶段都有可能发生需求变更。
需求变更发生得越早,解决起来代价就越小。
作为设计人员,要尽力降低需求变更的可能性,但对需求变更也要有个清醒的认识,就是需求变更是无法回避的,犯不着怨天尤人,面对需求变更需要有个积极良好的心态,毕竟有时候需求变更也未必就是坏事。
如何成为一个需求分析师
什么是需求分析师
需求分析师包括以下工作职责:
进行需求调研,获取用户需求;
- 进行系统规划,设计客户信息化管理的蓝图;
- 设计数据模型;
- 设计软件功能;
- 设计软件界面,绘制软件原型;
- 召开需求评审会,收集各方面的意见,根据意见修改设计;
- 指导开发,协助测试;
- 进行软件变更需求分析,设计变更解决方案。
性格要求
掌握IT知识
需求分析师需要掌握的IT知识:
- 软件工程理论
- 项目管理理论
- 关系数据库
- 软件文档
- 办公工具
- 编程语言
- 网络与硬件
- 软件架构
- 云计算
- 软件界面
掌握企业管理知识
需求分析师需要掌握的企业管理知识:
- 企业运作流程
- 财务会计
- 采购
- 销售
- 库存
- 生产
- 计划
- 成本
- 质量
- 人力资源
- 组织
精通一种开发模型
本书介绍“快速原型”开发模型,这是开发中小型管理软件的最佳模型。“快速原型”开发模型大概步骤如下:
- 通过各种方式理解客户业务,获得客户需求。
- 根据客户的业务流程,管理方式,以及客户对信息化的需求进行系统规划。
- 根据规划结果设计数据库。
- 根据规划结果设计软件功能。
- 根据规划结果设计原型界面。
- 撰写原型说明书。
- 需求评审。
- 根据评审结果修改设计。
- 开发、测试。
- 内部试用软件,发现问题,改善软件。
- 用户试用软件,发现问题,改善软件。
- 软件上线,进入维护期,应对需求追加与变更,促使软件不断成长。
软件需求分析实战》,清华大学出版社出版,作者杨长春
相关文章:

需求分析入门
认识管理软件 什么是管理软件 管理软件就是用来辅助企业进行管理的软件,既包括对企业“人、财、物”相关的资产信息的管理,也包括对企业“供、产、销”相关的业务活动信息的管理。管理软件的重点在于管理信息的收集、流转,资源的共享、集成…...

攻防世界-php_rce
原题 解题思路 thinkPHP.0有漏洞,ThinkPHP5.x rec 漏洞分析与复现。本题就是利用漏洞查找。格式是: ?sindex/\think\app/invokefunction&functioncall_user_func_array&vars[0]system&vars[1][]命令。 ls查看文件没什么东西,r…...
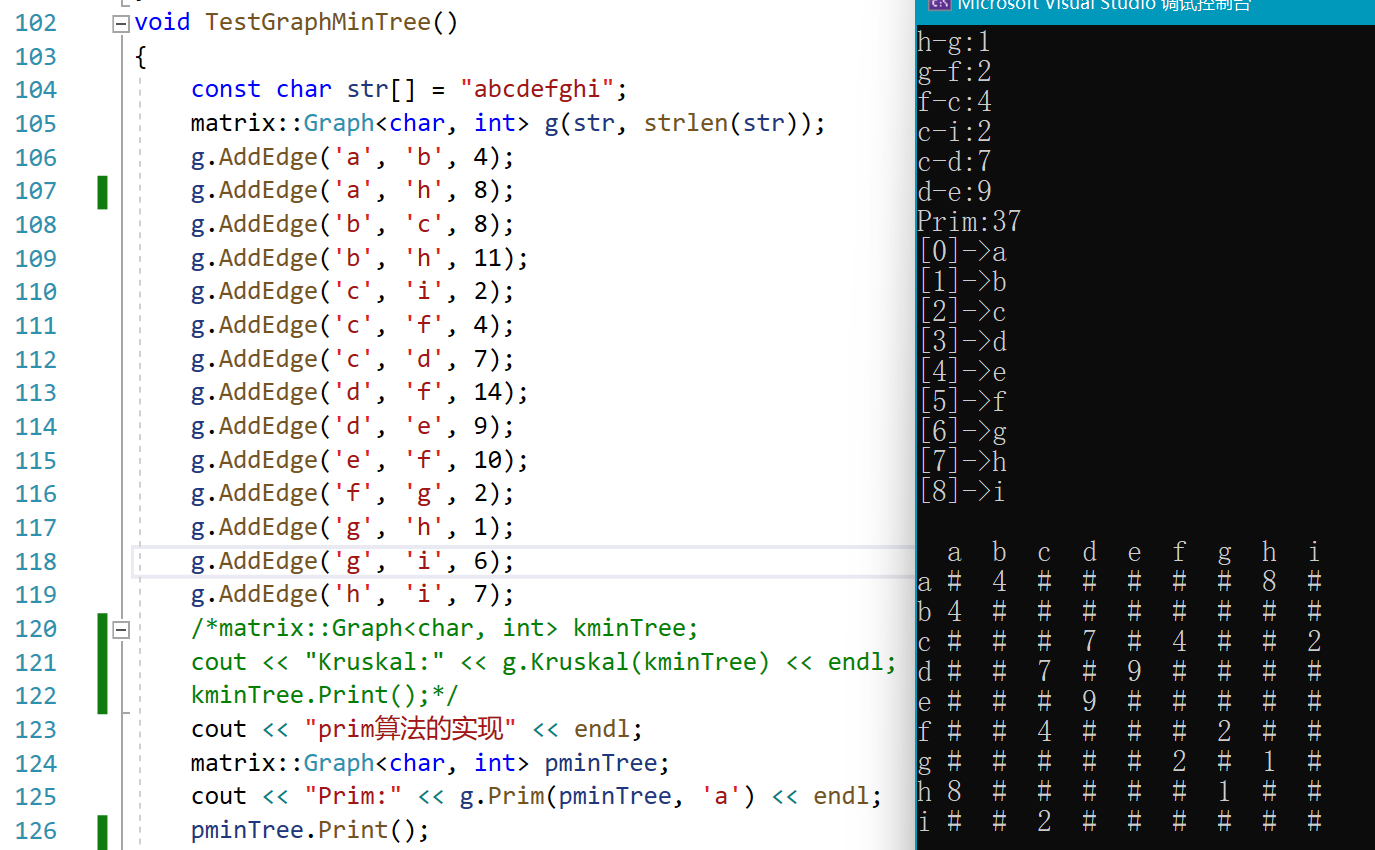
最小生成树Kruskal、Prim算法C++
什么是最小生成树 连通图: 在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1和顶点v2是连通的。如果图中任意一对顶点都是连通的,则称此图为连通图。 生成树: 一个连通图的最小连通子图称作为图的生成树。有n个顶点的…...

系统架构设计师-计算机系统基础知识(2)
目录 一、存储管理 1、页式存储 2、段式存储 3、段页式存储 二、磁盘管理 1、先来先服务FCFS 2、最短寻道时间优先SSTF 三、文件系统 1、文件基本概念 2、文件的类型: 3、索引文件结构 4、位示图 四、性能指标 五、性能设计 1、阿姆达尔定律 六、性能评估 1、…...
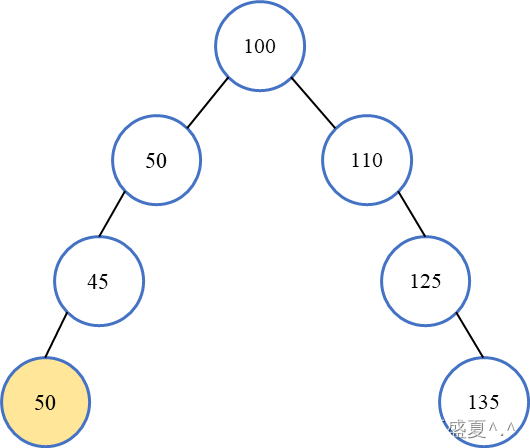
二叉树的介绍
写在前面: 二叉树是数据结构课程中非常重要的内容,我们针对二叉树的概念、性质以及类型展开详细介绍。 一、概念 二叉树(Binary Tree)是n(n>0)个结点的有限集合,该集合或者空集࿰…...
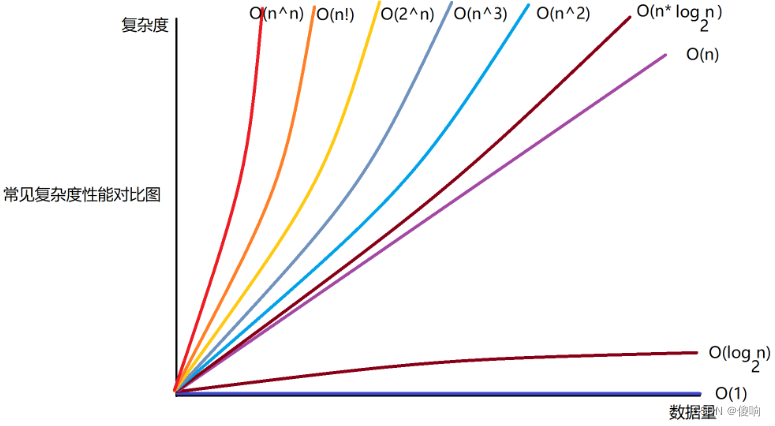
数据结构与算法复杂度介绍
目录 一、基本概念 二、时间复杂度 【2.1】时间复杂度概念 【2.2】大O的渐进表示法 【2.3】举例时间复杂度计算 三、空间复杂度 一、基本概念 数据结构:相互之间存在一种或者多种特定关系的数据元素的集合。在逻辑上可以分为线性结构,散列结构、树…...

CentOS 安装蒲公英
官方教程链接: https://service.oray.com/question/5063.html 教程使用的是2.3版本,官网下载的最新版是2.4,所以命令会有所不同 安装成功后, 任意路径下执行pgyvisitor,调出交互界面pgyvisitor login,登录…...

英语语法基础--思维导图
思维导图通常用于可视化和整理信息,而英文语法非常广泛且复杂,无法在一个简单的思维导图中完整表示。然而,我可以提供一个简化版本的英文语法思维导图,列出一些主要的语法概念和部分示例。 请注意,这只是一个基本的概…...

Android泛型详解
参考文献:https://pingfangx.github.io/java-tutorials/java/generics/types.html 1,什么是泛型? Java泛型(generics)是JDK5中引入的一个新特性,泛型提供了 编译时类型安全检测机制, 该机制允许程序员在编译时检测到…...
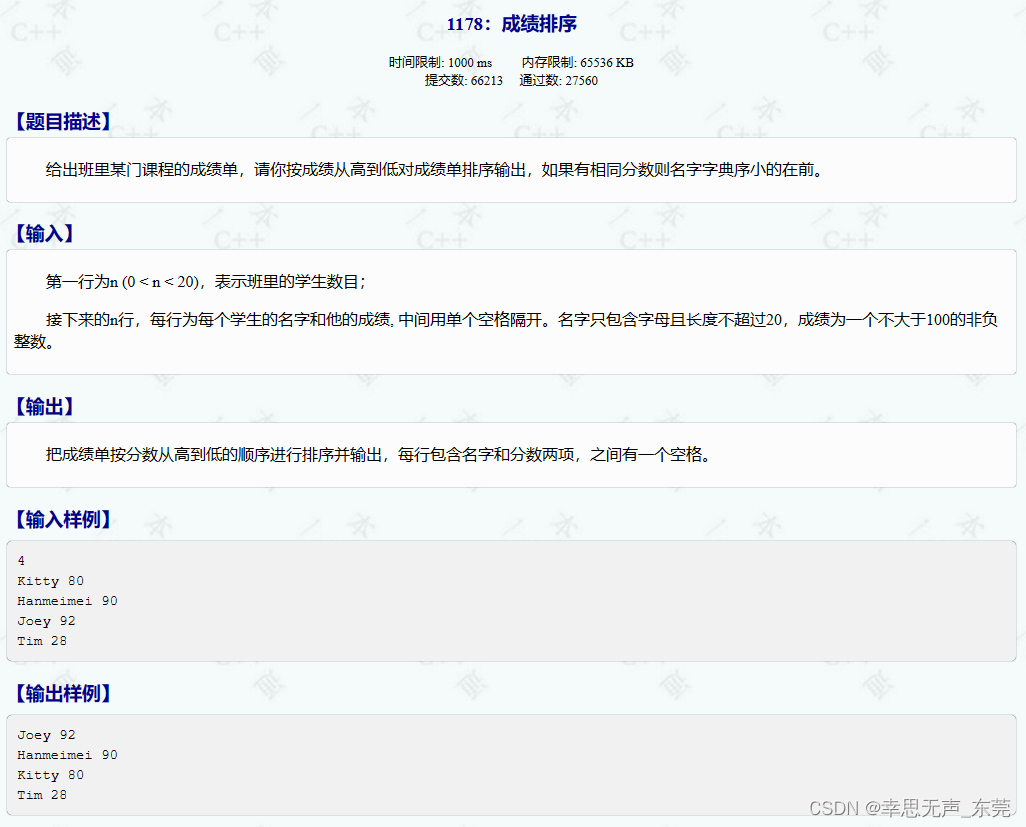
C++信息学奥赛1178:成绩排序
#include<bits/stdc.h> using namespace std; int main(){int n;cin>>n; // 输入整数 n,表示数组的大小int arr[n]; // 创建大小为 n 的整型数组 arrstring brr[n]; // 创建大小为 n 的字符串数组 brrfor(int i0;i<n;i) cin>>brr[i]>>ar…...
)
【计算机视觉 | 目标检测】目标检测常用数据集及其介绍(七)
文章目录 一、Cops-Ref二、FAT (Falling Things)三、GEN1 Detection (Prophesee GEN1 Automotive Detection Dataset)四、RIT-18五、AGAR (Annotated Germs for Automated Recognition)六、EuroCity Persons七、Freiburg Groceries八、Lytro Illum九、PFN-PIC (PFN Picking Ins…...

100天精通Golang(基础入门篇)——第20天:Golang 接口 深度解析☞从基础到高级
🌷🍁 博主猫头虎🐅🐾 带您进入 Golang 语言的新世界✨✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文并茂…...

ESXi 6.7添加螃蟹2.5g网卡支持
安装了ESXi 6.7,结果机器两块网卡只能识别一块,然后想着不能让另一块浪费啊,开始折腾,看着网上都是找的驱动然后封装进iso,可是我已经装完了,怎么办,然后找到了下面解决方法 1.找驱动 下载RTL81…...

机器学习笔记之最优化理论与方法(四) 凸函数:定义与基本性质
机器学习笔记之最优化理论与方法——再回首:凸函数定义与基本性质 引言凸函数的定义严格凸函数凸函数的推论:凹函数 常见凸函数凸函数的基本性质几种保持函数凸性的运算凸集与凸函数之间的关联关系 引言 本节将介绍凸函数定义及其基本性质。 本文是关于…...

【Git】git tag 查看版本号 | 删除本地 | 删除远程仓库| 批量删除
一、删除指定tag 使用场景:比如我们在本地git tag了一个错误的版本号,但是还没有push,想直接删掉避免污染远程仓库 1、删除指令 要删除指定的Git标签(版本号),您可以使用以下命令: git tag -d 标…...
)
thinkphp:数据库查询,嵌套别的表的查询(别的表做子查询)
例子 从 vendors 表中选择记录。在 vendors 表中,筛选出具有满足以下条件的 vendor_code 值: 对应的采购订单(在 po_headers_all 表中)存在未完全接收的采购行(在 po_lines_all 表中)。相应的采购订单状态…...

《Linux 系统命令及Shell脚本实践指南》
Linux 系统命令及Shell脚本实践指南 《Linux 系统命令及Shell脚本实践指南》该书从结构上分为三部分:第一部分1.1Linux的历史发展1.2用户管理1.3任务管理单一时刻执行一次任务使用at周期性任务使用:cron表达式,命令crontab 1.4文件管理1.4.1 Linux shell…...

代码随想录算法训练营第三十八天 | ● 理论基础 ● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
题目链接:509. 斐波那契数 代码随想录 视频:手把手带你入门动态规划 | LeetCode:509.斐波那契数_哔哩哔哩_bilibili 看完代码随想录之后的想法: 我们要知道动态规划的五部曲; 1,确定dp数组的含义&#x…...
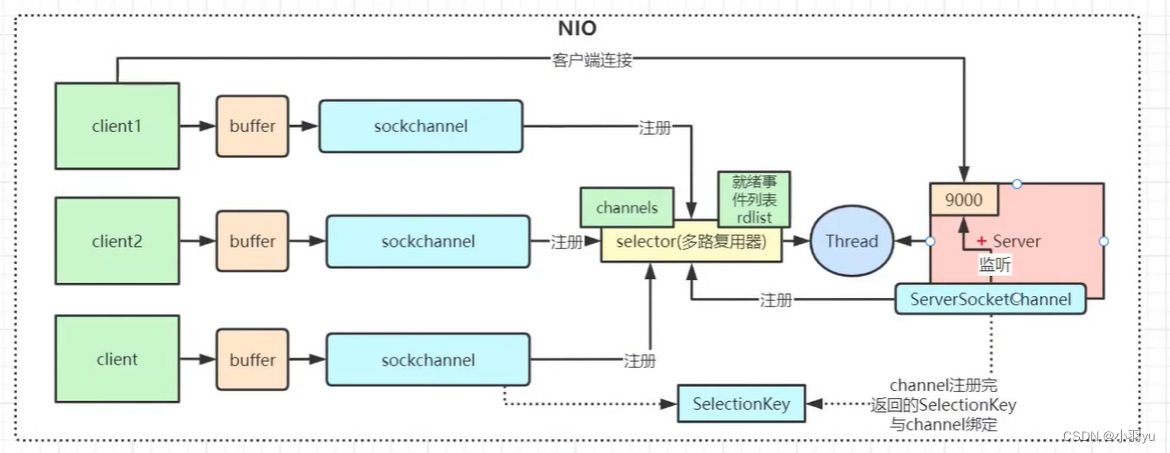
Java分别用BIO、NIO实现简单的客户端服务器通信
分别用BIO、NIO实现客户端服务器通信 BIONIONIO演示(无Selector)NIO演示(Selector) 前言: Java I/O模型发展以及Netty网络模型的设计思想 BIO Java BIO是Java平台上的BIO(Blocking I/O)模型&a…...

React Portals
什么是React Portals React Portals(React 门户)是 React 提供的一种机制,用于将组件渲染到 DOM 树中的不同位置,而不受组件层次结构的限制。它允许你将一个组件的渲染内容“传送”到 DOM 结构中的任何位置,通常用于处…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
