安全错误攻击
近年来基于错误的密码分析(fault-based cryptanalysis)已成为检测智能卡(Smartcard)安全的重要因素。这种基于错误的密码分析,假设攻击者可以向智能卡中导入一定数量的、某种类型的错误,那么智能卡会输出错误的信息,攻击者有可能利用这些错误信息揭露出嵌入在智能卡中的秘密参数(如密钥)。为此,一些研究者提出了通过检验计算结果的正确性来防止这种攻击,即如果检验结果不正确,那么拒绝输出,从而使攻击者无法得到想要的错误信息。
然而,仅通过检验计算结果来防止这种攻击的方法不可行。以RSA中模指数运算为例,提出了一种所谓基于安全错误的对RSA的攻击。该攻击可以攻破RSA的一些实现算法,即使那些算法中加入了检验计算结果的步骤。
密码实现
RSA 算法中经常用到的是模幂运算 M d m o d N M^d\mod N MdmodN。其中将私钥表达成二进制的形式,即, d = ∑ i = 0 n − 1 d i 2 i , d i ∈ { 0 , 1 } d = \sum_{i=0}^{n-1}d_i 2^i, d_i\in\{0,1\} d=∑i=0n−1di2i,di∈{0,1}。从而在密码芯片中对应R-L比特算法实现。
在算法1中,当 d i = 1 d_i = 1 di=1 时,算法执行一次模乘运算( A ⋅ B 2 m o d N A\cdot B^2\mod N A⋅B2modN)和一次摸平方运算( B 2 m o d N B^2\mod N B2modN)。当 d i = 0 d_i=0 di=0时,算法只需执行一次摸平方运算。
其中,RSA 用到模乘运算 R = A ⋅ B m o d N R = A\cdot B \mod N R=A⋅BmodN。将A表达成 2 t 2^t 2t进制的形式, A = ∑ j = 0 m − 1 A j ( 2 t ) j A j ∈ { 0 , 1 , ⋯ , 2 t − 1 } , m = ⌈ n / t ⌉ A = \sum_{j=0}^{m-1}A_j(2^t)^j A_j\in\{0,1,\cdots,2^t-1\},m=\lceil n/t \rceil A=∑j=0m−1Aj(2t)jAj∈{0,1,⋯,2t−1},m=⌈n/t⌉。则 模乘运算的结果 R R R 可用以下表达式来实现。
R = ( ( ⋯ ( ( A m − 1 B ) 2 t + A m − 2 B ) 2 t + ⋯ + A 1 B ) 2 t + A 0 B ) m o d N R =((\cdots( (A_{m-1}B)2^t + A_{m-2}B)2^t+\cdots + A_1B)2^t + A_0B) \mod N R=((⋯((Am−1B)2t+Am−2B)2t+⋯+A1B)2t+A0B)modN
算法1 R-L 比特模幂
输入: M M M, d = ( d n − 1 , ⋯ , d 0 ) 2 d = (d_{n-1},\cdots ,d_0)_2 d=(dn−1,⋯,d0)2, N N N
输出: A = M d m o d N A = M^d \mod N A=MdmodN
1.1 A ⟵ 1 A \longleftarrow 1 A⟵1; B ⟵ M B \longleftarrow M B⟵M
1.2 for i i i from 0 0 0 to n − 1 n-1 n−1
1.3 if ( d i = 1 d_i=1 di=1) then A ⟵ A ⋅ B m o d N A \longleftarrow A\cdot B \mod N A⟵A⋅BmodN
1.4 B ⟵ B 2 m o d N B \longleftarrow B^2 \mod N B⟵B2modN
1.5 endfor
算法2 底数为 2 t 2^t 2t的模乘运算
输入: A , B , N A,B,N A,B,N
输出: R = A ⋅ B m o d N R = A\cdot B \mod N R=A⋅BmodN
2.1 R ⟵ 0 R \longleftarrow 0 R⟵0
2.2 for j j j from m − 1 m-1 m−1 downto 0 0 0
2.3 R ⟵ ( R 2 t + A j B ) m o d N R \longleftarrow (R2^t + A_j B)\mod N R⟵(R2t+AjB)modN
2.4 endfor
将算法1和算法2合并起来,那么R-L比特模幂运算可写成如下实现过程。
算法3
输入: M M M, d = ( d n − 1 , ⋯ , d 0 ) 2 d = (d_{n-1},\cdots ,d_0)_2 d=(dn−1,⋯,d0)2, N N N
输出: A = M d m o d N A = M^d \mod N A=MdmodN
3.1 A ⟵ 1 A \longleftarrow 1 A⟵1; B ⟵ M B \longleftarrow M B⟵M
3.2 for i i i from 0 0 0 to n − 1 n-1 n−1
3.3 if ( d i = 1 d_i=1 di=1) then
3.4 R ⟵ 0 R \longleftarrow 0 R⟵0
3.5 for j j j from m − 1 m-1 m−1 downto 0 0 0
3.6 R ⟵ ( R 2 t + A j B ) m o d N R \longleftarrow (R2^t + A_j B)\mod N R⟵(R2t+AjB)modN
3.7 endfor
3.8 A ⟵ R A \longleftarrow R A⟵R
3.9 endif
3.10 R ⟵ 0 R \longleftarrow 0 R⟵0
3.11 for j j j from m − 1 m-1 m−1 downto 0 0 0
3.12 R ⟵ ( R 2 t + A j B ) m o d N R \longleftarrow (R2^t + A_j B)\mod N R⟵(R2t+AjB)modN
3.13 endfor
3.14 B ⟵ R B \longleftarrow R B⟵R
3.15 endfor
基于安全错误的攻击
考虑针对算法3进行攻击,攻击者攻击目的是要找到运算中隐藏着的密钥 d d d。
所谓安全错误,是指在算法中导入1比特或几比特错误,但这一错误可能并不会影响最终的模幂运算结果。
例如,在 d i = 1 d_i = 1 di=1时的第 i i i 次循环中,向寄存器 A k A_k Ak 中导入错误,且满足 k > j k > j k>j,那么,由于正确的 A k A_k Ak 在先前的子循环中已经使用了,所以算法三第3步的子循环不会计算出错,即, R R R计算正确。而紧接着 A ⟵ R A \longleftarrow R A⟵R使得先前导入的错误被清除。于是算法三在以下的计算都不会受到影响。从而使得最终的计算结果是正确的。把这样导入的错误称之为安全错误。换言之,安全错误发生了却并没有带来错误的计算结果。
但是,导入的安全错误并不总是安全的。在一些情况下安全错误也会使得计算结果不正确。例如,在 d i = 0 d_i=0 di=0的第 i i i次循环中,向 A k A_k Ak 中导入错误,且满足 k > j k > j k>j,这时导入的错误就会使得最后的计算结果出错。因为,当 d i = 0 d_i=0 di=0时,整个循环将跳过第3步,从而使得导入的错误不能得到纠正,并带入到下面的循环中。
通过上面分析得到以下结论。当 d i = 1 d_i = 1 di=1时,导入的安全错误不会影响计算结果的正确性;当 d i = 0 d_i=0 di=0时,导入的安全错误会使得计算结果不正确。
基于以上的分析,攻击者分别对 d d d的每一位 d i d_i di进行攻击。为了攻击第 i i i 比特,在算法第 i i i次循环中导入安全错误。如果算法三输出正确结果,那么由以上分析,得 d i = 1 d_i=1 di=1;如果算法三输出错误结果,或者算法三通过附加的检测出计算结果错误,从而拒绝输出,那么攻击者可知 d i = 0 d_i=0 di=0。
这就是说,即是智能卡检测出错误,并拒绝输出,攻击者仍可利用这一点得到 d i d_i di 的值。所以说,对算法三实现模幂运算,通过检验计算结果的方式不能防止基于安全错误的攻击。但,通过加指数掩码,每一次进行模幂运算时,在指数 d d d上增加随机数,可防止该攻击。
相关文章:

安全错误攻击
近年来基于错误的密码分析(fault-based cryptanalysis)已成为检测智能卡(Smartcard)安全的重要因素。这种基于错误的密码分析,假设攻击者可以向智能卡中导入一定数量的、某种类型的错误,那么智能卡会输出错…...
logstash配置语法详解)
ELK安装、部署、调试 (八)logstash配置语法详解
input {#输入插件 }filter {#过滤插件 }output {#输出插件 } 1.读取文件。 使用filewatch的ruby gem库来监听文件变化,并通过.sincedb的数据库文件记录被监听日志we年的读取进度(时间 搓) 。sincedb数据文件的默认路径为<path.data>/…...
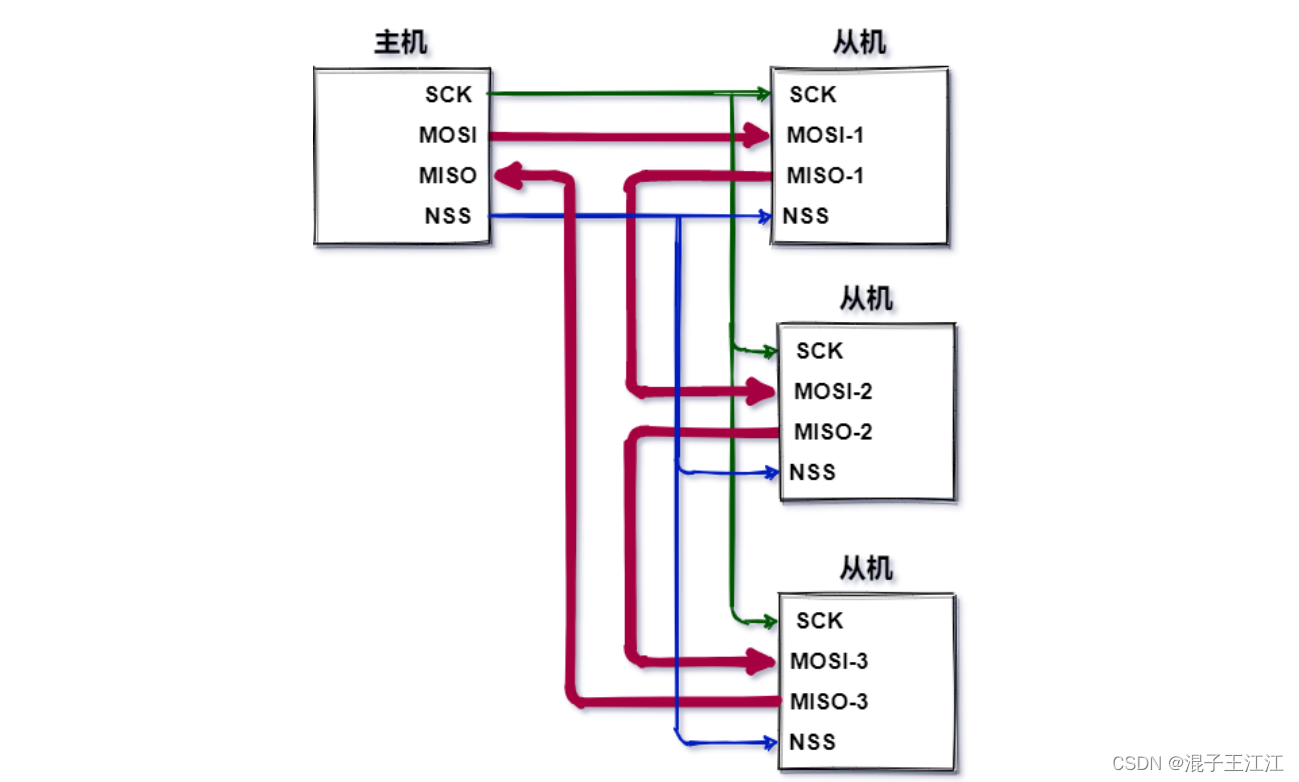
SPI协议
文章目录 前言一、简介1、通信模式2、总线定义3、SPI通信结构4、SPI通讯时序5、SPI数据交互过程 二、多从机模式1、多NSS2、菊花链3、SPI通信优缺点4、UART、IIC、SPI 区别 三、总结四、参考资料 前言 SPI协议是我们的重要通信协议之一,我们需要掌握牢靠。 一、简介…...

机器学习算法系列————决策树(二)
1.什么是决策树 用于解决分类问题的一种算法。 左边是属性,右边是标签。 属性选择时用什么度量,分别是信息熵和基尼系数。 这里能够做出来特征的区分。 下图为基尼系数为例进行计算。 下面两张图是对婚姻和年收入的详细计算过程(为GINI系…...

ACM中的数论
ACM中的数论是计算机科学领域中的一个重要分支,它主要研究整数的性质、运算规律和它们之间的关系。在ACM竞赛中,数论问题经常出现,因此掌握一定的数论知识对于参加ACM竞赛的选手来说是非常重要的。本文将介绍一些常见的数论概念和方法&#x…...
我的创作纪念日 —— 一年之期
前言 大家好!我是荔枝嘿~看到官方私信才发现原来时间又过去了一年,荔枝也在CSDN中创作满一年啦,虽然中间因为种种原因并没有经常输出博文哈哈,但荔枝一直在坚持创作嘿嘿。记得去年的同一时间我也同样写了一篇总结文哈哈哈&#x…...
qt.qpa.plugin:找不到Qt平台插件“wayland“|| (下载插件)Ubuntu上解决方案
相信大家也都知道这个地方应该做什么,当然是下载这个qt平台的插件wayland,但是很多人可能不知道怎么下载这个插件。 那么我现在要说的这个方法就是针对这种的。 sudo apt install qtwayland5完事儿了奥兄弟们。 看看效果 正常了奥。...

详解Spring Boot中@PostConstruct的使用
PostConstruct 在Java中,PostConstruct是一个注解,通常用于标记一个方法,它表示该方法在类实例化之后(通过构造函数创建对象之后)立即执行。 加上PostConstruct注解的方法会在对象的所有依赖项都已经注入完成之后执行…...

判断子序列
判断子序列 题目: 给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"…...
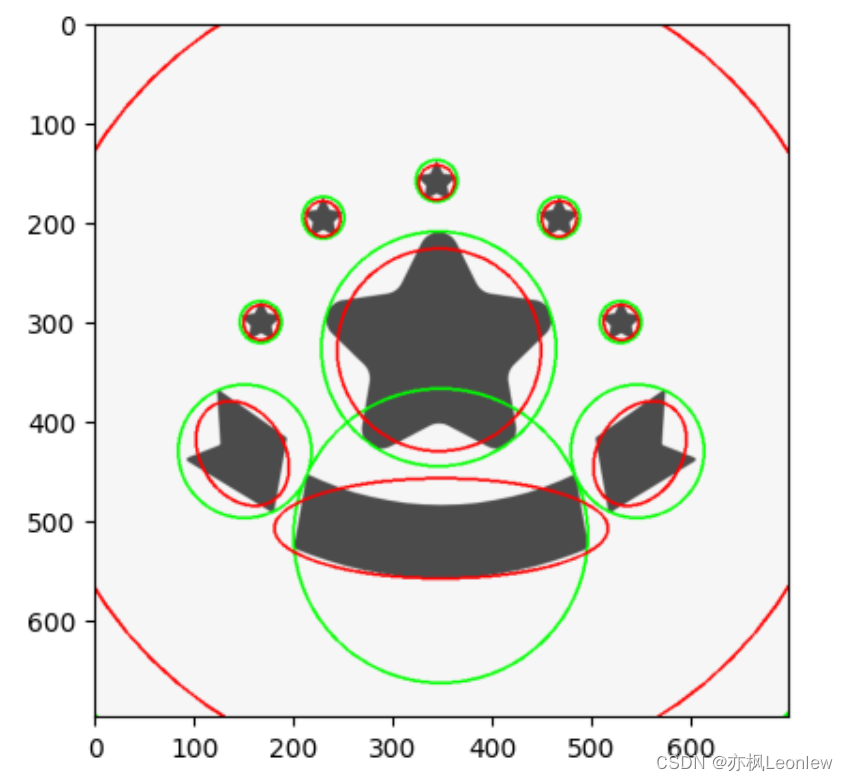
Python Opencv实践 - 轮廓特征(最小外接圆,椭圆拟合)
import cv2 as cv import numpy as np import matplotlib.pyplot as pltimg cv.imread("../SampleImages/stars.PNG") plt.imshow(img[:,:,::-1])#轮廓检测 img_gray cv.cvtColor(img, cv.COLOR_BGR2GRAY) ret,thresh cv.threshold(img_gray, 127, 255, 0) contou…...

Ubuntu22.04 LTS+NVIDIA 4090+Cuda12.1+cudnn8.8.1
系统环境中: 1.系统驱动安装的是: NVIDIA-Linux-x86_64-530.30.02.run 2.CUDA安装:cuda_12.1.0_530.30.02_linux.run(无需第1步,直接安装它就带配套驱动) wget https://developer.download.nvidia.com/…...
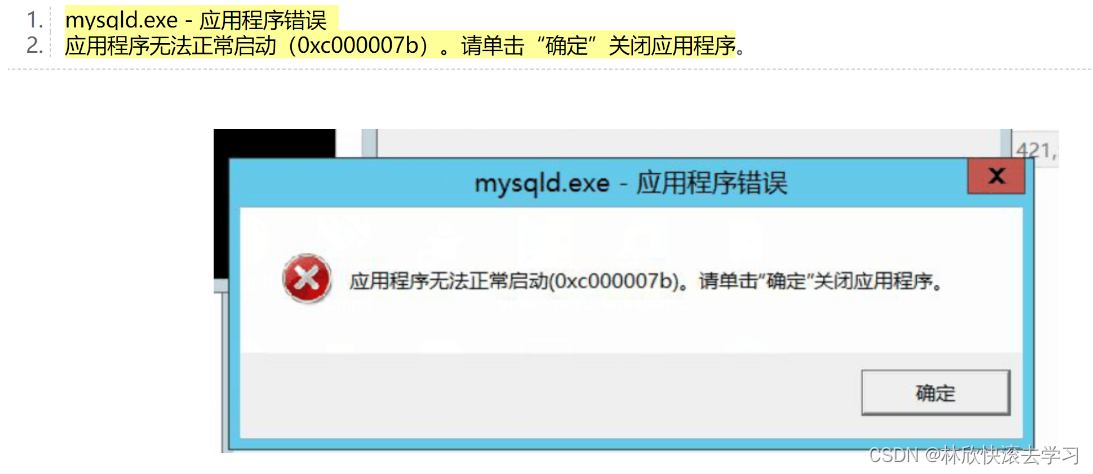
重装系统后,MySQL install错误,找不到dll文件,或者应用程序错误
文章目录 1.找不到某某dll文件2.mysqld.exe - 应用程序错误使用DX工具直接修复 1.找不到某某dll文件 由于找不到VCRUNTIME140_1.dll或者MSVCP120.dll,无法继续执行代码,重新安装程序可能会解决此问题。 在使用一台重装系统过的电脑,再次重新…...
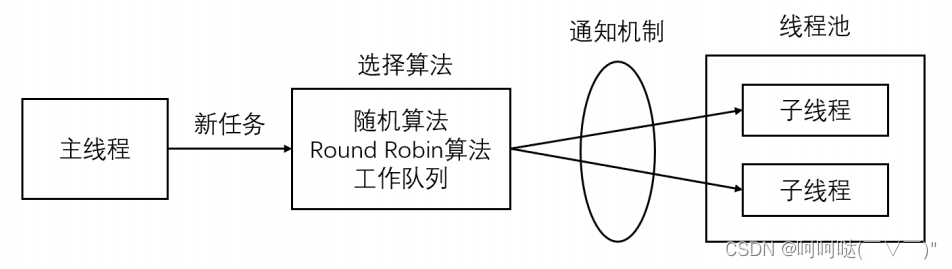
线程同步机制类封装及线程池实现
1.线程池 线程池是由服务器预先创建的一组子线程,线程池中的线程数量应该和 CPU 数量差不多。线程池中的所有子线程都运行着相同的代码。当有新的任务到来时,主线程将通过某种方式选择线程池中的某一个子线程来为之服务。相比与动态的创建子线程&#x…...

Linux中的用户、组和权限
一,Linux的安全模型 1.安全3A Authentication(认证),Authorization(授权),Accounting(审计)(AAA)是用于对计算机资源的访问、策略执行、审计使用情况和提供服务账单所需信息等功能进行智能控制的基本组件的一个术语。大多数人认为这三个组合的过程对有效的网络管理和…...

python学习--基本数据类型之字典
python中数据类型 第一类:不可变类型、静态数据类型、不支持增删改操作 数字(number)字符串(string)元组(tuple) 第二类:可变类型、动态数据类型、支持增删改操作 列表ÿ…...
【OpenCV入门】第九部分——模板匹配
文章结构 模板匹配方法单模板匹配单目标匹配多目标匹配 多模板匹配 模板匹配方法 模板是被查找的图像。模板匹配是指查找模板在原始图像中的哪个位置的过程。 result cv2.matchTemplate(image, templ, method, mask)image: 原始图像templ: 模板图像&a…...

在设计web页面时,为移动端设计一套页面,PC端设计一套页面,并且能自动根据设备类型来选择是用移动端的页面还是PC端的页面。
响应式设计,即移动端和PC端共用一个HTML模式,网站的程序和模板自动根据设备类型和屏幕大小进行自适应调整。这种方法我不喜欢,原因是不能很好保证各种客户端的效果,里面存在各种复杂的兼容性等问题。 我喜欢为不同的客户端写不同的…...
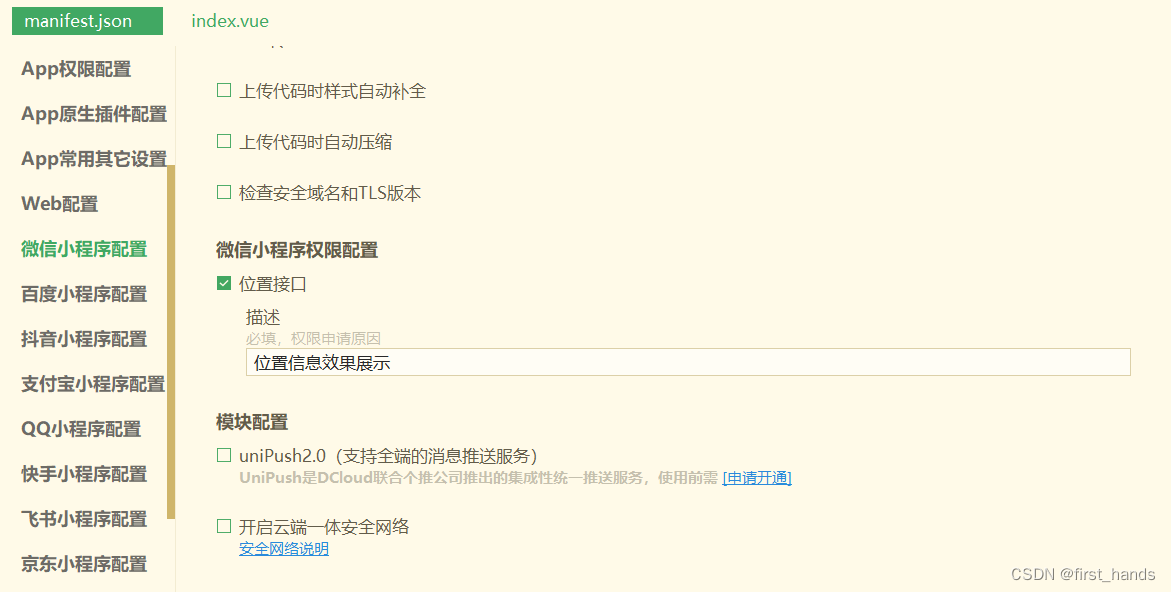
微信小程序地图应用总结版
1.应用场景:展示公司位置,并打开第三方app(高德,腾讯)导航到目标位置。 (1)展示位置地图 uniapp官网提供了相关组件,uniapp-map组件https://uniapp.dcloud.net.cn/component/map.ht…...
分支创建查看切换
1、初始化git目录,创建文件并将其推送到本地库 git init echo "123" > hello.txt git add hello.txt git commit -m "first commit" hello.txt$ git init Initialized empty Git repository in D:/Git/git-demo/.git/ AdministratorDESKT…...

参编三大金融国标,奇富科技以技术促行业规范化演进
近期,由中国互联网金融协会领导制定的《互联网金融智能风险防控技术要求》《互联网金融个人网络消费信贷信息披露》《互联网金融个人身份识别技术要求》三项国家标准颁布,由国家市场监督管理总局、国家标准化管理委员会发布,奇富科技作为核心…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...
