超图嵌入论文阅读2:超图神经网络
超图嵌入论文阅读2:超图神经网络
原文:Hypergraph Neural Networks ——AAAI2019(CCF-A)
源码:https://github.com/iMoonLab/HGNN 500+star
概述
贡献:用于数据表示学习的超图神经网络 (HGNN) 框架,对超图结构中的高阶数据相关性进行编码
-
定义超边卷积来处理表示学习过程中的数据相关性
-
够学习考虑高阶数据结构的隐藏层表示,是一个通用框架
——GCN可以看作是 HGNN 的一个特例,其中简单图中的边可以被视为仅连接两个顶点的 2 阶超边
-
引文图、图像识别数据集上实验,优于图卷积网络(GCN)
-
others:在处理多模态数据时具有优势
背景:
图卷积能够使用神经网络模型对不同输入数据的图结构进行编码,用于无监督、半监督、监督学习,在表示学习方面显示出优越性。传统图卷积网络,使用成对连接,难以表征多模态数据:
- 数据相关性可能比成对关系更复杂,很难用图结构建模
- 数据表示往往是多模态的
——传统的图结构具有规定数据相关性的局限性,这限制了图卷积网络的应用。
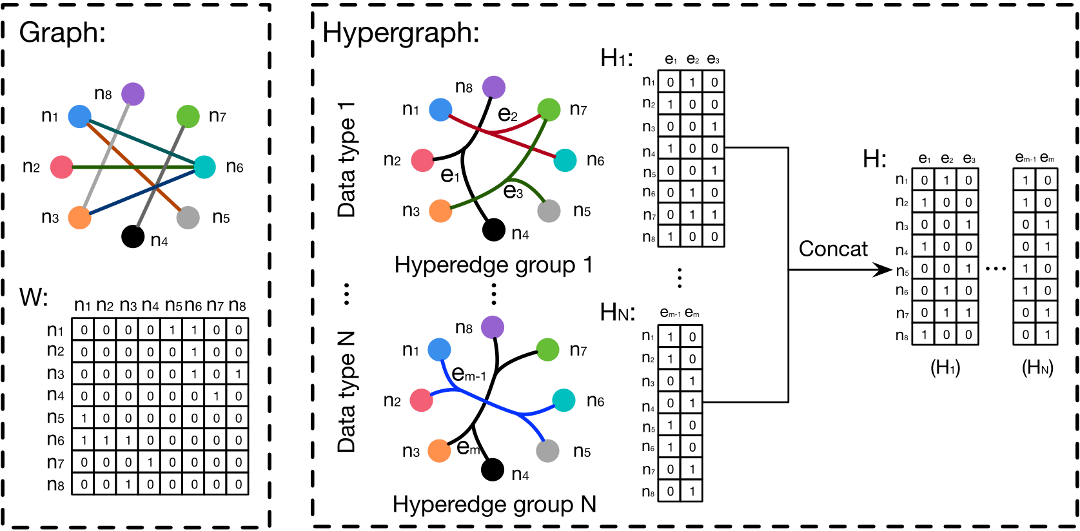
超图优势:
-
超图可以使用其可变度数超边对高阶数据相关性(超出成对连接)进行编码
-
使用超图的灵活性超边很容易扩展到多模态和异构数据表示:
如:可以通过组合邻接矩阵来联合使用多模态数据来生成超图
——图已被用于许多计算机视觉任务,例如分类和检索任务
超图问题:传统的超图学习方法计算复杂度和存储成本较高,难以广泛应用
相关研究:
-
超图学习
前期发展:
- 2007首次引入,转导推理旨在最小化超图上连接更强的顶点之间的标签差异
- 2009进一步用于视频对象分割
- 2010对图像关系进行建模,并进行转导推理过程进行图像排序
注意力机制引入:
- 2013对权重进行正则化
- 2008提出假设:高度相关的超边应该具有相似的权重
多模态:
- 2012引入多超图结构为不同的子超图分配权重
-
图神经网络
前期发展:
- 2005 2009应用循环神经网络来处理图
谱方法:
- 2014第一个图 CNN:图拉普拉斯特征基
- 2015谱滤波器可以使用平滑系数参数化
- 2016图拉普拉斯算子的切比雪夫扩展进一步用于近似谱滤波器
- 2017chebyshev 多项式被简化为 1 阶多项式,形成一个有效的逐层传播模型
空间方法:
- 2016使用转移矩阵的幂来定义节点的邻域
- 2017使用高斯混合模型形式的局部路径算子来概括空间域中的卷积
- 2018注意力机制被引入图以构建基于注意力的架构,以在图上执行节点分类任务
HGNN
超图学习
基础知识(略):
与简单图不同,超图中的超边连接两个或多个顶点。超图定义为 G = (V, E, W)
超图 G 可以用 |V| × |E|关联矩阵 H 表示
h ( v , e ) = { 1 , if v ∈ e 0 , if v ∉ e , h(v,e)=\left\{\begin{array}{l} 1, \text{if} \space v \in e \\ 0, \text{if} \space v \notin e, \\\end{array}\right. h(v,e)={1,if v∈e0,if v∈/e,
d ( v ) = ∑ e ∈ E ω ( e ) h ( v , e ) d(v) =∑_{e∈E} ω(e)h(v, e) d(v)=∑e∈Eω(e)h(v,e)、 δ ( e ) = ∑ v ∈ V h ( v , e ) δ(e) = ∑_{v∈V} h(v, e) δ(e)=∑v∈Vh(v,e)。 D e \mathbf{D}_e De 和 D v \mathbf{D}_v Dv 分别表示边度和顶点度的对角矩阵
超图节点分类问题:节点标签应该在超图结构上平滑
——用以下正则化框架描述:
arg min f { R e m p ( f ) + Ω ( f ) } \arg \min_f \{\mathcal{R}_{emp}(f)+\Omega(f)\} argfmin{Remp(f)+Ω(f)}
其中 Ω ( f ) \Omega(f) Ω(f) 是超图上的正则化, R e m p ( f ) \mathcal{R}_{emp}(f) Remp(f) 表示监督经验损失, f ( ⋅ ) f (·) f(⋅) 是分类函数。正则化 Ω ( f ) \Omega(f) Ω(f)定义为:
Ω ( f ) = 1 2 ∑ e ∈ ε ∑ { u , v } ∈ V w ( e ) h ( u , e ) h ( v , e ) δ ( e ) ( f ( u ) d ( u ) − f ( v ) d ( v ) ) 2 \Omega(f)=\frac{1}{2} \sum_{e \in \varepsilon} \sum_{\{u,v\}\in \mathcal{V}} \frac{w(e)h(u,e)h(v,e)}{\delta(e)} \left(\frac{f(u)}{\sqrt{d(u)}}-\frac{f(v)}{\sqrt{d(v)}}\right)^2 Ω(f)=21e∈ε∑{u,v}∈V∑δ(e)w(e)h(u,e)h(v,e)(d(u)f(u)−d(v)f(v))2
我们令 Θ = D v − 1 / 2 H W D e − 1 H T D v − 1 / 2 \mathbf \Theta=\mathbf D_v^{-1/2}\mathbf H \mathbf W \mathbf D_e^{-1}\mathbf H^{\mathsf T}\mathbf D_v^{-1/2} Θ=Dv−1/2HWDe−1HTDv−1/2, Δ = I − Θ \mathbf \Delta = \mathbf I -\mathbf \Theta Δ=I−Θ 归一化 Ω ( f ) \Omega(f) Ω(f) 可以写成:
Ω ( f ) = f T Δ \Omega(f)=f^{\text T} \mathbf \Delta Ω(f)=fTΔ
其中 Δ \mathbf \Delta Δ 是半正定的,通常称为超图拉普拉斯算子。
超图谱卷积
给定一个具有 n 个顶点的超图,拉普拉斯算子 Δ \mathbf \Delta Δ 是半正定的。对其进行特征分解 Δ = Φ Λ Φ T \mathbf \Delta =\mathbf \Phi \mathbf \Lambda \mathbf \Phi^{\mathsf T} Δ=ΦΛΦT 可得到正交特征向量 Φ = diag ( ϕ 1 , . . . , ϕ n ) \mathbf \Phi = \text{diag}(\phi_1,..., \phi_n) Φ=diag(ϕ1,...,ϕn) 和对角矩阵 Λ = diag ( λ 1 , . . . , λ n ) \mathbf \Lambda =\text{diag}(\lambda_1,..., \lambda_n) Λ=diag(λ1,...,λn) 对应非负特征值。
信号 x = ( x 1 , . . . , x n ) \text x = (x_1,..., x_n) x=(x1,...,xn) 在超图中定义为 x ^ = Φ T x \hat {\text x}=\mathbf \Phi^{\mathsf T}\text x x^=ΦTx ,其中特征向量被视为傅里叶基,特征值被解释为频率。信号x和滤波器g的谱卷积可以表示为:
g ⋆ x = Φ ( ( Φ T g ) ⊙ ( Φ T x ) ) = Φ g ( Λ ) Φ T x , \text g\star \text x=\mathbf \Phi((\mathbf \Phi^{\mathsf T}\text g)\odot (\mathbf \Phi^{\mathsf T} \text x))=\mathbf \Phi g(\mathbf \Lambda) \mathbf \Phi^{\mathsf T}\text x, g⋆x=Φ((ΦTg)⊙(ΦTx))=Φg(Λ)ΦTx,
- ⊙ \odot ⊙ 表示逐元素的Hadamard乘积
- g ( Λ ) = diag ( g ( λ 1 ) , . . . , g ( λ n ) ) g(\mathbf \Lambda)=\text{diag}(\text g(\lambda_1),...,\text g(\lambda_n)) g(Λ)=diag(g(λ1),...,g(λn)) 是傅立叶系数的函数
然而正向和反向傅里叶变换的计算成本为 O ( n 2 ) O(n^2) O(n2)。可以用某论文中的方法使用K 阶多项式参数化 g ( Λ ) g(\mathbf \Lambda) g(Λ),我们使用截断切比雪夫展开作为这样的多项式。Chebyshv多项式 T k ( x ) T_k(x) Tk(x)由 T k ( x ) = 2 x T k − 1 ( x ) − T k − 2 ( x ) T_k(x) = 2xT_{k−1}(x)−T_{k−2}(x) Tk(x)=2xTk−1(x)−Tk−2(x)递归计算,其中 T 0 ( x ) = 1 T_0(x) = 1 T0(x)=1和 T 1 ( x ) = x T_1(x) = x T1(x)=x。因此, g ( Λ ) g(\mathbf \Lambda) g(Λ)可以参数化为:
g ⋆ x ≈ ∑ k = 0 K θ k T k ( Δ ^ ) x , \text g\star \text x \approx \sum_{k=0}^K \theta_k T_k(\hat {\mathbf \Delta})\text{x}, g⋆x≈k=0∑KθkTk(Δ^)x,
其中 T k ( Δ ^ ) T_k(\hat {\mathbf \Delta}) Tk(Δ^) 是k阶切比雪夫多项式,里面的缩放拉普拉斯算子为 Δ ^ = 2 λ m a x Δ − I \hat{\mathbf \Delta}=\frac{2}{\lambda_{max}}\mathbf \Delta-\mathbf I Δ^=λmax2Δ−I。排除了拉普拉斯特征向量的扩展计算,只包括矩阵幂、加法和乘法,提升运算速度。我们可以进一步让 K = 1 来限制卷积操作的顺序,因为超图中的拉普拉斯算子已经可以很好地表示节点之间的高阶相关性。另一篇论文检建议,由于神经网络的规模适应性,令 λ m a x ≈ 2 \lambda_{max} \approx 2 λmax≈2,卷积运算可以进一步简化为:
g ⋆ x ≈ θ 0 x − θ 1 D v − 1 / 2 H W D e − 1 H T D v − 1 / 2 x , \text g\star \text x \approx \theta_0 \text x-\theta_1 \mathbf D_v^{-1/2}\mathbf H \mathbf W \mathbf D_e^{-1} \mathbf H^{\mathsf T} \mathbf D_v^{-1/2} \text x, g⋆x≈θ0x−θ1Dv−1/2HWDe−1HTDv−1/2x,
其中 θ 0 θ_0 θ0 和 θ 1 θ_1 θ1 是所有节点的过滤器参数。我们进一步使用单个参数 θ 来避免过拟合问题,定义为:
{ θ 1 = − 1 2 θ θ 0 = 1 2 θ D v − 1 / 2 H W D e − 1 H T D v − 1 / 2 , \left\{\begin{array}{l} \theta_1 = -\frac{1}{2}\theta \\ \theta_0 = \frac{1}{2}\theta \mathbf D_v^{-1/2}\mathbf H \mathbf W \mathbf D_e^{-1} \mathbf H^{\mathsf T} \mathbf D_v^{-1/2}, \\\end{array}\right. {θ1=−21θθ0=21θDv−1/2HWDe−1HTDv−1/2,
卷积运算可以简化为下式:
g ⋆ x ≈ 1 2 θ D v − 1 / 2 H ( W + I ) D e − 1 H T D v − 1 / 2 x ≈ θ D v − 1 / 2 H W D e − 1 H T D v − 1 / 2 x \text g\star \text x \approx \frac{1}{2}\theta \mathbf D_v^{-1/2}\mathbf H \mathbf {(W+I)} \mathbf D_e^{-1} \mathbf H^{\mathsf T} \mathbf D_v^{-1/2} \text x\\\approx \theta \mathbf D_v^{-1/2}\mathbf H \mathbf W \mathbf D_e^{-1} \mathbf H^{\mathsf T} \mathbf D_v^{-1/2} \text x g⋆x≈21θDv−1/2H(W+I)De−1HTDv−1/2x≈θDv−1/2HWDe−1HTDv−1/2x
其中 ( W + I ) \mathbf{(W + I)} (W+I) 可以看作是超边的权重。 W \mathbf W W 被初始化为单位矩阵,这意味着所有超边的相等权重。
当我们有一个具有n个节点和C1维特征的超图信号 X ∈ R n × C 1 \mathbf X \in \mathbb R^{n \times C_1} X∈Rn×C1 时,我们的超边卷积可以表示为:
Y = D v − 1 / 2 H W D e − 1 H T D v − 1 / 2 X Θ , \mathbf{Y=D_v^{-1/2}HWD_e^{-1}H^{\mathsf T}D_v^{-1/2}X\Theta}, Y=Dv−1/2HWDe−1HTDv−1/2XΘ,
其中 W = diag ( w 1 , . . . , w n ) \mathbf W =\text{diag}(\text{w}_1,...,\text{w}_n) W=diag(w1,...,wn), Θ ∈ R C 1 × C 2 \Theta \in \mathbb R^{C_1 \times C_2} Θ∈RC1×C2 是训练过程中要学习的参数。过滤器 Θ \mathbf \Theta Θ 应用于超图中的节点以提取特征。卷积后,我们可以得到 Y ∈ R n × C 2 \mathbf Y \in \mathbb R^{n \times C_2} Y∈Rn×C2 ,可用于分类。
超图神经网络分析
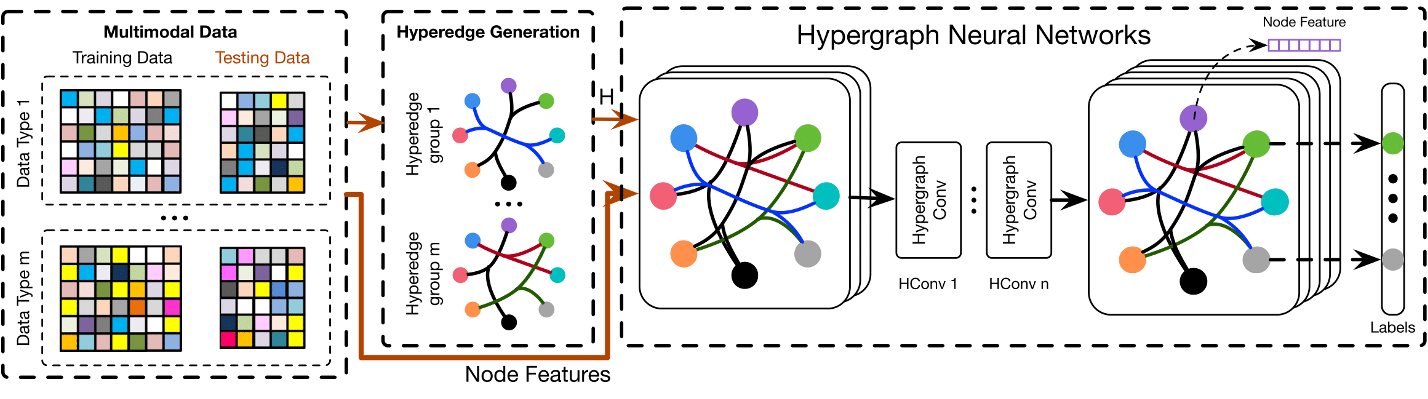
多模态数据集分为训练数据和测试数据,每个数据包含多个具有特征的节点。然后从多模态数据集的复杂相关性构建多个超边结构组。我们组合超边组以生成超图邻接矩阵 H \mathbf H H。将超图邻接矩阵 H \mathbf H H和节点特征输入到HGNN中,得到节点输出标签。
我们可以在以下公式中构建一个超边卷积层 f ( X , W , Θ ) f \mathbf{(X, W, \Theta)} f(X,W,Θ):
X ( l + 1 ) = σ ( D v − 1 / 2 H W D e − 1 H T D v − 1 / 2 X ( l ) Θ ( l ) ) , \mathbf X^{(l+1)}=\sigma (\mathbf D_v^{-1/2}\mathbf H \mathbf W \mathbf D_e^{-1} \mathbf H^{\mathsf T} \mathbf D_v^{-1/2} \mathbf X^{(l)} \mathbf \Theta^{(l)}), X(l+1)=σ(Dv−1/2HWDe−1HTDv−1/2X(l)Θ(l)),
其中 X ( l ) ∈ R N × C \mathbf X^{(l)} \in \mathbb R^{N \times C} X(l)∈RN×C 是 l l l 层的超图信号, X ( 0 ) = X \mathbf X^{(0)} = \mathbf X X(0)=X, σ \sigma σ 表示非线性激活函数。
卷积层结构:
HGNN模型基于超图上的谱卷积。HGNN 层可以执行 节点-边-节点 的变换,这可以有效地提取超图上的高阶相关性。
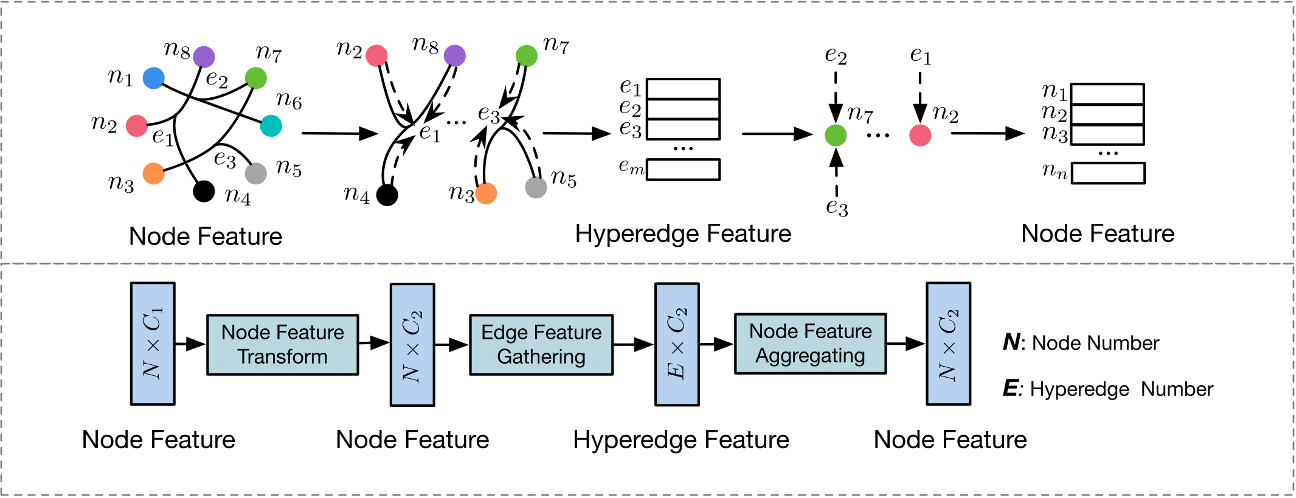
- 初始节点特征 X ( 1 ) \mathbf X^{(1)} X(1) 由可学习的滤波器矩阵 Θ ( 1 ) \mathbf \Theta^{(1)} Θ(1) 处理以提取 C 2 C_2 C2- 维特征
- 据超边收集节点特征以形成超边特征 R E × C 2 \mathbb R^{E \times C_2} RE×C2 ,这是通过乘以矩阵 H T ∈ R E × N \mathbf {H^{\mathsf T}} \in \mathbb R^{\mathbf {E \times N}} HT∈RE×N 来实现的
- 通过聚合其相关的超边特征来获得输出节点特征,该特征是通过乘以矩阵 H \mathbf H H 来实现的
—— D v \mathbf D_v Dv和 D e \mathbf D_e De在公式11中起到了归一化的作用
与现有方法的关系:
超边只连接两个顶点时,超图被简化为一个简单的图,拉普拉斯算子 Δ \mathbf \Delta Δ 也与简单图的拉普拉斯算子一致(1/2倍相乘)
- HGNN可以自然地对数据之间的高阶关系进行建模,有效地利用和编码形成特征提取
- 与传统的超图方法相比,我们的模型在计算上非常高效,没有拉普拉斯算子 Δ \mathbf \Delta Δ 的逆运算
- 在超边生成的灵活性下对多模态特征具有很大的可扩展性
实施
- 超图构造:图片分类任务中,提取每个对象的特征,根据欧氏距离构建超图。每个顶点代表一个视觉对象,每个超边通过连接一个顶点及其 K 个最近邻居来形成,这带来了 N 个链接 K + 1 个顶点的超边。引文图也类似地构造。
- 节点分类模型:数据集分为训练数据和测试数据,构建超图。按上图搭建网络,构建了一个两层HGNN模型,使用softmax 函数生成预测标签。使用交叉熵损失函数,将各种超边融合在一起,对数据的复杂关系进行建模。
实验
两个任务:引文网络分类和视觉对象识别,与图卷积网络和其他最先进的方法进行比较。
引文网络分类
Cora 和 Pubmed两个数据集:
- 每个数据的特征是文档的词袋表示
- 每次选择图中的每个顶点作为质心,其连通顶点用于生成一条超边,包括质心本身
- 获得与原始图规模相同的关联矩阵
- Cora2708 个5%标记,Pubmed19717 个0.3%标记
参数设置:两层 HGNN
- 隐藏层的特征维度设置为 16
- dropout 丢弃率 p = 0.5
- ReLU 作为非线性激活函数
- Adam 优化器最小化交叉熵损失函数
- 学习率为 0.001
结果讨论:Core和Pumbed上100次运行的平均分类精度
-
与最先进的方法相比,HGNN模型可以达到最佳或相当的性能
——与 GCN 相比,HGNN 方法在 Cora 数据集上略有改进,在 Pubmed 数据集上提高了 1.1%
-
HGNN 获得的增益并不是很显著——因为构建的超图和传统图差不多
视觉对象分类
数据集:
- 普林斯顿ModelNet40
- 国立台湾大学(NTU) 3D模型数据集
超图构建:
-
特征使用多视图卷积神经网络 (MVCNN) 和组视图卷积神经网络 (GVCNN)提取
-
根据节点的距离构造一个概率图,生成亲和矩阵A来表示不同顶点之间的关系
A i j = exp ( − 2 D i j 2 Δ ) A_{ij}=\exp(-\frac{2D_{ij}^2}{\Delta}) Aij=exp(−Δ2Dij2)
其中Dij表示节点i和节点j之间的欧氏距离。Δ 是节点之间的平均成对距离
-
两种超图构建方法:
- 基于单模态特征:每次选择一个数据集中的一个对象作为质心,选取特征空间中的10个最近邻生成一个超边,包括质心本身
- 基于多模态特征:使用多个特征来生成建模复杂多模态相关性的超图 G,只需要将超图关联矩阵拼接即可
结果讨论:
- HGNN方法在ModelNet40数据集中优于最先进的目标识别方法:分别获得 4.8% 和 3.2% 的增益
- 与 GCN 相比,所提出的方法在所有实验中都取得了更好的性能:一个特征取得轻微改进,多个特征改进明显
优势分析
- 超图结构能够传达数据之间的复杂关系和高阶相关性,与图结构或没有图结构的方法相比,可以更好地表示底层的数据关系。
- 当多模态数据/特征可用时,HGNN 的优势在于通过其灵活的超边将这种多模态信息组合在同一结构中。
- 与传统的超图学习方法可能存在计算复杂度高、存储成本高的问题相比,所提出的HGNN框架通过超边卷积运算效率更高。
结论
超图神经网络 (HGNN) 的框架
- 将卷积运算推广到超图学习过程:谱域的卷积用超图拉普拉斯算子进行,进一步用截断的切比雪夫多项式逼近
- 是一个更通用的框架:与传统图相比,能够通过超图结构处理复杂和高阶相关性以进行表示学习
- 对引文网络分类和视觉对象识别任务进行了实验:HGNN 模型有更好的性能
——HGNN能够将复杂的数据相关性纳入表示学习,从而在视觉识别、检索和数据分类等许多任务中带来潜在的广泛应用。
相关文章:

超图嵌入论文阅读2:超图神经网络
超图嵌入论文阅读2:超图神经网络 原文:Hypergraph Neural Networks ——AAAI2019(CCF-A) 源码:https://github.com/iMoonLab/HGNN 500star 概述 贡献:用于数据表示学习的超图神经网络 (HGNN) 框架…...
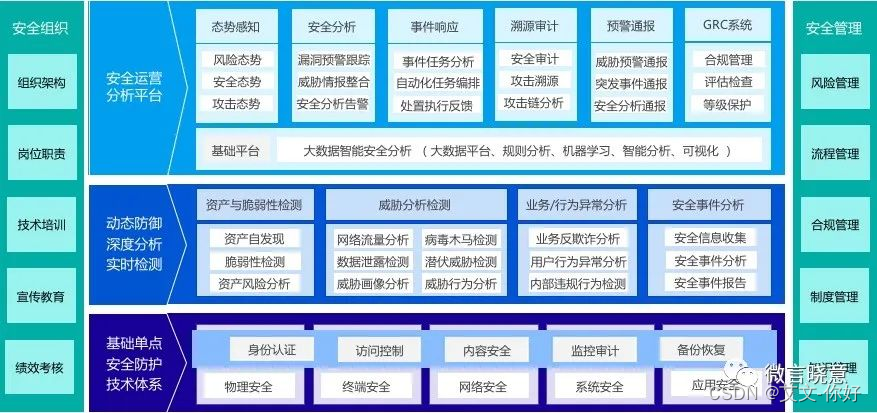
安全运营中心(SOC)技术框架
2018年曾经画过一个安全运营体系框架,基本思路是在基础单点技术防护体系基础上,围绕着动态防御、深度分析、实时检测,建立安全运营大数据分析平台,可以算作是解决方案产品的思路。 依据这个体系框架,当时写了《基于主动…...
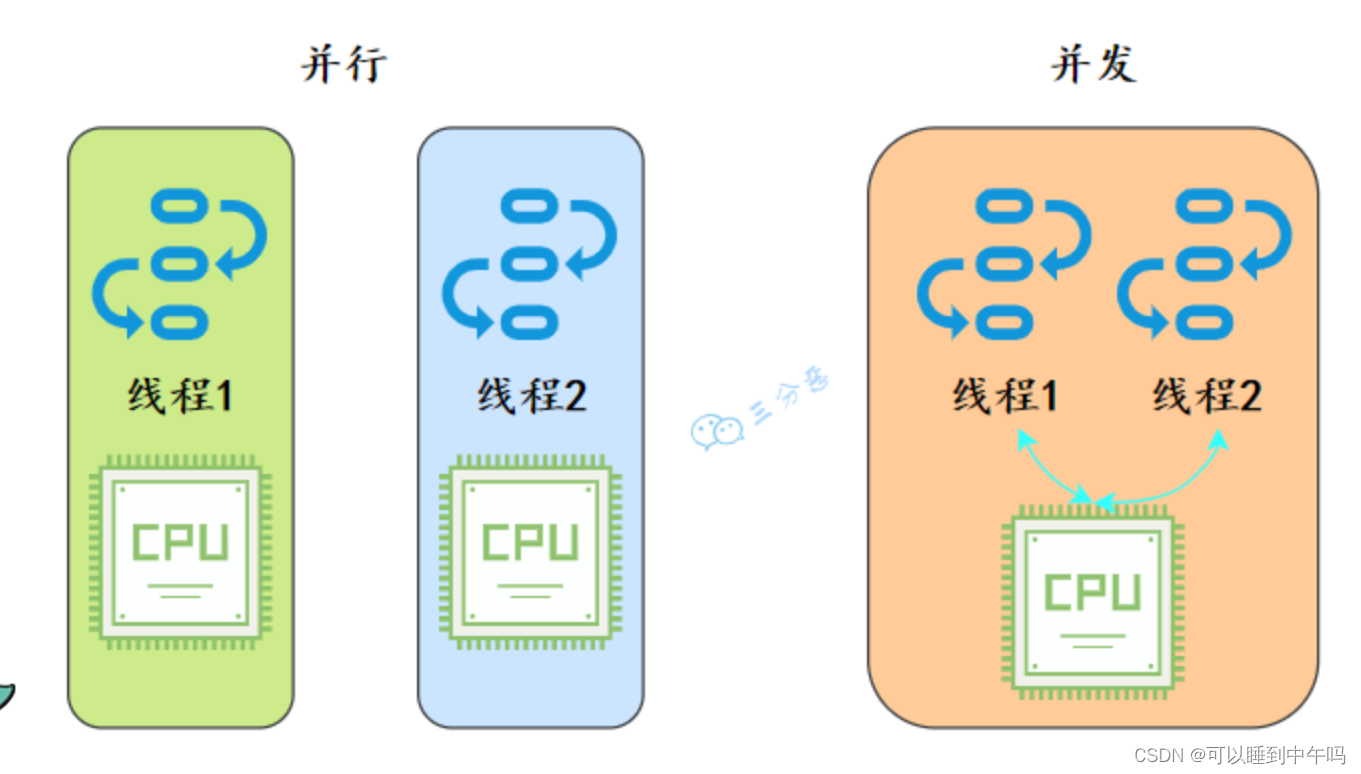
并行和并发的区别
从操作系统的角度来看,线程是CPU分配的最小单位。 并行就是同一时刻,两个线程都在执行。这就要求有两个CPU去分别执行两个线程。并发就是同一时刻,只有一个执行,但是一个时间段内,两个线程都执行了。并发的实现依赖于…...
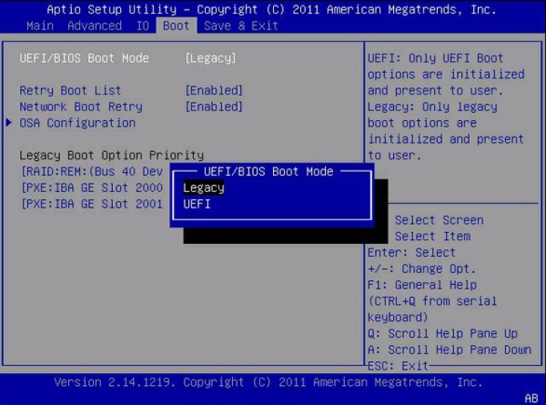
GPT转换工具:轻松将MBR转换为GPT磁盘
为什么需要将MBR转换为GPT? 众所周知,Windows 11已经发布很长时间了。在此期间,许多老用户已经从Windows 10升级到Windows 11。但有些用户仍在运行Windows 10。对于那些想要升级到Win 11的用户来说,他们可能不确定Win 11应该使…...
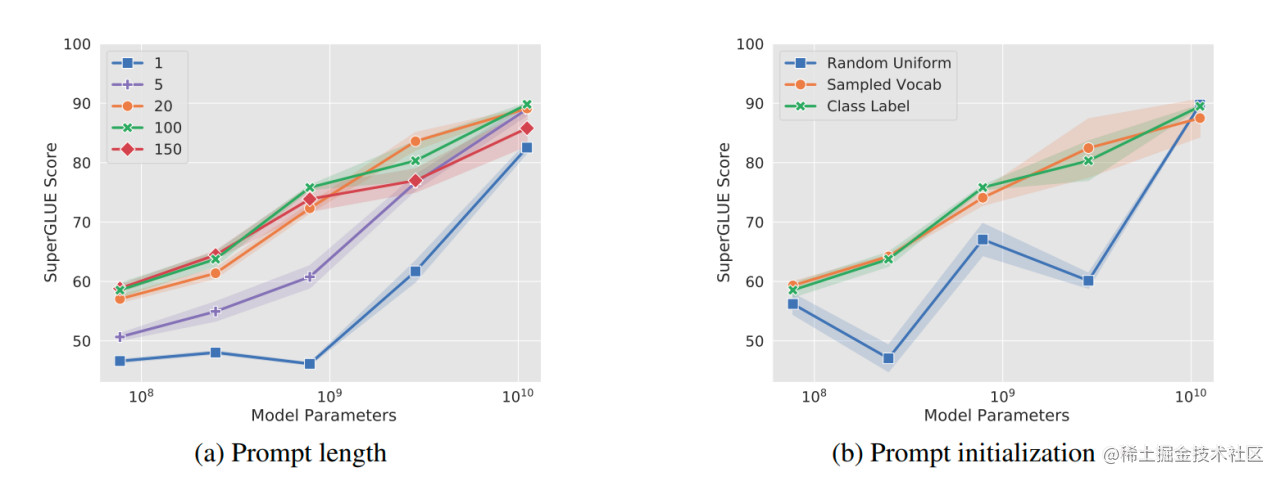
大模型参数高效微调技术原理综述(二)-BitFit、Prefix Tuning、Prompt Tuning
随着,ChatGPT 迅速爆火,引发了大模型的时代变革。然而对于普通大众来说,进行大模型的预训练或者全量微调遥不可及。由此,催生了各种参数高效微调技术,让科研人员或者普通开发者有机会尝试微调大模型。 因此,…...

将conda环境打包成docker步骤
1. 第一步,将conda环境的配置导出到environment.yml 要获取一个Conda环境的配置文件 environment.yml,你可以使用以下命令从已存在的环境中导出: conda env export --name your_env_name > environment.yml请将 your_env_name 替换为你要…...

C# 获取Json对象中指定属性的值
在C#中获取JSON对象中指定属性的值,可以使用Newtonsoft.JSON库的JObject类 using Newtonsoft.Json.Linq; using System; public class Program { public static void Main(string[] args) { string json "{ Name: John, age: 30, City: New York }"; …...
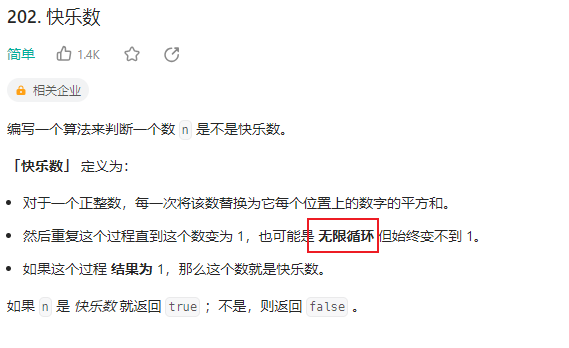
【LeetCode】202. 快乐数 - hash表 / 快慢指针
目录 2023-9-5 09:56:152023-9-6 19:40:51 202. 快乐数 2023-9-5 09:56:15 关键是怎么去判断循环: hash表: 每次生成链中的下一个数字时,我们都会检查它是否已经在哈希集合中。 如果它不在哈希集合中,我们应该添加它。如果它在…...

什么是多态性?如何在面向对象编程中实现多态性?
1、什么是多态性?如何在面向对象编程中实现多态性? 多态性(Polymorphism)是指在同一个方法调用中,由于参数类型不同,而产生不同的行为。在面向对象编程中,多态性是一种重要的特性,它…...
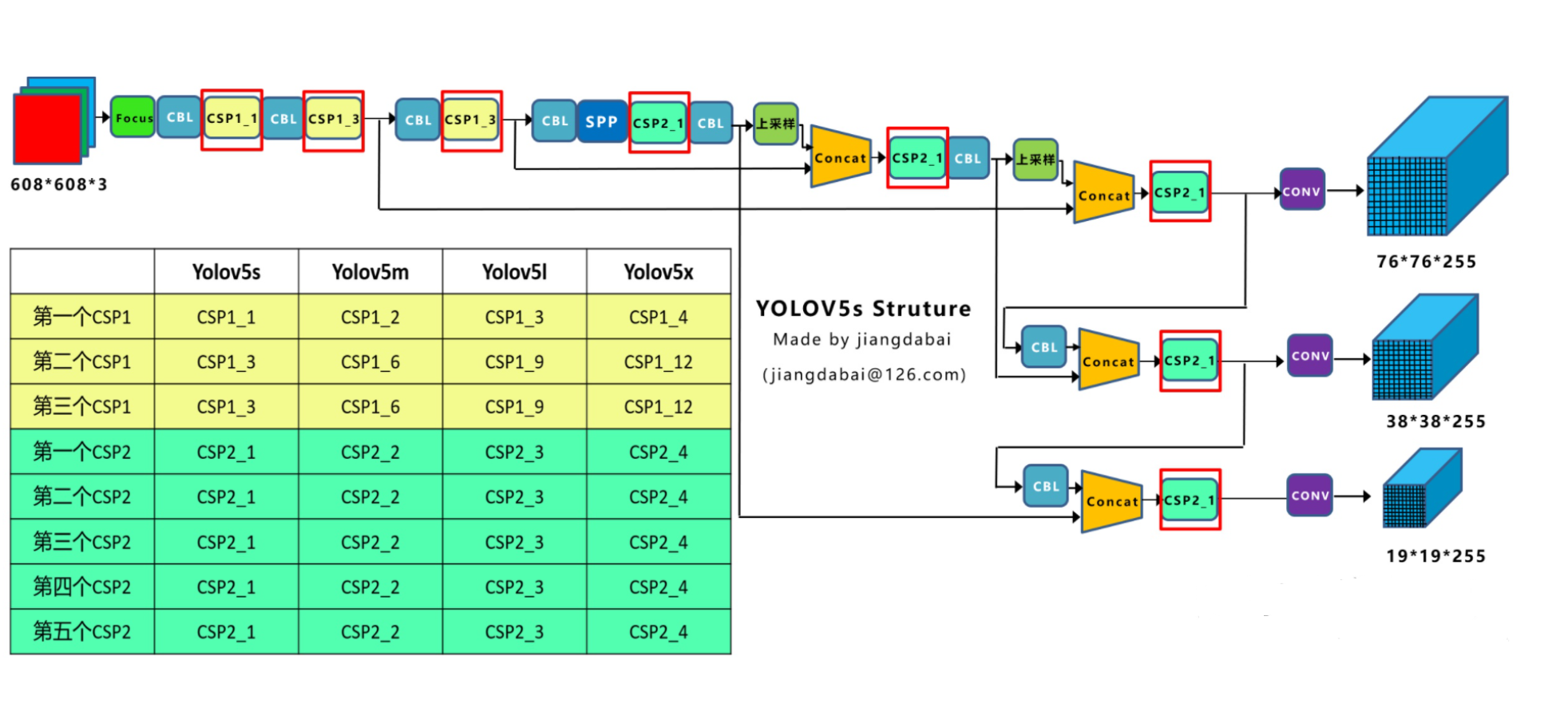
【目标检测】理论篇(3)YOLOv5实现
Yolov5网络构架实现 import torch import torch.nn as nnclass SiLU(nn.Module):staticmethoddef forward(x):return x * torch.sigmoid(x)def autopad(k, pNone):if p is None:p k // 2 if isinstance(k, int) else [x // 2 for x in k] return pclass Focus(nn.Module):def …...
IDEA爪哇操作数据库
少小离家老大回,乡音无改鬓毛衰 ⒈.IDEA2018设置使用主题颜色 IDEA2018主题颜色分为三种:idea原始颜色,高亮色,黑色 设置方法:Settings–Appearance&Behavior–Appearance ⒉.mysql中,没有my.ini,只有…...
一文速学-让神经网络不再神秘,一天速学神经网络基础(七)-基于误差的反向传播
前言 思索了很久到底要不要出深度学习内容,毕竟在数学建模专栏里边的机器学习内容还有一大半算法没有更新,很多坑都没有填满,而且现在深度学习的文章和学习课程都十分的多,我考虑了很久决定还是得出神经网络系列文章,…...

C++ 异常处理——学习记录007
1. 概念 程序中的错误分为编译时错误和运行时错误。编译时出现的错误包括关键字拼写出错、语句分号缺少、括号不匹配等,编译时的错误容易解决。运行时出现的错误包括无法打开文件、数组越界和无法实现指定的操作。运行时出现的错误称为异常,对异常的处理…...

【BIM+GIS】“BIM+”是什么? “BIM+”技术详解
对于我们日常生活影响最大的是信息化和网络化给我们的日常生活带来革命性的变化。“互联网+“在建筑行业里可以称为“BIM+”。“BIM+”"即是通过BIM与各类技术(互联网、大数据等)结合去完成不同的任务。将产品的全生命周期和全制造流程的数字化以及基于信息通信技术的模块…...

Flink算子如何限流
目录 使用方法 调用类图 内部源码 GuavaFlinkConnectorRateLimiter RateLimiter 使用方法 重写AbstractRichFunction中的open()方法,在处理数据前调用limiter.acquire(1); 调用limiter.open(getRuntimeContext())的源码,实际内部是RateLimiter,根据并行度算出subTask…...

垃圾分代收集的过程是怎样的?
垃圾分代收集是Java虚拟机(JVM)中一种常用的垃圾回收策略。该策略将堆内存分为不同的代(Generation),通常分为年轻代(Young Generation)和老年代(Old Generation)。不同代的对象具有不同的生命周期和回收频率。 下面是Java中垃圾分代收集的一般过程: 1…...
NPM 常用命令(四)
目录 1、npm diff 1.1 描述 1.2 过滤文件 1.3 配置 diff diff-name-only diff-unified diff-ignore-all-space diff-no-prefix diff-src-prefix diff-dst-prefix diff-text global tag workspace workspaces include-workspace-root 2、npm dist-tag 2.1 常…...
Anaconda虚拟环境下导入opencv
文章目录 解决方法测试 解决方法 1、根据自己虚拟环境对于的python版本与电脑对应的位长选择具体的版本,例如python3.9选择cp39,64位电脑选择64 下载地址:资源地址 若是不确定自己虚拟环境对应的python版本,可以输入下列命令&…...
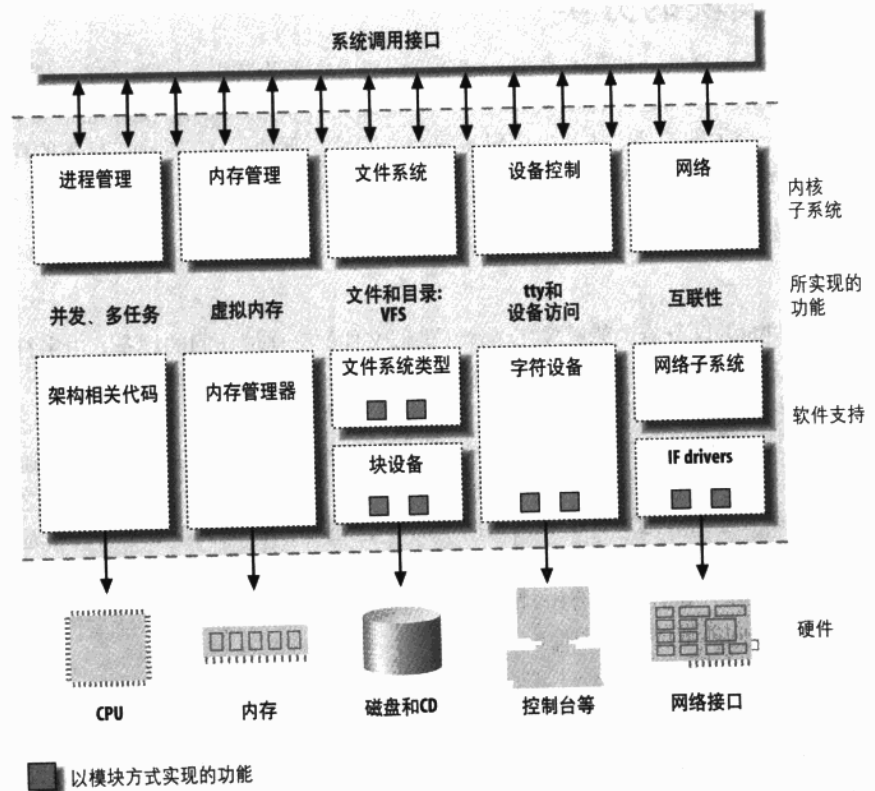
Linux设备驱动程序
一、设备驱动程序简介 图1.1 内核功能的划分 可装载模块 Linux有一个很好的特性:内核提供的特性可在运行时进行扩展。这意味着当系统启动 并运行时,我们可以向内核添加功能( 当然也可以移除功能)。 可在运行时添加到内核中的代码被称为“模块”。Linux内核支持好几…...

mybatis <if>标签判断“0“不生效
原if标签写法 <if test"type 0"><!--内部逻辑--> </if> 这种情况不生效,原因是mybatis是用OGNL表达式来解析的,在OGNL的表达式中,0’会被解析成字符(而我传入的type却是string),java是强类型的,cha…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...
