(数字图像处理MATLAB+Python)第十一章图像描述与分析-第五、六节:边界描述和矩描述
文章目录
- 一:边界描述
- (1)边界链码
- A:概述
- B:边界链码改进
- C:程序
- (2)傅里叶描绘子
- A:概述
- B:程序
- 二:矩描述
- (1)矩
- A:几何矩
- B:不变矩组
- (2)与矩相关的特征
- A:二阶矩
- B:主轴
- C:等效椭圆
- D:偏心率
一:边界描述
(1)边界链码
A:概述
边界链码:是一种用于图像处理和计算机视觉领域的技术,主要用于描述二进制图像中物体的轮廓。边界链码通过将轮廓转化为一系列有序的连续像素点来表示。边界链码的基本思想是从图像中选择一个起始点,然后按照一定的顺序遍历相邻像素,将它们连接起来形成一个闭合的轮廓。这些相邻像素的连接方式可以根据具体的算法不同而有所差异,常见的有4邻域链码和8邻域链码

如下图,以左下角0点为起始点,设其坐标为(0,3),4方向和8方向链码表示区域边界,则
- 4方向链码:(0,3)0 0 0 1 1 1 2 3 2 3 2 3
- 8方向链码:(0,3)0 0 0 2 2 2 4 5 5 6
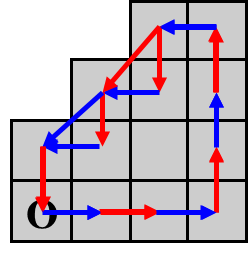
边界链码特点如下
- 由于表示一个方向数比表示一个坐标值所需比特数少,而且对每一个点又只需一个方向数就可以代替两个坐标值,因此链码表达可大大减少边界表示所需的数据量
- 可以很方便地获取相关几何特征,如区域的周长
- 隐含了区域边界的形状信息
边界链码缺点如下
- 码串比较长
- 噪声等干扰会导致小的边界变化,从而使链码发生与目标整体形状无关的较大变动
- 目标平移时,链码不变,但目标旋转时,链码会发生变化
B:边界链码改进
多重网格采样:对原边界以较大的网格重新采样,并把与原边界点最接近的大网格点定为新的边界点。也可用于消除目标尺度变化链码的影响
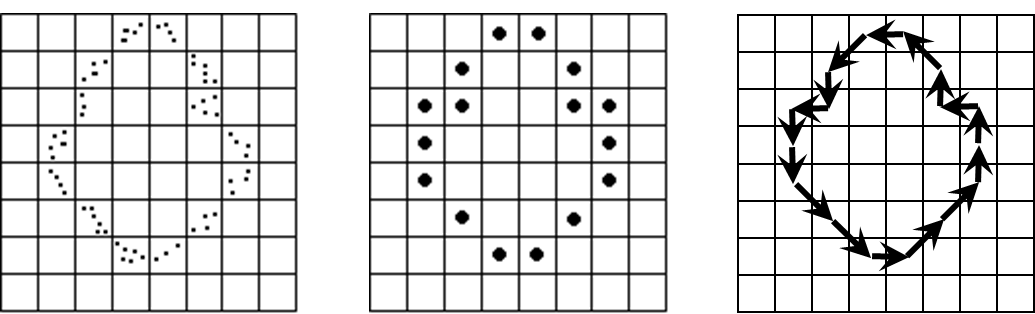
边界链码的起点:起点不同,链码不同。把链码归一化可解决这个问题
- 给定一个从任意点开始产生的链码,把它看作一个由各方向数构成的自然数
- 将这些方向数依一个方向循环,以使它们所构成的自然数的值最小;
- 将转换后所对应的链码起点作为这个边界的归一化链码的起点
一阶差分链码:链码中相邻两个方向数按反方向相减(后一个减前一个),目标发生旋转时,一阶差分链码不发生变化
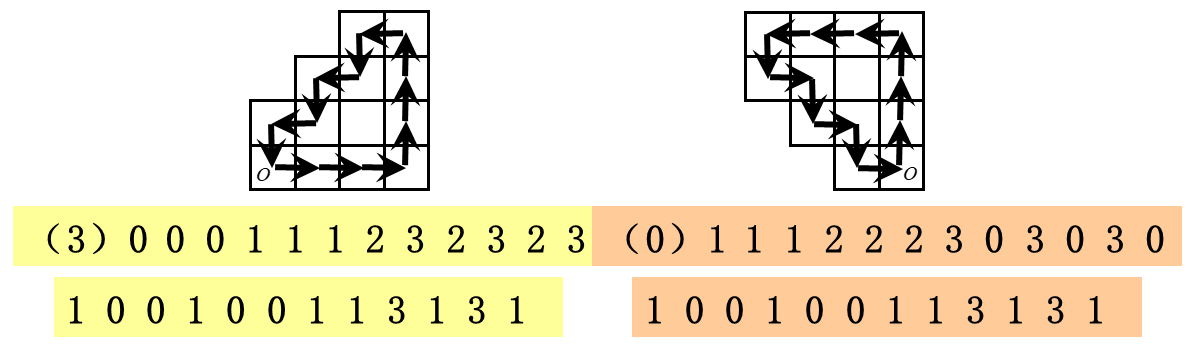
C:程序
如下,统计边界链码,并利用链码重构目标区域边界

matlab:
clear,clc,close all;
image=imread('morphplane.jpg');
figure,imshow(image),title('Ôͼ');
BW=im2bw(image);
[B,L]=bwboundaries(1-BW);
len=length(B);
chain=cell(len,1);
startpoint=zeros(len,2);
for i=1:lenboundary=B{i};everylen=length(boundary);startpoint(i,:)=boundary(1,:);for j=1:everylen-1candidate=[0 1;-1 1;-1 0;-1 -1;0 -1;1 -1;1 0;1 1];y=boundary(j+1,1)-boundary(j,1);x=boundary(j+1,2)-boundary(j,2); [is,pos]=ismember([y x],candidate,'rows'); chain{i}(j)=pos-1; end
end
figure,imshow(L),title('»æÖÆÁ´Âë');
hold on
for i=1:lenx=startpoint(i,2);y=startpoint(i,1);plot(x,y,'r*','MarkerSize',12);boundary=chain{i};everylen=length(boundary);for j=1:everylencandidate=[y x+1;y-1 x+1;y-1 x;y-1 x-1;y x-1;y+1 x-1;y+1 x;y+1 x+1];next=candidate(boundary(j)+1,:);x=next(2);y=next(1);plot(x,y,'g.');end
endpython:
import numpy as np
import matplotlib.pyplot as plt
from skimage import io, color, measure# 读取图像
image = io.imread('morphplane.jpg')
plt.imshow(image)
plt.title('原始图片')
plt.show()# 图像二值化处理
bw = color.rgb2gray(image) > 0.5# 提取边界
boundaries = measure.find_boundaries(1 - bw)# 获取边界链码
chain = []
startpoints = []for boundary in measure.find_contours(boundaries, 0.5):startpoint = boundary[0].astype(int)startpoints.append(startpoint)chain_segment = []for i in range(len(boundary)-1):y = boundary[i+1, 0] - boundary[i, 0]x = boundary[i+1, 1] - boundary[i, 1]candidate = np.array([[0, 1], [-1, 1], [-1, 0], [-1, -1], [0, -1], [1, -1], [1, 0], [1, 1]])pos = np.where((candidate == [y, x]).all(axis=1))[0][0]chain_segment.append(pos)chain.append(chain_segment)# 显示边界链码
fig, ax = plt.subplots()
ax.imshow(boundaries)
ax.set_title('边界链码')
for i in range(len(startpoints)):startpoint = startpoints[i]ax.plot(startpoint[1], startpoint[0], 'r*', markersize=12)boundary = chain[i]y, x = startpointfor j in range(len(boundary)):candidate = np.array([[y, x+1], [y-1, x+1], [y-1, x], [y-1, x-1], [y, x-1], [y+1, x-1], [y+1, x], [y+1, x+1]])next_point = candidate[boundary[j]]x, y = next_pointax.plot(x, y, 'g.')plt.show()(2)傅里叶描绘子
A:概述
傅里叶描绘子:是一种常用于形状描述和图像处理的数学方法。它利用傅里叶变换的思想,将一个封闭曲线或轮廓分解为一系列频谱成分,从而对形状进行表示和比较。傅里叶描绘子的基本原理是将曲线表示为一系列复数,每个复数代表了曲线上的一个点。通过对这些复数进行傅里叶变换,可以得到频谱信息。在傅里叶变换中,高频成分表示了曲线的细节和局部特征,低频成分表示了曲线的整体形状。其计算步骤如下
- 对封闭曲线或轮廓进行采样,获取一系列坐标点
- 将坐标点转换为复数形式,即将每个点的 x x x和 y y y坐标看作是实部和虚部构成的复数
- 对复数序列进行离散傅里叶变换(DFT),得到频域表示
- 根据需要选择保留的频率成分,可以通过截断高频成分来降低数据量或者提取感兴趣的特征
- 对保留的频率成分进行逆傅里叶变换(IDFT),得到原始坐标点的复数表示
- 将复数表示转换为实部和虚部,得到重建后的坐标点
通过傅里叶描绘子,可以对形状进行压缩、匹配和比较。由于傅里叶变换具有平移、旋转和尺度不变性,因此傅里叶描绘子也具有这些不变性,使得它在形状识别、目标跟踪和图像检索等领域有广泛应用
B:程序
如下,分割图像,计算各区域边界点的傅里叶描绘子并重建边界
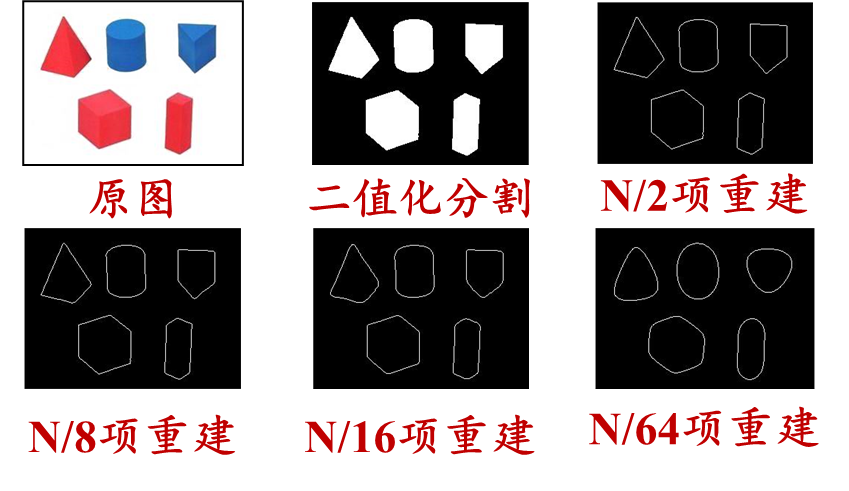
matlab:
Image=rgb2gray(imread('bricks.jpg'));
figure,imshow(Image),title('原始图像');
T=graythresh(Image); %获取阈值T
result=im2bw(Image,T); %二值化图像
S=zeros(size(Image));
[B,L]=bwboundaries(1-result);
for k=1:length(B) N=length(B{k});if N/2~=round(N/2)B{k}(end+1,:)=B{k}(end,:);N=N+1;endz=B{k}(:,2)+1i*B{k}(:,1); for m=[N/2 N*24/32 N*60/64 N*126/128]Z=fft(z);[Y,I]=sort(abs(Z));for count=1:mZ(I(count))=0;endzz=ifft(Z);figure,imshow(S);hold on;plot(real(zz),imag(zz),'w');end
endpython:
import numpy as np
import matplotlib.pyplot as plt
from skimage import io, color, filters# 读取图像并转为灰度图像
image = color.rgb2gray(io.imread('bricks.jpg'))
plt.imshow(image, cmap='gray')
plt.title('原始图像')
plt.show()# 二值化图像
threshold = filters.threshold_otsu(image)
result = image > threshold# 初始化画布
S = np.zeros_like(image)# 获取边界
boundaries = color.label2rgb(result, image, kind='overlay')
contours = measure.find_contours(result, 0.5)# 绘制傅里叶描绘子
for contour in contours:N = len(contour)if N % 2 != 0:contour = np.append(contour, [contour[-1]], axis=0)N += 1z = contour[:, 1] + 1j * contour[:, 0]for m in [N/2, N*24/32, N*60/64, N*126/128]:Z = np.fft.fft(z)I = np.argsort(np.abs(Z))for count in range(int(m)):Z[I[count]] = 0zz = np.fft.ifft(Z)plt.imshow(S, cmap='gray')plt.hold(True)plt.plot(np.real(zz), np.imag(zz), 'w')plt.show()二:矩描述
(1)矩
A:几何矩
几何矩:是一种用于描述图像或形状的数学特征。它们通过对图像或形状的像素值及其位置进行加权求和来计算,提供了关于形状的位置、大小、方向以及形态特征的信息。几何矩的计算基于图像或形状的二维坐标系,并使用不同的权重函数来表示不同的特征
- 一阶几何矩:是形状的质心(centroid),它表示形状的位置信息
- 二阶几何矩:包括中心距(central moments),可以获得形状的尺寸和形态特征,例如面积、面积矩、最大、最小轴长和方向等
- 三阶几何矩和高阶几何矩:提供了更丰富的形态信息,如形状的对称性、弯曲程度等
几何矩计算公式如下
- 零阶几何矩(面积): M 00 = ∑ ∑ I ( x , y ) M_{00} = \sum \sum I(x, y) M00=∑∑I(x,y)
- 一阶几何矩(质心): M 10 = ∑ ∑ x ⋅ I ( x , y ) , M 01 = ∑ ∑ y ⋅ I ( x , y ) M_{10} = \sum \sum x \cdot I(x, y), \quad M_{01} = \sum \sum y \cdot I(x, y) M10=∑∑x⋅I(x,y),M01=∑∑y⋅I(x,y)
- 二阶几何矩(中心矩): μ 20 = ∑ ∑ ( x − x c ) 2 ⋅ I ( x , y ) , μ 02 = ∑ ∑ ( y − y c ) 2 ⋅ I ( x , y ) , μ 11 = ∑ ∑ ( x − x c ) ( y − y c ) ⋅ I ( x , y ) \mu_{20} = \sum \sum (x - x_c)^2 \cdot I(x, y), \quad \mu_{02} = \sum \sum (y - y_c)^2 \cdot I(x, y), \quad \mu_{11} = \sum \sum (x - x_c)(y - y_c) \cdot I(x, y) μ20=∑∑(x−xc)2⋅I(x,y),μ02=∑∑(y−yc)2⋅I(x,y),μ11=∑∑(x−xc)(y−yc)⋅I(x,y)
B:不变矩组
不变矩组:是一种用于图像处理和模式识别的特征描述方法。它基于几何矩的概念,通过对图像或形状的几何矩进行归一化和旋转不变性的处理,生成一组具有唯一性和稳定性的特征向量,用于表示和比较图像或形状。计算步骤如下
- 将图像或形状转换为灰度图像,并对其进行二值化处理
- 计算二值化图像的几何矩,包括零阶、一阶和二阶矩
- 根据几何矩计算归一化中心矩,将几何矩除以零阶矩的幂次来消除尺度的影响
- 根据归一化中心矩计算不变矩,通过对几何矩进行线性组合和归一化得到一组不变矩
- 对不变矩进行平移、旋转和缩放等操作,使其具有平移和旋转不变性
(2)与矩相关的特征
A:二阶矩
二阶矩:也称为方差(Variance),是统计学中常用的描述数据分布离散程度的指标。在图像处理和模式识别中,二阶矩被广泛应用于描述图像的纹理特征和灰度分布特性。对于一维数据集,二阶矩定义为每个数据点与数据集均值之差的平方的平均值。对于二维数据集或图像,二阶矩是对数据点与数据集均值之差的平方的期望
{ M 20 = ∑ x = 0 M − 1 ∑ y = 0 N − 1 x 2 f ( x , y ) M 02 = ∑ x = 0 M − 1 ∑ y = 0 N − 1 y 2 f ( x , y ) \left\{\begin{array}{l}M_{20}=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1} x^{2} f(x, y) \\M_{02}=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1} y^{2} f(x, y)\end{array}\right. {M20=∑x=0M−1∑y=0N−1x2f(x,y)M02=∑x=0M−1∑y=0N−1y2f(x,y)
B:主轴
主轴:是指图形、形状或区域的特征轴线,它描述了形状的主要方向和旋转情况。主轴通常使用惯性矩阵来计算,通过分析图像或形状在不同方向上的质量分布来确定主轴的方向和长度
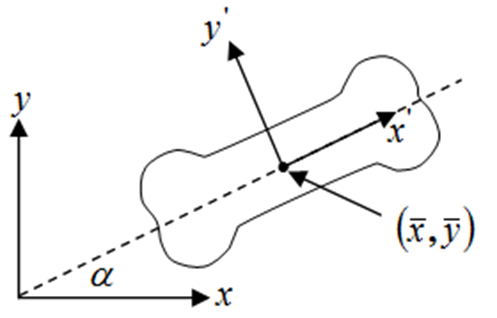
C:等效椭圆
等效椭圆:是用于描述图形或形状的一种几何模型,它能够近似地表示原始图形的外形和尺寸。等效椭圆通常是通过对图形的边界进行拟合得到的,使得椭圆与图形的形状最相似
{ a = [ 2 ( μ 20 + μ 02 + ( μ 20 − μ 02 ) 2 + 4 μ 11 2 ) 1 2 μ 00 ] 1 2 ] 1 2 b = [ 2 ( μ 20 + μ 02 − ( μ 20 − μ 02 ) 2 + 4 μ 11 2 μ 00 ] 1 2 \left\{\begin{array}{l}\left.a=\left[\frac{2\left(\mu_{20}+\mu_{02}+\sqrt{\left(\mu_{20}-\mu_{02}\right)^{2}+4 \mu_{11}^{2}}\right)^{\frac{1}{2}}}{\mu_{00}}\right]^{\frac{1}{2}}\right]^{\frac{1}{2}} \\b=\left[\frac{2\left(\mu_{20}+\mu_{02}-\sqrt{\left(\mu_{20}-\mu_{02}\right)^{2}+4 \mu_{11}^{2}}\right.}{\mu_{00}}\right]^{\frac{1}{2}}\end{array}\right. ⎩ ⎨ ⎧a=[μ002(μ20+μ02+(μ20−μ02)2+4μ112)21]21 21b=[μ002(μ20+μ02−(μ20−μ02)2+4μ112]21
D:偏心率
偏心率:是描述椭圆形状的一个指标,它表示椭圆离开圆形的程度。偏心率越接近于0,表示椭圆形状越接近于圆形;而偏心率越接近于1,表示椭圆形状越拉长。在几何学中,偏心率可以通过椭圆的焦点和半长轴之间的比例来定义
e = a b e=\frac{a}{b} e=ba
相关文章:

(数字图像处理MATLAB+Python)第十一章图像描述与分析-第五、六节:边界描述和矩描述
文章目录 一:边界描述(1)边界链码A:概述B:边界链码改进C:程序 (2)傅里叶描绘子A:概述B:程序 二:矩描述(1)矩A:…...
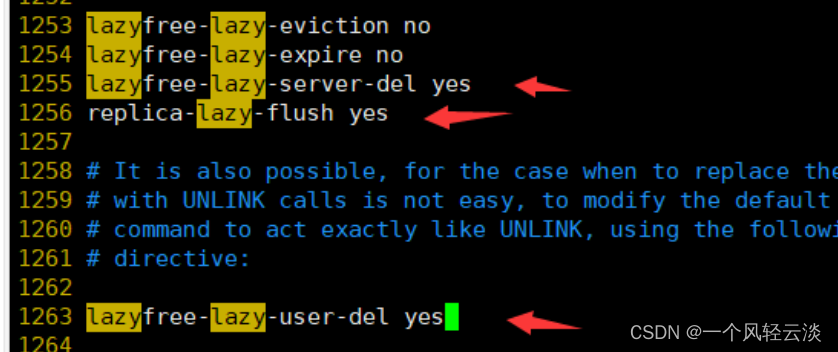
Redis之bigkey问题解读
目录 什么是bigkey? bigkey引发的问题 如何查找bigkey redis-cli --bigkeys MEMORY USAGE bigKey如何删除 渐进式删除 unlink bigKey生产调优 什么是bigkey? bigkey简单来说就是存储本身的key值空间太大,或者hash,list&…...

ElementUI浅尝辄止27:Steps 步骤条
引导用户按照流程完成任务的分步导航条,可根据实际应用场景设定步骤,步骤不得少于 2 步。 1.如何使用? 设置active属性,接受一个Number,表明步骤的 index,从 0 开始。需要定宽的步骤条时,设置s…...

React 18 迁移状态逻辑至 Reducer 中
参考文章 迁移状态逻辑至 Reducer 中 对于拥有许多状态更新逻辑的组件来说,过于分散的事件处理程序可能会令人不知所措。对于这种情况,可以将组件的所有状态更新逻辑整合到一个外部函数中,这个函数叫作 reducer。 使用 reducer 整合状态逻…...
 函数 源代码流程分析)
【SA8295P 源码分析】89 - QNX AIS Camera qcarcam_test 可执行程序 main() 函数 源代码流程分析
【SA8295P 源码分析】89 - QNX AIS Camera qcarcam_test 可执行程序 main 函数 源代码流程分析 一、qcarcam_test.cpp main() 函数源码分析二、qcarcam_test_setup_input_ctxt_thread( ) :初始化 gCtxt.inputs[input_idx] 上下文环境三、process_cb_event_thread( ) :负责处理…...

STM32屏幕计时器
目录 一、最终效果二、实现思想三、实现过程3.1 屏幕显示3.2 中断处理 一、最终效果 显示屏显示计时时间,格式为 00:00:00,依次为 时:分:秒,程序运行之后自动计时,当按下按键,计时清零,按下按键采用外部中…...
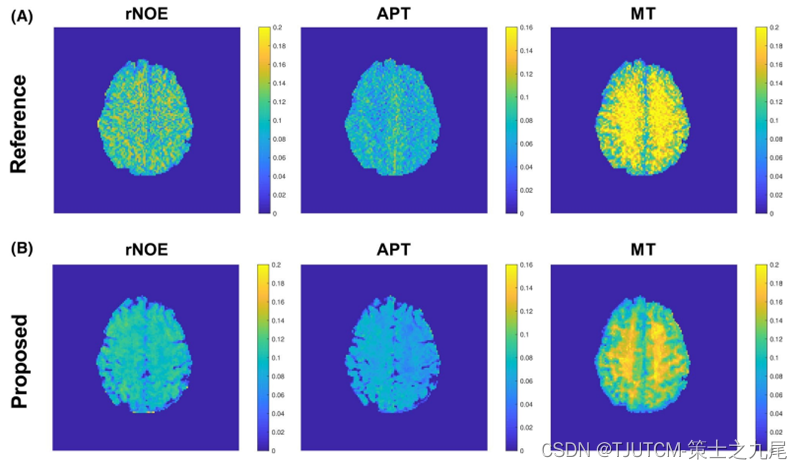
MRI多任务技术及应用
目录 一、定量心血管磁共振成像(CMR)的改进方法二、磁共振多任务三、磁共振多任务的成像框架四、磁共振多任务的图像模型和采样和重建策略五、利用MR多任务进行快速三维稳态CEST(ss-CEST)成像5.1 利用MR多任务进行快速三维稳态CEST(ss-CEST)成像介绍5.2 …...
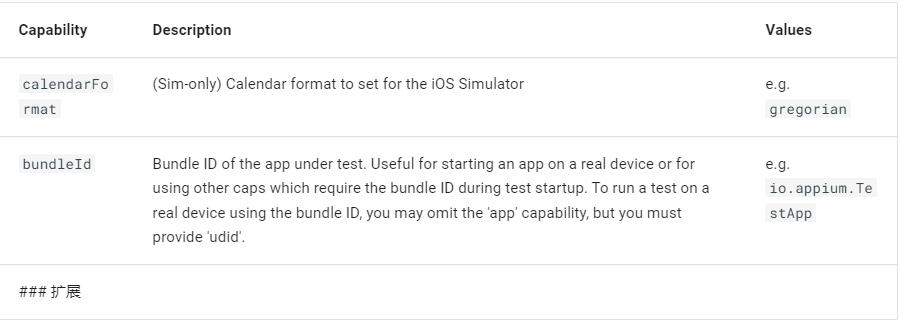
app自动化测试(Android)
Capability 是一组键值对的集合(比如:"platformName": "Android")。Capability 主要用于通知 Appium 服务端建立 Session 需要的信息。客户端使用特定语言生成 Capabilities,最终会以 JSON 对象的形式发送给 …...

【力扣每日一题】2023.9.3 消灭怪物的最大数量
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 题目比较长,我概括一下就是有一群怪物,每只怪物离城市的距离都不一样,并且靠近的速度也不一样&#x…...
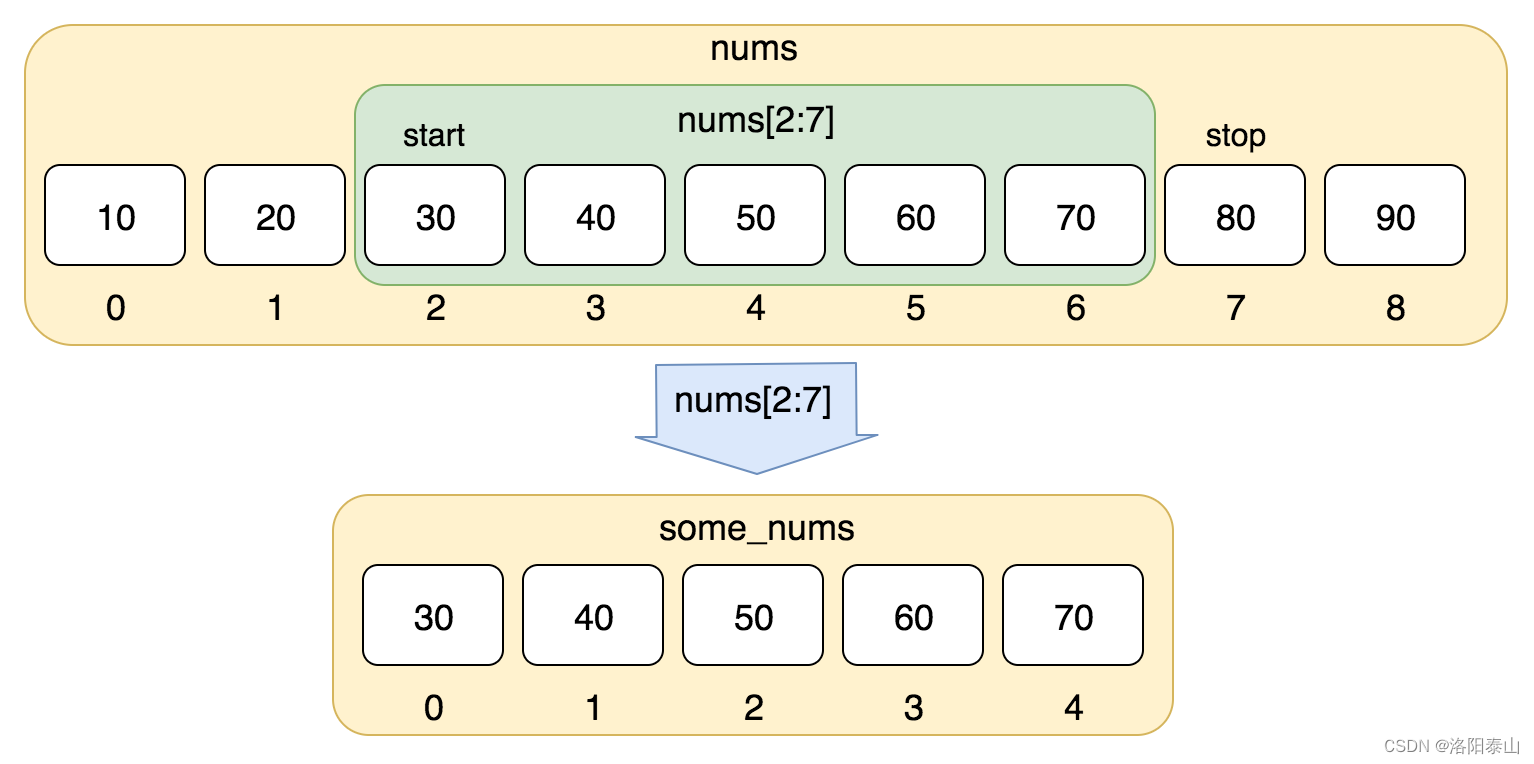
Python入门教程 | Python3 列表(List)
Python3 列表 序列是 Python 中最基本的数据结构。 序列中的每个值都有对应的位置值,称之为索引,第一个索引是 0,第二个索引是 1,依此类推。 Python 有 6 个序列的内置类型,但最常见的是列表和元组。 列表都可以进…...
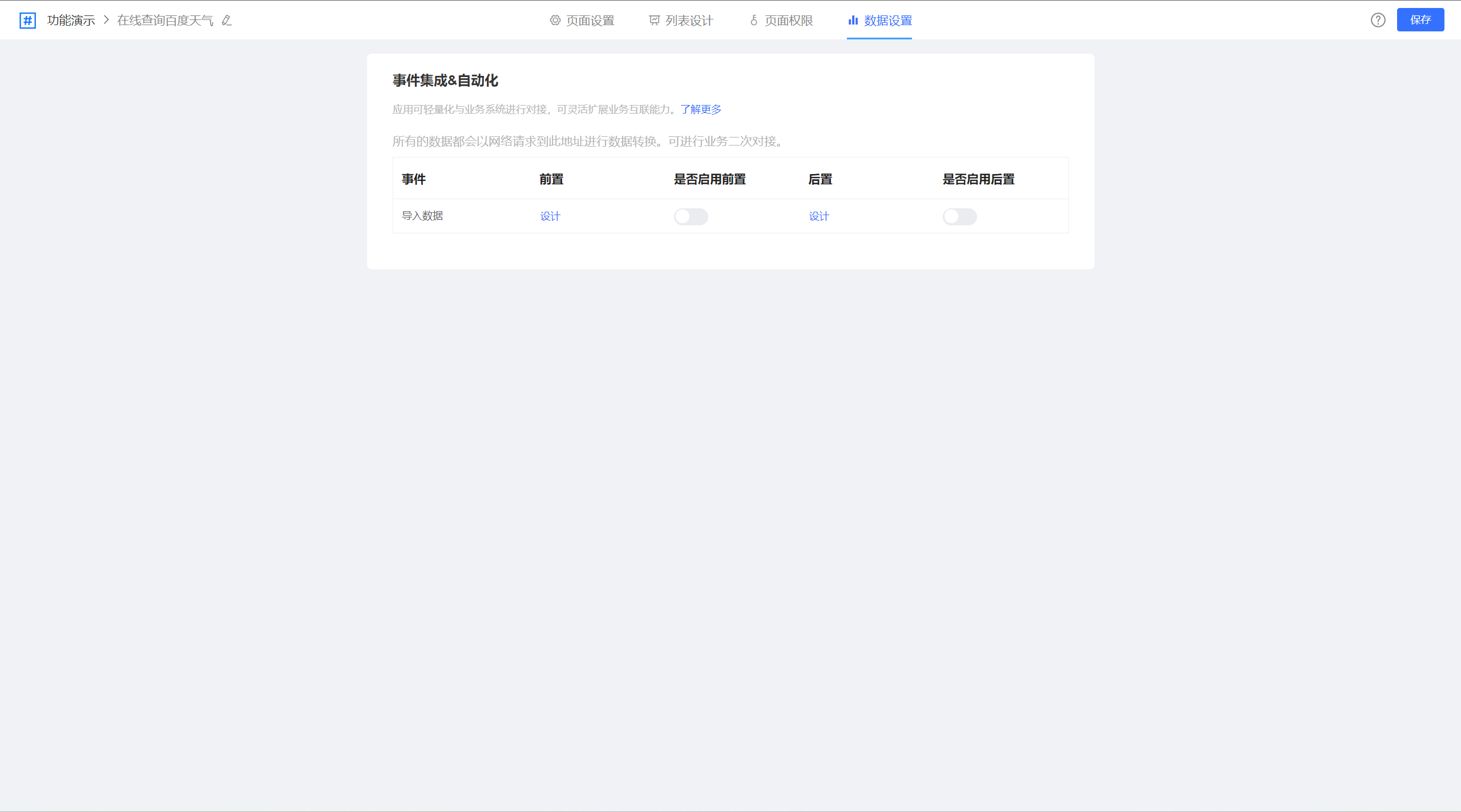
Java低代码开发:jvs-list(列表引擎)功能(一)配置说明
在低代码开发平台中,列表页是一个用于显示数据列表的页面。它通常用于展示数据库中的多条记录,并提供搜索、排序和筛选等功能,以方便用户对数据进行查找和浏览。 jvs-list是jvs快速开发平台的列表页的配置引擎,它和普通的crud 具…...
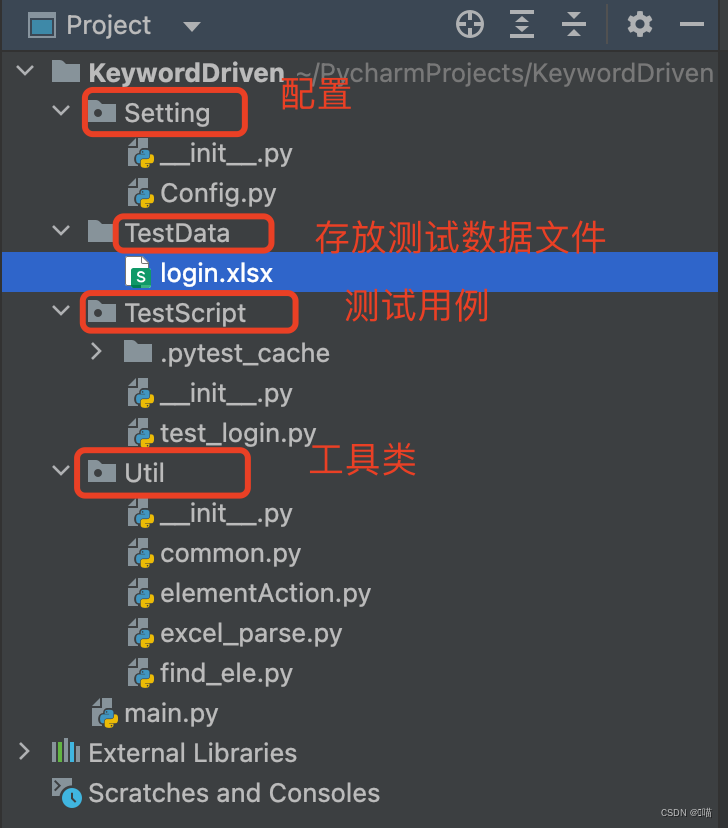
UI自动化之关键字驱动
关键字驱动框架:将每一条测试用例分成四个不同的部分 测试步骤(Test Step):一个测试步骤的描述或者是测试对象的一个操作说明测试步骤中的对象(Test Object):指页面的对象或者元素对象执行的动…...

前端高性能渲染 — 虚拟列表
虚拟列表,实际上就是在首屏加载的时候,只加载可视区域内需要的列表项,当滚动发生时,动态通过计算获得可视区域内的列表项,并将非可视区域内存在的列表项删除。该技术是解决渲染大量数据的一种解决方法。 实现虚拟列表&…...

防水出色的骨传导耳机,更适合户外运动,南卡Runner Pro 4S体验
已经接近尾声的夏季依然酷热,对于运动爱好者来说,这确实也是锻炼的好时机,无论是一会儿就能大汗淋漓的HIIT,还是是各种清凉的水上运动,在健身的同时,戴上一副耳机享受音乐,都会更加痛快一些。 相…...
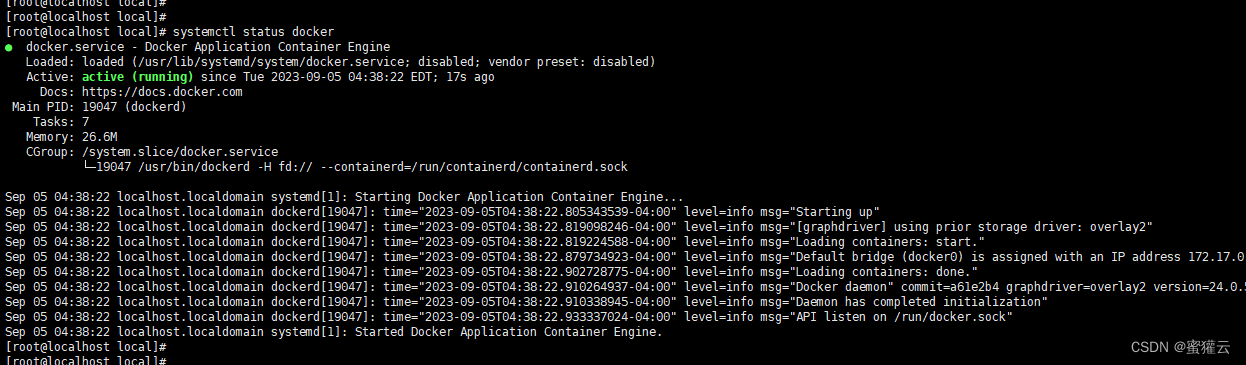
docker快速安装-docker一键安装脚本
1.下载/配置安装脚本 touch install-docker.sh #!/bin/bash #mail:ratelcloudqq.com #system:centos7 #integration: docker-latestclear echo "######################################################" echo "# Auto Install Docker …...
)
1584 - Circular Sequence (UVA)
题目链接如下: Online Judge 我的代码如下: #include <cstdio> #include <string.h> const int maxN 101;int T, len, pivot; char a[maxN];int main(){scanf("%d", &T);for(int i 0; i < T; i){scanf("%s"…...
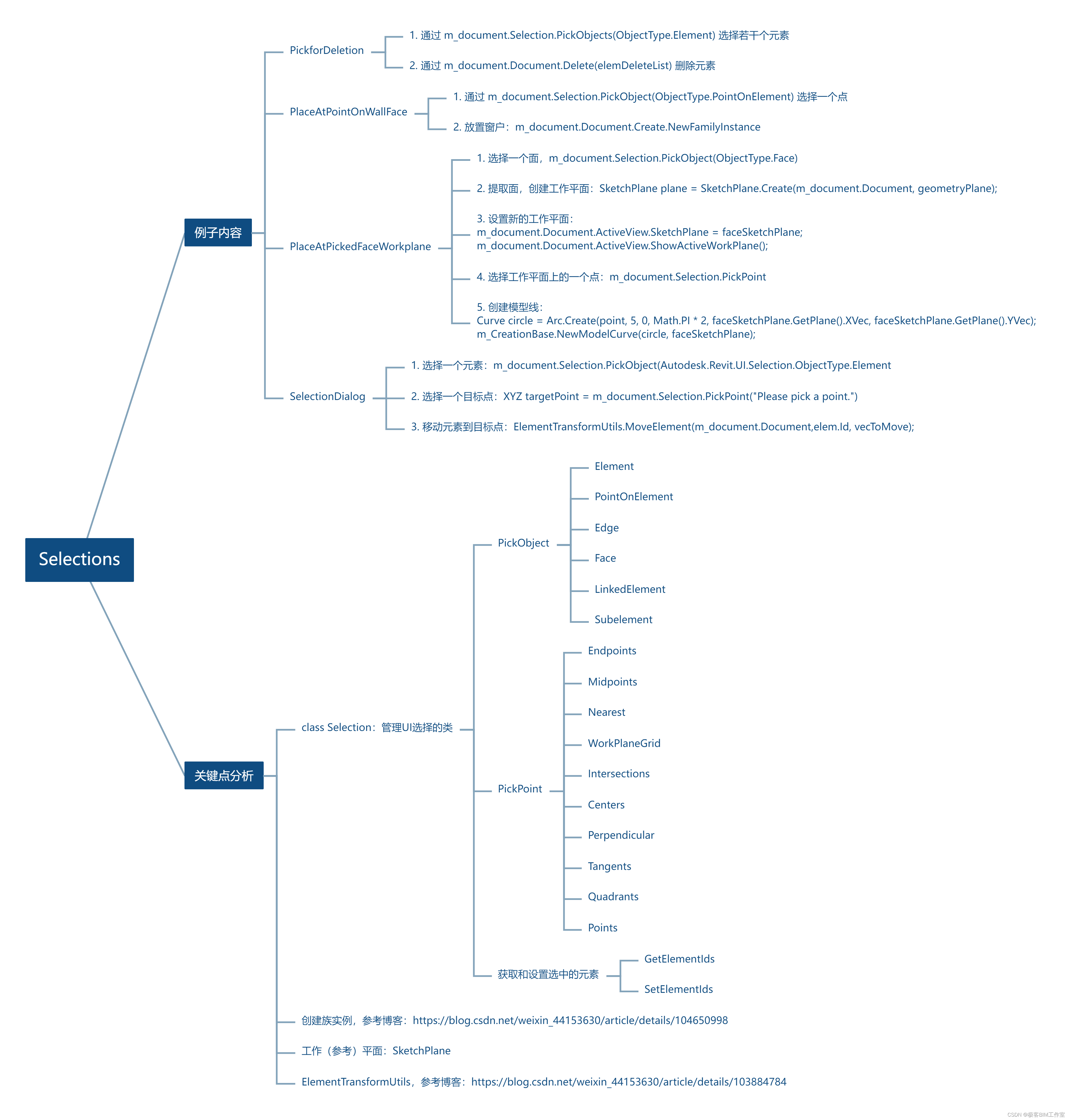
Revit SDK:Selections 选择
前言 Revit 作为一款成熟的商业软件,它将自己的UI选择功能也通过 API 暴露出来。通过 API 可以按照特定的过滤规则来选择相应的元素,能力和UI基本上是等价的。这个 SDK 用四个例子展示了 API 的能力,内容如下。 内容 PickforDeletion 核心…...
)
K8s中的RBAC(Role-Based Access Control)
摘要 RBAC(基于角色的访问控制)是一种在Kubernetes中用于控制用户对资源的访问权限的机制。以下是RBAC的设计实现说明: 角色(Role)和角色绑定(RoleBinding):角色定义了一组权限&am…...
)
肖sir__设计测试用例方法之经验测试方法09_(黑盒测试)
设计测试用例方法之经验测试方法 一、经验的测试技术 (1)基于经验的测试技术之错误推测法 错误推测法也叫错误猜测法,就是根据经验猜想,已有的缺陷,测试经验和失败数据等可能有什么问题并依此设计测试用例 ࿰…...
Python爬虫:下载小红书无水印图片、视频
该代码只提供学习使用,该项目是基于https://github.com/JoeanAmier/XHS_Downloader的小改动 1.下载项目 git clone https://github.com/zhouayi/XHS_Downloader.git2.找到需要下载的文章的ID 写入main.py中 3.下载 python main.py最近很火的莲花楼为例<嘿嘿…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...
