【算法】归并排序 详解
归并排序 详解
- 归并排序
- 代码实现
- 1. 递归版本
- 2. 非递归版本
排序: 排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
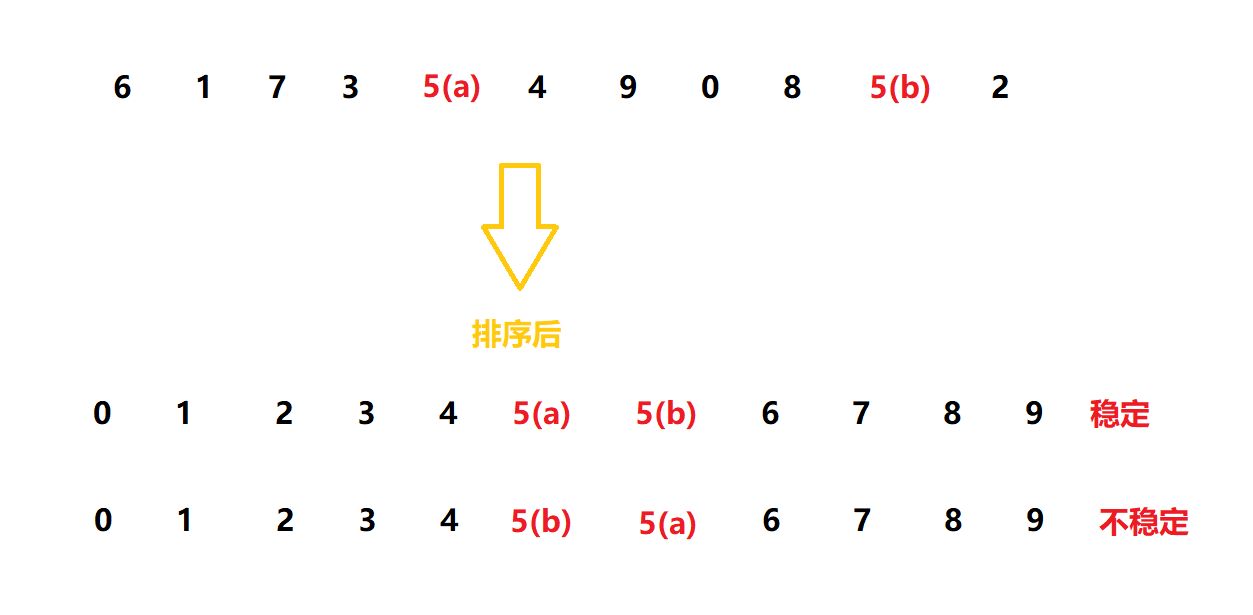
稳定性: 假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中, r[i] = r[j], 且 r[i] 在 r[j] 之前,而在排序后的序列中, r[i] 仍在 r[j] 之前,则称这种排序算法是稳定的;否则称为不稳定的。
(注意稳定排序可以实现为不稳定的形式, 而不稳定的排序实现不了稳定的形式)
内部排序: 数据元素全部放在内存中的排序。
外部排序: 数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
归并排序
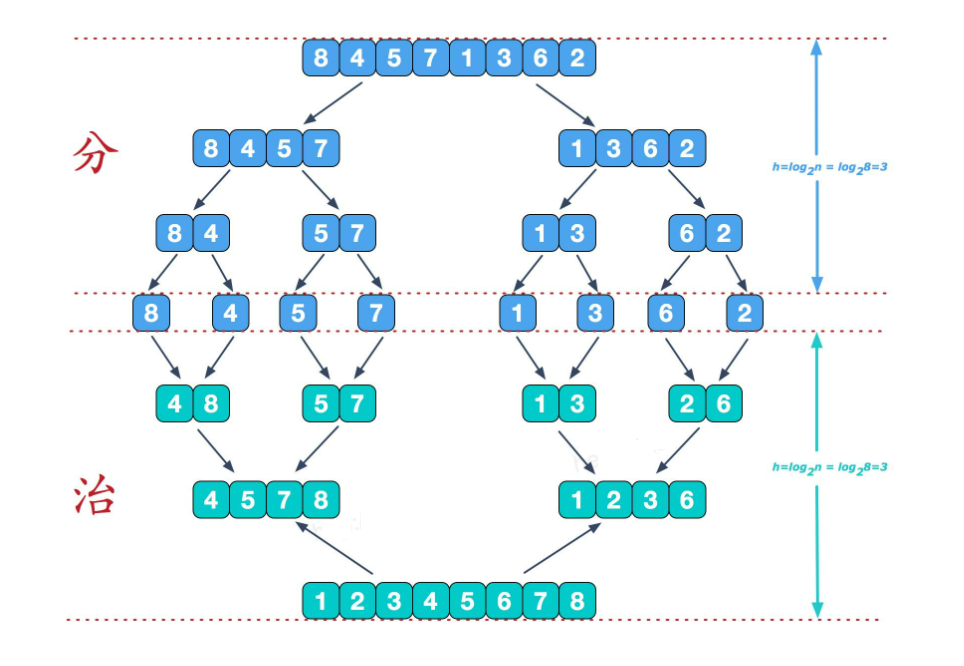
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
- 分解(Divide):将n个元素分成两个个含n/2个元素的子序列。
- 解决(Conquer):用合并排序法对两个子序列递归的排序。
- 合并(Combine):合并两个已排序的子序列已得到排序结果。
代码实现
1. 递归版本
public static void mergeSort(int[] arr) {int len = arr.length;partition(arr, 0, len-1);}public static void partition(int[] arr, int left, int right) {if (left >= right) {return;}// 将区间分成左右两个部分, 并将两个部分分别排序int mid = ((right-left) >> 1) + left;partition(arr, left, mid);partition(arr, mid+1, right);// 将两部分合并int[] temp = new int[right-left+1];int index = 0;int index1 = left;int index2 = mid+1;while (index1 <= mid && index2 <= right) {if (arr[index1] < arr[index2]) {temp[index++] = arr[index1++];} else {temp[index++] = arr[index2++];}}while (index1 <= mid) {temp[index++] = arr[index1++];}while (index2 <= right) {temp[index++] = arr[index2++];}// 重新拷贝回去for (int i = 0; i < index; i++) {arr[left+i] = temp[i];}}
2. 非递归版本
public static void mergeSortNonR(int[] arr) {int len = arr.length;// i 表示的是, 左右区间中每个区间的元素个数for (int i = 1; i < len; i*=2) {// j 每次要跳过两个区间for (int j = 0; j < len; j += 2*i) {int left1 = j;int right1 = j + i - 1;int left2 = right1 + 1;int right2 = left2 + i - 1;// 修正一下 right1, right2, 因为可能 right1 和 right2 越界了if (right1 >= len) {right1 = len-1;}if (right2 >= len) {right2 = len - 1;}// 开始合并int[] temp = new int[2*i];int index = 0;while (left1 <= right1 && left2 <= right2) {if (arr[left1] <= arr[left2]) {temp[index++] = arr[left1++];} else {temp[index++] = arr[left2++];}}while (left1 <= right1) {temp[index++] = arr[left1++];}while (left2 <= right2) {temp[index++] = arr[left2++];}// 拷贝回去for (int k = 0; k < index; k++) {arr[j+k] = temp[k];}}}}
总结:
- 时间复杂度: O(N*logN)
- 空间复杂度: O(N)
- 是稳定排序
- 对数据不敏感: 不管数据原本怎么排列, 都需要先分解, 然后归并。
- 归并的缺点在于需要 O(N) 的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
海量数据的排序问题
假设条件为:内存只有 1G,需要排序的数据有 100G
因为内存中因为无法把所有数据全部放下,所以需要外部排序,而归并排序是最常用的外部排序
- 先把文件切分成 200 份,每个 512 M
- 分别对 512 M 排序,因为内存已经可以放的下,所以任意排序方式都可以
- 进行 2 路归并,同时对 200 份有序文件做归并过程,最终结果就有序了
以上就是对归并排序的讲解, 希望能帮到你 !
评论区欢迎指正 !
相关文章:

【算法】归并排序 详解
归并排序 详解 归并排序代码实现1. 递归版本2. 非递归版本 排序: 排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。 稳定性: 假定在待排序的记录序列中,存在多个具有相…...

linux 进程隔离Namespace 学习
一、linux namespace 介绍 1.1、概念 Linux Namespace是Linux内核提供的一种机制,它用于隔离不同进程的资源视图,使得每个进程都拥有独立的资源空间,从而实现进程之间的隔离和资源管理。 Linux Namespace的设计目标是为了解决多个进程之间…...
【MySQL】事务 详解
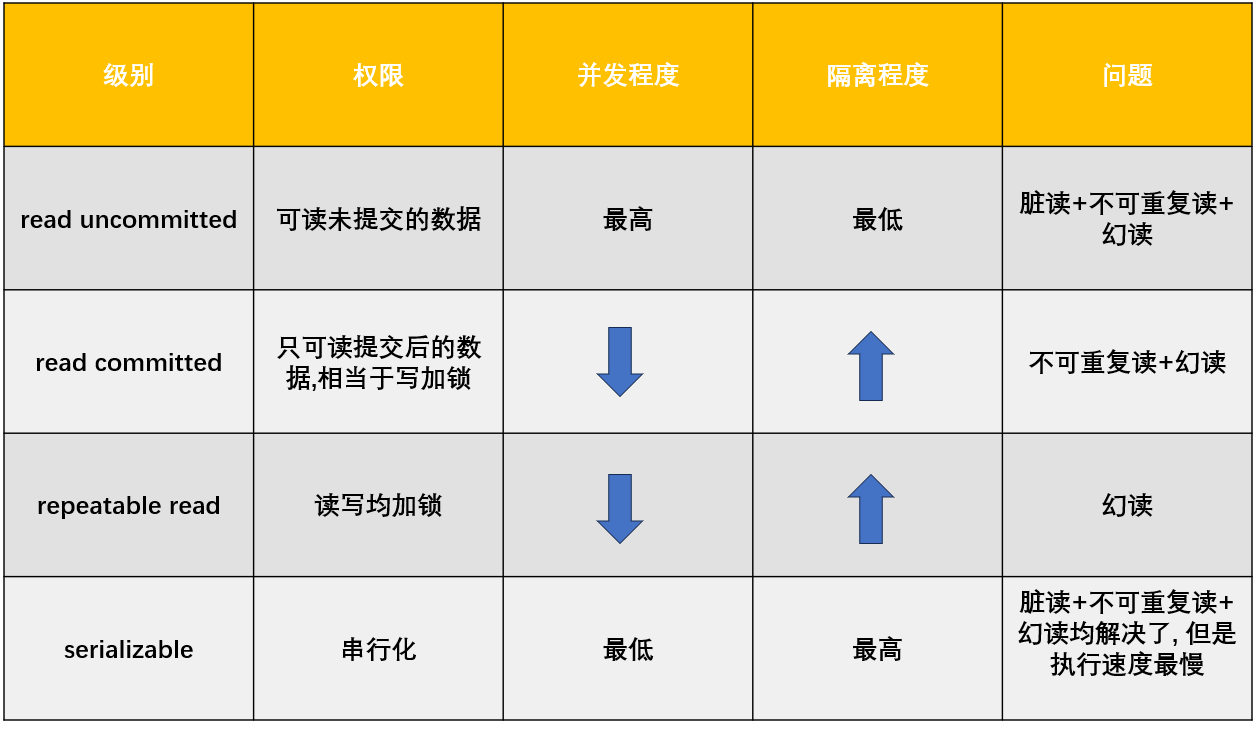
事务 详解 一. 为什么使用事务二. 事务的概念三. 使用四. 事务的特性原子性(Atomicity)一致性(Consistency)隔离性(Isolation)持久性(Durability) 五. 事务并发所带来的问题脏读问题…...

爬虫到底难在哪里?
目录 爬虫到底难在哪里 怎么学习爬虫 注意事项 爬虫工具 总结 学习Python爬虫的难易程度因人而异,对于具备编程基础的人来说,学习Python爬虫并不困难。Python语言本身比较简单易学,适合初学者使用。 爬虫到底难在哪里 爬虫的难点主要包…...

linux常用命令行整理
1、linux的以及目录 bin 二进制可执行文件sbin 二进制可执行文件(root用户权限)etc 系统管理和配置文件,例如常见host文件home 用户文件的根目录usr 用户存放系统应用程序(共享系统资源)opt 可选的应用程序proc 虚拟文件系统root 超级用户dev 存放设备文件mnt 系统管理员安装临…...

python字符串相关
python字符串相关 一、reverse() 函数 只能反转 列表二、reversed() 反转元组字符串等等 返回迭代器三、join和reversed反转字符串四、join串联字符串(join连接对象仅限字符串、储存字符串的元组、列表、字典)数字对象可通过str()转化为字符串⭐对象为字…...

JavaScript学习笔记01
JavaScript笔记01 什么是 JavaScript JavaScript 是一门世界上最流行的脚本语言,它是一种弱类型的脚本语言,其代码不需要经过编译,而是由浏览器解释运行,用于控制网页的行为。 发展历史 参考:JavaScript的起源故事…...
golang 通用的 grpc http 基础开发框架
go-moda golang 通用的 grpc http 基础开发框架仓库地址: https://github.com/webws/go-moda仓库一直在更新,欢迎大家吐槽和指点 特性 transport: 集成 http(echo、gin)和 grpc。tracing: openTelemetry 实现微务链路追踪pprof: 分析性能config: 通用…...
FSK解调技术的FPGA实现
本原创文章由深圳市小眼睛科技有限公司创作,版权归本公司所有,如需转载,需授权并注明出处 一、FSK信号的解调原理 FSK信号的解调也有非相干和相干两种,FSK信号可以看作是用两个频率源交替传输得到的,所以FSK的接收机由…...
Matlab图像处理-高斯低通滤波器
高通滤波 图像的边缘、细节主要位于高频部分,而图像的模糊是由于高频成分比较弱产生的。高通滤波就是为了高消除模糊,突出边缘。因此采用高通滤波器让高频成分通过,消除低频噪声成分削弱,再经傅里叶逆变换得到边缘锐化的图像。 …...
文件上传之图片马混淆绕过与条件竞争
一、图片马混淆绕过 1.上传gif imagecreatefromxxxx函数把图片内容打散,,但是不会影响图片正常显示 $is_upload false; $msg null; if (isset($_POST[submit])){// 获得上传文件的基本信息,文件名,类型,大小&…...

代码随想录二刷day16
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣104. 二叉树的最大深度二、力扣559. N 叉树的最大深度三、力扣111. 二叉树的最小深度三、力扣力扣222. 完全二叉树的节点个数 前言 一、力扣104. 二叉树…...

【开发】安防监控/视频存储/视频汇聚平台EasyCVR优化播放体验的小tips
视频云存储/安防监控EasyCVR视频汇聚平台基于云边端智能协同,可实现视频监控直播、视频轮播、视频录像、云存储、回放与检索、智能告警、服务器集群、语音对讲、云台控制、电子地图、H.265自动转码H.264、平台级联等。为了便于用户二次开发、调用与集成,…...
算法_C++—— 只出现一次的数字)
力扣(LeetCode)算法_C++—— 只出现一次的数字
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。 你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。 示例 1 : 输入࿱…...
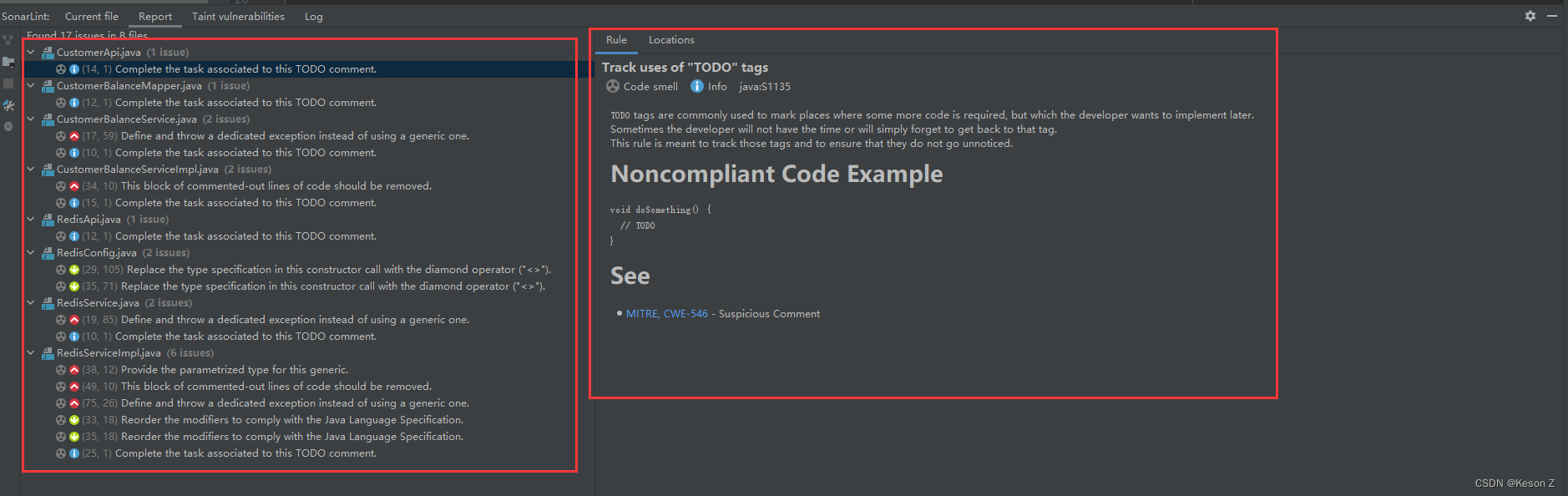
Windows配置SonarQube代码审查工具详细步骤(附带IDEA SonarLint插件使用)
文章目录 环境说明以及准备一. SonarQube的下载与安装二. 添加SonarQube项目三. 使用Maven命令上传代码到SonarQube四. IDEA安装SonarLint插件 环境说明以及准备 本篇博客使用的SonarQube版本为9.8,注意JDK 1.8已经不能支持 NameVersionDownLoad LinkSonarQube9.8…...

【Unity3D】UI Toolkit元素
1 前言 UI Toolkit简介 中介绍了 UI Builder、样式属性、UQuery、Debugger,UI Toolkit容器 中介绍了 VisualElement、ScrollView、ListView、GroupBox 等容器,UI Toolkit样式选择器 中介绍了简单选择器、复杂选择器、伪类选择器等样式选择器,…...
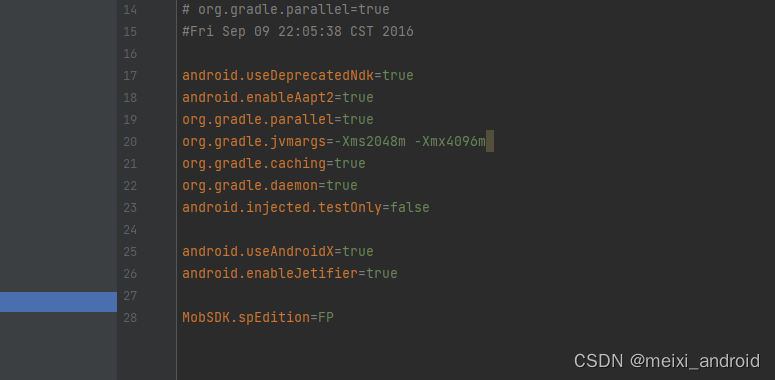
Task :app:compileDebugKotlin FAILED
gradle.properties 里面加上 android.enableJetifiertrue...

Android——数据存储(一)(二十一)
1. 数据存储 1.1 知识点 (1)掌握Android数据存储的分类; (2)可以使用SharedPreferences存储数据。 1.2 具体内容 对于我们数据的存储而言,Android一共提供了5个数据存储的方式:SharedPrefe…...

机器学习课后习题 ---数学基础回顾
(一)选择题 1.函数y=1/(x+1)是 A.偶函数 B.奇函数 C.单调函数 D.无界函数 2.设f(sin(x/2)=cosx+1,则f(x)为() A.2x-2 B.2-2x C.1+2 …...
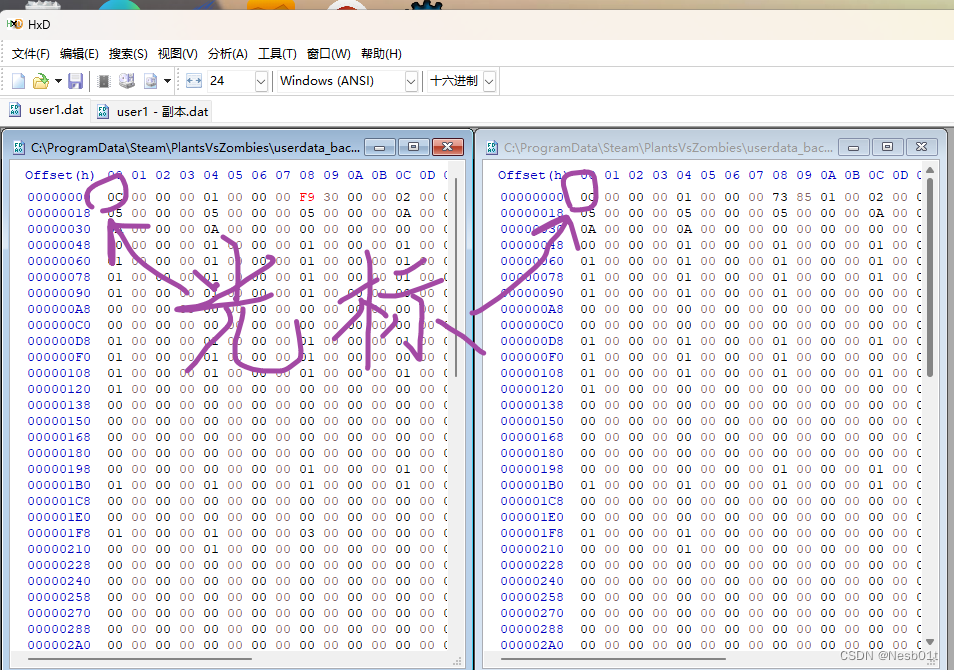
CS420 课程笔记 P4 - 以16进制形态编辑游戏文件
文章目录 IntroductionFinding save filesStringsUnicodeExample!Value searchHealth searchConclusion Introduction 这节课我们将学习编辑十六进制,主要用于编辑保存文件,但十六进制编辑涉及的技能可以很好地转移到: Save file editingRe…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...

Linux基础开发工具——vim工具
文章目录 vim工具什么是vimvim的多模式和使用vim的基础模式vim的三种基础模式三种模式的初步了解 常用模式的详细讲解插入模式命令模式模式转化光标的移动文本的编辑 底行模式替换模式视图模式总结 使用vim的小技巧vim的配置(了解) vim工具 本文章仍然是继续讲解Linux系统下的…...
