线段树总结
文章目录
- 参考文档
- 题目
- 线段树实现
- 单点修改,区间求值
- 模板题目
- 308. 二维区域和检索 - 可变
- 区间修改,区间求值
- 1. 掉落的方块(区间开点)
- 2. 维护序列
- 3. 一个简单的问题2
- 4. 天际线问题
- 动态开点
- 1. 区间和个数(单点修改开点)
- 问题以及注意事项
参考文档
线段树动态开点java
动态开点c++
线段树leetcode题目
题目
| 题目 | 知识点/注意点 | 难度 |
|---|---|---|
| 更新数组后处理求和查询 | 线段树 | 困难 |
| 维护序列 | 区间修改、求和 | 困难 |
| 掉落的方块 | 右边区间-1 | 困难 |
| leetcode 气球颜色变换 | 右边区间-1 | |
| leetcode 218.天际线 | 右边区间-1 | 困难 |
| leetcode 307. 区域和检索 - 数组可修改 | 下标开始的位置 | 困难 |
| leetcode 315. 计算右侧小于当前元素的个数 | 保证r >= l | 困难 |
| leetcode 493. 翻转对 | 离散化 / 动态开点 | 困难 |
| leetcode 327. 区间和的个数 | 离散化 / 动态开点 | 困难 |
线段树实现
- 一般Push_down和push_up是需要手动实现的。
- 注意下标从1开始,build和使用的时候需要注意。
- 动态开点的时候,push_down和update会动态开点。
- 使用的时候,需要保证r >= l,否则会出现各种问题。
- 动态开点的时候,需要保证(l, r)的范围包含全部点。
单点修改,区间求值
模板题目
static const int maxn = 4e5 + 4;int sum[maxn];int n;void push_up(int u) {sum[u] = sum[u << 1] + sum[u << 1 | 1];}void build(int u, int l, int r, vector<int>&nums) {if (l == r) {sum[u] = nums[l - 1];return ;}int mid = (l + r) >> 1;build(u << 1, l, mid, nums);build(u << 1 | 1, mid + 1, r, nums);push_up(u);}void update(int u, int l, int r, int p, int x) {if (p == l && l == r) {sum[u] = x;return ;}int mid = (l + r) >> 1;if (p <= mid) update(u << 1, l, mid, p, x);else update(u << 1 | 1, mid + 1, r, p, x);push_up(u);}int query(int u, int l, int r, int L, int R) {if (L <= l && r <= R) {return sum[u];}int mid = (l + r) >> 1;int ans = 0;if (L <= mid) ans = query(u << 1, l, mid, L, R);if (R > mid) ans += query(u << 1 | 1, mid + 1, r, L, R);return ans; }
308. 二维区域和检索 - 可变
class Solution {
public:// 加是不行的。为什么呢?因为区间[l, r]上的高度不统一。static const int N = 1e6 + 10;int maxh[N], lc[N], rc[N], idx = 0, root = 0; // root应该写成全局变量,int lazy[N];// int add[N]; // 区间同时增加高度不行void push_up(int u) {maxh[u] = max(maxh[lc[u]], maxh[rc[u]]);}// 将区间,改编成add_h。如果没有区间就开点void push_down(int &u, int x) {if (!u) u = ++idx; // push_down的时候也需要创建新的lazy[u] = maxh[u] = x;}// 懒标记下推void push_down(int u) {// if (add[u] == 0) return ;if (lazy[u] == 0) return ;push_down(lc[u], lazy[u]);push_down(rc[u], lazy[u]);lazy[u] = 0; // 清除懒标记}// [L, R]增加add_x, 需要加上引用,让lc和rc指向正确位置。void update(int &u, int l, int r, int L, int R, int add_x) {if (u == 0) u = ++idx; // 给儿子创建一个新的点if (L <= l && r <= R) {push_down(u, add_x);// printf("add_x = %d\n", add_x);return ;}push_down(u);int mid = (l + r) >> 1;// printf("mid = %d l = %d r = %d, L = %d, R = %d\n", mid, l, r, L, R);if (L <= mid) update(lc[u], l, mid, L, R, add_x);if (R > mid) update(rc[u], mid + 1, r, L, R, add_x);push_up(u); // 没有传递u, 所以u不会变}// 询问,不用加引用int query(int u, int l, int r, int L, int R) {if (u == 0) return 0; // 如果没更新这个区间直接返回if (L <= l && r <= R) {return maxh[u];}push_down(u);int mid = (l + r) >> 1;int maxv = 0;// printf("%d %d %d %d %d\n", mid, l, r, L, R);if (L <= mid) maxv = query(lc[u], l, mid, L, R);if (R > mid) maxv = max(maxv, query(rc[u], mid + 1, r, L, R));return maxv;}vector<int> fallingSquares(vector<vector<int>>& positions) {vector<int>ans;for (auto vec : positions) {int l = vec[0], r = vec[0] + vec[1] - 1, z = vec[1];int cur = query(root, 1, 1e9, l, r);// printf("cur = %d\n", cur);update(root, 1, 1e9, l, r, z + cur);ans.push_back(maxh[1]);}return ans;}
};
区间修改,区间求值
1. 掉落的方块(区间开点)
大区间
少查询
动态开点: 使用指针的进行开点
离散化
int x = info[0], h = info[1], cur = query(1, 1, N, x, x + h - 1);
查询 – [x, x + h - 1]
修改 – [x, x + h - 1, cur + h]
当前的最大值就是tr[1].val
class Solution {
public:// 加是不行的。为什么呢?因为区间[l, r]上的高度不统一。static const int N = 1e6 + 10;int maxh[N], lc[N], rc[N], idx = 0, root = 0; // root应该写成全局变量,int lazy[N];// int add[N]; // 区间同时增加高度不行void push_up(int u) {maxh[u] = max(maxh[lc[u]], maxh[rc[u]]);}// 将区间,改编成add_h。如果没有区间就开点void push_down(int &u, int x) {if (!u) u = ++idx; // push_down的时候也需要创建新的lazy[u] = maxh[u] = x;}// 懒标记下推void push_down(int u) {// if (add[u] == 0) return ;if (lazy[u] == 0) return ;push_down(lc[u], lazy[u]);push_down(rc[u], lazy[u]);lazy[u] = 0; // 清除懒标记}// [L, R]增加add_xvoid update(int &u, int l, int r, int L, int R, int add_x) {if (u == 0) u = ++idx; // 给儿子创建一个新的点if (L <= l && r <= R) {push_down(u, add_x);// printf("add_x = %d\n", add_x);return ;}push_down(u);int mid = (l + r) >> 1;// printf("mid = %d l = %d r = %d, L = %d, R = %d\n", mid, l, r, L, R);if (L <= mid) update(lc[u], l, mid, L, R, add_x);if (R > mid) update(rc[u], mid + 1, r, L, R, add_x);push_up(u); // 没有传递u, 所以u不会变}int query(int &u, int l, int r, int L, int R) {if (u == 0) return 0; // 如果没更新这个区间直接返回if (L <= l && r <= R) {return maxh[u];}push_down(u);int mid = (l + r) >> 1;int maxv = 0;// printf("%d %d %d %d %d\n", mid, l, r, L, R);if (L <= mid) maxv = query(lc[u], l, mid, L, R);if (R > mid) maxv = max(maxv, query(rc[u], mid + 1, r, L, R));return maxv;}vector<int> fallingSquares(vector<vector<int>>& positions) {vector<int>ans;for (auto vec : positions) {int l = vec[0], r = vec[0] + vec[1] - 1, z = vec[1];int cur = query(root, 1, 1e9, l, r);// printf("cur = %d\n", cur);update(root, 1, 1e9, l, r, z + cur);ans.push_back(maxh[1]);}return ans;}
};
- 问题1:为什么动态开点不判断u是否为空?询问直接返回就行了,更新的时候需要判断。
- 问题2:直接把val赋值成为add,是否都是这样?还是仅仅是这个题目这样?仅仅这个题目这样。
2. 维护序列
调试技巧
- 首先判断build是否成功
- 其次判断询问是否成功
- 最后根据根节点的信息判断更新是否成功。
- push_down和push_up可以输出前后的sum[u]进行判断
3. 一个简单的问题2
java代码再acwnig的java代码上。
- long的使用
- 两个push_down
- 一个push_down是下推
- 另一个是更新区间的sum和懒标记
4. 天际线问题
class NumMatrix {
public:// 每一行使用一个线段树来维护static const int MAXN = 8e4 + 4;static const int N = 3e2 + 4;int sum[N][MAXN];vector<vector<int>>nums;int m, n;void push_up(int row, int u) {sum[row][u] = sum[row][u << 1] + sum[row][u << 1 | 1];}void build(int row, int u, int l, int r) {if (l == r) {sum[row][u] = nums[row][l - 1];return ;}int mid = (l + r) >> 1;// printf("%d %d %d\n", l, r, mid);build(row, u << 1, l, mid);build(row, u << 1 | 1, mid + 1, r);push_up(row, u);}void update(int u, int l, int r, int row, int col, int x) {if (l == r && col == l) { // l == r的时候col一定等于lsum[row][u] = x;return ;}int mid = (l + r) >> 1;if (col <= mid) update(u << 1, l, mid, row, col, x);else update(u << 1 | 1, mid + 1, r, row, col, x);push_up(row, u);}int query(int u, int l, int r, int row, int L, int R) {if (L <= l && r <= R) {return sum[row][u];}int mid = (l + r) >> 1;int ans = 0;if (L <= mid) ans += query(u << 1, l, mid, row, L, R);if (R > mid) ans += query(u << 1 | 1, mid + 1, r, row, L, R);return ans; }NumMatrix(vector<vector<int>>& matrix) {this->nums = matrix;m = nums.size();n = nums[0].size();for (int i = 0; i < m; i++) {build(i, 1, 1, n);// printf("%d\n", sum[i][1]);}}void update(int row, int col, int val) {col++;update(1, 1, n, row, col, val);}int sumRegion(int row1, int col1, int row2, int col2) {int ans = 0;col1++, col2++;for (int i = row1; i <= row2; i++) {ans += query(1, 1, n, i, col1, col2);}return ans;}
};/*** Your NumMatrix object will be instantiated and called as such:* NumMatrix* obj = new NumMatrix(matrix);* obj->update(row,col,val);* int param_2 = obj->sumRegion(row1,col1,row2,col2);*/
动态开点
1. 区间和个数(单点修改开点)
- 注意求最大和最小值的过程
- 注意前缀和为0的情况需要加入进去。而前缀和为0的时候,不用考虑query,因为一定为0,所有的点都是0。
typedef long long LL;static const int N = 4e6 + 10; // 开太小了也爆栈LL add[N];int idx = 0, root = 0, lc[N], rc[N];void push_up(int u) {add[u] = add[lc[u]] + add[rc[u]]; // 如果使用node,可能会出现点不存在的情况,但是这里并不会,因为add[0] = 0;}// 单点修改开点void update(int &u, LL l, LL r, LL p) {if (!u) u = ++idx;// add[u]++; // 直接相当于push_up了if (l == r && l == p) {add[u] += 1;return ;} LL mid = (l + r) >> 1;if (p <= mid) update(lc[u], l, mid, p);else update(rc[u], mid + 1, r, p);push_up(u);}LL query(int u, LL l, LL r, LL L, LL R) {if (!u) return 0;if (L <= l && r <= R) return add[u];LL mid = (l + r) >> 1;LL ans = 0;if (L <= mid) ans += query(lc[u], l, mid, L, R);if (R > mid) ans += query(rc[u], mid + 1, r, L, R);return ans;}int countRangeSum(vector<int>& nums, int low, int high) {int n = nums.size();LL ans = 0;vector<LL>sum(n + 1);sum[0] = 0;memset(lc, 0, sizeof lc);memset(rc, 0 ,sizeof rc);for (int i = 1; i <= n; i++) {sum[i] = sum[i - 1] + nums[i - 1];}LL minv = LLONG_MAX, maxv = LLONG_MIN;for (LL x: sum) {minv = min({minv, x, x - high});maxv = max({maxv, x, x - high});}// cout << minv << " " << maxv << endl;for (LL x: sum) {LL l = x - high, r = x - low;// cout <<x << " " << l << " " << r << endl;ans += query(root, minv, maxv, l, r);// cout << query(root, minv, maxv, l, r) << endl;update(root, minv, maxv, x);}return ans;}
};
问题以及注意事项
- 天际线和方块的问题中,为什么需要右端点-1,而不是左端点 + 1呢?
- 具体的调试技巧,看上面的维护序列。
- 注意使用的时候,区间从1开始,
相关文章:

线段树总结
文章目录参考文档题目线段树实现单点修改,区间求值模板题目308. 二维区域和检索 - 可变区间修改,区间求值1. 掉落的方块(区间开点)2. 维护序列3. 一个简单的问题24. 天际线问题动态开点1. 区间和个数(单点修改开点)问题以及注意事…...
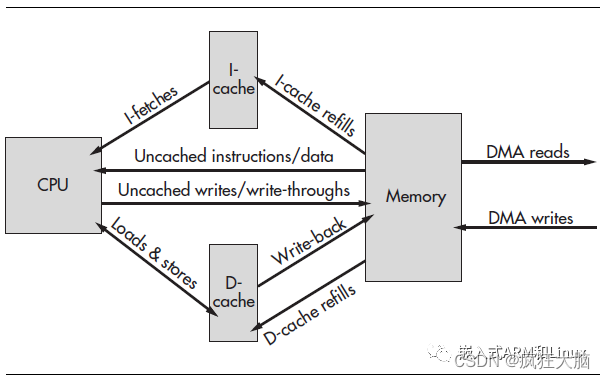
龙芯GS232(MIPS 32)架构cache管理笔记
1 mips32架构 MIPS架构是一种基于精简指令集(Reduced Instruction Set Computer,RISC)的计算机处理器架构。MIPS架构由MIPS Technologies公司在1981年开发,并在1984年发布了第一款MIPS处理器。 MIPS架构的特点包括: …...

js去重
<script>let arr [{ id: 0, name: "张三" },{ id: 1, name: "李四" },{ id: 2, name: "王五" },{ id: 3, name: "赵六" },{ id: 1, name: "孙七" },{ id: 2, name: "周八" },{ id: 2, name: "吴九&qu…...
小白都能看懂的C语言入门教程
文章目录C语言入门教程1. 第一个C语言程序HelloWorld2. C语言的数据类型3. 常量变量的使用4. 自定义标识符#define5. 枚举的使用6. 字符串和转义字符7. 判断和循环8. 函数9. 数组的使用10. 操作符的使用11. 结构体12. 指针的简单使用C语言入门教程 1. 第一个C语言程序HelloWor…...
leetcode 21~30 学习经历
leetcode 21~30 学习经历21. 合并两个有序链表22. 括号生成23. 合并K个升序链表24. 两两交换链表中的节点25. K 个一组翻转链表26. 删除有序数组中的重复项27. 移除元素28. 找出字符串中第一个匹配项的下标29. 两数相除30. 串联所有单词的子串小结21. 合并两个有序链表 将两个升…...

让ArcMap变得更加强大,用python执行地理处理以及编写自定义脚本工具箱
文章目录一、用python执行地理处理工具1.1 例:乘以0.00011.2 例:裁剪栅格1.3 哪里查看调用某工具的代码?二、用python批量执行地理处理工具2.1 必需的python语法知识for循环语句缩进的使用注释的使用2.2 一个批处理栅格的代码模板三、创建自定…...

SAP 项目实施阶段全过程
在sap实施项目的周期和步骤上,根据各公司对业务的理解不同,也被划分为各个阶段,但其中由普华永道提出的分七步走,个人觉得对刚进入这一行业的人很有帮助,接下来一起分享和讨论下: sap实施项目生命周期&…...

idea中的Maven导包失败问题解决总结
idea中的Maven导包失败问题解决总结 先确定idea和Maven 的配置文件settings 没有问题 找到我们本地的maven仓库,默认的maven仓库路径是在\C:\Users\用户名.m2下 有两个文件夹,repositotry是放具体jar包的,根据报错包的名,找对应文…...
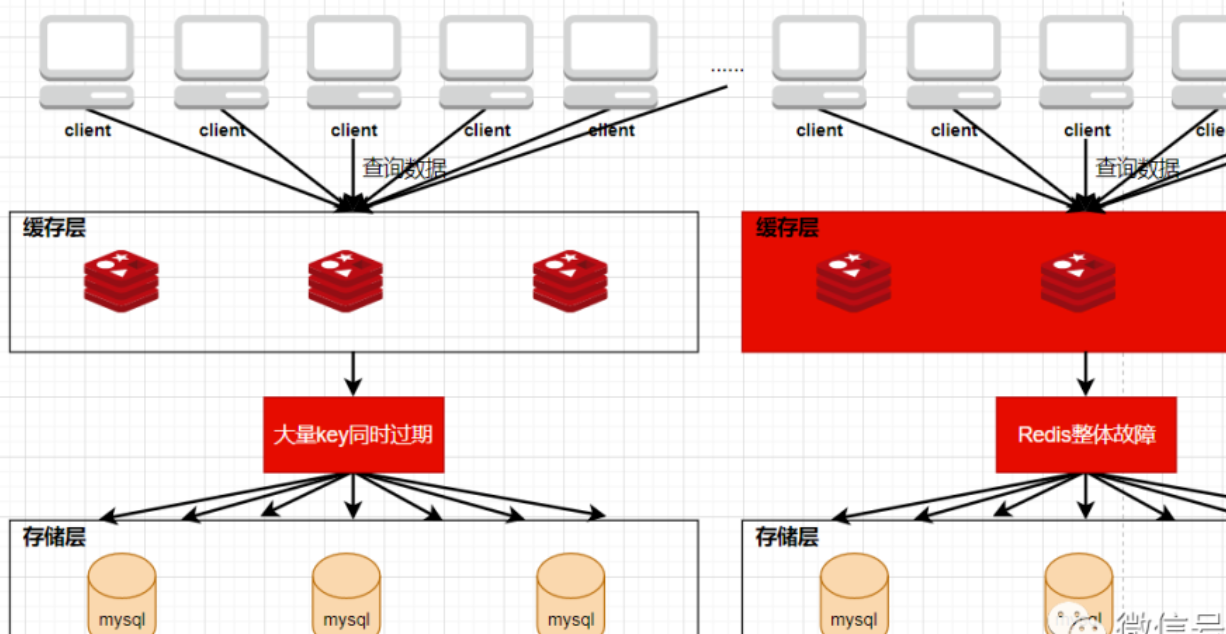
REDIS中的缓存穿透,缓存击穿,缓存雪崩原因以及解决方案
需求引入一般在项目的开发中,都是使用关系型数据库来进行数据的存储,通常不会存在什么高并发的情况,可是一旦涉及大数据量的需求,比如商品抢购,网页活动导致的主页访问量瞬间增大,单一使用关系型数据库来保存数据的系统…...
数据库及缓存之MySQL(一)
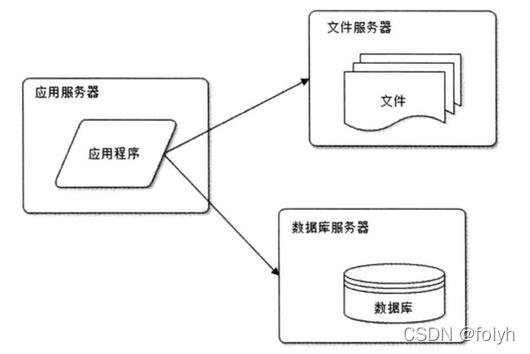
思维导图 常见知识点 1.mysql存储引擎: 2.innodb与myisam区别: 3.表设计字段选择: 4.mysql的varchar(M)最多存储数据: 5.事务基本特性: 6.事务并发引发问题: 7.mysql索引: 8.三星索引…...

项目管理中,项目经理需要具备哪些能力?
项目经理是团队的领导者,是带领项目团队对项目进行策划、执行,完成项目目标,对于项目经理来说,想要有序推进项目,使项目更成功,光有理论知识是不够的,也要具备这些能力: 1、分清主…...

itk中的一些图像处理
文章目录1.BinomialBlurImageFilter计算每个维度上的最近邻居平均值2.高斯平滑3.图像的高阶导数 RecursiveGaussianImageFilter4.均值滤波5.中值滤波6.离散高斯平滑7.曲率驱动流去噪图像 CurvatureFlowImageFilter8.由参数alpha和beta控制的幂律自适应直方图均衡化9.Canny 边缘…...
Endless lseek导致的SQL异常
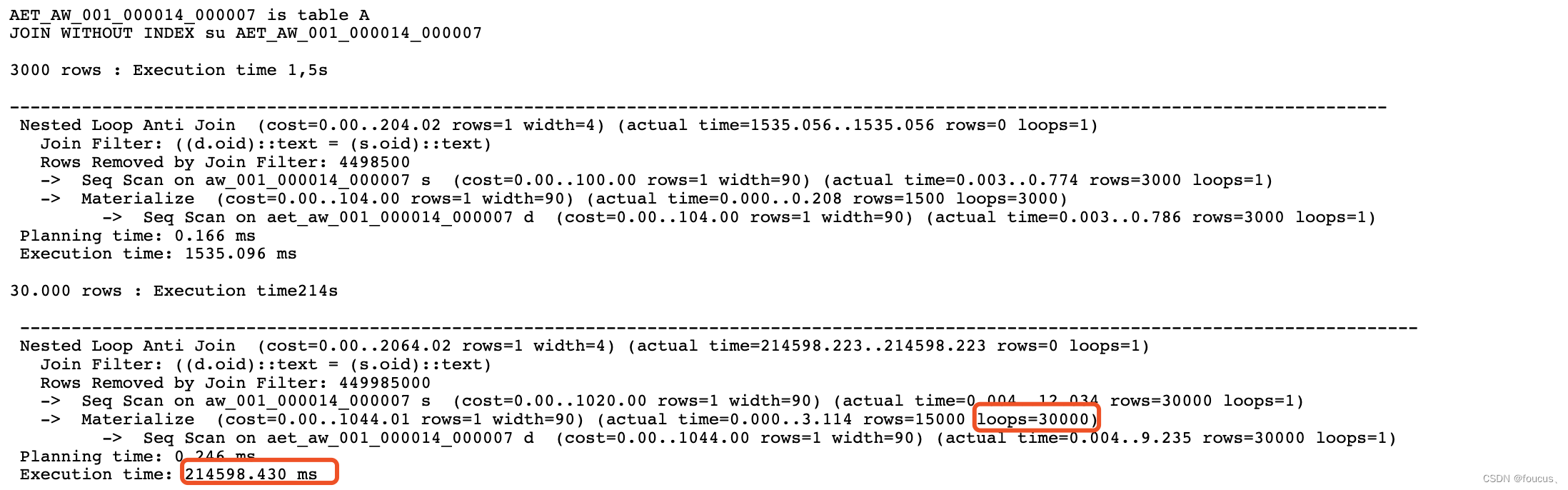
最近碰到同事咨询的一个问题,在执行一个函数时,发现会一直卡在那里。 strace抓了下发现会话一直在执行lseek,大致情况如下: 16:13:55.451832 lseek(33, 0, SEEK_END) 1368064 <0.000037> 16:13:55.477216 lseek(33, 0, SE…...
JUC-day01
JUC-day01 什么是JUC线程的状态: wait sleep关键字:同步锁 原理(重点)Lock接口: ReentrantLock(可重入锁)—>AQS CAS线程之间的通讯 1 什么是JUC 1.1 JUC简介 在Java中,线程部分是一个重点,本篇文章说的JUC也是关于线程的。JUC就是java.util .con…...
Mind+Python+Mediapipe项目——AI健身之跳绳
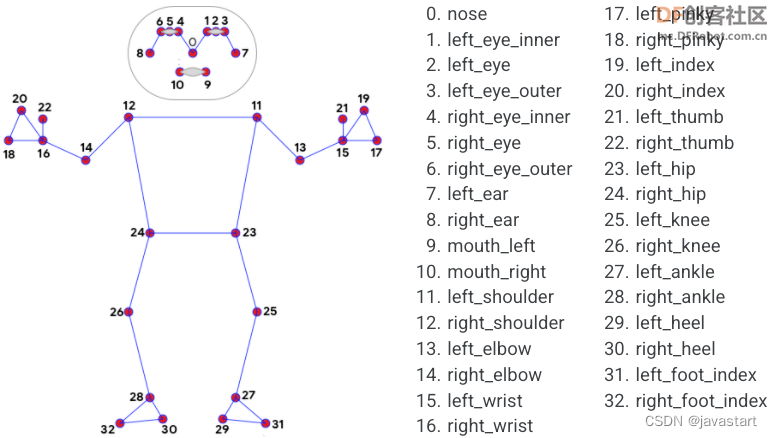
原文:MindPythonMediapipe项目——AI健身之跳绳 - DF创客社区 - 分享创造的喜悦 【项目背景】跳绳是一个很好的健身项目,为了获知所跳个数,有的跳绳上会有计数器。但这也只能跳完这后看到,能不能在跳的过程中就能看到,…...

数据库概述
20世纪60年代后期,就出现了数据库技术。取得成就如下:造就了四位图灵奖得主发展成为以数据建模和DBMS核心技术为主,内容丰富的一门学科。带动了一个巨大的软件产业-DBMS产品及其相关工具和解决方案。四个基本概念数据数据是数据库中存储的基本…...
【已解决】解决IDEA的maven刷新依赖时出现Connot reconnect错误
前言 小编我将用CSDN记录软件开发求学之路上亲身所得与所学的心得与知识,有兴趣的小伙伴可以关注一下!也许一个人独行,可以走的很快,但是一群人结伴而行,才能走的更远!让我们在成长的道路上互相学习&#…...
文件的变编译和引用、执行)
动态链接库(.so)文件的变编译和引用、执行
动态链接库(.so)文件的变编译和引用 动态链接库:SO(Shared Object)是一种动态链接库,也被称为共享库。它是一种可被多个程序共享使用的二进制代码库,其中包含已编译的函数和代码。与静态链接库不同,动态链接…...
文件解压命令)
linux(centos8)文件解压命令
linux解压命令tar 解压命令常用解压命令1 [.tar] 文件 解压到当前文件夹2 [.tar.gz] 文件 解压到当前文件夹3 [.tar] 解压到指定文件夹 -C 必须是大写unzip 解压命令常用解压命令1 [.zip]解压到当前文件夹2 [.zip] 解压到指定文件夹2 [.zip] 解压到指定文件夹(强行覆…...

阅读笔记6——通道混洗
一、逐点卷积 当前先进的轻量化网络大都使用深度可分离卷积或组卷积,以降低网络的计算量,但这两种操作都无法改变特征图的通道数,因此需要使用11的卷积。总体来说,逐点的11卷积有如下两点特性: 可以促进通道之间的信息…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...
