【leetcode 力扣刷题】栈—波兰式///逆波兰式相关知识和题目
波兰式、逆波兰式相关知识和题目
- 波兰式、逆波兰式介绍
- 常规表达式转换成逆波兰式
- ==编程让常规表达式转换成逆波兰式==
- 逆波兰式运算过程
- 常规表达式转换成波兰式
- ==编程让常规表达式转换成波兰式==
- 波兰式运算过程
- 150. 逆波兰式表达式求值
- 224. 基本计算器
- 227. 基本计算器Ⅱ
- 282. 给表达式添加运算符
波兰式、逆波兰式介绍
我们常看到的四则运算的计算式,比如2+3*(4-9),称为中缀表达式,人类去计算的时候知道这些运算符是有优先级的:()> */ > +-,但是让计算机去运算就有歧义了。上面的式子是很简单的,实际可以遇到很多层括号,计算机不会去括号的。因此就有了波兰式和逆波兰式。
波兰式和逆波兰式里,没有括号,计算没有歧义。
波兰式,也称为前缀表达式,即运算符在前面,数字在后面,上面的计算式转换成波兰式后为+2*3-49。
逆波兰式,也称为后缀表达式,即运算符都在后面,数字在前面,上面的计算式转换成逆波兰式后为2349-*+。
常规表达式转换成逆波兰式
可以通过添括号、开括号把中缀表达式变成逆波兰式,依旧以上面的式子为例子,添括号是指对应每个运算数和每次运算都添加一层括号,上式添括号后变成((2) + ((3) * ((4) - (9))))。然后从最里面一层括号开始,去括号,并将运算符放在数字后面:
- 1、((2) + ((3) * (49-)))
- 2、((2) + (349-*))
- 3、(2349-*+)
- 4、2349-*+
编程让常规表达式转换成逆波兰式
如何让计算机将中缀表达式变成逆波兰式呢? 转换成逆波兰式最重要的是运算符的顺序,需要考虑括号、优先级、以及左右顺序。转换过程中用一个栈保存遍历过程中遇到的运算符。从左到右遍历表达式的时候,遇到运算数,直接加入到结果表达式中;遇到运算符,需要入栈或者出栈:
- 如果当前运算符是’)‘,即括号内运算结束了,那么一直到栈内的’(',所有的运算符都出栈;
- 如果当前运算符是’(‘,表示括号内运算开始,’('直接入栈;
- 如果当前栈顶运算符是’(',当前运算符直接入栈;
- 如果当前运算符等级高于栈顶运算符等级,直接入栈;比如当前是’*‘,栈顶是’+',直接入栈;
- 如果当前运算符等级低于或者等于栈顶运算符等级,就出栈,直到栈空 or 栈顶运算等级更低,当前运算符入栈;
遍历完计算式后,如果栈不空将栈内运算符依次取出加入逆波兰式中,依旧以上面的2+3*(4-9)为例,转换成逆波兰式的过程如下:
| 原计算式 | 说 明 | 逆波兰式计算式 | ~栈~ |
|---|---|---|---|
| 2+3*(4-9) | 2—运算数直接加入结果中 | 2 | 空 |
| +3*(4-9) | +—运算符且栈空,直接入栈 | 2 | + |
| 3*(4-9) | 3—运算数直接加入结果中 | 23 | + |
| *(4-9) | *—运算符且比栈顶+等级高,直接入栈 | 23 | +* |
| (4-9) | (—直接入栈 | 23 | +*( |
| 4-9) | 4—运算数直接加入结果中 | 234 | +*( |
| -9) | - —运算符,且栈顶是(,直接入栈 | 234 | +*(- |
| 9) | 9—运算数直接加入结果中 | 2349 | +*(- |
| ) | )—运算符,前面到(都出栈加入结果中 | 2349- | +* |
| 将栈内运算符全都加入结果中 | 2349-*+ | 空 |
代码(C++)【不确定是否正确……】:
//判断优先级
int operator_priority(char ch){ if (ch== '+' || ch == '-')return 1;if (ch == '*' || ch == '/')return 2;if(ch == '(')return 0;return 0;
}
//判断是否是操作符
bool is_operator(char ch){return (ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '(' || ch == ')');
}//转换成逆波兰式
vector<string> RPN(string s){vector<string> tokens;string operators;for(int i = 0 ; i < s.size() ; ){//操作符if(is_operator(s[i])){//如果是) 直到遇到( 操作符一直出栈if(s[i] == ')'){while(operators.back()!='('){tokens.emplace_back(string(1,operators.back()));operators.pop_back();}operators.pop_back();i++;}//操作符栈为空 或者 栈顶为( 或者 当前为( 直接入栈else if(operators.empty() || operators.back() == '(' ||s[i] == '(')operators.push_back(s[i++]);//当前操作符优先级更高 直接入栈else if(operator_priority(s[i]) > operator_priority(operators.back()))operators.push_back(s[i++]);//当前操作符优先级更低或者一样 前面的出栈 else{do{tokens.emplace_back(string(1,operators.back()));operators.pop_back();}while(operator_priority(s[i]) <= operator_priority(operators.back()));operators.push_back(s[i++]);}} //操作数 else {int start = i;do{i++;}while(i<s.size() && !is_operator(s[i]));//操作数可能不止一位tokens.emplace_back(s.substr(start,i - start));}}while(!operators.empty()){tokens.emplace_back(string(1,operators.back()));operators.pop_back(); }return tokens;
}
逆波兰式运算过程
计算逆波兰式的时候,从前往后遍历式子,遇到运算符的时候,对其前面紧跟的两个运算数进行运算:
- 2349-*+从前往后遍历先遇到’-',然后计算得到23(-5)*+;
- 23(-5)*+继续往后遍历遇到’*',计算得到2(-15)+;
- 2(-15)+继续往后遍历遇到’+',计算得到-13即为答案;
常规表达式转换成波兰式
可以通过添括号、开括号把中缀表达式变成波兰式,依旧以上面的式子为例子,添括号是指对应每个运算数和每次运算都添加一层括号,上式添括号后变成((2) + ((3) * ((4) - (9))))。然后从最里面一层括号开始,去括号,并将运算符放在数字前面:
- 1、((2) + ((3) * (-49)))
- 2、((2) + (*3-49))
- 3、(+2*3-49)
- 4、+2*3-49
编程让常规表达式转换成波兰式
!!!还不会!!!待解决……
或许是按照逆波兰式的解法,只是从后向前遍历原计算式,最后得到的结果再reverse一下(?)
波兰式运算过程
计算波兰式的时候,从后往前,遇到运算符的时候,对其后面紧跟的两个运算数进行运算:
- +2*3-49从后往前最先遇到’-',运算后变成+2*3(-5)
- +2*3(-5)继续向前遍历遇到’*',运算后变成+2(-15)
- +2(-15)继续向前遍历遇到’+',运算后得到-13,即为答案
150. 逆波兰式表达式求值
题目链接:150. 逆波兰式表达式求值
题目内容:

实际就按照逆波兰式的计算方法,遍历逆波兰式,遇到运算数就放入栈,遇到运算符就依次取栈顶元素,取两次,得到运算数num1和num2,做运算后将结果压入栈中;直到遍历完逆波兰式,得到的就是结果。
需要注意,num1和num2的四则运算,加法和乘法,两个数可以交换左右顺序,但是在减法和除法中,num1 - num2 ≠ num2 - num1,需要注意第一个从栈顶取出的是num2,之后取的是num1。
代码如下(C++):
class Solution {
public:int evalRPN(vector<string>& tokens) {stack<int> num;for(int i = 0; i < tokens.size(); i++){//运算数直接入栈if(tokens[i] != "+" && tokens[i] != "-" && tokens[i] != "*" && tokens[i] != "/"){//需要将string转换成int数字num.push(atoi(tokens[i].c_str()));}else{//注意先取的是nums2int num2 = num.top();num.pop();//之后取的是nums1int num1 = num.top();num.pop();//根据运算符做运算switch(tokens[i][0]){case '+':num.push(num1 + num2);break;case '-':num.push(num1 - num2);break;case '*':num.push(num1 * num2);break;case '/': num.push(num1 / num2);break;}}}//最后压入栈的就是答案return num.top();}
};
224. 基本计算器
题目链接:224. 基本计算器
题目内容:

提示里需要注意的是,这个题目的运算只有加减,没有乘除。在只有加减的情况下,这个题目就单纯考察怎么开括号了。加法和减法优先级是一样的,括号对加法是没有用的,即(2+3) + (5-2)实际(5-2)的括号不加也行——(2+3) +5 -2;但对于减号却不行,(2+3) - (5-2),如果要去掉括号,就变成了(2+3) -5 +2,括号前面的减号,打开括号后,括号内+ 会变成-,-会变成+。并且这个效应会随着括号以及减号的累加而累加,比如-(…-(…-()…)…)这样的三重括号,第一层括号内符号全部要变,乘-1;第二层括号内又要全部乘-1,由于第一层括号已经乘了-1了,最终第二层括号内的就负负得正;最内层括号外面有三个-,因此最终还是会乘-1。
因此本题的重点在于开括号的时候,记录括号前面是+还是-,是+正常运算,是-就需要乘以-1。
实现代码(C++):
class Solution {
public:int calculate(string s) {int sign = 1;stack<int> ops;//记录括号前的符号,1表示加,-1表示减ops.push(1);int ans = 0;int i = 0, n = s.size();//遍历字符串swhile(i < n){if(s[i] == ' '){i++;}//如果是加号,紧接着的运算数是+还是-,需要看该层括号外对应的符号opselse if(s[i] == '+'){sign = ops.top();i++;}//如果是减号,后面数字的运算是+ or -,取决于括号前面的ops,且要反号else if(s[i] == '-'){sign = -ops.top();i++;}//如果是左括号,表示遇到新的一层括号,当前的sign即为这个括号前的符号,入栈else if(s[i] == '('){ops.push(sign);i++;}//如果是右括号,表示一层括号结束,pop掉对应的符号else if(s[i] == ')'){ops.pop();i++;}//是数字,就做相应的运算else{long num = 0;while(i < n && s[i] >= '0' && s[i] <= '9'){num = num*10 + s[i] - '0';i++;}ans += sign * num; //需要乘以sign,sign决定了这个数是加法还是减法}}return ans;}
};
如果题目中还有乘法除法,以及括号表示不同的优先级,可以将表达式转换成前缀表达式或者后缀表达式,即波兰式或者逆波兰式,然后开始运算。
227. 基本计算器Ⅱ
题目链接:227. 基本计算器Ⅱ
题目内容:

这个题目没有括号!只需要考虑加减乘除的优先级。因为乘法和除法优先级更高,在整个算式中应该先去计算乘法和除法,那我们就这么做!遍历字符串s的时候做如下操作:
- 如果是运算符,就记录该运算符【等到取到了其紧跟的数字,对其进行相应运算】;
- 如果是数字,那么就找到这个数字的终点,得到一个数字;
- 这个数字要做何操作,取决于前面的操作符,如果是乘or除,就用前面一个数与这个数字做相应运算,结果保存;
- 如果是加法,直接保存这个数;如果是减法,保存这个数的负数;
因为整个算式,第一个数字前如果有负号,那就保存其负数;如果第一个数是正数呢?因此我们要先给第一个数字一个初始化的操作符号’+'。 另外要注意遇到空格直接跳过。
最终将保存的数字全部都加起来即可。因为在遍历s的过程中已经先做了乘除以及减法了,最后统一做加法。
代码如下(C++):
class Solution {
public: int calculate(string s) {int idx = 0, n = s.size();//用于存算式中的数字vector<int> nums;//num用于计算s中的每个不止一位的数字,比如321,需要先遍历到3然后是2然后是1long num = 0;//保存每个数字前面的操作符char opt = '+';//遍历swhile(idx < n){//如果是空格直接跳过if(s[idx] == ' '){idx++;continue;}//如果是数字if(s[idx] >= '0' && s[idx] <= '9'){//计算这个数字num = 0;do{num = num*10 + s[idx] -'0';idx++;}while(idx<n && s[idx] >= '0' && s[idx] <= '9');//根据这个数字前面的操作符来保存switch(opt){case '+': nums.emplace_back(num);break;case '-': nums.emplace_back(-num);break;case '*': nums.back() *= num;break;case '/': nums.back() /= num;break;}}//操作符else{opt = s[idx];idx++;}}num = 0;//将保存的数都加起来得到结果for(int i = 0; i < nums.size(); i++)num += nums[i];return num;}
};
282. 给表达式添加运算符
题目链接:282. 给表达式添加运算符
题目内容:

这个题目我是完全不会做……看的题解,然后试图理解……再自己试着写一写代码和题解。
题目里说在数字之间添加运算符,实际上可以添加也可以不添加,因此针对每两个数字之间的位置,有4种选择——不添加,或者添加+、-、*中的一个。此题用回溯法解题,时间复杂度是O(4^n)。
用回溯法解题的思路如下:
- 对于每两个数字之间不添加or添加以及添加什么,有四种选择:
- 什么都不添加:更新之前表达式的最后一个数字num1,假设当前数字是num2,num1=num1*10+num2,同时更新之前的表达式结果val = val - num1(旧) + num1(新)。
- 添加一个’+':更新之前表达式,加上当前的数字num2,表达式的值val = val + num2;
- 添加一个’-':更新之前表达式,减去当前的数字num2,表达式的值val = val - num2;
- 添加一个’*‘:更新之前表达式,同时注意’*‘优先级更高,表达式最后一个数num1,不管这个数之前是’+‘还是减’-‘还是乘’*',表达式的值先减去val,再加上num1*num2;
- 进行深度搜索的结束条件是,遍历完字符串的时候,如果val == target就将当前的表达式加入结果数组中;
- 由于每一步更新表达式值的时候,可能涉及到上一步表达式的最后一个数字的操作,因此在递归调用函数的时候需要将num1传递下去;表达式要一直增加,因此要传递表达式;表达式的值也需要更新,因此要传递val;添加什么操作符也需要传递。
代码如下(C++)——抄的官方题解,真不会啊………………啊啊啊啊:
class Solution {
public:vector<string> addOperators(string num, int target) {int n = num.length();vector<string> ans;function<void(string&, int, long, long)> backtrack = [&](string &expr, int i, long res, long mul) {if (i == n) {if (res == target) {ans.emplace_back(expr);}return;}int signIndex = expr.size();if (i > 0) {expr.push_back(0); // 占位,下面填充符号}long val = 0;// 枚举截取的数字长度(取多少位),注意数字可以是单个 0 但不能有前导零for (int j = i; j < n && (j == i || num[i] != '0'); ++j) {val = val * 10 + num[j] - '0';expr.push_back(num[j]);if (i == 0) { // 表达式开头不能添加符号backtrack(expr, j + 1, val, val);} else { // 枚举符号expr[signIndex] = '+'; backtrack(expr, j + 1, res + val, val);expr[signIndex] = '-'; backtrack(expr, j + 1, res - val, -val);expr[signIndex] = '*'; backtrack(expr, j + 1, res - mul + mul * val, mul * val);}}expr.resize(signIndex);};string expr;backtrack(expr, 0, 0, 0);return ans;}
};
相关文章:

【leetcode 力扣刷题】栈—波兰式///逆波兰式相关知识和题目
波兰式、逆波兰式相关知识和题目 波兰式、逆波兰式介绍常规表达式转换成逆波兰式编程让常规表达式转换成逆波兰式逆波兰式运算过程常规表达式转换成波兰式编程让常规表达式转换成波兰式波兰式运算过程 150. 逆波兰式表达式求值224. 基本计算器227. 基本计算器Ⅱ282. 给表达式添…...
Web 第一步:HTTP 协议(基础)
这里是JavaWeb的开头部分!那么先解释一下吧: Web:全球广域网,也称为万维网(www),能够通过浏览器访问的网站。 JavaWeb:是用Java技术来解决相关 Web 互联网领域的技术栈。 …...

【Vue】快速入门案例与工作流程的讲解
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟在这里,我要推荐给大家我的专栏《Vue快速入门》。…...
--camera - codec - 多媒体-编解码)
LuatOS-SOC接口文档(air780E)--camera - codec - 多媒体-编解码
常量 常量 类型 解释 codec.MP3 number MP3格式 codec.WAV number WAV格式 codec.AMR number AMR-NB格式,一般意义上的AMR codec.AMR_WB number AMR-WB格式 codec.create(type, isDecoder) 创建编解码用的codec 参数 传入值类型 解释 int 多媒…...

《动手学深度学习 Pytorch版》 6.6 卷积神经网络
import torch from torch import nn from d2l import torch as d2l6.6.1 LeNet LetNet-5 由两个部分组成: - 卷积编码器:由两个卷积核组成。 - 全连接层稠密块:由三个全连接层组成。模型结构如下流程图(每个卷积块由一个卷积层、…...
【微信小程序】项目初始化
| var() CSS 函数可以插入一个自定义属性(有时也被称为“CSS 变量”)的值,用来代替非自定义 属性中值的任何部分。 1.初始化样式与颜色 view,text{box-sizing: border-box; } page{--themColor:#ad905c;--globalColor:#18191b;--focusColor…...
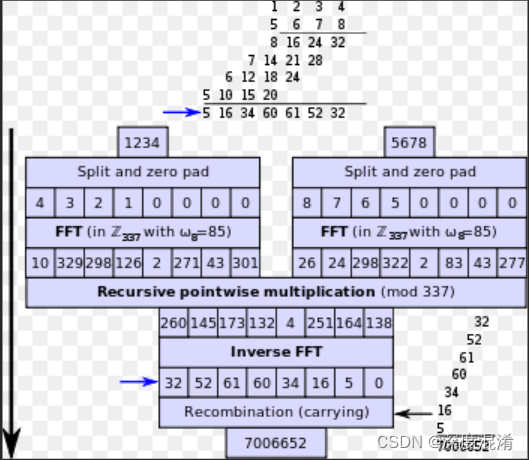
C#,《小白学程序》第二十六课:大数乘法(BigInteger Multiply)的Toom-Cook 3算法及源程序
凑数的,仅供参考。 1 文本格式 /// <summary> /// 《小白学程序》第二十六课:大数(BigInteger)的Toom-Cook 3乘法 /// Toom-Cook 3-Way Multiplication /// </summary> /// <param name"a"></par…...
destoon自定义一个archiver内容文档
在archiver目录建立以下代码: <?php define(DT_REWRITE, true); require ../common.inc.php; $EXT[archiver_enable] or dheader(DT_PATH); //$DT_BOT or dheader(DT_PATH); $N $M $T array(); $mid or $mid 5; $vmid $list 0; foreach($MODULE as $k>…...
5-1 Dataset和DataLoader
Pytorch通常使用Dataset和DataLoader这两个工具类来构建数据管道。 Dataset定义了数据集的内容,它相当于一个类似列表的数据结构,具有确定的长度,能够用索引获取数据集中的元素。 而DataLoader定义了按batch加载数据集的方法,它是…...
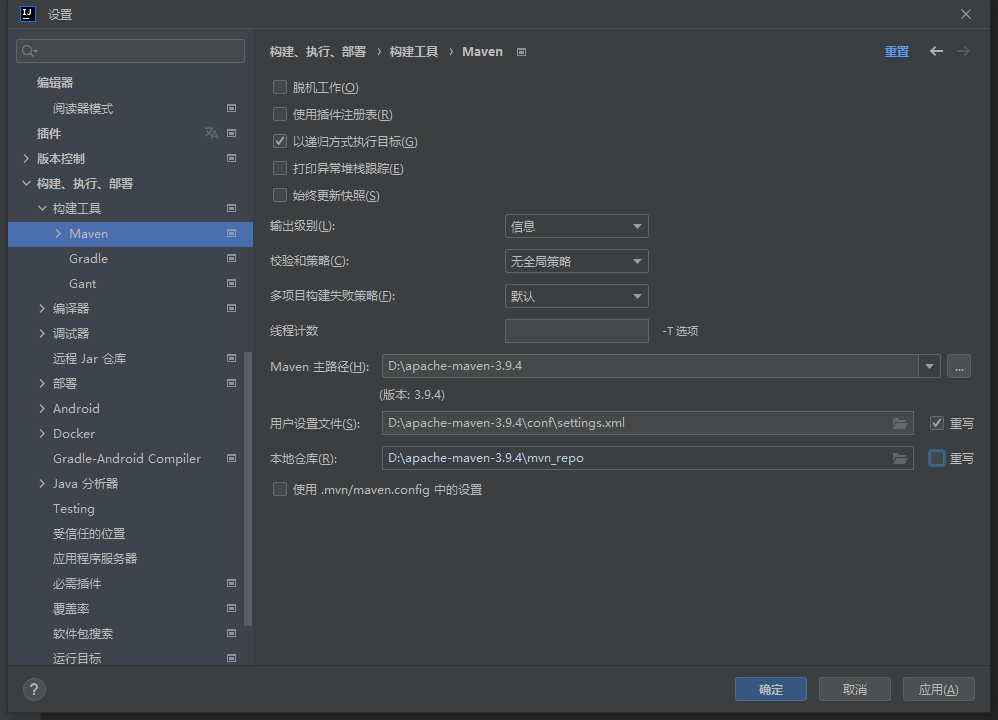
IDEA创建完Maven工程后,右下角一直显示正在下载Maven插件
原因: 这是由于新建的Maven工程,IDEA会用它内置的默认的Maven版本,使用国外的网站下载Maven所需的插件,速度很慢 。 解决方式: 每次创建 Project 后都需要设置 Maven 家目录位置(就是我们自己下载的Mav…...

最新清理删除Mac电脑内存空间方法教程
Mac电脑使用的时间越久,系统的运行就会变的越卡顿,这是Mac os会出现的正常现象,卡顿的原因主要是系统缓存文件占用了较多的磁盘空间,或者Mac的内存空间已满。如果你的Mac运行速度变慢,很有可能是因为磁盘内存被过度占用…...

【调试经验】MySQL - fatal error: mysql/mysql.h: 没有那个文件或目录
机器环境: Ubuntu 22.04.3 LTS 报错问题 在编译一个项目时出现了一段SQL报错: CGImysql/sql_connection_pool.cpp:1:10: fatal error: mysql/mysql.h: 没有那个文件或目录 1 | #include <mysql/mysql.h> | ^~~~~~~~~~~~~~~ c…...

腾讯mini项目-【指标监控服务重构】2023-08-12
今日已办 Watermill Handler 将 4 个阶段的逻辑处理定义为 Handler 测试发现,添加的 handler 会被覆盖掉,故考虑添加为 middleware 且 4 个阶段的处理逻辑针对不同 topic 是相同的。 参考https://watermill.io/docs/messages-router/实现不同topic&am…...

kubeadm部署k8sv1.24使用cri-docker做为CRI
目的 测试使用cri-docker做为containerd和docker的中间层垫片。 规划 IP系统主机名10.0.6.5ubuntu 22.04.3 jammymaster01.kktb.org10.0.6.6ubuntu 22.04.3 jammymaster02.kktb.org10.0.6.7ubuntu 22.04.3 jammymaster03.kktb.org 配置 步骤: 系统优化 禁用sw…...
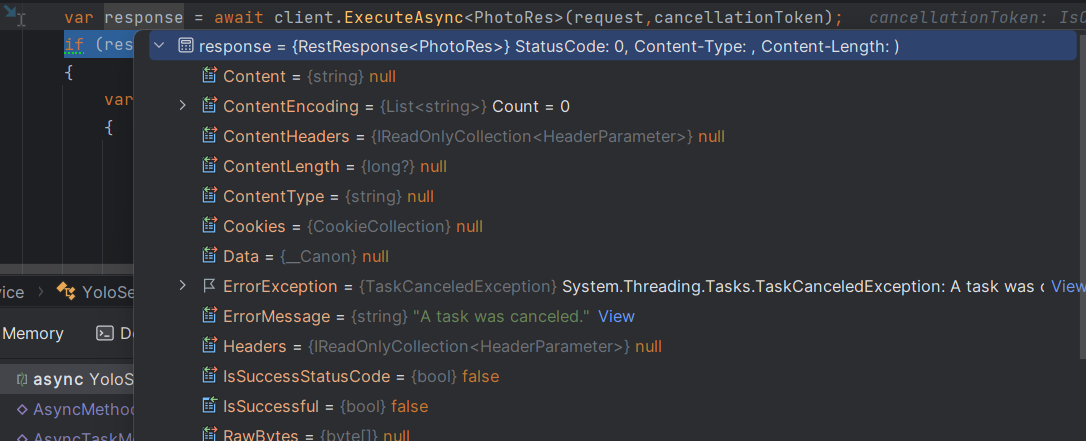
在c#中使用CancellationToken取消任务
目录 🚀介绍: 🐤简单举例 🚀IsCancellationRequested 🚀ThrowIfCancellationRequested 🐤在控制器中使用 🚀通过异步方法的参数使用cancellationToken 🚀api结合ThrowIfCancel…...
【项目经验】:elementui多选表格默认选中
一.需求 在页面刚打开就默认选中指定项。 二.方法Table Methods toggleRowSelection用于多选表格,切换某一行的选中状态,如果使用了第二个参数,则是设置这一行选中与否(selected 为 true 则选中)row, selected 详细…...

外星人入侵游戏-(创新版)
🌈write in front🌈 🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...
HTML 学习笔记(基础)
它是超文本标记语言,由一大堆约定俗成的标签组成,而其标签里一般又有一些属性值可以设置。 W3C标准:网页主要三大部分 结构:HTML表现:CSS行为:JavaScript <!DOCTYPE html> <html lang"zh-…...

最小二乘法
Least Square Method 1、相关的矩阵公式2、线性回归3、最小二乘法3.1、损失函数(Loss Function)3.2、多维空间的损失函数3.3、解析法求解3.4、梯度下降法求解 1、相关的矩阵公式 P r e c o n d i t i o n : ξ ∈ R n , A ∈ R n ∗ n i : σ A ξ σ ξ…...

使用stelnet进行安全的远程管理
1. telnet有哪些不足? 2.ssh如何保证数据传输安全? 需求:远程telnet管理设备 用户定义需要在AAA模式下: 开启远程登录的服务:定义vty接口 然后从R2登录:是可以登录的 同理R3登录: 在R1也可以查…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
