二维凸包(Graham) 模板 + 详解
(闲话)
上了大学后没怎么搞oi,从土木跑路到通信了(提桶开润大成功!),但是一年上两年的课(补的),保研也寄掉了(
说起来自从博客被大学同学发现并在我面前一个一个字读了以后,我:这谁写的,太他ma二次元了,本人决定以后就用比较正常的表述来写这些了(
最近在裸打acm,然后因为只会数据结构派不上用场被队友叫去整点其他部分内容,这两天随便摸了个凸包,整理一下Graham算法,例题还是洛谷的,顺便丢上自己的代码解释步骤:
一、找最低点(y值为min)做起始点root
root必在凸包上就在读入的时候顺便处理掉就行了。为了能顺利找到,root先赋一个大于所有y的值即可。如果出现最低点有很多个,记得一定要找x值最小/最大的点,不然遇到hack数据就没了(原因存疑,个人猜想保留)
for (int a = 1 ; a <= n ; ++ a) {scanf("%lf%lf",&s[a].x,&s[a].y);if (s[a].y < s[root].y || (s[a].y == s[root].y && s[a].x < s[root].x)) root = a;
} //.x的地方换成大于号也可此处的s是定义的结构体point,顾名思义。其中的v是存的斜率。这玩意儿干啥用的之后再说
struct point {double x,y,v;
};二、Grahamの排序
排序是精髓。Graham用的排序是以root点为基准,按照其他点和它连线的斜率来决定先扫哪个点再扫哪个点的,这样优势很明显,我意会了一下就记住了,具体原理没找,就不讲了,记得按照斜率扫就行了(
所以,我们要根据这个斜率对原来的一堆点进行排序。我用的是atan2,当然自己算角也行,就是麻烦点。根据下列引用可以得知,atan2如果将点集排序成从右往左扫,它的值是从0升到π,这个值用上文中的结构体point里的v存着。排序的时候cmp按照.v排序就行了。

顺便说一声,直接排的话,遇到斜率相同的点会乱序,遇到hack数据就寄了,所以排序是按照先排斜率再排比较的两点各自与root的距离。
Graham按极角排序但不用距离作为第二关键字会错的原因
/*先按照斜率.v进行比较,再按照距离进行比较*/
bool cmp(point x,point y) {return x.v == y.v ? dis(x,s[1]) < dis(y,s[1]) : x.v < y.v;
}sort(s + 2,s + n + 1,cmp); //第一个点是root,不用排
那排序就很简单地完成了
三、扫描搜点构成凸包
接下来就是对排序的点遍历,开始包了。我们每次加的点都要满足能构成“当前的凸包”,我是从右往左扫的,所以。。不对,在这之前先介绍二维的叉积吧
就是这么个玩意儿:A.x * B.y - B.x * A.y,AB为俩向量
如果叉出来的结果为正,说明A正旋到B<180°;结果为负,说明A正旋到B>180°。正旋就是从x正向往y正向那方向转
咱以从右往左扫为例,我们要整的凸包此时新的一段一定是要更“往左边拐的”,就是新的凸包边应该是上一个凸包边正旋小于180°能得到的
于是我们把已经构成的凸包的最新的一段,和将要连上的一段整成两个向量(都是从先构造到的点指向后构造的点),叉一下,如果结果为负或0,就说明我们新的边“往右拐”了,这样上一次的凸包的电就不在新的凸包边集上了。而且此时有可能再上一次的边也不满足要求,就还得倒回去接着叉(此时构造向量时,要将之前排除的点的相关部分给换成当前判断的点)。大概是这个样子:
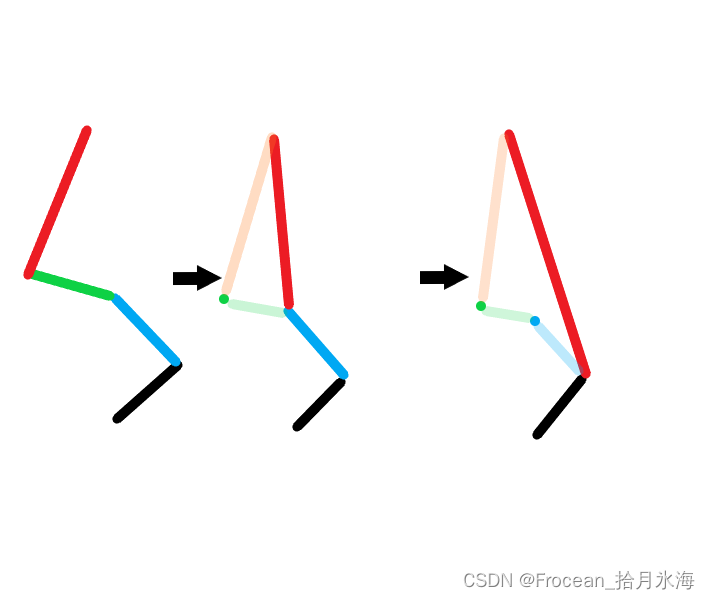
这判断就是jud函数里面的return那部分。为了防止栈被掏空,溯源到root就不继续判断了。
具体代码部分见下:
bool jud(point a,point b,point c,point d) {double ix = b.x - a.x,iy = b.y - a.y;double jx = d.x - c.x,jy = d.y - c.y;return (ix * jy - iy * jx) <= 0;
} //我把向量构成搬到里面来了,小于等于0即判断向量正旋类型for (int a = 2 ; a <= n ; ++ a) {while (tot > 1 && jud(已处理点构成的向量,新处理点构成的向量) --tot;que[++tot] = s[a];}que即为存凸包上的点的栈
四、Blabla
总之这样凸包就已经求出来了,根据题目要求算出要算的东西就行了。 放下上文例题代码:
#include <algorithm>
#include <cstdio>
#include <cmath>
#define N 100010
using namespace std;
struct point {double x,y,v;
} s[N],que[N << 1];
double ans = 0;
int n,root = 0,tot = 0;
void swap(point &x,point &y) {point z = x; x = y,y = z;}
double pf(double x) {return x * x;} //平方
double dis(point i,point j) {return sqrt(pf(i.x - j.x) + pf(i.y - j.y));} //求两点距离
bool cmp(point x,point y) {return x.v == y.v ? dis(x,s[1]) < dis(y,s[1]) : x.v < y.v;}
bool jud(point a,point b,point c,point d) {double ix = b.x - a.x,iy = b.y - a.y;double jx = d.x - c.x,jy = d.y - c.y;return (ix * jy - iy * jx) <= 0; //判断正旋角度是否满足题意
}
int main() {s[0].x = 1e6 + 1;s[0].y = 1e6 + 1;scanf("%d",&n);for (int a = 1 ; a <= n ; ++ a) { //读入点并确定root scanf("%lf%lf",&s[a].x,&s[a].y);if (s[a].y < s[root].y || (s[a].y == s[root].y && s[a].x < s[root].x)) root = a;}swap(s[1],s[root]);que[++tot] = s[1]; //root入栈for (int a = 2 ; a <= n ; ++ a) //计算每点与root的斜率 s[a].v = atan2(s[a].y - s[1].y,s[a].x - s[1].x);sort(s + 2,s + n + 1,cmp); //按斜率排序 for (int a = 2 ; a <= n ; ++ a) { //从右往左扫描 把点丢进凸包 再丢出来一些 while (tot > 1 && jud(que[tot - 1],que[tot],que[tot],s[a])) --tot;que[++tot] = s[a];}/*根据本题要求求出凸包周长*/que[++tot] = s[1];for (int a = 1 ; a < tot ; ++ a) ans += dis(que[a],que[a + 1]);printf("%.2lf\n",ans);return 0;
}相关文章:

二维凸包(Graham) 模板 + 详解
(闲话) 上了大学后没怎么搞oi,从土木跑路到通信了(提桶开润大成功!),但是一年上两年的课(补的),保研也寄掉了( 说起来自从博客被大学同学发现并…...
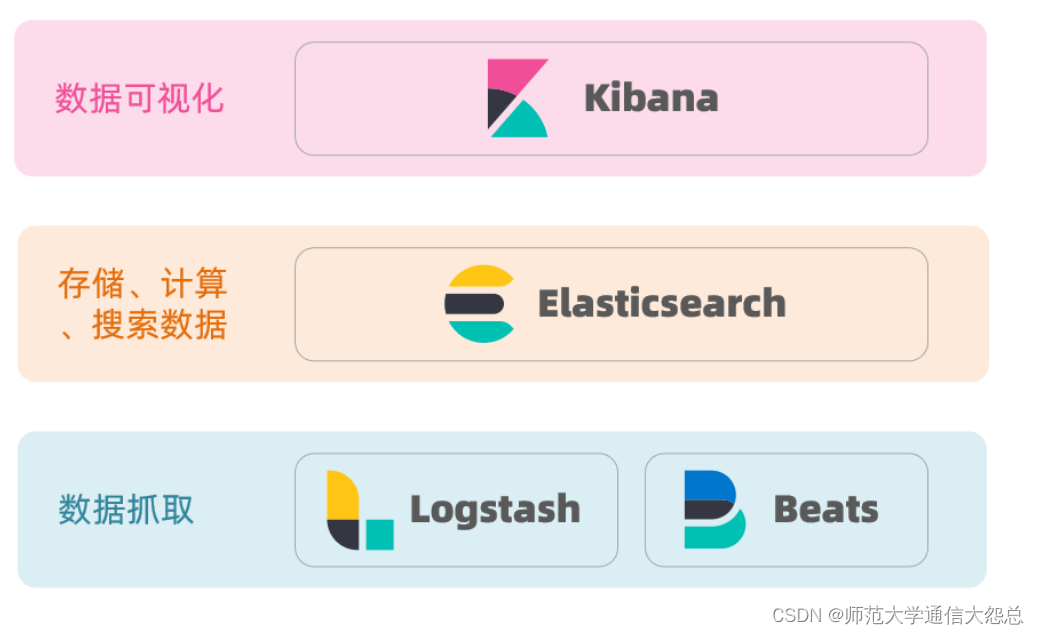
ElasticSearch(ES)简单介绍
ES简介 Elasticsearch(通常简称为ES)是一个开源的分布式搜索和分析引擎,旨在处理各种类型的数据,包括结构化、半结构化和非结构化数据。它最初是为全文搜索而设计的,但随着时间的推移,它已经演变成一个功能…...

OpenCV(三十五):凸包检测
1.凸包检测介绍 凸包检测是计算凸包的一种技术,凸包就是:给定二维平面上的点集,将最外层的点连接起来构成的凸边形,它是包含点集中所有的点。 2.凸包检测函数convexHull() void cv::convexHull ( InputArray points, OutputArra…...
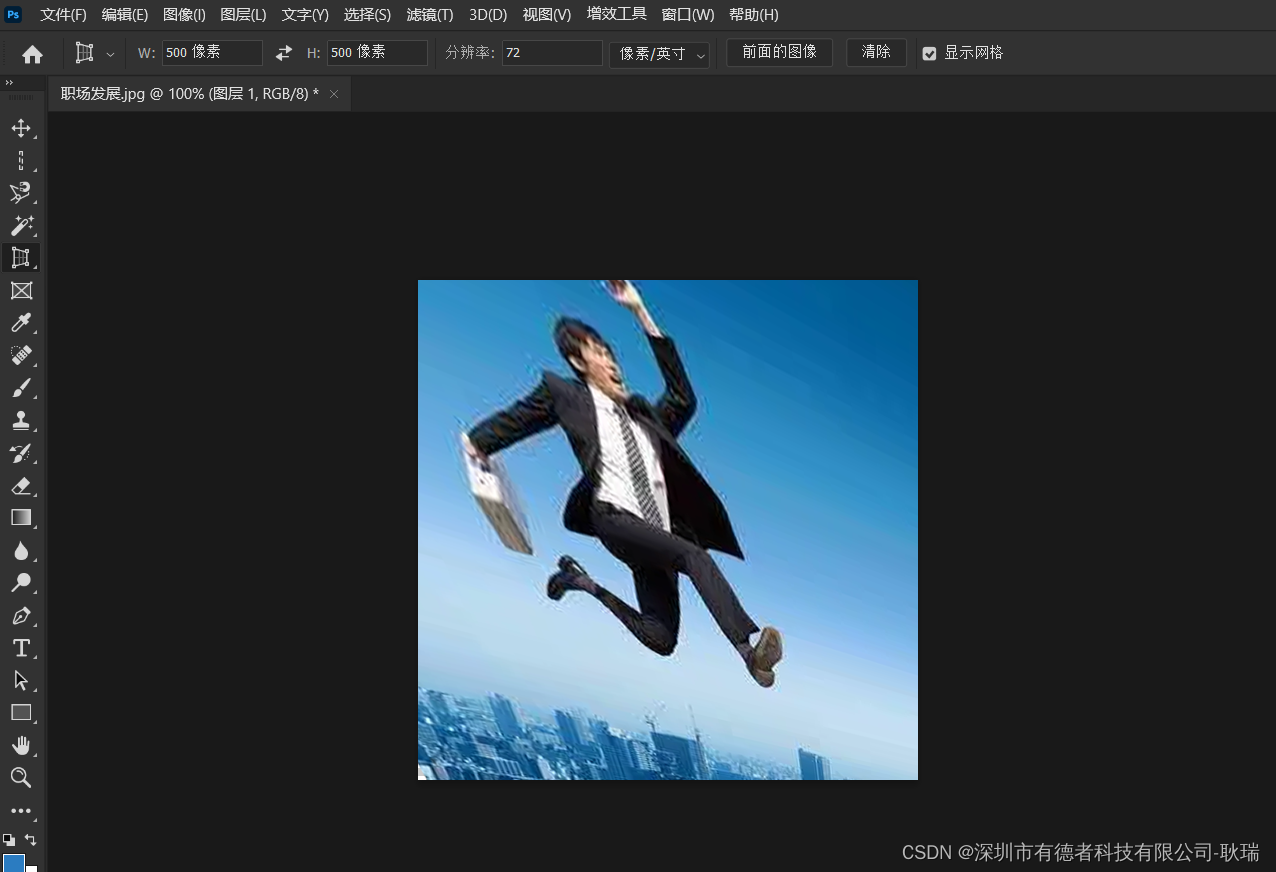
PS 透视裁剪工具
上文 PS 裁剪工具及工具栏配置讲解 我们讲完了裁剪工具 然后 我们继续来研究 透视裁剪工具 切换到 透视裁剪工具 后 我们先点击左上方的清除 先不要这些多的配置 然后 我们可以先用鼠标在图像上 画出一个局域 然后 我们去拖他四个角中的其中一个 就能拖出一些不同的形状 然…...
)
每日一个C库函数-#1-memset()
每日一个C库函数-#1-memset() 来源 C 标准库 - <string.h> 声明 void *memset(void *str, int c, size_t n);str:要填充的内存块;c:要被设置的值(以何值填充)。该值以 int 形式传递,填充内存块时…...

GraphQL基础知识与Spring for GraphQL使用教程
文章目录 1、数据类型1.1、标量类型1.2. 高级数据类型 基本操作2、Spring for GraphQL实例2.1、项目目录2.2、数据库表2.3、GraphQL的schema.graphql2.4、Java代码 3、运行效果3.1、添加用户3.2、添加日志3.3、查询所有日志3.4、查询指定用户日志3.5、数据订阅 4、总结 GraphQL…...
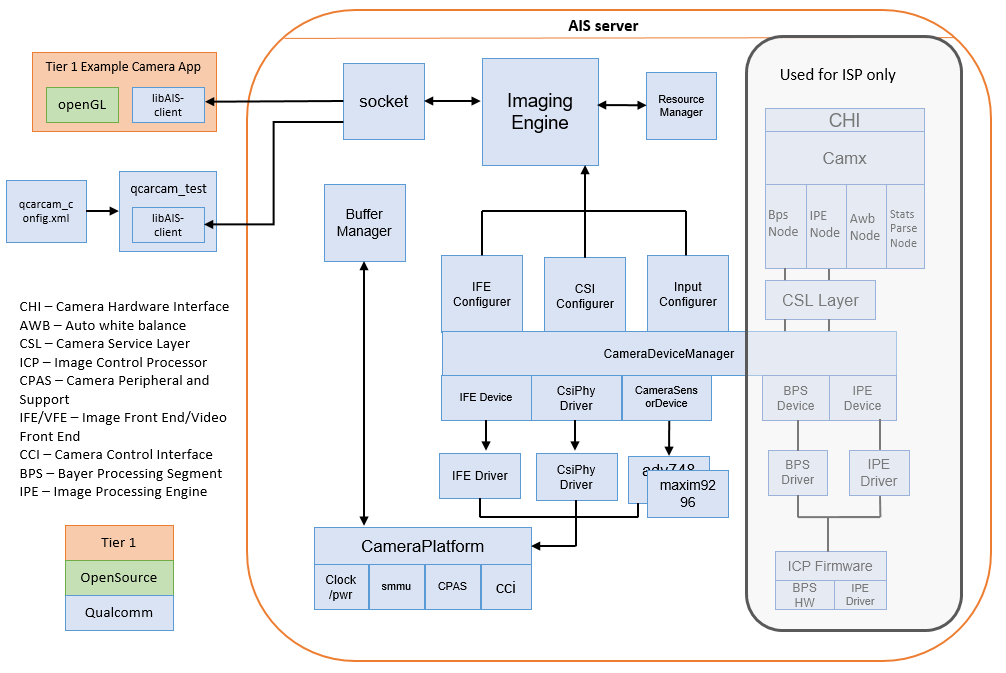
【SA8295P 源码分析】97 - QNX AIS Camera 框架介绍 及 Camera 工作流程分析
【SA8295P 源码分析】97 - QNX AIS Camera 框架介绍 及 Camera 工作流程分析 一、QNX AIS Server 框架分析二、QNX Hypervisor / Android GVM 方案介绍三、Camera APP 调用流程分析四、QCarCam 状态转换过程介绍五、Camera 加串-解串 硬件链路分析六、摄像头初始化检测过程介绍…...

威胁的数量、复杂程度和扩散程度不断上升
Integrity360 宣布了针对所面临的网络安全威胁、数量以及事件响应挑战的独立研究结果。 数据盗窃、网络钓鱼、勒索软件和 APT 是最令人担忧的问题 这项调查于 2023 年 8 月 9 日至 14 日期间对 205 名 IT 安全决策者进行了调查,强调了他们的主要网络安全威胁和担忧…...
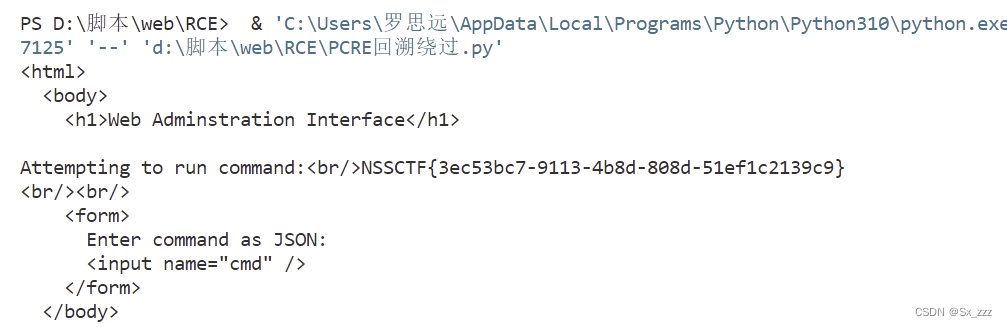
NSSCTF web 刷题记录2
文章目录 前言题目[广东强网杯 2021 团队组]love_Pokemon[NCTF 2018]Easy_Audit[安洵杯 2019]easy_web[NCTF 2018]全球最大交友网站prize_p2[羊城杯 2020]easyser[FBCTF 2019]rceservice方法一方法二 前言 今天是2023年9月13号,刷题记录2正式开始。时间来到九月十七…...

Linux驱动之INPUT子系统框架
目录 一、input 子系统简介 二、input 驱动编写流程 1、注册 input_dev 2、上报输入事件 三、input_event 结构体 按键、鼠标、键盘、触摸屏等都属于输入(input)设备, Linux 内核为此专门做了一个叫做 input子系统的框架来处理输入事件。输入设备本质上还是字符设…...

Long类型雪花算法ID返回前端后三位精度缺失问题解决
目录 一、问题描述二、问题复现1.Maven依赖2.application.yml 配置3.DemoController.java4.snowflakePage.html 页面5.DemoControllerAdvice.java 监听6.问题复现 三、原因分析四、问题解决方案一方案二 一、问题描述 Java 后端使用雪花算法生成 Long 类型的主键 ID࿰…...
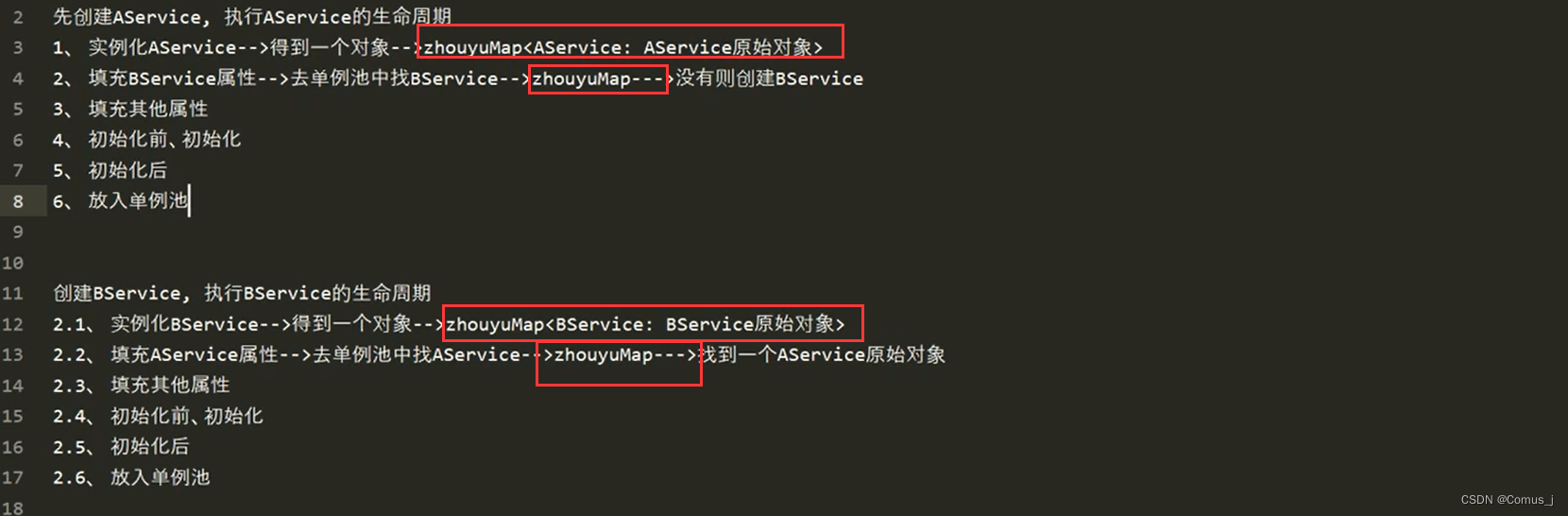
6.8-SpringIoC之循环依赖底层源码解析
解决靠,三级缓存 创建Map,存不完整的Bean 存在问题:属性存在但没有值...
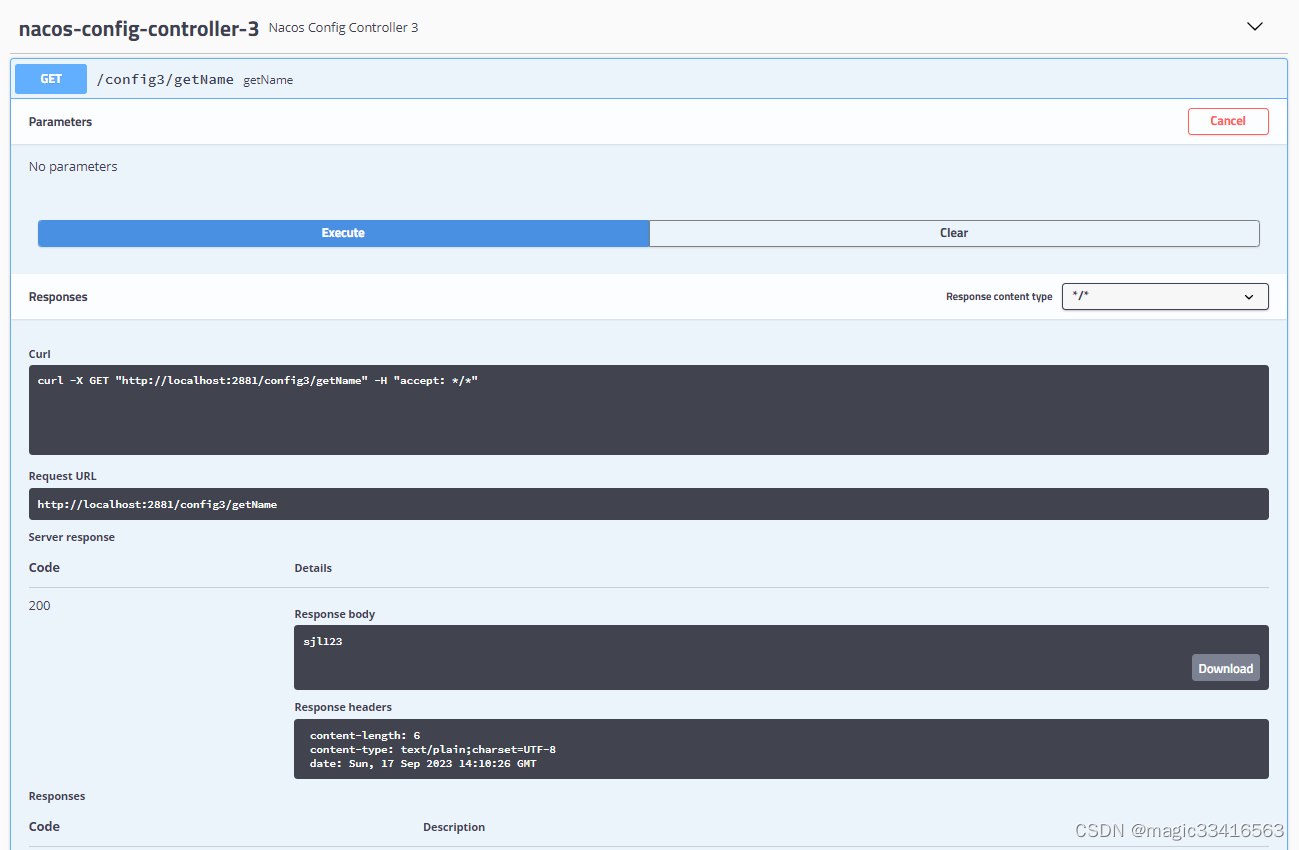
Springboot 实践(18)Nacos配置中心参数自动刷新测试
前文讲解了Nacos 2.2.3配置中心的服务端的下载安装,和springboot整合nacos的客户端。Springboot整合nacos关键在于使用的jar版本要匹配,文中使用版本如下: ☆ springboot版本: 2.1.5.RELEASE ☆ spring cloud版本 Greenwich.RELEASE ☆ sp…...

uniapp引入小程序原生插件
怎么在uniapp中使用微信小程序原生插件,以收钱吧支付插件为例 1、在manifest.json里的mp-weixin中增加插件配置 "mp-weixin" : {"appid" : "你的小程序appid","setting" : {"urlCheck" : false},"usingCom…...

自己记录微信小程序开发遇到的问题
在HBuilder X中【运行】--【小程序】--【运行设置】,小程序运行配置,将【微信开发者工具】的安装路径配置进去,首次运行会自动让你填写; 1、hbuildx运行到微信开发者工具报错 Error: Unbalanced delimiter found in string 错误…...

【leetcode 力扣刷题】栈—波兰式///逆波兰式相关知识和题目
波兰式、逆波兰式相关知识和题目 波兰式、逆波兰式介绍常规表达式转换成逆波兰式编程让常规表达式转换成逆波兰式逆波兰式运算过程常规表达式转换成波兰式编程让常规表达式转换成波兰式波兰式运算过程 150. 逆波兰式表达式求值224. 基本计算器227. 基本计算器Ⅱ282. 给表达式添…...
Web 第一步:HTTP 协议(基础)
这里是JavaWeb的开头部分!那么先解释一下吧: Web:全球广域网,也称为万维网(www),能够通过浏览器访问的网站。 JavaWeb:是用Java技术来解决相关 Web 互联网领域的技术栈。 …...

【Vue】快速入门案例与工作流程的讲解
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟在这里,我要推荐给大家我的专栏《Vue快速入门》。…...
--camera - codec - 多媒体-编解码)
LuatOS-SOC接口文档(air780E)--camera - codec - 多媒体-编解码
常量 常量 类型 解释 codec.MP3 number MP3格式 codec.WAV number WAV格式 codec.AMR number AMR-NB格式,一般意义上的AMR codec.AMR_WB number AMR-WB格式 codec.create(type, isDecoder) 创建编解码用的codec 参数 传入值类型 解释 int 多媒…...

《动手学深度学习 Pytorch版》 6.6 卷积神经网络
import torch from torch import nn from d2l import torch as d2l6.6.1 LeNet LetNet-5 由两个部分组成: - 卷积编码器:由两个卷积核组成。 - 全连接层稠密块:由三个全连接层组成。模型结构如下流程图(每个卷积块由一个卷积层、…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
