简单介绍神经网络中不同优化器的数学原理及使用特性【含规律总结】
当涉及到优化器时,我们通常是在解决一个参数优化问题,也就是寻找能够使损失函数最小化的一组参数。当我们在无脑用adam时,有没有斟酌过用这个是否合适,或者说凭经验能够有目的性换用不同的优化器?是否用其他的优化器可以更好的解决问题?那我就介绍解释几种常用的优化器的基本原理:
-
随机梯度下降(SGD):
SGD 是最基本的优化算法之一。它通过计算当前位置的梯度(即损失函数对参数的导数),然后朝着梯度的反方向更新参数。数学上可以表示为:
w = w − α ⋅ ∇ J ( w ) w=w−α⋅∇J(w) w=w−α⋅∇J(w)
其中, w w w 是待优化的参数, α \alpha α 是学习率, ∇ J ( w ) \nabla J(w) ∇J(w) 是损失函数关于参数的梯度。
-
动量优化器(Momentum):
Momentum 在 SGD 的基础上引入了动量项,它可以理解为模拟物体在空间中运动的物理量。这个动量项会考虑之前的更新,从而使更新方向在一定程度上保持一致。数学上可以表示为:
v = β ⋅ v + ( 1 − β ) ⋅ ∇ J ( w ) v=\beta⋅v+(1−\beta)⋅ \nabla J(w) v=β⋅v+(1−β)⋅∇J(w)
w = w − α ⋅ v w=w−α⋅v w=w−α⋅v
其中, v v v 是动量, β \beta β 是动量因子,控制之前更新的影响程度。
-
AdaGrad:
AdaGrad 是自适应学习率的一种算法。它会根据参数的历史梯度调整学习率,使得对于稀疏数据来说可以使用一个更大的学习率,而对于频繁出现的数据则会使用较小的学习率。数学上可以表示为:
w = w − α G + ϵ ⋅ ∇ J ( w ) w = w - \frac{\alpha}{\sqrt{G + \epsilon}} \cdot \nabla J(w) w=w−G+ϵα⋅∇J(w)
其中, G G G 是梯度的平方和的累积, ϵ \epsilon ϵ 是一个很小的数,防止除零错误。
-
RMSprop:
RMSprop 是 AdaGrad 的一个变体,它引入了一个衰减系数 β \beta β,用来控制历史梯度的权重。这使得 RMSprop 更加平滑地调整学习率。数学上可以表示为:
G = β ⋅ G + ( 1 − β ) ⋅ ( ∇ J ( w ) ) 2 G = \beta \cdot G + (1 - \beta) \cdot (\nabla J(w))^2 G=β⋅G+(1−β)⋅(∇J(w))2
w = w − α G + ϵ ⋅ ∇ J ( w ) w = w - \frac{\alpha}{\sqrt{G + \epsilon}} \cdot \nabla J(w) w=w−G+ϵα⋅∇J(w)
其中, G G G 是平方梯度的指数加权移动平均。
-
Adam:
Adam 结合了 Momentum 和 RMSprop 的特性,是一种同时考虑动量和自适应学习率的优化器。它可以动态地调整每个参数的学习率,并且可以保持更新方向的一致性。Adam 还引入了偏差修正,以解决初始训练时的偏差问题。数学上可以表示为:
m = β 1 ⋅ m + ( 1 − β 1 ) ⋅ ∇ J ( w ) m = \beta_1 \cdot m + (1 - \beta_1) \cdot \nabla J(w) m=β1⋅m+(1−β1)⋅∇J(w)
v = β 2 ⋅ v + ( 1 − β 2 ) ⋅ ( ∇ J ( w ) ) 2 v = \beta_2 \cdot v + (1 - \beta_2) \cdot (\nabla J(w))^2 v=β2⋅v+(1−β2)⋅(∇J(w))2
m ^ = m 1 − β 1 t \hat{m} = \frac{m}{1 - \beta_1^t} m^=1−β1tm
v ^ = v 1 − β 2 t \hat{v} = \frac{v}{1 - \beta_2^t} v^=1−β2tv
w = w − α v ^ + ϵ ⋅ m ^ w = w - \frac{\alpha}{\sqrt{\hat{v} + \epsilon}} \cdot \hat{m} w=w−v^+ϵα⋅m^
其中, m m m 和 v v v 分别是动量和平方梯度的移动平均, β 1 \beta_1 β1 和 β 2 \beta_2 β2 是衰减系数, t t t 是当前迭代次数, ϵ \epsilon ϵ 是避免除零错误的小数。
其实,每种优化器都有其适用的场景,具体的选择需要根据问题的特性和实际实验的结果来决定。
如果你真的对优化器的数学原理不感冒,只是一个最小白的神经网络构建者,那么我尝试总结几条,最浅显易懂的优化器特征,以供查阅:
-
随机梯度下降(SGD):这是最基本的优化算法之一,它在每个训练步骤中沿着梯度的反方向更新权重。它有时候可能需要更多的调参工作来获得好的性能。
-
动量优化器(Momentum):当需要考虑前一次梯度调整对后续修正的影响时,这个方法不错。Momentum 的参数 momentum 控制了之前梯度的影响程度,一般取值在 0.8 到 0.9 之间。
-
Adagrad:Adagrad 会为不经常更新的参数提供更大的学习率,适合处理稀疏数据。
-
RMSprop:与 Adam 类似,RMSprop 也是自适应学习率的一种算法。在一些情况下,它可能会比 Adam 更好。
-
Adam:Adam 通过自适应调整学习率来提高训练效率。它通常对于大多数问题都是一个良好的默认选择。
-
Adadelta:Adadelta 是一种自适应学习率的优化器,可以自动调整学习率。
-
Nadam:Nadam 是结合了 Nesterov 动量的 Adam 变体,通常在训练深度神经网络时表现良好。
-
FTRL:FTRL 是针对线性模型优化的一种算法,对于大规模线性模型可以很有效。
联系我 交流请署名👇

相关文章:

简单介绍神经网络中不同优化器的数学原理及使用特性【含规律总结】
当涉及到优化器时,我们通常是在解决一个参数优化问题,也就是寻找能够使损失函数最小化的一组参数。当我们在无脑用adam时,有没有斟酌过用这个是否合适,或者说凭经验能够有目的性换用不同的优化器?是否用其他的优化器可…...

JL653—一个基于ARINC653的应用程序仿真调试工具
JL653是安装在PC机Windows操作系统上面的一层接插件,它能够真实地模拟ARINC653标准规定的功能性行为,从而可以供研发人员在PC机Windows环境下高效、快速的进行基于ARINC653的应用程序的开发、调试等。 JL653提供了ARINC 653 Part 1中要求的以下服务&…...
MQTT Paho Android 支持SSL/TLS(亲测有效)
MQTT Paho Android 支持SSL/TLS(亲测有效) 登录时支持ssl的交互 这是调测登录界面设计 代码中对ssl/tls的支持 使用MqttAndroidClient配置mqtt客户端请求时,不加密及加密方式连接存在以下几点差异: url及端口差异 val uri: String if (tlsConnect…...
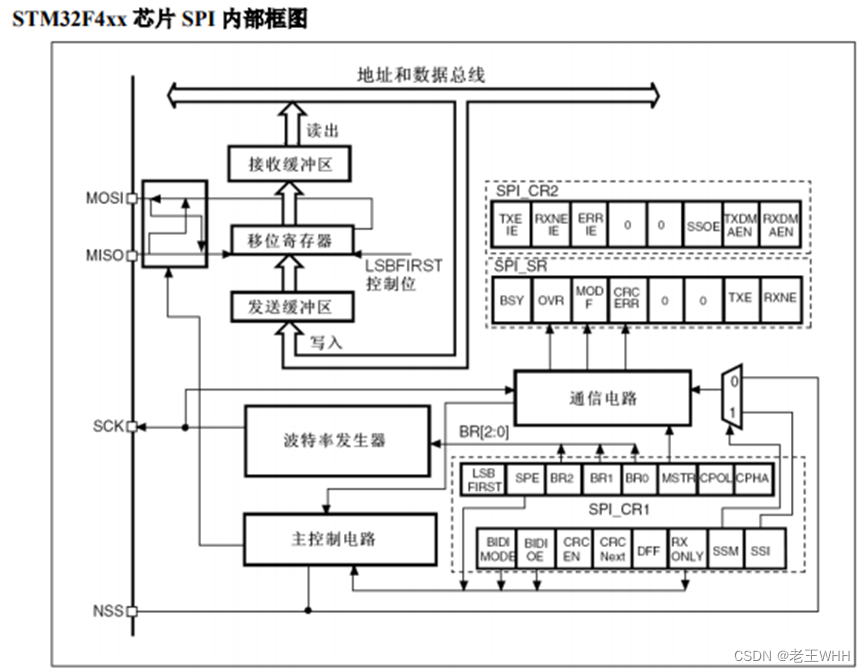
STM32——SPI通信
文章目录 SPI(Serial Peripheral Interface)概述:SPI的硬件连接:SPI的特点和优势:SPI的常见应用:SPI的工作方式和时序图分析:工作模式传输模式与时序分析工作流程 SPI设备的寄存器结构和寄存器设…...

Linux虚拟机局域网IP配置
前言 应用程序包部署在主机(Window)的虚拟机(Linux CentOS7)上,把主机当做一个服务器,在局域网中访问部署在主机上的应用程序,配置Linux网络。 文章如有侵权,无意为之,…...

MacOS删除.DS_Store文件
目录 .DS_Store是什么删除命令防止再生命令 .DS_Store是什么 在 Mac OS X 系统下,几乎绝大部分文件夹中都包含 .DS_Store 隐藏文件,这里保存着针对这个目录的特殊信息和设置配置,例如查看方式、图标大小以及这个目录的一些附属元数据。 而在…...
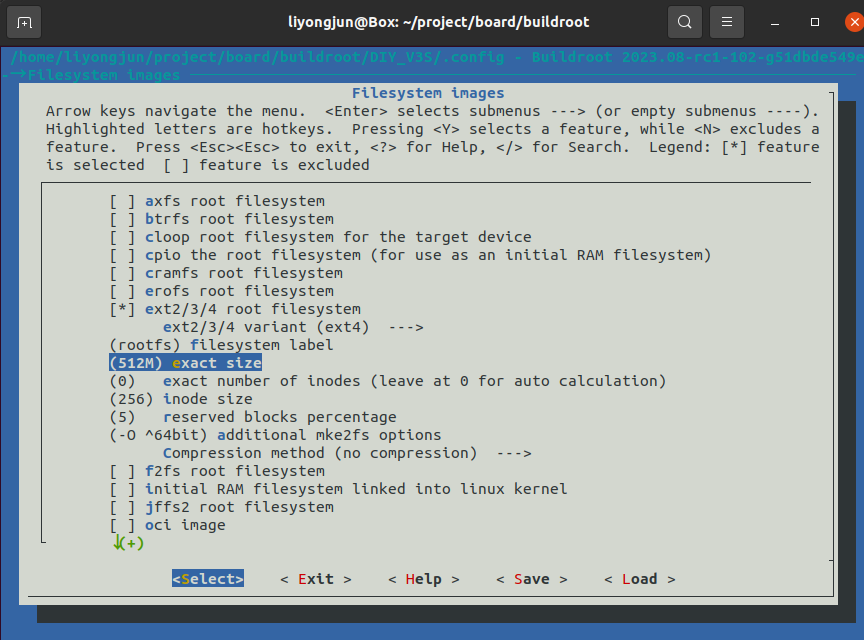
ARM Linux DIY(十一)板子名称、开机 logo、LCD 控制台、console 免登录、命令提示符、文件系统大小
文章目录 前言板子名称uboot Modelkernel 欢迎词、主机名 开机 logoLCD 控制台console 免登录命令提示符文件系统大小 前言 经过前面十篇文章的介绍,硬件部分调试基本完毕,接下来的文章开始介绍软件的个性化开发。 板子名称 uboot Model 既然是自己的…...

【Unity程序技巧】Unity中的单例模式的运用
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:Uni…...
最长连续数列,移动零)
java leetcodetop100 (3,4 )最长连续数列,移动零
top3 最长连续数列 给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。 * * 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 * * * * 示例 1: * * 输入:nums [100,…...
用Vite从零到一创建React+ts项目
方式一:使用create-react-app命令创建项目 1、使用以下命令初始化一个空的npm 项目 npm init -y 2、输入以下命令安装React npm i create-react-app ps:如果失败的话尝试(1:使用管理员身份执行命令(2:切换镜像重…...
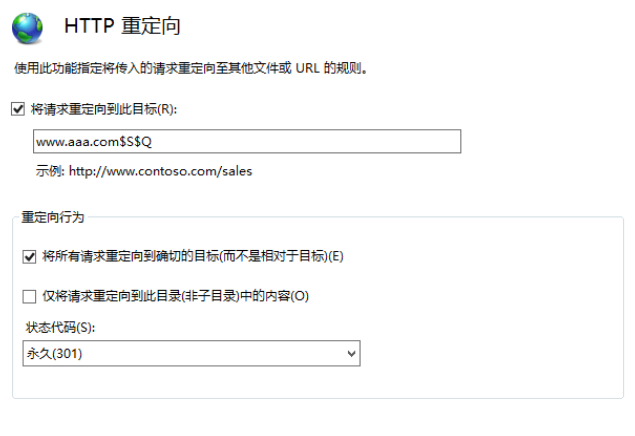
HTTP状态码301(永久重定向)不同Web服务器的配置方法
文章目录 301状态码通常在那些情况下使用301永久重定向配置Nginx配置301永久重定向Windows配置IIS301永久重定向PHP下的301重定向Apache服务器实现301重定向 301重定向是否违反相关法规?推荐阅读 当用户或搜索引擎向服务器发出浏览请求时,服务器返回的HT…...
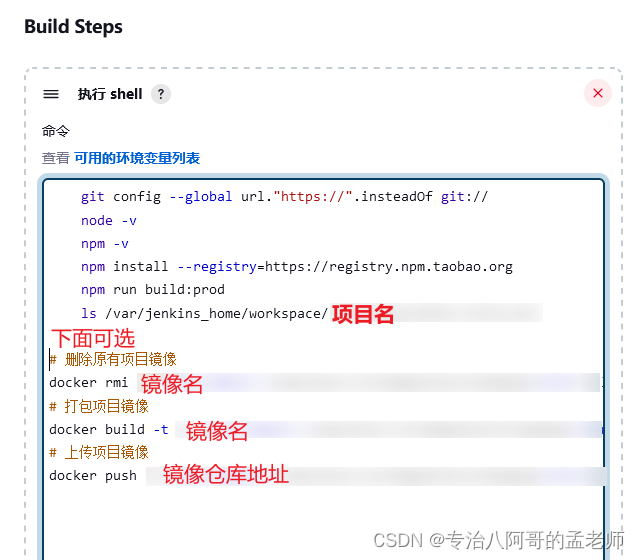
vue-element-admin项目部署 nginx动态代理 含Docker部署、 Jenkins构建
介绍三种方式: 1.直接部署到nginx中 2.用nginx docker镜像部署 3.使用Jenkins构建 1.直接用nginx部署 vue-element-admin项目下有两个.env文件,.env.production是生产环境的,.env.developpment是开发环境的 vue-element-admin默认用的是mock数…...
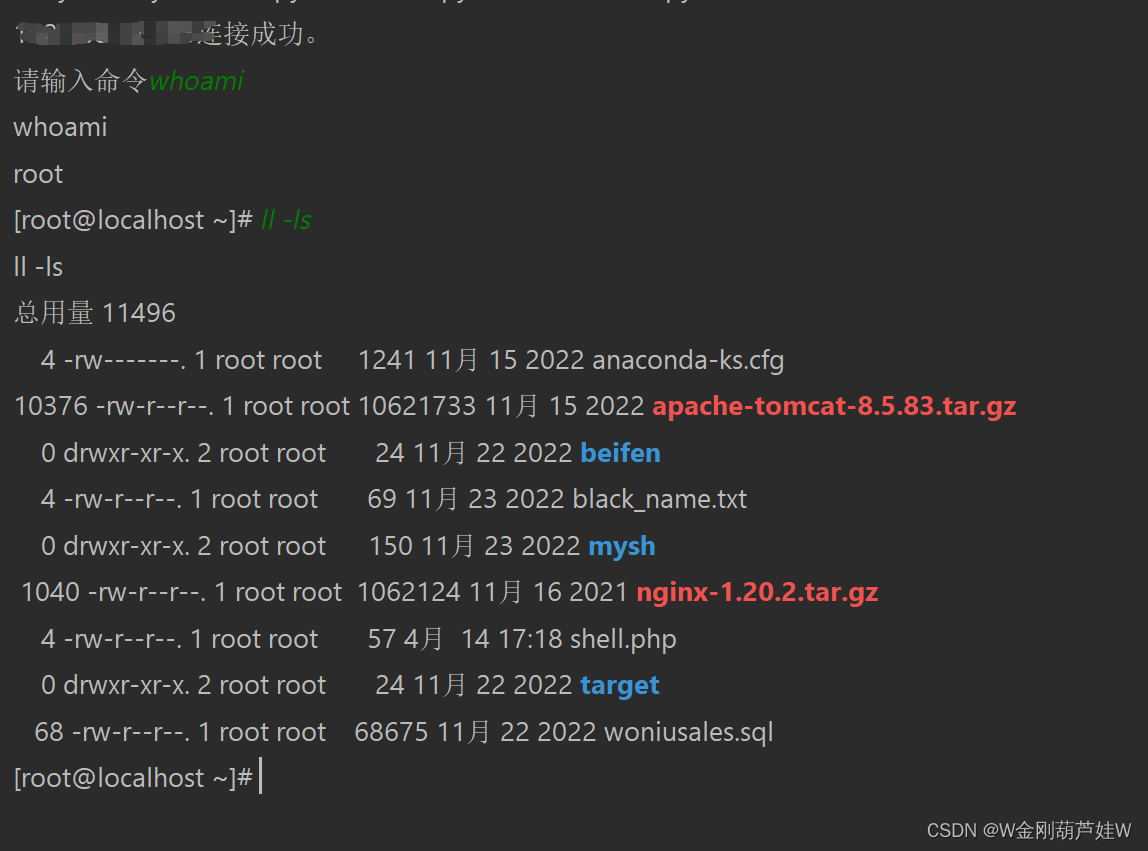
使用Python来写模拟Xshell实现远程命令执行与交互
一、模块 这里使用的是 paramiko带三方库 pip install paramiko二、效果图 三、代码实现(这里的IP,用户名,密码修改为自己对应服务器的) import paramiko import timeclass Linux(object):# 参数初始化def __init__(self, ip, us…...

mybatis 数据库字段为空or为空串 忽略条件过滤, 不为空且不为空串时才需nameParam过滤条件
name未配置视为不考虑name条件 select * from user where (( (ISNULL(name)) OR (name) ) OR name #{user.nameParam} ) 三个or语句 推荐这个 select * from user where ISNULL(name) OR name OR name #{user.nameParam} select * from user where ISNULL(name) OR …...
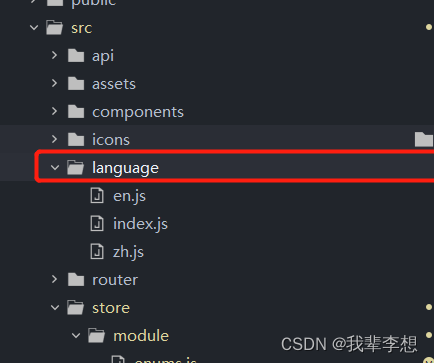
【玩玩Vue】通过vue-store实现枚举管理,用于下拉选项和中英文翻译等
原文作者:我辈李想 版权声明:文章原创,转载时请务必加上原文超链接、作者信息和本声明。 文章目录 一、store基础用法1.在src下新建store文件夹,在store下新建module文件夹2.在module下新建enums.js文件3.在store下新建getters.js…...

ISCSI:后端卷以LVM 的方式配置 ISCSI 目标启动器
写在前面 准备考试整理相关笔记博文内容涉及使用 LVM 做ISCSI 目标后端块存储 Demo理解不足小伙伴帮忙指正 对每个人而言,真正的职责只有一个:找到自我。然后在心中坚守其一生,全心全意,永不停息。所有其它的路都是不完整的&#…...

八公山豆腐发展现状与销售对策研究
1.引言 八公山豆腐作为中国传统特色食品之一,一直以来备受人们的喜爱。然而,在现代社会中,由于消费者对于营养健康的追求以及市场竞争的加剧,八公山豆腐的市场份额逐渐缩小。因此,为了更好地推广和发展八公山豆腐&…...

排序算法-插入排序
属性 当插入第i(i>1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移 直接插入排序…...
数码管显示)
多位数按键操作(闪烁)数码管显示
/*----------------------------------------------- 内容:按键加减数字,多个数码管显示 ------------------------------------------------*/ #include<reg52.h> //包含头文件,一般情况不需要改动,头文件包含特殊功能寄存…...

MyEclipse项目导入与导出
一、项目导出 1、右键选择项目名称,弹出菜单中选择“export”,如下图所示 2、选择“恶心“export”,弹出菜单如下;在“General“选项中,选择“File System”选项 3、点击“next”,进入保存位置选择界面&am…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...
