(超详解)堆排序+(图解)
目录:
1:如何建堆(两种方法)
2:两种方法建堆的时间复杂度分析与计算
3:不同类型的排序方式我们应该如何建堆
文章正式开始:
1:如何建堆
在实现堆排序之前我们必须得建堆,才能够实现堆排序
首先在讲解如何建堆之前让我们先来回顾一下堆的概念,堆是一种完全二叉树,它有两种形式,一种是大根堆,另外一种是小根堆。
大根堆:所有的父亲结点大于或等于孩子结点。
小根堆:所有的父亲结点小于或等于孩子结点。
本文在介绍堆排序的时候我们都默认排升序。
方法1:我们采用向上调整算法建堆
我们知道向上调整算法的前提是前面的数必须是堆,所以我们就形成了一种思路:
第一个数我们可以看成是一个堆,那么从第二个数开始我们就依次采用向上调整算法,这样最后我们的数字就会形成一个堆。
图解:

向上调整建堆的代码如下,如果不理解可以自己尝试画图:
//假设排升序,建大堆
void HeapSort(int* a, int n){//先建堆,用向上调整算法for (int i = 1; i < n; i++){AdjustUp(a, i);}}方法2:采用向下调整的思路建堆
向下调整的前提:要调整的对象左右子树都得是堆
那么我们如何通过一个数组来原地建堆呢?
其实我们可以这样想,叶子结点既可以看作是大堆,也可以看作是小堆,所以我们可以从后面往前面来建堆。
思路:找到倒数第一个非叶子结点,这样我们可以保证左右子树都是堆,才能够对整个堆使用向下调整算法的思想。
那么最后一个非叶子结点如何才能找到呢?这里不就是我们要记住的一个特点吗,通过孩子结点来算父亲结点。
parent=(child-1)/2;
我们先找到最后一个结点的下标,然后通过结点算父亲的公式不就可以算出来了吗
所以倒数第一个非叶子结点的下标不就是 (n-1-1)/2吗 ?
图解过程:
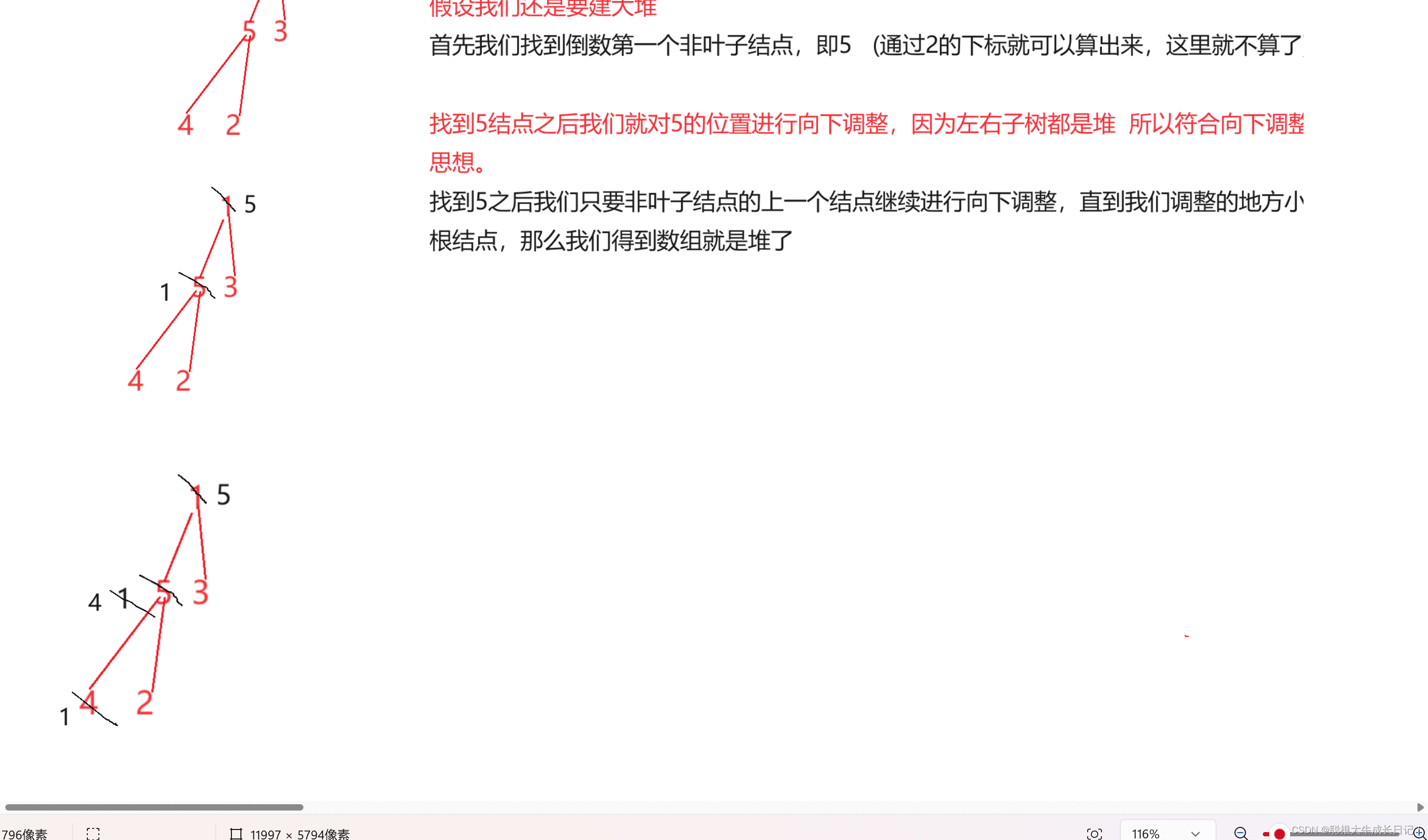
2:两种方法建堆复杂度的分析
首先我们直接公布结论:
向上调整算法的时间复杂度为O(N*logN),向下调整算法的时间复杂度为O(N),所以建堆在复杂度的层面来说向下调整算法是优于向上调整算法的。
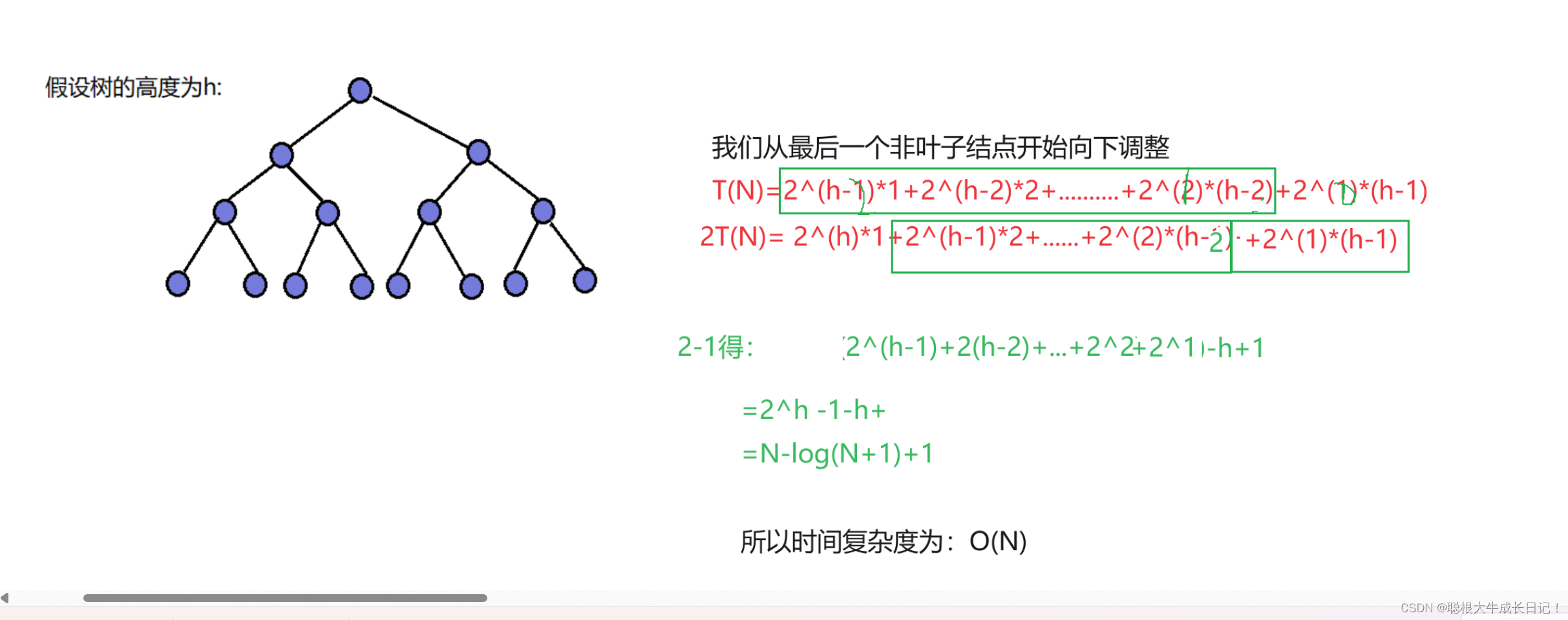
向上调整算法的时间复杂度分析:
我们知道向上调整算法是依次将后一个元素向上进行调整,那么最坏的情况下就是我们所插入一个数就要调整到根节点处。
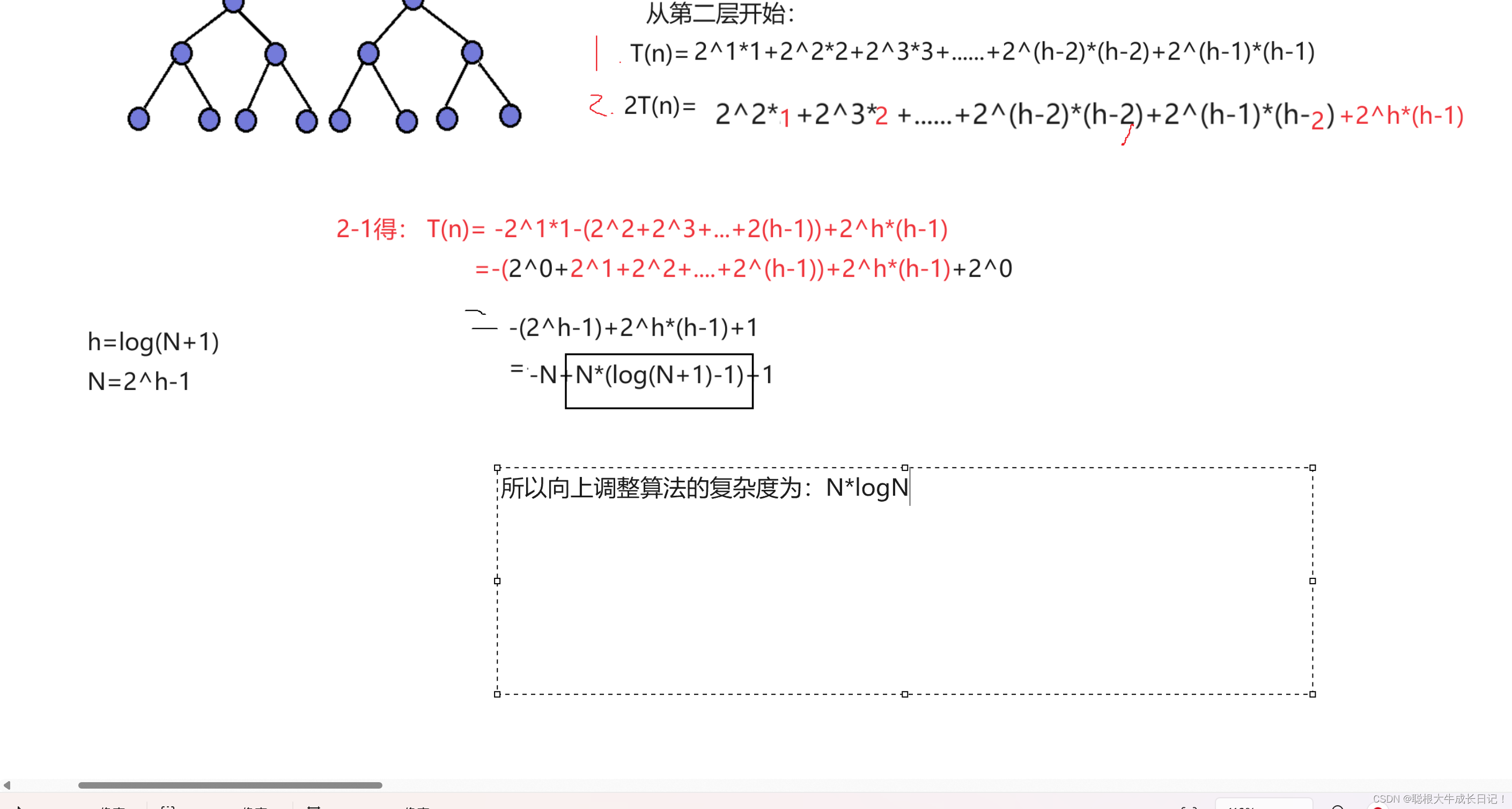
同理向下调整的复杂度分析
为啥同样都是建堆的过程,可是为啥向下调整算法的时间复杂度优于向上调整算法呢
因为向下调整算法时,最后一层结点不需要向下调整,且最后一层的结点比较多,从下往上,结点个数变少,乘以的层数变多,但是主要取决于时间复杂度的是结点个数多的。
而向上调整算法,最后一层结点的个数多,且需要调整的层数也最高,导致向上调整的时间复杂度高。
3.堆排序
在讲了前面两种算法的基础上我们就可以来谈一谈我们的堆排序了,堆排序并不是我们所讲的数据结构,虽然说堆数据结构也可以看出堆的升序与降序,但是我们可能并不是只要打印这个数组出来,我们可能还会进行一些算法,比如2分查找....。
堆排序的思路:
1:首先对数组进行建堆。
2:将最后一个元素与第一个元素交换,在向下进行调整
3:循环往复的进行,最后排除来的就是我们所需要的结果了。
那我们在排升序的时候应该见建大堆,还是小堆呢?
相信许多人在看到要排升序的时候,可能第一反应的是建小堆,因为小堆中的第一个数是所有元素中最小的那个数,但是当我们建立小堆的时候,那我们的第二个小的数字如何取呢?
且当我们将第一个元素排好之后,后面的元素的关系都不对了,就会形成兄弟变父子,父子叔侄变兄弟,那么我们可能还需要建一次堆,那么总体的时间复杂度为N*(N*logN),
所以我们排升序需要建大堆,排降序需要建小堆。
而我们为什么可以这样子做呢?
我们假设有一个数组我们已近将他建成大堆了,那么我们很明显知道根节点最大,那么我们就可以这样子做。
将最大的根结点与最后一个数字进行交换,由于我们只是交换了根结点与最后一个元素,其他的结构没有动,所以就可以使用向下调整,然后在对前n-1个元素进行向下调整,整个的时间复杂度为logn。每次选一个大的,我们向将大的排在最后,循环进行就可以排成我们所需要的结果了。
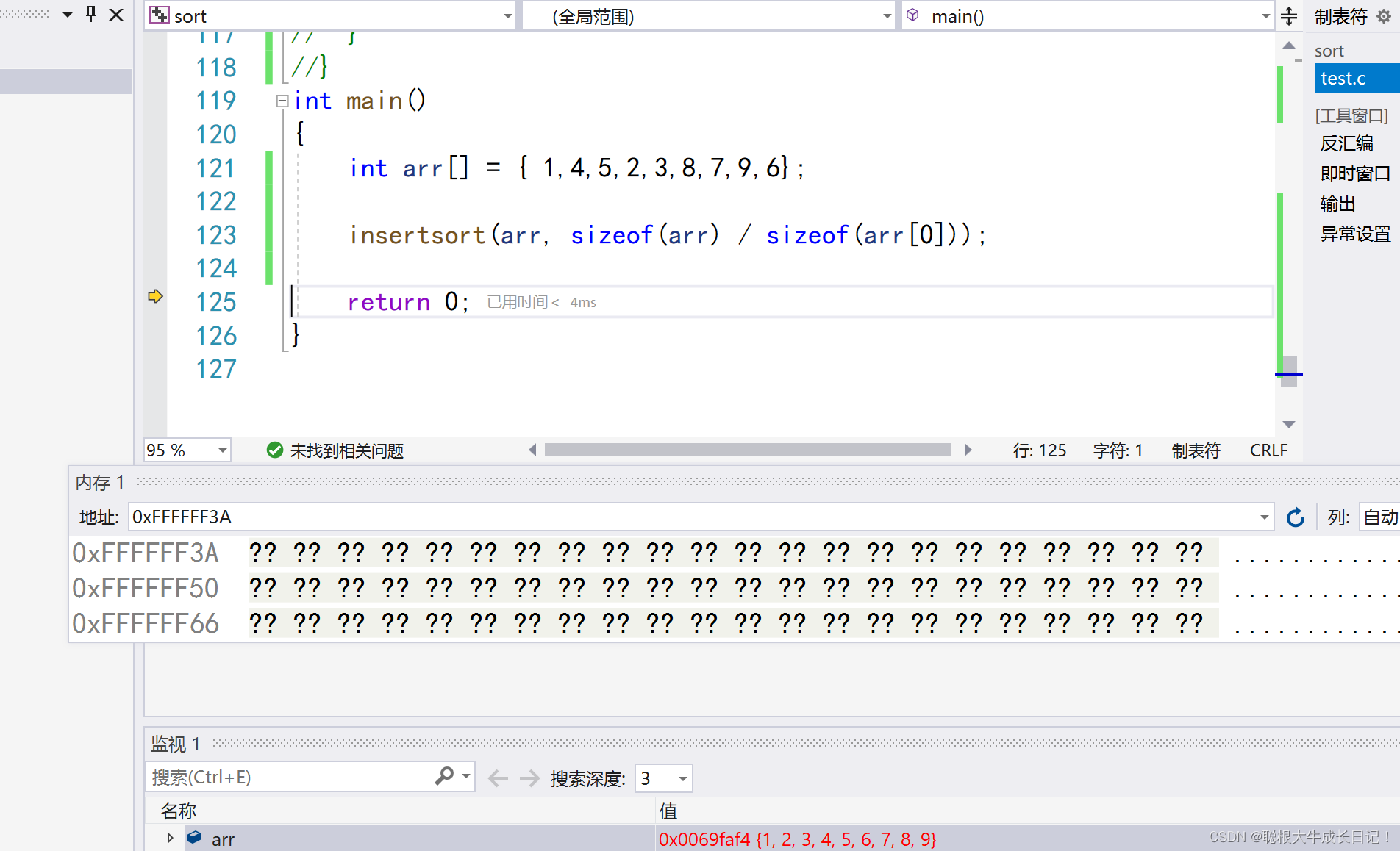
代码实现
void HeapSort(int* a, int n)
{//向下调整算法建堆,建大堆,排升序for (int i = (n-1-1)/2; i >=0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}也可以使用向上调整建堆进行堆排序:
假设排升序,建大堆
//void HeapSort(int* a, int n)
//{
// //先建堆,用向上调整算法
// for (int i = 1; i < n; i++)
// {
// AdjustUp(a, i);
// }
//
// //将最后一个数与根节点交换
// //在进行向下调整,循环执行
// int end = n - 1;
// /*while (end > 0)
// {
// Swap(&a[end], &a[0]);
// AdjustDown(a, end, 0);
// --end;
// }*/
//
//
//
//
//}
本章完!!!
感谢观看。
相关文章:

(超详解)堆排序+(图解)
目录: 1:如何建堆(两种方法) 2:两种方法建堆的时间复杂度分析与计算 3:不同类型的排序方式我们应该如何建堆 文章正式开始: 1:如何建堆 在实现堆排序之前我们必须得建堆,才能够实现堆排序 首先在讲解如何建堆之前让我们先来回顾一…...

Hadoop的YARN高可用
一、YARN简介 Hadoop2.0即第二代Hadoop,由分布式存储系统HDFS、并行计算框架MapReduce和分布式资源管理系统YARN三个系统组成,其中YARN是一个资源管理系统,负责集群资源管理和调度,MapReduce则是运行在YARN上的离线处理框架。 Y…...

C++内存检查
内存泄漏是程序中常见,也是最令人痛苦的一种bug。好在有一些检查工具可以帮助我们,这里介绍一个google 提供的简单直接的工具 Address-Sanitizer (ASAN)。 预备条件 ASAN 原来是LLVM 中的特性,后来GCC 4.8中也开始支持。也就是说࿰…...

防火墙概述及实战
目录 前言 一、概述 (一)、防火墙分类 (二)、防火墙性能 (三)、iptables (四)、iptables中表的概念 二、iptables规则匹配条件分类 (一)、基本匹配条…...
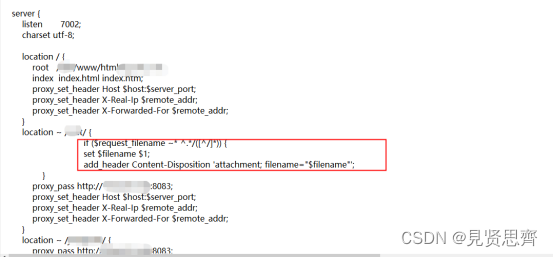
nginx代理故障总结
一、故障现象 今天公司的某个系统文件下载功能失败,报错network error,其他功能正常。 二、故障定位 首先我们检查了公司的网络情况,包括网络路由、防火墙策略、终端安全产品等,均未发现异常。 尝试访问http://X.X.X.X:7002端口&…...
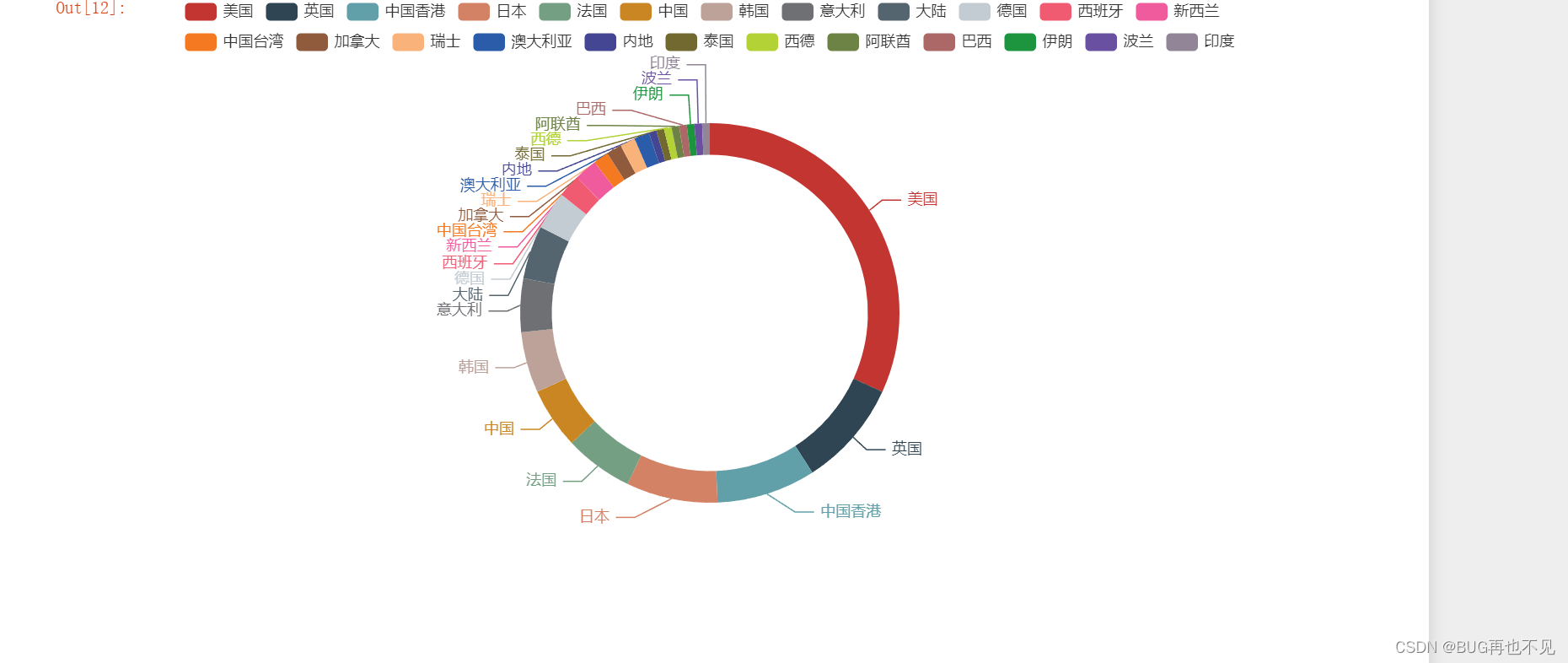
python爬虫爬取电影数据并做可视化
思路: 1、发送请求,解析html里面的数据 2、保存到csv文件 3、数据处理 4、数据可视化 需要用到的库: import requests,csv #请求库和保存库 import pandas as pd #读取csv文件以及操作数据 from lxml import etree #解析html库 from …...
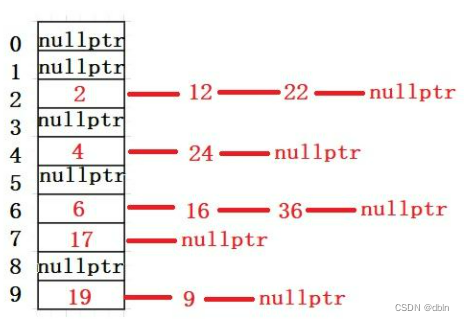
哈希及哈希表的实现
目录 一、哈希的引入 二、概念 三、哈希冲突 四、哈希函数 常见的哈希函数 1、直接定址法 2、除留余数法 五、哈希冲突的解决 1、闭散列 2、开散列 一、哈希的引入 顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系,因此在查找…...
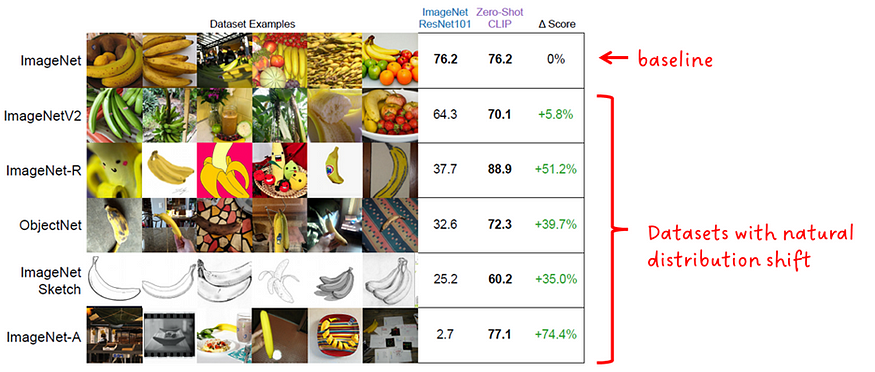
CLIP 基础模型:从自然语言监督中学习可转移的视觉模型
一、说明 在本文中,我们将介绍CLIP背后的论文(Contrastive Language-I mage Pre-Training)。我们将提取关键概念并分解它们以使其易于理解。此外,还对图像和数据图表进行了注释以澄清疑问。 图片来源: 论文:…...

解读性能指标TP50、TP90、TP99、TP999
TP指标说明 TP指标: 指在一个时间段内,统计该方法每次调用所消耗的时间,并将这些时间按从小到大的顺序进行排序, 并取出结果为:总次数*指标数对应TP指标的值,再取出排序好的时间。 TPTop Percentile,Top百分数&#…...

【无标题】mysql 截取两个,之间字符串
截取两个,之间字符串 select area,SUBSTRING_INDEX(et.area,,,1) as XZQH1,if(length(et.area)-length(replace(et.area,,,))>1,SUBSTRING_INDEX(SUBSTRING_INDEX(et.area,,,2),,,-1),NULL) AS XZQH2,if(length(et.area)-length(replace(et.area,,,))>2,SUBS…...

全局的键盘监听事件
一、设定全局键盘监听事件 放在vue 的created()或者mounted ()中,可对整个文档进行键盘事件监听。 new Vue({ created() { window.addEventListener(keydown, this.handleKeydown); }, beforeDestroy() { window.removeEventListener(keydown, this.handleK…...
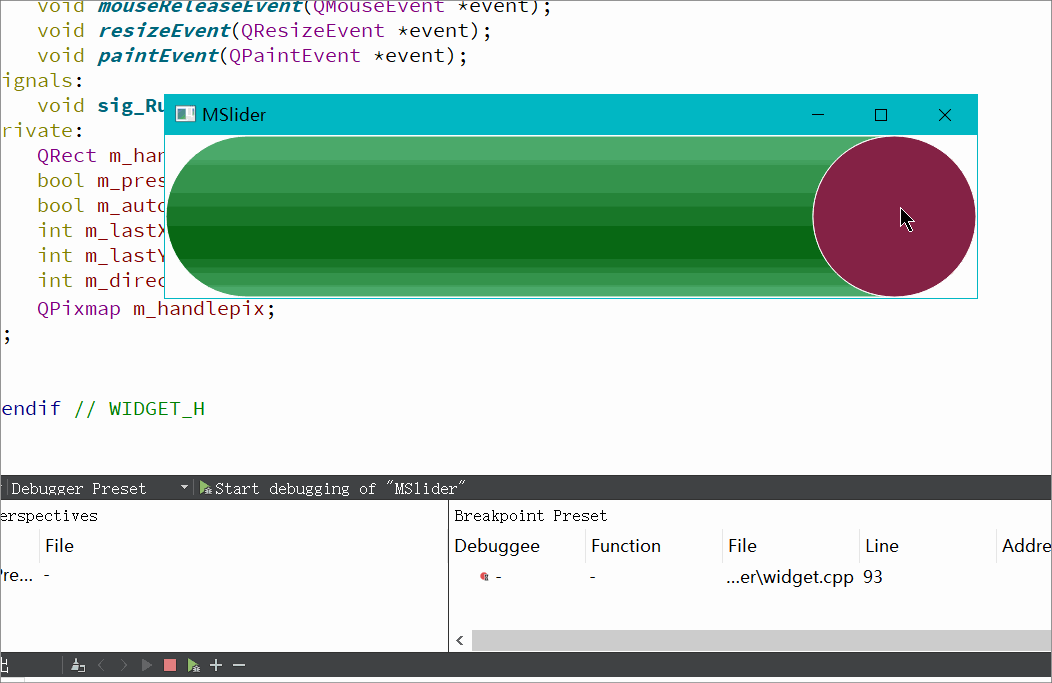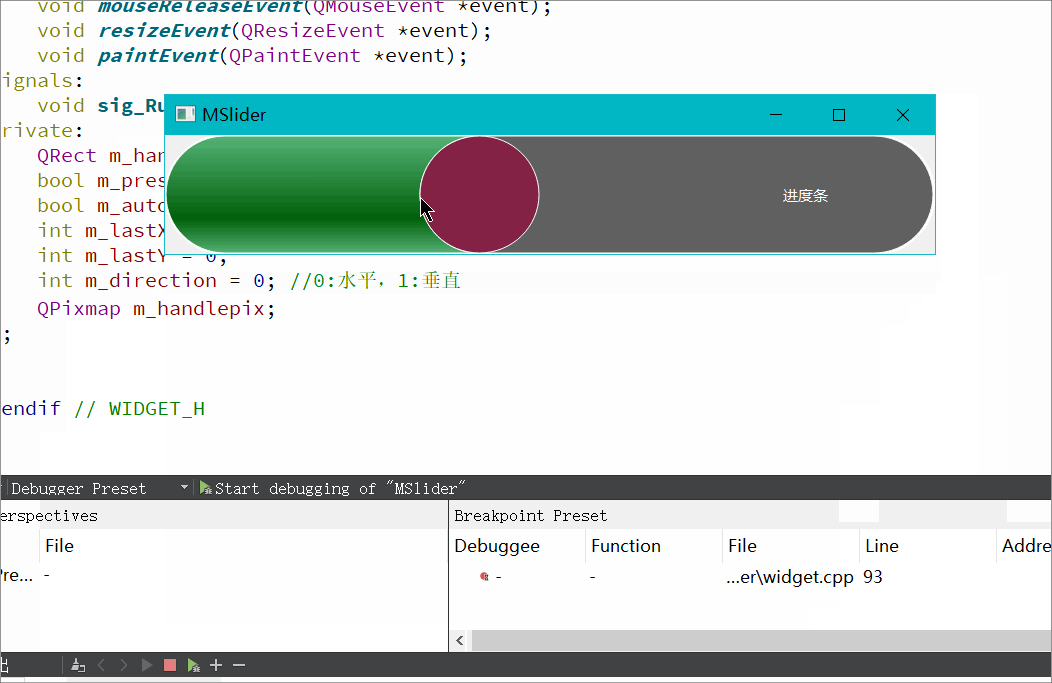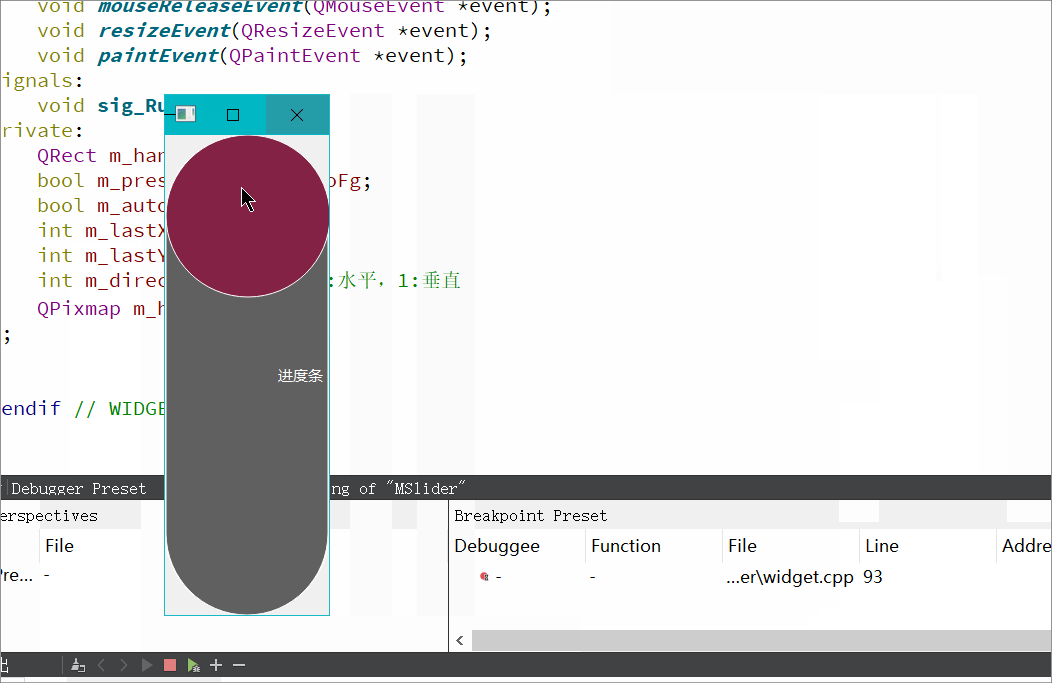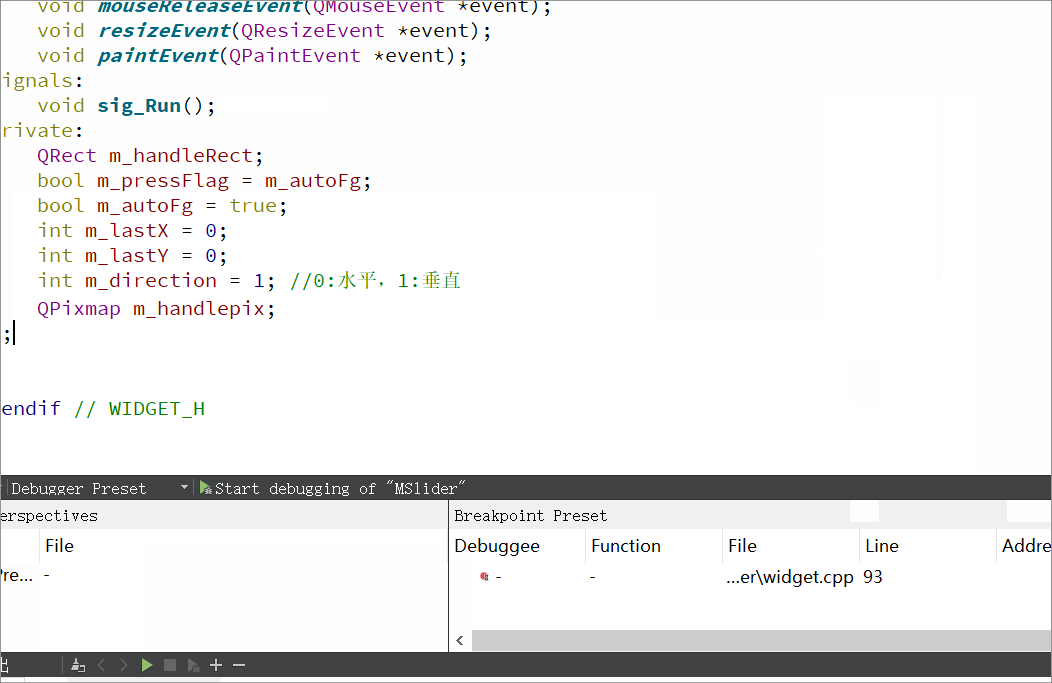
Qt自定义QSlider(支持水平垂直)
实现背景: Qt本身有自己的QSlider,为什么我们还要自定义实现呢,因为Qt自带的QSlider存在一个问题,当首尾为圆角时,滑动滚动条到首尾时会出现圆角变成矩形的问题。当然如果QSS之间的margin和滑动条的圆角控制的好的话是…...

会话控制学习
文章目录 介绍cookieexpress中使用cookie获取cookie session配置区别 介绍 cookie express中使用cookie 退出登录就是删除cookie 获取cookie 添加中间键后,直接获取 session 配置 区别...

dweb-browser阅读
dweb-browser阅读 核心模块js.browser.dwebjmm.browser.dwebmwebview.browser.dwebnativeui.browser.dweb.sys.dweb plaoc插件 核心模块 js.browser.dweb 它是一个 javascript-runtime,使用的是 WebWorker 作为底层实现。它可以让您在 dweb-browser 中运行 javasc…...

ChatGPT:使用fastjson读取JSON数据问题——如何使用com.alibaba.fastjson库读取JSON数据的特定字段
ChatGPT:使用fastjson读取JSON数据问题——如何使用com.alibaba.fastjson库读取JSON数据的特定字段 有一段Json字符串: {"code": 200,"message": "success","data": {"total": "1","l…...
2、ARM处理器概论
一、ARM处理器概述 1、ARM的含义 ARM(Advanced RISC Machines)有三种含义,一个公司的名称、一类处理器的通称、一种技术 ARM公司: 成立于1990年11月,前身为Acorn计算机公司主要设计ARM系列RISC处理器内核授权ARM内…...
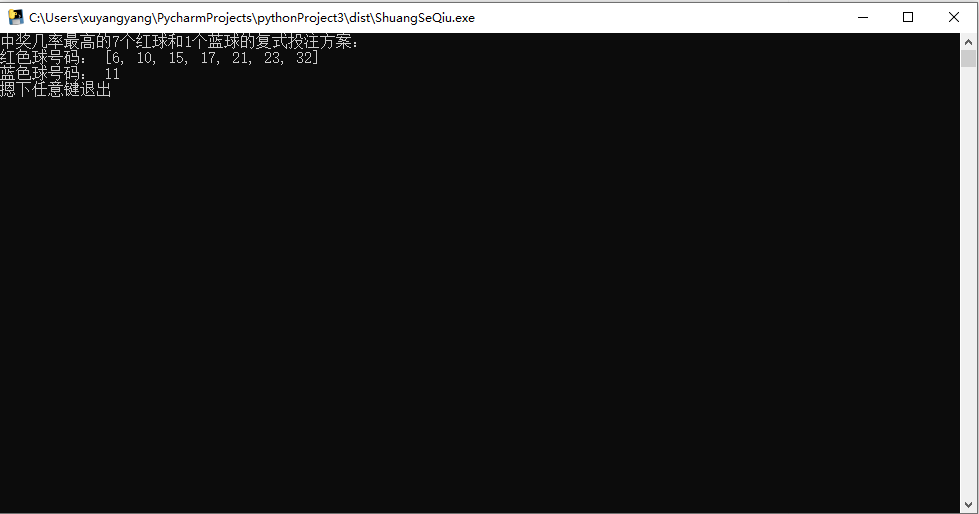
【Python】福利彩票复式模拟选号程序
【效果】 【注意】 逻辑是用Random模拟10000次复试彩票选号,然后给出最大可能性一组。但是模拟终究是模拟,和现实彩票结果没有任何联系,下载下来玩就是了,没人能保证模拟出中奖号码,不要投机,不要投机! 【修改】 代码很简单,如果想改成不是复式的,自行修改即可。 如…...

Pytorch 机器学习专业基础知识+神经网络搭建相关知识
文章目录 一、三种学习方式二、机器学习的一些专业术语三、模型相关知识四、常用的保留策略五、数据处理六、解决过拟合与欠拟合七、成功的衡量标准 一、三种学习方式 有监督学习: 1、分类问题 2、回归问题 3、图像分割 4、语音识别 5、语言翻译 无监督学习 1、聚类…...

torch 和paddle 的GPU版本可以放在同一个conda环境下吗
新建conda 虚拟环境,python 版本3.8.17 虚拟机,系统centos 7,内核版本Linux fastknow 3.10.0-1160.92.1.el7.x86_64 ,显卡T4,nvidia-smi ,460.32.03,对应cuda 11.2,安装cuda 11.2和cudnn,conda…...

MYBATIS-PLUS入门使用、踩坑记录
转载: mybatis-plus入门使用、踩坑记录 - 灰信网(软件开发博客聚合) 首先引入MYBATIS-PLUS依赖: SPRING BOOT项目: <dependency><groupId>com.baomidou</groupId><artifactId>mybatis-plus…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...