数据结构—堆(完全解析)
数据结构—堆(完全解析)
数据结构——堆(Heap)大根堆、小根堆
详解数据结构——堆
堆的基本存储
【从堆的定义到优先队列、堆排序】 10分钟看懂必考的数据结构——堆
【堆/排序】堆排序的两种建堆方法
【算法】排序算法之堆排序
C++:浅析STL之priority_queue构建大根堆与小根堆
基本概念
堆通常是一个可以被看做一棵完全二叉树的数组对象
堆满足下列性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值
- 堆总是一棵完全二叉树
Min-heap(大根堆): 父节点的值小于或等于子节点的值
Max-heap(小根堆): 父节点的值大于或等于子节点的值

堆的存储
一般都用数组来表示堆,i结点的父结点下标就为(i–1)/2
它的左右子结点下标分别为2 * i + 1和2 * i + 2
如第0个结点左右子结点下标分别为1和2

堆的插入和上浮
- 当一个新元素想要插入这个堆的时候,我们首先把他放到这个堆的末尾
- 然后依据堆的特性,对它的位置进行调整,由于要保持父结点的值要永远少于其子节点的值,而
2的直接父节点6大于了它,所以要把他们两的位置对换 - 对换完毕后,再检查这个堆的状态,发现其父节点
3仍然大于自己,所以继续往上和3对换 - 结束后和
0比较,0不大于自己,所以停留在原地不动,插入结束 - 简单来说,插入一个结点就是将该元素插入到堆的尾部,然后不断上浮调整位置,直至满足堆的条件

堆的删除和下沉
- 删除一般指的都是删除堆顶元素,在堆顶元素被拿掉后,将末尾元素置换上来,进行下沉操作
- 由于这是最小堆,堆顶一定是最小元素,首先
6大于左结点1,需要下沉, - 下沉完以后继续和它子节点比较,发现左结点
2小于自身,继续下沉 - 最后
8和9都比6大,停止下沉。 - 总结来说,意思就是删除堆顶元素后,用末尾元素补上,然后不断下沉,直至满足堆的条件

堆的建立
自顶向下,时间复杂度为O(nlogn)

自下而上,时间复杂度为O(n)
从倒数第二排开始,对每一个父节点进行下滤操作,直到根节点操作完毕


堆的应用
优先队列
优先队列有两个操作,插入队列和弹出最小元素

优先队列利用小根堆实现,弹出根节点即可实现弹出最小元素的操作

弹出后要将剩余的元素调整为堆,将最后一个元素放到根节点,进行下沉操作即可


堆排序
- 先把数组构造成一个大顶堆(父亲节点大于其子节点),然后把堆顶(数组最大值,数组第一个元素)和数组最后一个元素交换,这样就把最大值放到了数组最后边
- 把数组度-1,再进行构造堆把剩余的第二大值放到堆顶,输出堆顶(放到剩余未排序数组最后面),依次类推,直至数组排序完成
#include <iostream>
#include <algorithm>
using namespace std;
void max_heapify(int arr[], int start, int end) {//建立父节点指标和子节点指标int dad = start;int son = dad * 2 + 1;while (son <= end) { //若子节点指标在范围内才做比较if (son + 1 <= end && arr[son] < arr[son + 1]) //先比较两个子节点大小,选择最大的son++;if (arr[dad] > arr[son]) //如果父节点大于子节点代表调整完毕,直接跳出函数return;else { //否则交换父子内容再继续子节点和孙节点比较swap(arr[dad], arr[son]);dad = son;son = dad * 2 + 1;}}
}
void heap_sort(int arr[], int len) {//初始化,i从最后一个父节点开始调整for (int i = len / 2 - 1; i >= 0; i--)max_heapify(arr, i, len - 1);//先将第一个元素和已经排好的元素前一位做交换,再从新调整(刚调整的元素之前的元素),直到排序完毕for (int i = len - 1; i > 0; i--) {swap(arr[0], arr[i]);max_heapify(arr, 0, i - 1);}
}
int main() {int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };int len = (int) sizeof(arr) / sizeof(*arr);heap_sort(arr, len);for (int i = 0; i < len; i++)cout << arr[i] << ' ';cout << endl;return 0;
}
C++ STL大根堆小根堆
在C++中优先队列默认的是大根堆,如果用小根堆则加入greater
#include <queue>
priority_queue<int, vector<int>>s;//大根堆
priority_queue<int, vector<int>, less<int>>s;//less表示按照递减(从大到小)的顺序插入元素,大根堆
priority_queue<int, vector<int>, greater<int>>s;//greater表示按照递增(从小到大)的顺序插入元素,小根堆
支持的顺序容器:vector,queue,默认是vector
priority_queue类能按照有序的方式在底层数据结构中执行插入、删除操作
q.pop();//删除优先队列priority_queuel的最高优先级元素(通过调用底层容器的pop_back()实现)
q.push(item);//在priority._queue优先级顺序合适的位置添加创建一个值为item的元素(通过调用底层容器的push_back()操作实现)
q.emplace(args);//在priority_queue优先级顺序合适的位置添加个由args构造的元素(通过调用底层容器的emplace_back()操作实现)
q.top();//返回priority_queue的首元素的引用(通过调用底层容器的front()操作实现)
q.empty();//判断q是否为空,空返回true,否则返回false(通过调用底层容器的empty()操作实现)
q.size();//返回q中的元素个数(通过调用底层容器的size()操作实现)
swap(q,p);//交换两个优先队列priority_queue p,q的内容,p和q的底层容器类型也必须相同(通过调用底层容器的swap0操纵实现)
相关文章:

数据结构—堆(完全解析)
数据结构—堆(完全解析) 数据结构——堆(Heap)大根堆、小根堆 详解数据结构——堆 堆的基本存储 【从堆的定义到优先队列、堆排序】 10分钟看懂必考的数据结构——堆 【堆/排序】堆排序的两种建堆方法 【算法】排序算法之堆排序 C…...

深度卷积对抗神经网络 进阶 第三部分 GANs Unpaired Translation with Cycle GAN 模型
非配对的图像转换应用 Unpaired Image-to-Image Translation Unpaired image-to-image translation 主要用于学习两组图像之间的对应关系,检查和寻找两堆数据中的共同内容(content)以及每堆独有的特点(style)。而这个…...

常见的排序算法 | 直接插入排序 | 希尔排序 | 选择排序 | 堆排序 | 冒泡排序 | 快速排序 | 归并排序 |(详解,附动图,代码)
思维导图: 一.插入排序 1.直接插入排序(InsertSort) ①手机通讯录时时刻刻都是有序的,新增一个电话号码时,就是使用插入排序的方法将其插入原有的有序序列。 ②打扑克 步骤: ①如果一个序列只有一个数&am…...
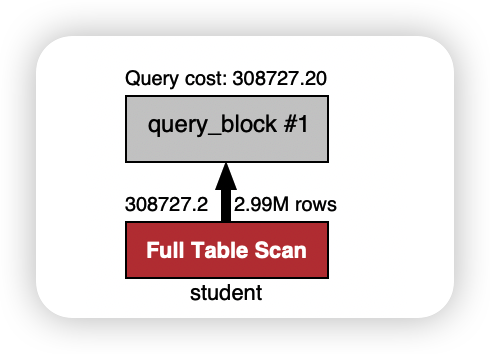
深入浅出 MySQL 索引(一)
MySQL 索引(基础篇) 你好,我是悟空。 本文目录如下: 一、前言 最近在梳理 MySQL 核心知识,刚好梳理到了 MySQL 索引相关的知识,我的文章风格很多都是原理 实战的方式带你去了解知识点,所以…...

FinClip 的 2022 与 2023
相比往年,今年复盘去年与展望新年的文章来的稍慢一点。不过也希望能够借这篇文章,和关注 FinClip 的用户朋友们一起聊聊,我们在去年和今年的想法与计划。 2022 在过去的一年中,我们的身边发生了很多事情,这些事情在不…...
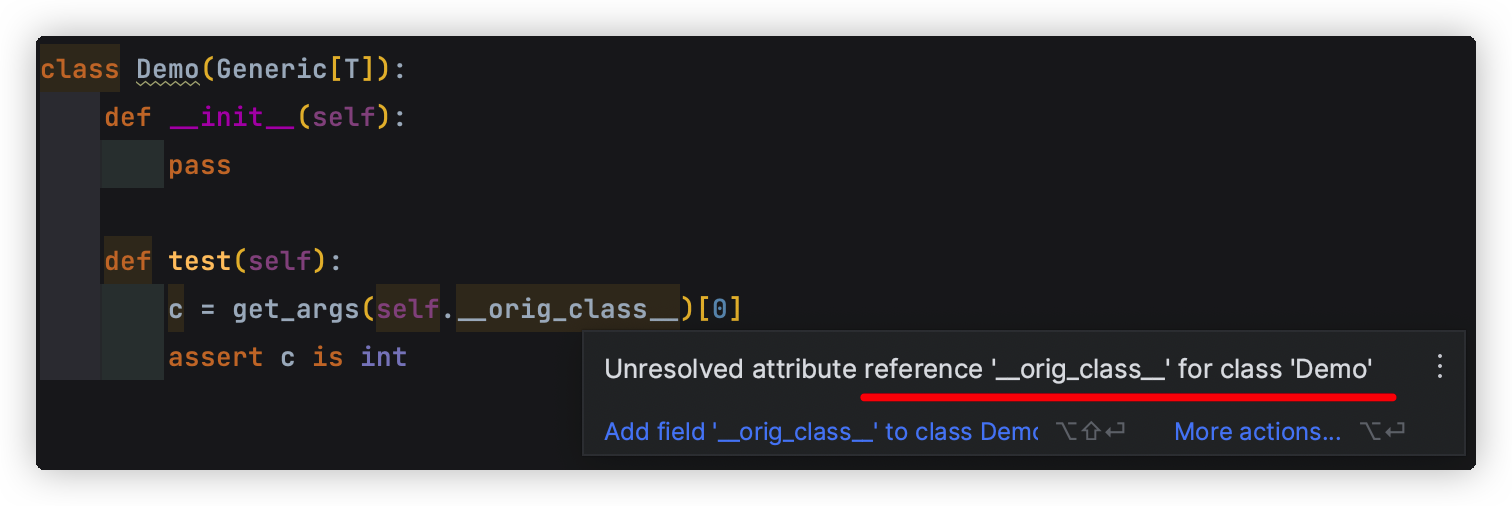
Python 泛型 - 如何在实例方法中获取泛型参数T的类型?
先上解决方法:https://stackoverflow.com/questions/57706180/generict-base-class-how-to-get-type-of-t-from-within-instance 再来简单分析下源码。 talk is cheap, show me the code. from typing import Dict Dict[str, int]Dict只是一个类型,并不…...

Shell语法基础总结
Shell 变量使用变量只读变量删除变量变量类型Shell 字符串单引号与双引号字符串获取字符串长度提取子字符串拼接字符串Shell 数组定义数组读取数组获取数组的长度Shell 传递参数Shell 基本运算符算术运算符关系运算符布尔运算符逻辑运算符字符串运算符Shell 信息输出命令Shell …...
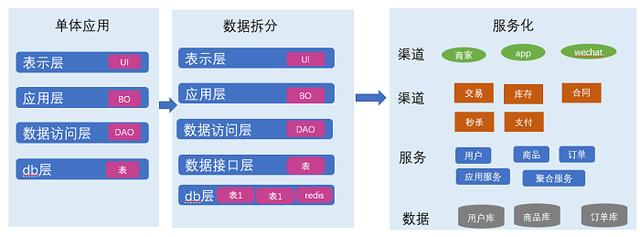
架构基本概念和架构本质
什么是架构和架构本质 在软件行业,对于什么是架构,都有很多的争论,每个人都有自己的理解。此君说的架构和彼君理解的架构未必是一回事。因此我们在讨论架构之前,我们先讨论架构的概念定义,概念是人认识这个世界的基础&…...

taobao.trade.ordersku.update( 更新交易的销售属性 )
¥开放平台免费API必须用户授权 只能更新发货前子订单的销售属性 只能更新价格相同的销售属性。对于拍下减库存的交易会同步更新销售属性的库存量。对于旺店的交易,要使用商品扩展信息中的SKU价格来比较。 必须使用sku_id或sku_props中的一个参数来更新&a…...
(附python代码实现))
算法实战应用案例精讲-【图像处理】使用scikit-image做图像处理(最终篇)(附python代码实现)
目录 高级滤波 autolevel bottomhat 与 tophat enhance_contrast entropy equalize gradient 其它滤波器...

数据结构与算法(四):树结构
前面讲到的顺序表、栈和队列都是一对一的线性结构,这节讲一对多的线性结构——树。「一对多」就是指一个元素只能有一个前驱,但可以有多个后继。 一、基本概念 树(tree)是n(n>0)个结点的有穷集。n0时称…...
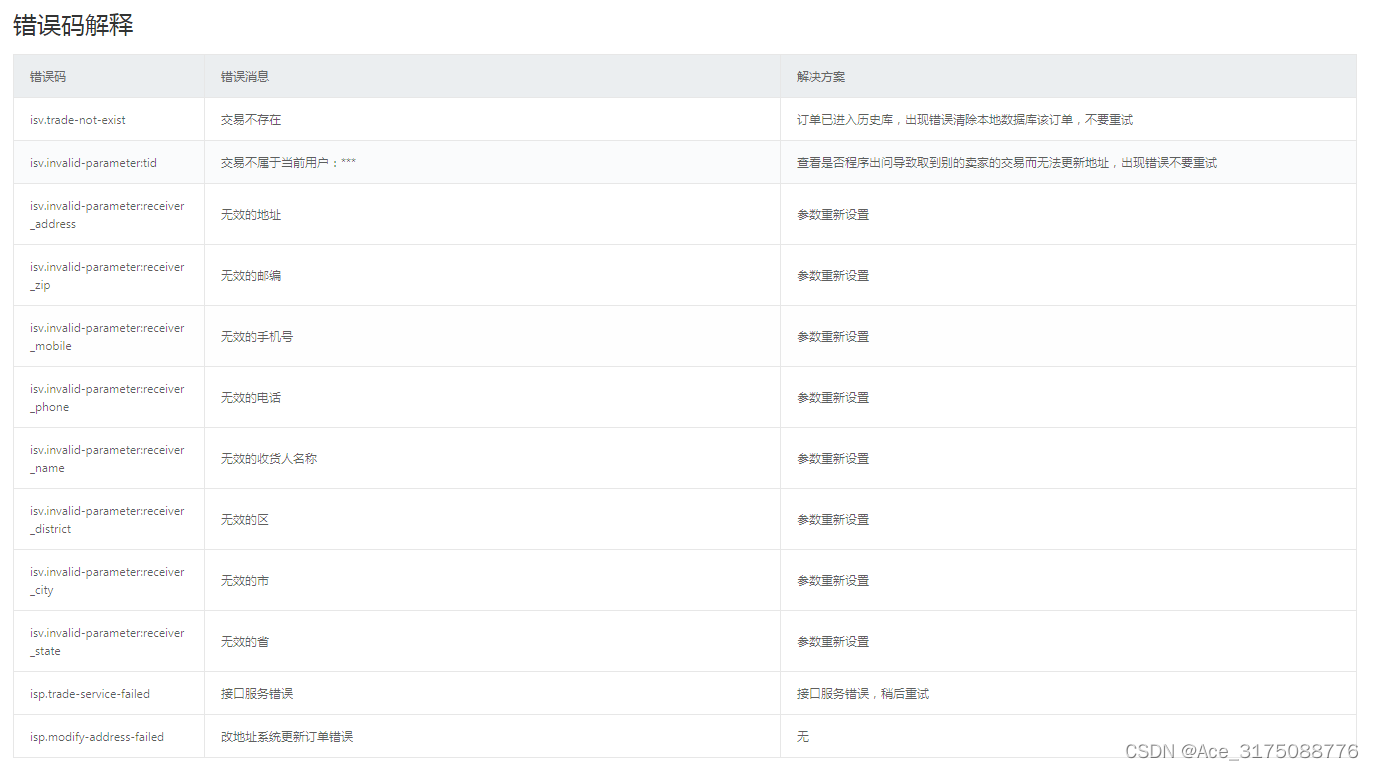
taobao.trade.shippingaddress.update( 更改交易的收货地址 )
¥开放平台免费API必须用户授权 只能更新一笔交易里面的买家收货地址 只能更新发货前(即买家已付款,等待卖家发货状态)的交易的买家收货地址 更新后的发货地址可以通过taobao.trade.fullinfo.get查到 参数中所说的字节为GBK编码的&…...
VS Code安装及(C/C++)环境配置(Windows系统)
参考资料2份: 从零开始的vscode安装及环境配置教程(C/C)(Windows系统)_光中影zone的博客-CSDN博客_vscode运行配置https://blog.csdn.net/qq_45807140/article/details/112862592 VSCode配置C/C环境 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/87864677 五…...
【Spring Cloud Alibaba】006-OpenFeign
【Spring Cloud Alibaba】006-OpenFeign 文章目录【Spring Cloud Alibaba】006-OpenFeign一、概述1、Java 项目实现接口调用的方法HttpclientOkhttpHttpURLConnectionRestTemplate WebClient2、Feign 概述二、Spring Cloud Alibaba 快速整合 OpenFeign1、添加依赖2、启动类加注…...

挚文集团短期内不适合投资,长期内看好
来源:猛兽财经 作者:猛兽财经 挚文集团(MOMO)在新闻稿中称自己是“中国在线社交和娱乐领域的领军企业”。 该公司旗下的陌陌是中国“陌生人社交网络”移动应用类别的领导者,并在2022年9月拥有超过1亿的月活跃用户。探…...

clion开发的常用快捷键以及gitcrlf的问题
前段报错:git config core.autocrlf false 然后删除app目录下的文件,除了.git文件夹然后 git bash ,执行 git reset --hardclion常用快捷键:Double shift 搜索文件F9调试F9运行到断点Ctrl F8 打断点F7单步步入Shift F8 单步跳出F8执行下一行代…...

LeetCode 格雷编码问题
格雷编码格雷编码的定义格雷编码的码表LeetCode 89. 格雷编码实例思路与代码思路一:找规律代码一代码二思路二:与自然数之间的关系(你必须知道,这个规律要去百度才知道)代码一LeetCode 1238. 循环码排列实例思路与代码…...

java生成html文件输出到指定位置
String fileName "filename.html";StringBuilder sb new StringBuilder();// 使用StringBuilder 构建HTML文件sb.append("<html>\n");sb.append("<head>\n");sb.append("<title>HTML File</title>\n");sb.a…...

华为OD机试用Python实现 -【微服务的集成测试】(2023-Q1 新题)
华为OD机试300题大纲 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 华为OD详细说明:https://dream.blog.csdn.net/article/details/128980730 微服务的集成测试…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

