当前位置： 首页 > news >正文

NIO简单介绍

news 2026/2/10 3:15:24

一、什么是NIO

1、Java NIO全称java non-blocking IO， 是指JDK提供的新API。从JDK1.4开始，Java提供了一系列改进的输入/输出的新特性，被统称为NIO(即New IO)，是同步非阻塞的

2、NIO有三大核心部分: Channel(通道)， Buffer(缓冲区),Selector(选择器)

3、NIO是面向缓冲区，或者面向块编程的。数据读取到一个它稍后处理的缓冲区，需要时可在缓冲区中前后移动，这就增加了处理过程中的灵活性，使用它可以提供非阻塞式的高伸缩性网络。

二、NIO 与BIO 模型对比

BIO 是同步阻塞IO,服务器的模式是一个线程处理一个请求，当无响应时，会阻塞线程

NIO 同步非阻塞IO,会有一个Selector管理多个线程，当有事件发生后，进行处理、不会发生阻塞

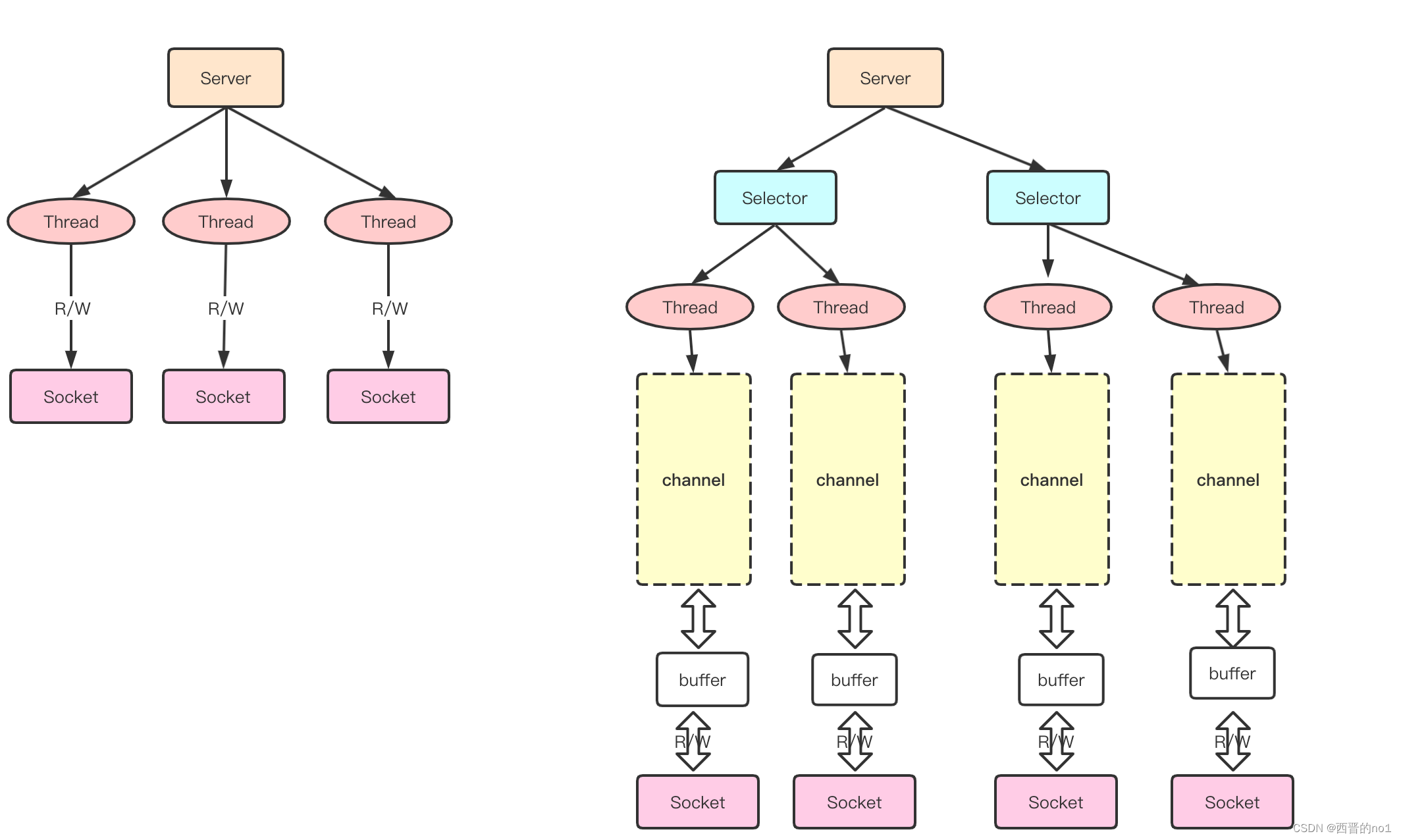
三、NIO 与BIO的差异

1、BIO 以流的方式处理数据,而NIO以块的方式处理数据,块I/O 的效率比流I/O高很多

2、BIO 是阻塞的，NIO则是非阻塞的

3、BIO基 于字节流和字符流进行操作，而NIO 基于Channel(通道)和Buffer(缓冲区)进行操作，数据总是从通道读取到缓冲区中，或者从缓冲区写入到通道中。Selector(选择器)用于监听多个通道的事件(比如:连接请求，数据到达等)，因此使用单个线程就可以监听多个客户端通道

相关文章：

NIO简单介绍

一、什么是NIO 1、Java NIO全称java non-blocking IO， 是指JDK提供的新API。从JDK1.4开始，Java提供了一系列改进的输入/输出的新特性，被统称为NIO(即New IO)，是同步非阻塞的 2、NIO有三大核心部分: Channel(通道)， Buf…...

编程日记 2023/9/24 4:52:47

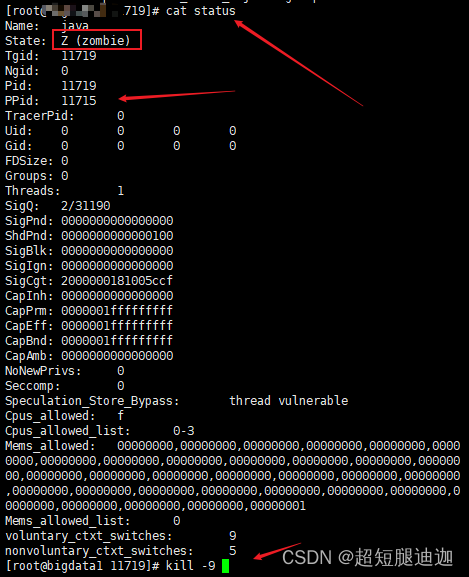
linux进程杀不死

项目场景： 虚拟机 问题描述 linux进程杀不死 无反应 原因分析： 进程僵死zombie 解决方案： 进proc或者find命令找到进程所在地址 cat status查看进程杀死子进程...

编程日记 2023/9/24 4:51:46

5分钟带你搞懂RPA到底是什么？RPA能做什么？

一、RPA的定义 RPA，全称Robotic Process Automation，即机器人流程自动化，是一种软件解决方案，能够模拟人类在计算机上执行的操作，以实现重复性、繁琐任务的自动化。它与传统的计算机自动化有所不同，因为它…...

编程日记 2023/9/24 4:48:43

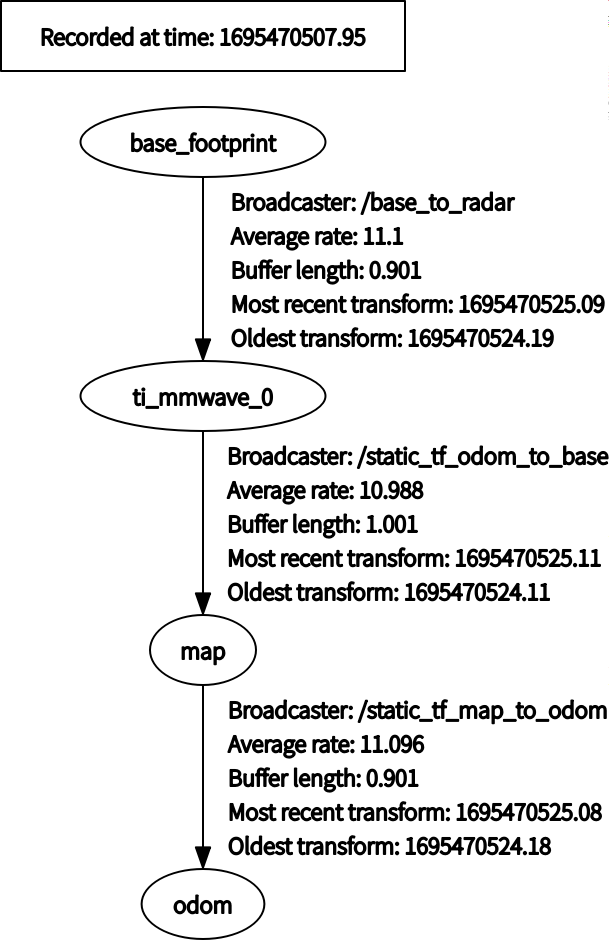
毫米波雷达 TI IWR1443 在 ROS 中进行 octomap 建图

个人实验记录 /mmwave_ti_ros/ros_driver/src/ti_mmwave_rospkg/launch/1443_multi_3d_0.launch <launch><!-- Input arguments --><arg name"device" value"1443" doc"TI mmWave sensor device type [1443, 1642]"/><arg…...

编程日记 2023/9/24 4:47:42

113双周赛

题目列表 2855. 使数组成为递增数组的最少右移次数 2856. 删除数对后的最小数组长度 2857. 统计距离为 k 的点对 2858. 可以到达每一个节点的最少边反转次数 一、使数组成为递增数组的最少右移次数 这题可以直接暴力求解&#xff0c;枚举出每种右移后的数组&#xff0c;将…...

编程日记 2023/9/24 4:45:40

React 全栈体系（九）

第五章 React 路由 一、相关理解 1. SPA 的理解 单页 Web 应用&#xff08;single page web application&#xff0c;SPA&#xff09;。整个应用只有一个完整的页面。点击页面中的链接不会刷新页面&#xff0c;只会做页面的局部更新。数据都需要通过 ajax 请求获取, 并在前端…...

编程日记 2023/9/24 4:44:39

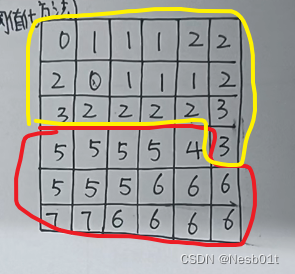
阈值化分割，对灰度级图像进行二值化处理（数字图像处理大题复习 P8）

文章目录 画出表格求出灰度直方图 & 山谷画出结果图 画出表格 有几个0就写几&#xff0c;有几个1就写几&#xff0c;如图 求出灰度直方图 & 山谷 跟前面求灰度直方图的方法一样&#xff0c;找出谷底&#xff0c;发现结果为 4 画出结果图 最终的结果就是&#xf…...

编程日记 2023/9/24 4:43:39

vue3中withDefaults是什么

问: const props withDefaults(defineProps<{// 数据列表lotteryList: { pic: string; name?: string }[];// 中奖idwinId: number;// 抽奖初始转动速度initSpeed: number;// 抽奖最快转动速度fastSpeed: number;// 抽奖最慢转动速度slowSpeed: number;// 基本圈数baseCi…...

编程日记 2023/9/24 4:40:36

Android进阶之路 - 盈利、亏损金额格式化

在金融类型的app中&#xff0c;关于金额、数字都相对敏感和常见一些&#xff0c;在此仅记录我在金融行业期间学到的皮毛&#xff0c;如后续遇到新的场景也会加入该篇 该篇大多采用 Kotlin 扩展函数的方式进行记录&#xff0c;尽可能熟悉 Kotlin 基础知识 兄弟 Blog StringUti…...

编程日记 2023/9/24 4:38:35

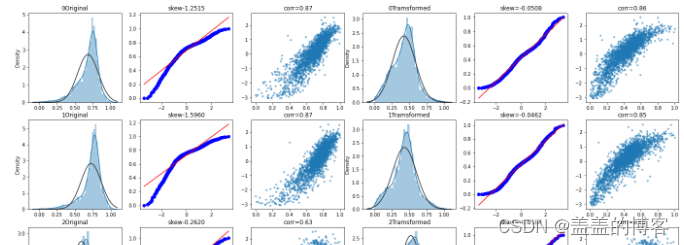
工业蒸汽量预测（速通一）

工业蒸汽量预测&#xff08;一&#xff09; 赛题理解1、评估指标2、赛题模型3、解题思路 理论知识1、变量识别2、变量分析3、缺失值处理4、异常值处理5、变量转换6、新变量生成 数据探索1、导包2、读取数据3、查看数据4、可视化数据分布4.1箱型图4.2获取异常数据并画图4.3直方图…...

编程日记 2023/9/24 4:37:34

机器学习的主要内容

分类任务 回归任务 有一些算法只能解决回归问题有一些算法只能解决分类问题有一些算法的思路既能解决回归问题&#xff0c;又能解决分类问题 一些情况下&#xff0c; 回归任务可以转化为分类任务&#xff0c; 比如我们预测学生的成绩&#xff0c;然后根据学生的成绩划分为A类、…...

编程日记 2023/9/24 4:36:33

华为OD机试真题-分积木-2023年OD统一考试（B卷）

题目描述： Solo和koko是两兄弟，妈妈给了他们一大堆积木，每块积木上都有自己的重量。现在他们想要将这些积木分成两堆。哥哥Solo负责分配，弟弟koko要求两个人获得的积木总重量“相等”（根据Koko的逻辑），个数可以不同，不然就会哭，但koko只会先将两个数转成二进制再进行加…...

编程日记 2023/9/24 4:35:32

SpringBoot自动装配原理及分析

一、什么是自动装配 在使用SpringBoot的时候&#xff0c;会自动将Bean装配到IoC容器中。例如我们在使用Redis数据库的时候&#xff0c;会引入依赖spring-boot-starter-data-redis。在引入这个依赖后&#xff0c;服务初始化的时候&#xff0c;会将操作Redis需要的组件注入到IoC…...

编程日记 2023/9/24 4:34:31

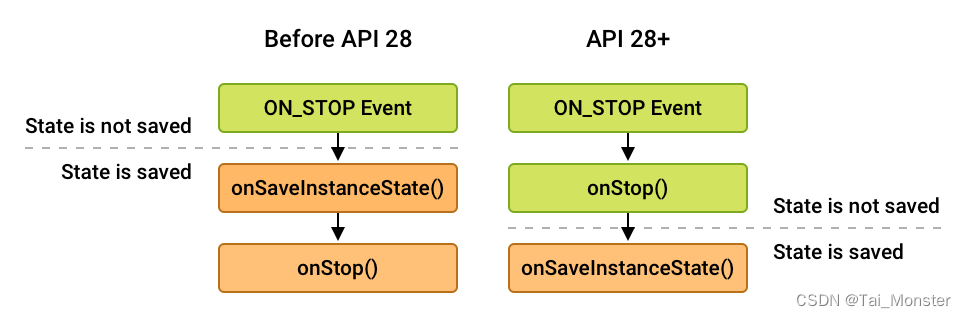
Android开发笔记 ：理解Fragment

Android开发笔记&#xff1a;理解Fragment 导言 本篇文章产生的原因很简单&#xff0c;就是我在了解Android Jetpack中的Lifecycle框架时发现Lifecycle具体时间和状态的更新都是由一个名为ReportFragment的Fragment来跟踪的&#xff0c;为了更好的了解Fragment是如何追踪Activ…...

编程日记 2023/9/24 4:31:28

std::chrono获取当前秒级/毫秒级/微秒级/纳秒级时间戳

当前时间戳获取方法 先使用std::chrono获取当前系统时间&#xff0c;然后将当前系统时间转换为纪元时间std::time_t类型&#xff0c;之后使用std::localtime对std::time_t类型转换为本地时间结构体std::tm类型&#xff0c;最后使用strftime对时间进行格式化输出。 其中std::t…...

编程日记 2023/9/24 4:28:26

sh文件介绍及linux下执行

Shell脚本是一种用于自动化任务和系统管理的脚本语言。它允许用户通过命令行界面执行一系列命令&#xff0c;从而简化了重复性任务的处理过程。 以下是关于Shell脚本的一些基本概念&#xff1a; 1. Shell脚本通常以“.sh”扩展名保存&#xff0c;例如“script.sh”。 2. Shell…...

编程日记 2023/9/24 4:26:23

js-cookie使用 js深度克隆（判断引用类型是数组还是对象的方法）

cookie和深度拷贝的使用 1、js-cookie使用2、js深度克隆 1、js-cookie使用 前端的本地存储分为 localstorage、sesstionstorage、cookie 但是咱们有时候需要做7天免登录的需求时&#xff0c;选择 cookie 作为前端的本地存储是在合适不过的了 直接操作 cookie 可以&#xff0c; …...

编程日记 2023/9/24 4:24:22

[Pytorch]语义分割任务分类的实现

文章目录 [Pytorch]语义分割任务分类的实现 [Pytorch]语义分割任务分类的实现 假如我们定义了一个网络用于语义分割任务&#xff0c;这个网络简称为model() 语义分割任务要做的是&#xff1a; 对于一个图片输入input&#xff0c;大小为&#xff08;B&#xff0c;C&#xff0c…...

编程日记 2023/9/24 4:22:20

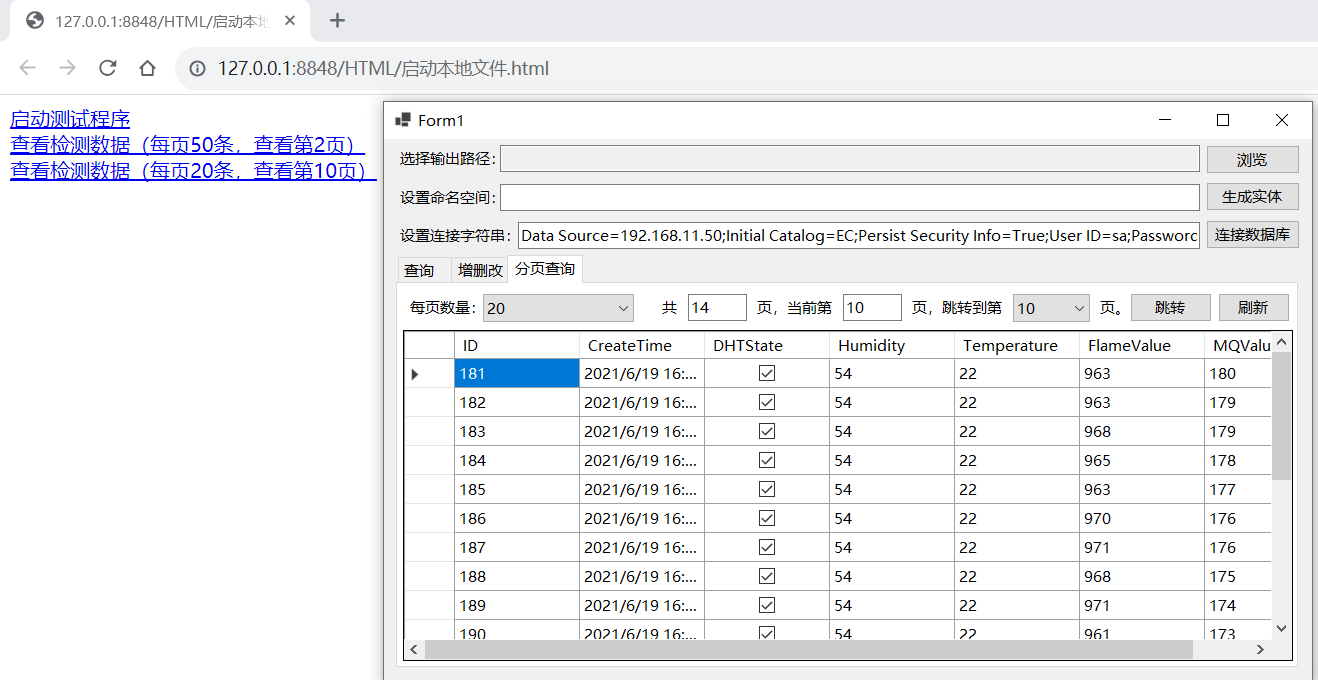
测试网页调用本地可执行程序（续：带参数调用）

前篇文章介绍了网页调用本地可执行程序的方式&#xff0c;通过在注册表中注册命令&#xff0c;然后在网页中调用命令启动本地程序。如果需要传递参数&#xff0c;则需要在注册表命令中的command项中设置如下形式的值。 "XXXXXX\XXXXXXX.exe" "%1"&emsp…...

编程日记 2023/9/24 4:21:19

Carla自动驾驶模拟器安装和使用

Carla自动驾驶模拟器安装和使用 1 安装 ubuntu20.04安装carla0.9.11版本 步骤1&#xff1a;打开下面链接&#xff0c;点击第一个[Ubuntu] CARLA_0.9.11.tar.gz carla-0.9.11源码下载 步骤2&#xff1a;下载完解压到/opt目录下 我的话是先在下载目录上提取解压&#xff0c;然…...

编程日记 2023/9/24 4:18:16

＜6＞-MySQL表的增删查改

目录 一&#xff0c;create&#xff08;创建表&#xff09; 二&#xff0c;retrieve&#xff08;查询表&#xff09; 1&#xff0c;select列 2&#xff0c;where条件 三&#xff0c;update&#xff08;更新表&#xff09; 四&#xff0c;delete&#xff08;删除表&#xf…...

编程新知 2025/12/11 18:28:17

AI Agent与Agentic AI：原理、应用、挑战与未来展望

文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例&#xff1a;使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例&#xff1a;使用OpenAI GPT-3进…...

编程新知 2026/1/23 7:04:53

Opencv中的addweighted函数

一.addweighted函数作用 addweighted&#xff08;&#xff09;是OpenCV库中用于图像处理的函数&#xff0c;主要功能是将两个输入图像&#xff08;尺寸和类型相同&#xff09;按照指定的权重进行加权叠加&#xff08;图像融合&#xff09;&#xff0c;并添加一个标量值&#x…...

编程新知 2026/2/1 1:50:03

C++.OpenGL （10/64）基础光照（Basic Lighting）

基础光照（Basic Lighting） 冯氏光照模型（Phong Lighting Model） #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

编程新知 2026/1/20 2:37:04

如何理解 IP 数据报中的 TTL？

目录 前言理解 前言 面试灵魂一问&#xff1a;说说对 IP 数据报中 TTL 的理解&#xff1f;我们都知道&#xff0c;IP 数据报由首部和数据两部分组成&#xff0c;首部又分为两部分&#xff1a;固定部分和可变部分&#xff0c;共占 20 字节&#xff0c;而即将讨论的 TTL 就位于首…...

编程新知 2026/2/4 18:09:49

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波（Mean Shift Filtering）函数meanShiftFiltering()

操作系统&#xff1a;ubuntu22.04 OpenCV版本&#xff1a;OpenCV4.9 IDE:Visual Studio Code 编程语言&#xff1a;C11 算法描述 在 GPU 上对图像执行 均值漂移滤波&#xff08;Mean Shift Filtering&#xff09;&#xff0c;用于图像分割或平滑处理。 该函数将输入图像中的…...

编程新知 2026/1/20 12:53:30

AI书签管理工具开发全记录（十九）：嵌入资源处理

1.前言 &#x1f4dd; 在上一篇文章中&#xff0c;我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源&#xff0c;方便后续将资源打包到一个可执行文件中。 2.embed介绍 &#x1f3af; Go 1.16 引入了革命性的 embed 包&#xff0c;彻底改变了静态资源管理的…...

编程新知 2026/1/30 16:24:23

企业如何增强终端安全？

在数字化转型加速的今天&#xff0c;企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机&#xff0c;到工厂里的物联网设备、智能传感器&#xff0c;这些终端构成了企业与外部世界连接的 “神经末梢”。然而&#xff0c;随着远程办公的常态化和设备接入的爆炸式…...

编程新知 2026/1/29 9:14:58

Redis的发布订阅模式与专业的 MQ（如 Kafka, RabbitMQ）相比，优缺点是什么？适用于哪些场景？

Redis 的发布订阅&#xff08;Pub/Sub&#xff09;模式与专业的 MQ&#xff08;Message Queue&#xff09;如 Kafka、RabbitMQ 进行比较&#xff0c;核心的权衡点在于&#xff1a;简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

编程新知 2025/12/4 2:32:37

排序算法总结（C++）

目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指&#xff1a;同样大小的样本 **&#xff08;同样大小的数据&#xff09;**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

编程新知 2026/1/25 9:33:23