深度学习自学笔记二:逻辑回归和梯度下降法
目录
一、逻辑回归
二、逻辑回归的代价函数
三、梯度下降法
一、逻辑回归
逻辑回归是一种常用的二分类算法,用于将输入数据映射到一个概率输出,表示为属于某个类别的概率。它基于线性回归模型,并使用了sigmoid函数作为激活函数。
假设我们有一个二分类问题,其中输入特征为x,对应的样本标签为y(0或1)。逻辑回归的目标是根据输入特征x预测样本标签y的概率。
逻辑回归模型可以表示为:
z = w * x + b
其中,w是权重向量,x是输入特征向量,b是偏置。这部分与线性回归模型相似。
不同之处在于,逻辑回归模型还引入了一个sigmoid函数(也称为逻辑函数)g(z),用于将线性模型的输出z映射到0和1之间的概率值。sigmoid函数的数学表达式如下:
g(z) = 1 / (1 + e^(-z))
通过将线性模型的输出z传入sigmoid函数,得到的结果g(z)表示样本属于正类的概率。反之,1 - g(z)表示样本属于负类的概率。
在训练阶段,我们需要通过最大似然估计或者梯度下降等优化方法来找到最优的权重向量w和偏置b,使得模型的预测结果与实际标签尽可能地接近。
训练过程中的损失函数通常采用交叉熵损失(cross-entropy loss),它可以衡量实际概率分布与预测概率分布之间的差异。通过最小化损失函数,我们可以更新权重向量w和偏置b,以提高模型的预测准确性。
在预测阶段,给定新的输入特征x,我们可以使用训练好的权重向量w和偏置b,将其代入逻辑回归模型,并通过sigmoid函数计算输出概率g(z)。一般而言,如果g(z)大于等于0.5,则我们将样本预测为正类;如果g(z)小于0.5,则预测为负类。
二、逻辑回归的代价函数
逻辑回归模型的代价函数(Cost Function)通常使用交叉熵损失函数(Cross-Entropy Loss)来衡量实际概率分布与模型预测概率分布之间的差异。
假设我们有一个训练集包含m个样本,每个样本的输入特征为x,对应的真实标签为y(0或1)。逻辑回归的目标是找到最优的权重向量w和偏置b,使得模型的预测结果尽可能接近真实标签。
对于每个样本i,逻辑回归模型的预测值表示为y_hat_i,它是通过将输入特征x_i代入逻辑回归模型中计算得到的。预测值y_hat_i可以看作样本i属于正类的概率。
交叉熵损失函数的数学表达式如下:
J(w, b) = - (1/m) * Σ(y_i * log(y_hat_i) + (1-y_i) * log(1-y_hat_i))
其中,J(w, b)表示代价函数,w和b表示权重向量和偏置,m表示样本数量,y_i表示第i个样本的真实标签,y_hat_i表示对应的预测值。
交叉熵损失函数由两部分组成。当真实标签y_i为1时,第一部分y_i * log(y_hat_i)用于衡量模型对正类样本的预测准确性。当真实标签y_i为0时,第二部分(1-y_i) * log(1-y_hat_i)用于衡量模型对负类样本的预测准确性。
代价函数J(w, b)可以看作是对所有样本的预测误差进行平均后取反的结果。我们的目标是通过最小化代价函数来找到最优的权重向量w和偏置b,使得模型的预测结果与真实标签尽可能接近。
在训练阶段,通常使用梯度下降等优化算法来更新权重向量w和偏置b,以最小化代价函数。通过不断迭代优化,逻辑回归模型能够逐渐提高对样本标签的预测准确性。
三、梯度下降法
梯度下降法(Gradient Descent)是一种常用的优化算法,用于最小化代价函数(Cost Function)或损失函数。在逻辑回归等机器学习模型中,梯度下降法常用于更新模型参数,以找到使代价函数最小化的权重和偏置。
梯度下降法的基本思想是通过迭代更新参数,沿着代价函数的负梯度方向移动,以逐步接近代价函数的最小值。具体而言,梯度下降法包括以下步骤:
1. 初始化参数:将权重向量w和偏置b初始化为任意值。
2. 计算梯度:对于每个参数,计算代价函数关于该参数的偏导数(梯度)。这可以使用链式法则来计算,根据代价函数的形式不同而有所不同。
3. 更新参数:根据梯度的方向和学习率(learning rate),更新参数的值。学习率决定了每次参数更新的步长,较大的学习率可能导致无法收敛,而较小的学习率可能导致收敛速度过慢。
4. 重复步骤2和3:重复计算梯度和更新参数的过程,直到达到停止条件。停止条件可以是达到一定的迭代次数,或者代价函数的变化小于某个阈值等。
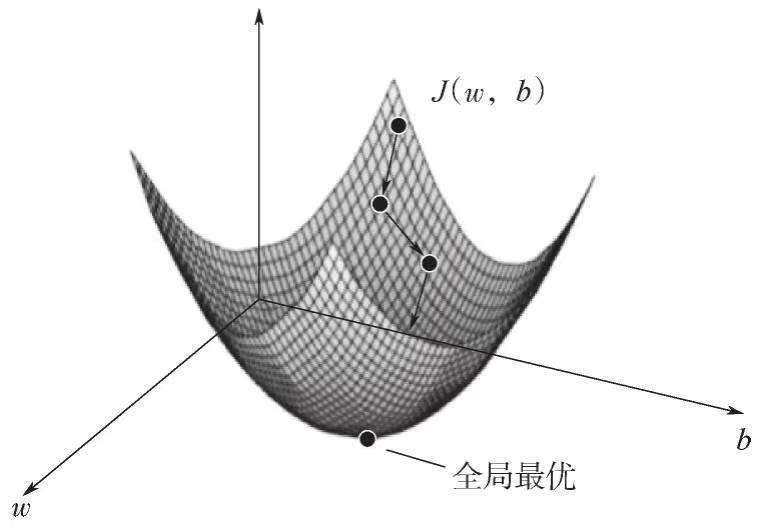
添加图片注释,不超过 140 字(可选)
在逻辑回归中,梯度下降法的目标是最小化代价函数。通过不断更新权重向量w和偏置b,使得模型的预测结果与真实标签尽可能接近。通过迭代优化过程,梯度下降法可以找到局部最优解或接近最优解的参数值,从而提高模型的准确性。
需要注意的是,梯度下降法有多种变体,例如批量梯度下降(Batch Gradient Descent)、随机梯度下降(Stochastic Gradient Descent)和小批量梯度下降(Mini-Batch Gradient Descent)。它们的区别在于每次更新参数时使用的样本数量。批量梯度下降使用整个训练集,随机梯度下降使用单个样本,而小批量梯度下降使用一小部分样本来计算梯度和更新参数。不同的变体在收敛速度和计算效率上可能会有所差异。
相关文章:

深度学习自学笔记二:逻辑回归和梯度下降法
目录 一、逻辑回归 二、逻辑回归的代价函数 三、梯度下降法 一、逻辑回归 逻辑回归是一种常用的二分类算法,用于将输入数据映射到一个概率输出,表示为属于某个类别的概率。它基于线性回归模型,并使用了sigmoid函数作为激活函数。 假设我们…...
【Element】通知 Notification
ElementUI 弹出通知 created() {const h this.$createElementconst that thisthis.$notify({onClose: function () {that.do()},type: warning,duration: 5000, // 5秒后隐藏offset: 0, // 距离顶部dangerouslyUseHTMLString: false, showClose: false,customClass: notify-…...
vue+express、gitee pm2部署轻量服务器(20230923)
一、代码配置 前后端接口都保持 127.0.0.1:3000 vue 项目 创建文件 pm2.config.cjs module.exports {apps: [{name: xin-web, // 应用程序的名称script: npm, // 启动脚本args: run dev, // 启动脚本的参数cwd: /home/vue/xin_web, // Vite 项目的根目录interpreter: none,…...

前端教程-H5游戏开发
Egret EGRETIA RC 版本正式发布 从端到云一站式区块链游戏开发工作流 官网 Laya Air 在渲染模式上,LayaAir 支持 Canvas 和 WebGL 两种方式;在工具流的支持程度上,主要是提供了 LayaAir IDE。LayaAir IDE 包括代码模式与设计模式ÿ…...
Nginx 关闭/屏蔽 PUT、DELETE、OPTIONS 请求
1、修改 nginx 配置 在 nginx 配置文件中,增加如下配置内容: if ($request_method !~* GET|POST|HEAD) {return 403; }修改效果如下: 2、重启 nginx 服务 systemctl restart nginx或者 service nginx restart3、功能验证 使用如下方式…...

【React】React概念、特点和Jsx基础语法
React是什么? React 是一个用于构建用户界面的 JavaScript 库。 是一个将数据渲染为 HTML 视图的开源 JS 库它遵循基于组件的方法,有助于构建可重用的 UI 组件它用于开发复杂的交互式的 web 和移动 UI React有什么特点 使用虚拟 DOM 而不是真正的 DO…...

大数据的崭露头角:数据湖与数据仓库的融合之道
文章目录 数据湖与数据仓库的基本概念数据湖(Data Lake)数据仓库(Data Warehouse) 数据湖和数据仓库的优势和劣势数据湖的优势数据湖的劣势数据仓库的优势数据仓库的劣势 数据湖与数据仓库的融合之道1. 数据分类和标记2. 元数据管…...

用go实现cors中间件
目录 一、概述 二、简单请求和预检请求 简单请求 预检请求 三、使用go的gin框架实现cors配置 1、安装 2、函数 一、概述 CORS(Cross-Origin Resource Sharing)是一种浏览器安全机制,用于控制在Web应用程序中不同源(Origin&a…...
Linux 链表示例 LIST_INIT LIST_INSERT_HEAD
list(3) — Linux manual page 用Visual Studio 2022创建CMake项目 * CmakeLists.txt # CMakeList.txt : Top-level CMake project file, do global configuration # and include sub-projects here. # cmake_minimum_required (VERSION 3.12)project ("llist")# I…...
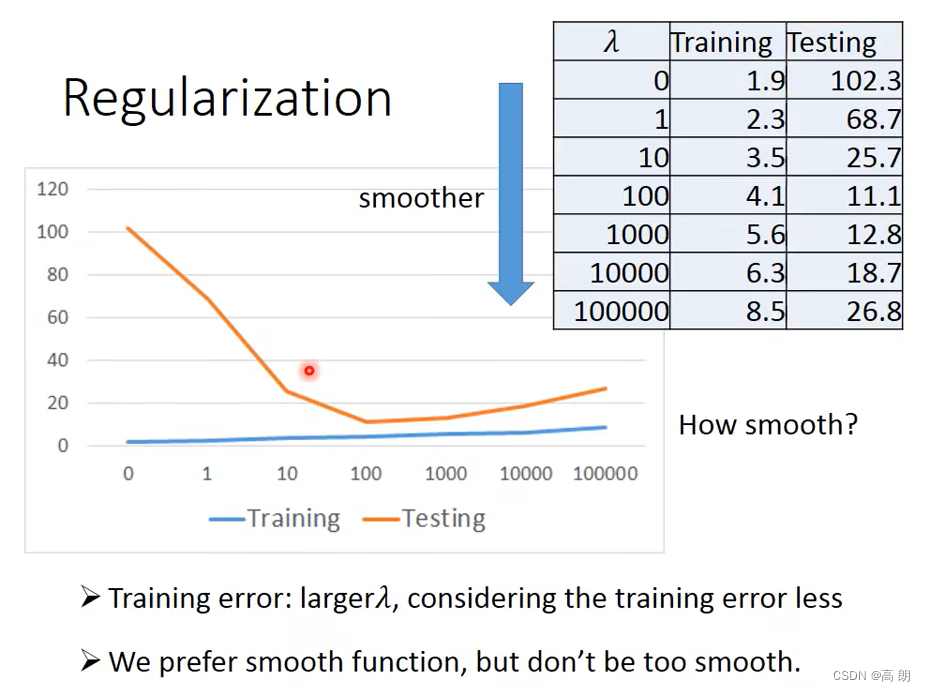
【机器学习】详解回归(Regression)
文章目录 是什么的问题案例说明 是什么的问题 回归分析(Regression Analysis) 是研究自变量与因变量之间数量变化关系的一种分析方法,它主要是通过因变量Y与影响它的自变量 X i ( i 1 , 2 , 3 … ) X_i(i1…...
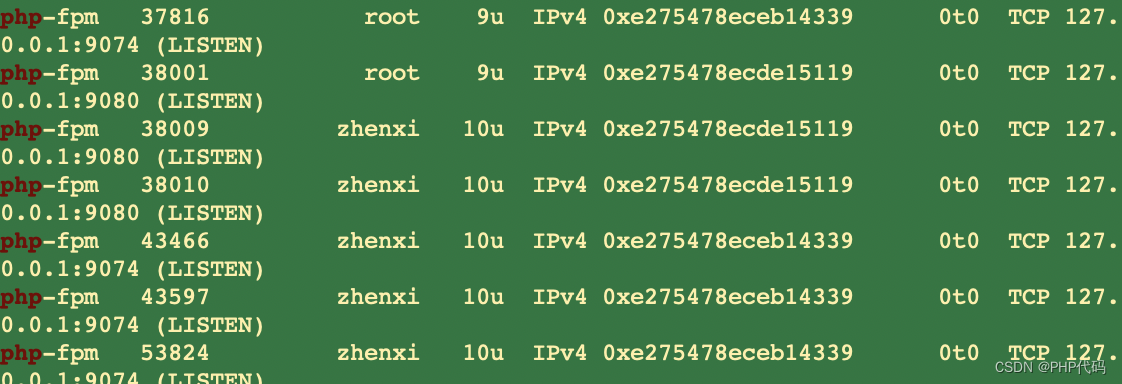
mac 配置 httpd nginx php-fpm 详细记录 已解决
在日常mac电脑 开发php项目一直是 httpd 方式 运行,由于有 多版本 运行的需求,docker不想用,索性用 php-fpm进行 功能处理。上次配置 是好的,但是感觉马马虎虎,这次 配置底朝天。因为配置服务器,几乎也都是…...

Angular 项目升级需要注意什么?
升级Angular项目是一个重要的任务,因为它可以帮助你获得新的功能、性能改进和安全性增强。然而,Angular的版本升级可能会涉及到一些潜在的问题和挑战。以下是升级Angular项目时需要注意的一些重要事项: 备份项目:在升级之前&…...

开发高性能知识付费平台:关键技术策略
引言 在构建知识付费平台时,高性能是确保用户满意度和平台成功的关键因素之一。本文将探讨一些关键的技术策略,帮助开发者打造高性能的知识付费平台。 1. 前端性能优化 使用CDN加速资源加载 使用内容分发网络(CDN)来托管和加…...

python图像匹配:如何使用Python进行图像匹配
Python图像匹配是指使用Python编写的程序来进行图像匹配。它可以在两幅图像之间找到相似的部分,从而实现图像检索、图像比较、图像拼接等功能。 Python图像匹配是指使用Python编写的程序来进行图像匹配。它可以在两幅图像之间找到相似的部分,从而实现图…...
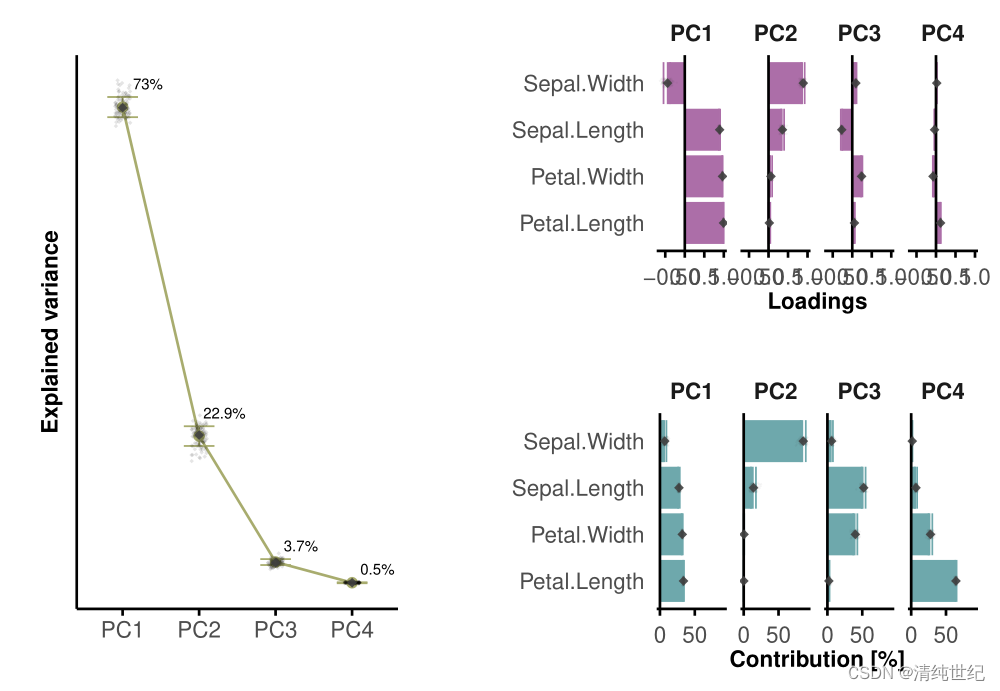
R语言绘制PCA双标图、碎石图、变量载荷图和变量贡献图
1、原论文数据双标图 代码: setwd("D:/Desktop/0000/R") #更改路径#导入数据 df <- read.table("Input data.csv", header T, sep ",")# ----------------------------------- #所需的包: packages <- c("ggplot2&quo…...
)
Jolokia 笔记 (Kafka/start/stop)
目录 1. Jolokia 笔记 (Kafka/start/stop) 1. Jolokia 笔记 (Kafka/start/stop) java -javaagent:agent.jarport8778,hostlocalhostJolokia 是作为 Kafka 的 Java agent, 基于 HTTP 协议提供了一个使用 JSON 作为数据格式的外部接口, 提供给 DataKit 使用。 Kafka 启动时, 先配…...
Qt5开发及实例V2.0-第十九章-Qt.QML编程基础
Qt5开发及实例V2.0-第十九章-Qt.QML编程基础 第19章 QML编程基础19.1 QML概述19.1.1 第一个QML程序19.1.2 QML文档构成19.1.3 QML基本语法 19.2 QML可视元素19.2.1 Rectangle(矩形)元素19.2.2 Image(图像)元素19.2.3 Text…...

固定开发板的ifconfig的IP地址
背景 由于我是使用vsocode的ssh插件远程连接我的开发板, 所以我每次开机就要重新连上屏幕看一下这个ifconfig的ip地址然后更改我的ssh config文件 这里提供一个使用nmcli设置静态IP的方法 请确保使用你的实际连接名称替换Wi-Fi connection 1 使用nmcli设置静态IP相对直接&a…...

停车场系统源码
源码下载地址(小程序开源地址):停车场系统小程序,新能源电动车充电系统,智慧社区物业人脸门禁小程序: 【涵盖内容】:城市智慧停车系统,汽车新能源充电,两轮电动车充电,物…...

R语言贝叶斯MCMC:GLM逻辑回归、Rstan线性回归、Metropolis Hastings与Gibbs采样算法实例...
原文链接:http://tecdat.cn/?p23236 在频率学派中,观察样本是随机的,而参数是固定的、未知的数量(点击文末“阅读原文”获取完整代码数据)。 相关视频 什么是频率学派? 概率被解释为一个随机过程的许多观测…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
