怒刷LeetCode的第14天(Java版)
目录
第一题
题目来源
题目内容
解决方法
方法一:动态规划
方法二:栈
方法三:双指针
第二题
题目来源
题目内容
解决方法
方法一:二分查找
方法二:线性扫描
方法三:递归
第三题
题目来源
题目内容
解决方法
方法一:二分查找
方法二:线性扫描
方法三:双指针
第一题
题目来源
32. 最长有效括号 - 力扣(LeetCode)
题目内容

解决方法
方法一:动态规划
- 创建一个长度为
n的数组dp,用于保存以当前字符结尾的最长有效括号子串的长度。 - 初始化
dp数组的所有元素为 0。 - 遍历字符串
s的每个字符:- 如果当前字符是
(,则直接跳过。 - 如果当前字符是
),则判断前一个字符是否是(:- 如果前一个字符是
(,则更新dp[i] = dp[i-2] + 2,表示以当前字符结尾的最长有效括号子串长度为前一个字符结尾的最长有效括号子串长度加上当前的两个括号。 - 如果前一个字符是
),则判断前一个字符结尾的最长有效括号子串之前的字符是否是(,即判断i-dp[i-1]-1位置的字符是否是(:- 如果是
(,则更新dp[i] = dp[i-1] + dp[i-dp[i-1]-2] + 2,表示以当前字符结尾的最长有效括号子串长度为前一个字符结尾的最长有效括号子串长度加上前一个字符结尾的最长有效括号子串之前的最长有效括号子串长度加上当前的两个括号。
- 如果是
- 如果前一个字符是
- 如果当前字符是
- 遍历完整个字符串后,找出
dp数组中的最大值,即为最长有效括号子串的长度。
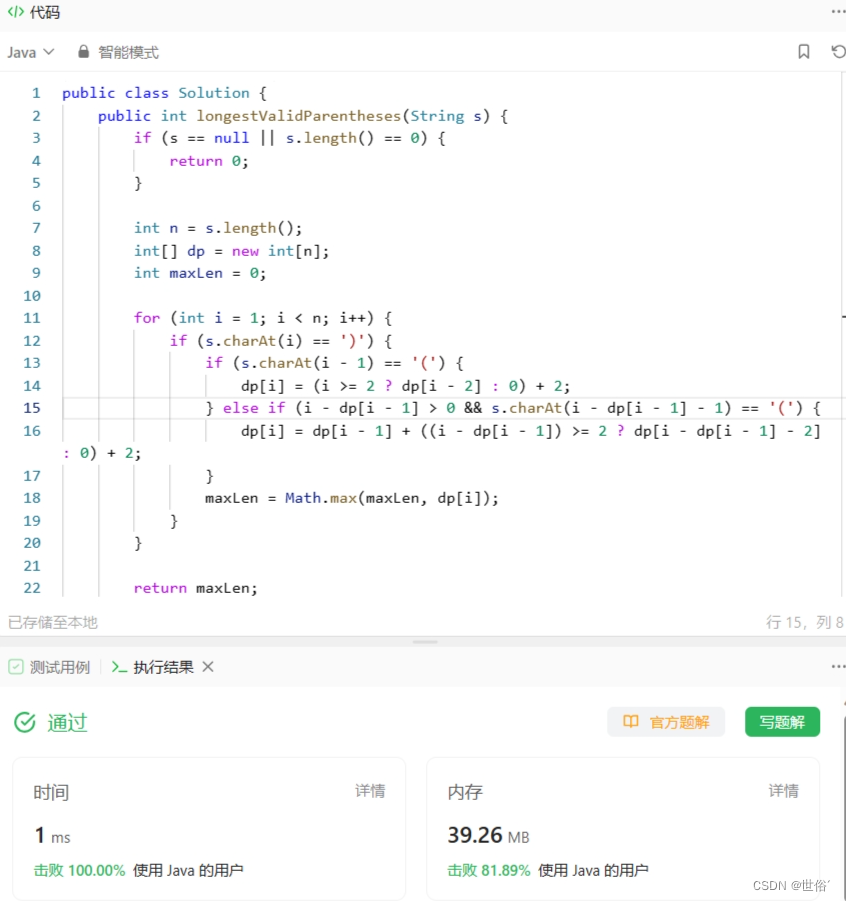
public class Solution {public int longestValidParentheses(String s) {if (s == null || s.length() == 0) {return 0;}int n = s.length();int[] dp = new int[n];int maxLen = 0;for (int i = 1; i < n; i++) {if (s.charAt(i) == ')') {if (s.charAt(i - 1) == '(') {dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;} else if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') {dp[i] = dp[i - 1] + ((i - dp[i - 1]) >= 2 ? dp[i - dp[i - 1] - 2] : 0) + 2;}maxLen = Math.max(maxLen, dp[i]);}}return maxLen;}
}
复杂度分析:
时间复杂度:
- 遍历字符串
s的每个字符需要 O(n) 的时间。 - 在每个字符上,我们都进行了常数次的比较和更新操作。
- 因此,总体上,时间复杂度为 O(n)。
空间复杂度:
- 我们使用了一个长度为
n的数组dp来保存以当前字符结尾的最长有效括号子串的长度。 - 因此,空间复杂度为 O(n)。
综合起来,该解法的时间复杂度为 O(n),空间复杂度为 O(n)。
注意:对于这个特定的问题,在给定的限制条件下(0 <= s.length <= 3 * 10^4),这个解法是高效且可行的。
LeetCode运行结果:
方法二:栈
该方法的思路如下:
- 首先,我们使用一个栈来保存括号的索引位置。
- 初始化栈,将一个特殊的值
-1放入栈中。 - 遍历字符串
s的每个字符:- 如果遇到左括号
(,将其索引位置压入栈中。 - 如果遇到右括号
),弹出栈顶元素,表示当前右括号匹配了一个左括号。- 如果栈为空,将当前右括号的索引位置压入栈中,作为一个新的起点。
- 如果栈不为空,计算当前有效括号子串的长度,更新最大长度。
- 如果遇到左括号
- 最后,返回最大长度即可。
import java.util.Stack;public class Solution {public int longestValidParentheses(String s) {if (s == null || s.length() == 0) {return 0;}int maxLen = 0;Stack<Integer> stack = new Stack<>();stack.push(-1);for (int i = 0; i < s.length(); i++) {char c = s.charAt(i);if (c == '(') {stack.push(i);} else {stack.pop();if (stack.isEmpty()) {stack.push(i);} else {maxLen = Math.max(maxLen, i - stack.peek());}}}return maxLen;}
}
复杂度分析:
时间复杂度:
- 遍历字符串 s 的每个字符需要 O(n) 的时间。
- 在每个字符上,我们进行了常数次的栈操作(压栈和弹栈)。
- 因此,总体上,时间复杂度为 O(n)。
空间复杂度:
- 我们使用了一个栈来保存括号的索引位置。
- 在最坏情况下,当所有字符都是左括号时,栈的大小为 n。
- 因此,空间复杂度为 O(n)。
综合起来,该方法的时间复杂度为 O(n),空间复杂度为 O(n)。
LeetCode运行结果:

方法三:双指针
除了动态规划和栈,还有一种双指针的方法来解决最长有效括号问题。
这种方法的思路如下:
- 从左到右遍历字符串,统计左右括号的数量。
- 如果左右括号数量相等,则更新最大长度。
- 如果右括号数量大于左括号数量,则重置左右括号数量为0。
- 然后从右到左再进行一次相同的操作。
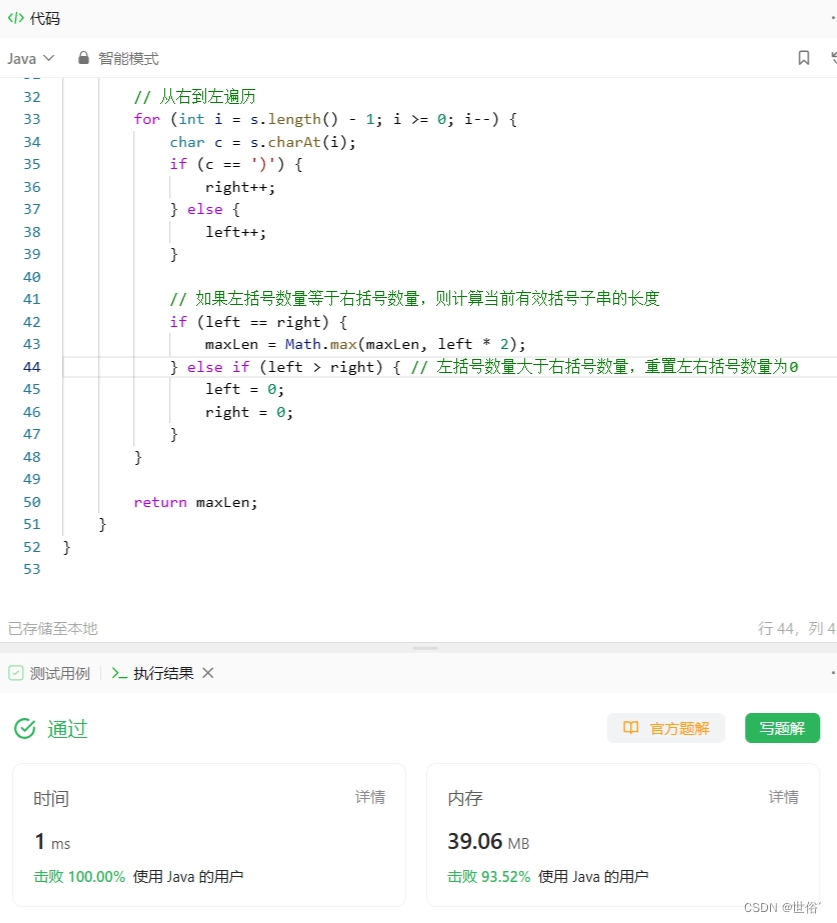
public class Solution {public int longestValidParentheses(String s) {if (s == null || s.length() == 0) {return 0;}int left = 0; // 左括号数量int right = 0; // 右括号数量int maxLen = 0; // 最大长度// 从左到右遍历for (int i = 0; i < s.length(); i++) {char c = s.charAt(i);if (c == '(') {left++;} else {right++;}// 如果左括号数量等于右括号数量,则计算当前有效括号子串的长度if (left == right) {maxLen = Math.max(maxLen, right * 2);} else if (right > left) { // 右括号数量大于左括号数量,重置左右括号数量为0left = 0;right = 0;}}left = 0;right = 0;// 从右到左遍历for (int i = s.length() - 1; i >= 0; i--) {char c = s.charAt(i);if (c == ')') {right++;} else {left++;}// 如果左括号数量等于右括号数量,则计算当前有效括号子串的长度if (left == right) {maxLen = Math.max(maxLen, left * 2);} else if (left > right) { // 左括号数量大于右括号数量,重置左右括号数量为0left = 0;right = 0;}}return maxLen;}
}
复杂度分析:
时间复杂度:
- 遍历字符串 s 的每个字符需要 O(n) 的时间。
- 在第一次从左到右遍历中,我们进行了常数次的操作,不会产生额外的时间复杂度。
- 在第二次从右到左遍历中,同样也进行了常数次的操作。
- 因此,总体上,时间复杂度为 O(n)。
空间复杂度:
- 我们只使用了常数个变量来保存左右括号的数量和最大长度,没有使用额外的数据结构。
- 因此,空间复杂度为 O(1)。
综合起来,该方法的时间复杂度为 O(n),空间复杂度为 O(1)。
LeetCode运行结果:
第二题
题目来源
33. 搜索旋转排序数组 - 力扣(LeetCode)
题目内容

解决方法
方法一:二分查找
使用二分查找的思想,通过判断左右半边哪一边是有序的来决定向哪边继续查找。具体步骤如下:
- 初始化左指针
left为数组的第一个元素的索引,右指针right为数组最后一个元素的索引。 - 在每次循环中,计算中间元素的索引
mid。 - 如果中间元素等于目标值,则返回
mid。 - 判断左半边是否有序(即
nums[left] <= nums[mid]):- 如果目标值在左半边的有序范围内,则将右指针
right移动到mid - 1,继续在左半边查找。 - 否则,将左指针
left移动到mid + 1,继续在右半边查找。
- 如果目标值在左半边的有序范围内,则将右指针
- 如果左半边不是有序的,则右半边一定是有序的。判断目标值是否在右半边的有序范围内:
- 如果是,则将左指针
left移动到mid + 1,继续在右半边查找。 - 否则,将右指针
right移动到mid - 1,继续在左半边查找。
- 如果是,则将左指针
- 如果循环结束仍未找到目标值,则返回 -1。
public class Solution {public int search(int[] nums, int target) {if (nums == null || nums.length == 0) {return -1;}int left = 0;int right = nums.length - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] == target) {return mid;}if (nums[left] <= nums[mid]) { // 左半边有序if (target >= nums[left] && target < nums[mid]) {right = mid - 1;} else {left = mid + 1;}} else { // 右半边有序if (target > nums[mid] && target <= nums[right]) {left = mid + 1;} else {right = mid - 1;}}}return -1;}
}
复杂度分析:
- 该算法的时间复杂度为O(log n),其中n是数组的长度。在每次循环中,都将搜索范围缩小一半,所以总共最多需要进行log n次循环。因此,算法的时间复杂度为O(log n)。
- 空间复杂度为O(1),因为算法只使用了有限的额外空间来存储指针和常量。
总结起来,该算法具有较低的时间复杂度和空间复杂度,能够高效地解决搜索旋转排序数组的问题。
LeetCode运行结果:

方法二:线性扫描
除了二分查找的方法,还可以使用线性扫描的方法来搜索旋转排序数组。
该算法从数组的第一个元素开始,依次遍历数组中的每个元素,如果找到目标值,则返回其索引;如果遍历结束仍未找到目标值,则返回-1。
public class Solution {public int search(int[] nums, int target) {if (nums == null || nums.length == 0) {return -1;}for (int i = 0; i < nums.length; i++) {if (nums[i] == target) {return i;}}return -1;}
}
复杂度分析:
- 线性扫描算法的时间复杂度为O(n),其中n是数组的长度。算法需要遍历整个数组来查找目标值,因此最坏情况下需要执行n次比较操作。
- 空间复杂度为O(1),因为算法没有使用额外的空间,只需常数级别的额外空间。
相对于二分查找算法的O(log n)时间复杂度,线性扫描算法的时间复杂度较高。但在某些特定场景或者输入规模较小的情况下,线性扫描算法也可以快速解决问题。
综上所述,线性扫描算法适用于简单的问题或者规模较小的数据集,但在更大规模的数据集上,二分查找算法通常更具优势。
LeetCode运行结果:

方法三:递归
除了二分查找和线性扫描的方法,还可以使用递归的方法来搜索旋转排序数组。
该算法与二分查找算法类似,也是通过判断左右半边哪一边是有序的来决定向哪边继续查找。不同之处在于,该算法使用递归的方式实现,将数组的搜索范围不断缩小。
- 算法首先检查数组是否为空或者长度为0,如果是,则返回-1。然后调用递归函数 search 进行搜索,传入参数 nums 数组、目标值 target、搜索范围的左右端点索引 left 和 right。
- 在递归函数中,首先判断搜索范围是否合法,如果不合法,则返回-1。然后计算中间元素索引 mid。如果中间元素等于目标值,则返回 mid。
- 接着判断左半边是否有序(即 nums[left] <= nums[mid])。如果是,则判断目标值是否在左半边的有序范围内。如果是,则继续在左半边递归查找;否则,在右半边递归查找。
- 如果左半边不是有序的,则右半边一定是有序的。判断目标值是否在右半边的有序范围内。如果是,则在右半边递归查找;否则,在左半边递归查找。
- 最后,如果循环结束仍未找到目标值,则返回-1。
public class Solution {public int search(int[] nums, int target) {if (nums == null || nums.length == 0) {return -1;}return search(nums, target, 0, nums.length - 1);}private int search(int[] nums, int target, int left, int right) {if (left > right) {return -1;}int mid = left + (right - left) / 2;if (nums[mid] == target) {return mid;}if (nums[left] <= nums[mid]) { // 左半边有序if (target >= nums[left] && target < nums[mid]) {return search(nums, target, left, mid - 1);} else {return search(nums, target, mid + 1, right);}} else { // 右半边有序if (target > nums[mid] && target <= nums[right]) {return search(nums, target, mid + 1, right);} else {return search(nums, target, left, mid - 1);}}}
}
复杂度分析:
时间复杂度:
- 最好情况下,数组是完全有序的,每次都能通过比较找到目标值,时间复杂度为 O(log n)。
- 最坏情况下,每次都只能排除一个元素,需要遍历整个数组,时间复杂度为 O(n)。
- 平均情况下,假设数组中大致一半是有序的,一半是无序的,时间复杂度介于 O(log n) 和 O(n) 之间。
空间复杂度:
- 每次递归调用会在栈上保存一些临时变量和返回地址,最大递归深度为 log n,因此空间复杂度为 O(log n)。
综合考虑,递归搜索旋转排序数组的算法在最坏情况下的时间复杂度为 O(n),空间复杂度为 O(log n)。但如果数组是近似有序的或者目标值位于有序部分内,时间复杂度可以接近 O(log n),效率较高。
需要注意的是,递归算法和二分查找算法类似,但由于需要额外的栈空间,因此可能会更慢。在处理超大规模数据时,可能会导致栈溢出问题。
LeetCode运行结果:

第三题
题目来源
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
题目内容

解决方法
方法一:二分查找
- 首先,我们定义一个长度为2的整数数组 result,并初始化为 {-1, -1}。这个数组表示目标值的开始位置和结束位置。
- 然后,我们使用两个辅助函数 findLeft 和 findRight 来分别查找目标值的开始位置和结束位置。
- 在 findLeft 函数中,我们使用二分查找来搜索目标值的开始位置。初始时,左边界 left 指向数组的第一个元素,右边界 right 指向数组的最后一个元素。在每次循环中,计算中间元素索引 mid,并将它与目标值进行比较。如果中间元素大于或等于目标值,则将右边界 right 缩小为 mid;否则,将左边界 left 扩大为 mid + 1。最后,返回 left 的值作为目标值的开始位置。如果目标值不存在,则返回 -1。
- 在 findRight 函数中,我们同样使用二分查找来搜索目标值的结束位置。不过这次的二分查找稍有不同。初始时,左边界 left 指向数组的第一个元素,右边界 right 指向数组的最后一个元素。在每次循环中,计算中间元素索引 mid,并将它与目标值进行比较。如果中间元素小于或等于目标值,则将左边界 left 扩大为 mid;否则,将右边界 right 缩小为 mid - 1。最后,返回 left 的值作为目标值的结束位置。如果目标值不存在,则返回 -1。
- 最后,在主函数 searchRange 中,我们首先判断特殊情况,即数组为空或长度为0的情况,直接返回初始化好的 result 数组。
- 然后,我们通过调用辅助函数 findLeft 和 findRight 分别得到目标值的开始位置和结束位置,并将它们存储在 result 数组中。
- 最后,返回 result 数组作为结果。
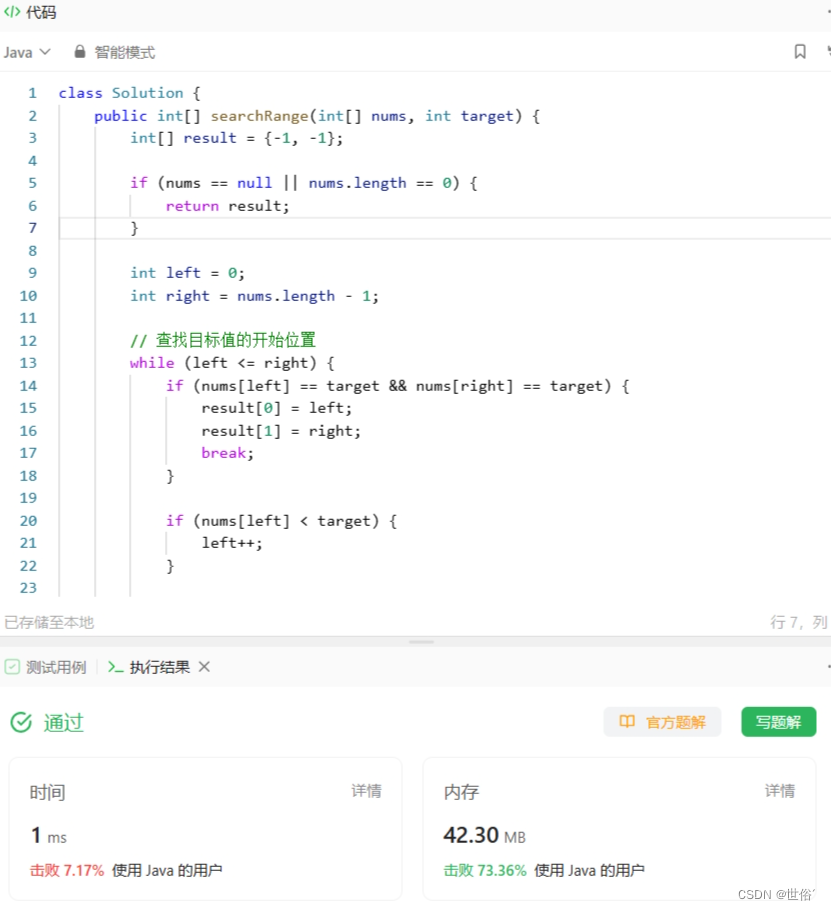
class Solution {public int[] searchRange(int[] nums, int target) {int[] result = {-1, -1};if (nums == null || nums.length == 0) {return result;}int leftIndex = findLeft(nums, target);int rightIndex = findRight(nums, target);if (leftIndex <= rightIndex) {result[0] = leftIndex;result[1] = rightIndex;}return result;}private int findLeft(int[] nums, int target) {int left = 0;int right = nums.length - 1;while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] >= target) {right = mid;} else {left = mid + 1;}}return nums[left] == target ? left : -1;}private int findRight(int[] nums, int target) {int left = 0;int right = nums.length - 1;while (left < right) {int mid = left + (right - left) / 2 + 1;if (nums[mid] <= target) {left = mid;} else {right = mid - 1;}}return nums[left] == target ? left : -1;}
}
复杂度分析:
- 时间复杂度:O(log n)。每次迭代都将搜索空间减半,因此时间复杂度为对数级别。
- 空间复杂度:O(1)。仅使用了有限的额外空间来存储几个变量。
LeetCode运行结果:

方法二:线性扫描
除了二分查找,还可以使用线性扫描的方法来搜索排序数组中目标值的开始位置和结束位置。
- 我们首先遍历整个数组来查找目标值的开始位置。如果找到目标值,我们将其索引存储在 result[0] 中并立即退出循环。如果没有找到目标值,则 result[0] 保持为初始值 -1。
- 接着,我们再从数组的末尾开始向前遍历,查找目标值的结束位置。如果找到目标值,我们将其索引存储在 result[1] 中并立即退出循环。如果没有找到目标值,则 result[1] 保持为初始值 -1。
- 最后,我们返回存储了目标值开始位置和结束位置的 result 数组。
class Solution {public int[] searchRange(int[] nums, int target) {int[] result = {-1, -1};if (nums == null || nums.length == 0) {return result;}for (int i = 0; i < nums.length; i++) {if (nums[i] == target) {result[0] = i;break;}}if (result[0] != -1) {for (int j = nums.length - 1; j >= 0; j--) {if (nums[j] == target) {result[1] = j;break;}}}return result;}
}
复杂度分析:
- 时间复杂度:O(n)。需要遍历整个数组,其中 n 是数组的长度。
- 空间复杂度:O(1)。仅使用了有限的额外空间来存储几个变量。
因为二分查找的时间复杂度为 log n,而线性扫描的时间复杂度为 n,所以在数组较大且已排序的情况下,二分查找的性能更好。它减少了搜索空间的大小,使得平均查找次数更低。然而,在数组较小或未排序的情况下,线性扫描是一种简单有效的方法。
LeetCode运行结果:

方法三:双指针
除了二分查找和线性扫描,还有一种常用的方法是双指针法。这种方法适用于有序数组或部分有序数组,并且可以在 O(n) 的时间复杂度内找到目标值的开始位置和结束位置。
class Solution {public int[] searchRange(int[] nums, int target) {int[] result = {-1, -1};if (nums == null || nums.length == 0) {return result;}int left = 0;int right = nums.length - 1;// 查找目标值的开始位置while (left <= right) {if (nums[left] == target && nums[right] == target) {result[0] = left;result[1] = right;break;}if (nums[left] < target) {left++;}if (nums[right] > target) {right--;}}return result;}
}
在上述代码中,我们使用两个指针 left 和 right 来标记搜索区间。通过不断更新指针的位置,我们可以确定目标值的开始位置和结束位置。
具体步骤如下:
- 初始化指针 left 和 right 分别指向数组的首尾元素。
- 当 left 指向的元素小于目标值时,将 left 向右移动一位。
- 当 right 指向的元素大于目标值时,将 right 向左移动一位。
- 如果 left 和 right 指向的元素都等于目标值,则找到了目标值的开始位置和结束位置。将结果存储在 result 数组中,并退出循环。
- 如果找不到目标值,则返回初始值为 -1 的 result 数组。
复杂度分析:
- 使用双指针法的时间复杂度是 O(n),其中 n 是数组的长度。在最坏的情况下,即目标值不在数组中或者目标值在数组中出现了 n 次,我们需要将指针 left 和 right 分别移动到数组的两端。因此,最多需要遍历整个数组一次,时间复杂度为 O(n)。
- 空间复杂度是 O(1),因为我们只需要使用有限的额外变量来记录指针的位置和存储结果数组。
需要注意的是,双指针法适用于有序数组或部分有序数组,如果数组无序,则双指针法无法正确找到目标值的开始位置和结束位置。
LeetCode运行结果:
相关文章:

怒刷LeetCode的第14天(Java版)
目录 第一题 题目来源 题目内容 解决方法 方法一:动态规划 方法二:栈 方法三:双指针 第二题 题目来源 题目内容 解决方法 方法一:二分查找 方法二:线性扫描 方法三:递归 第三题 题目来源 …...
c语言 static
1、静态局部变量在程序加载时初始化,静态局部变量的初始值写入到了data段: 如下代码test_symbol.c int f() {static int x 0;return x; }int g() {static int x 9;return x; }使用命令gcc -c test_symbol.c -o test_symbol 编译 使用命令 readelf -a …...

java基础3
输入一个班学生的成绩,先显示所有及格的成绩,再显示所有不及格的成绩,最后显示及格人数和不及格人数 import java.util.Scanner; public class Hello{public static void main(String [] args) {int SIZE5;double grade[] new double[SIZE]…...
LeetCode 1194.锦标赛优胜者
数据准备 Create table If Not Exists Players (player_id int, group_id int); Create table If Not Exists Matches (match_id int, first_player int, second_player int, first_score int, second_score int); Truncate table Players; insert into Players (player_id, g…...
多旋翼无人机组合导航系统-多源信息融合算法(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

如何用ArkUI实现一个加入购物车效果?
关键词:ArkUI的动效能力,动效开发,ArkUI动画 我们在购买商品时,往往习惯将商品先加入购物车,然后在购物车里确认后再下订单,这是一个典型的访问者模式。对于这个高频场景,增添一些动效可以增加a…...
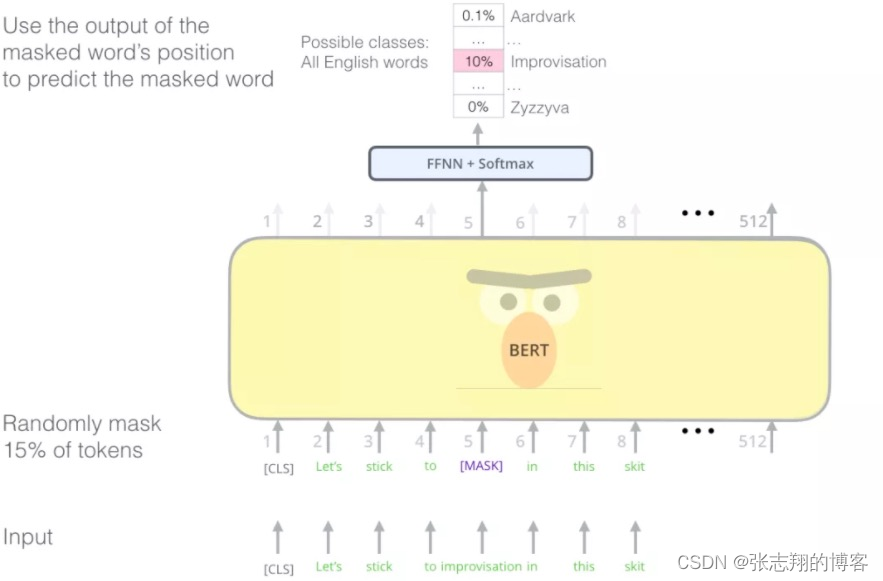
ChatGLM GPT原理介绍
图解GPT 除了BERT以外,另一个预训练模型GPT也给NLP领域带来了不少轰动,本节也对GPT做一个详细的讲解。 OpenAI提出的GPT-2模型(https://openai.com/blog/better-language-models/) 能够写出连贯并且高质量的文章,比之前语言模型效果好很多。GPT-2是基于Transformer搭建的,相…...
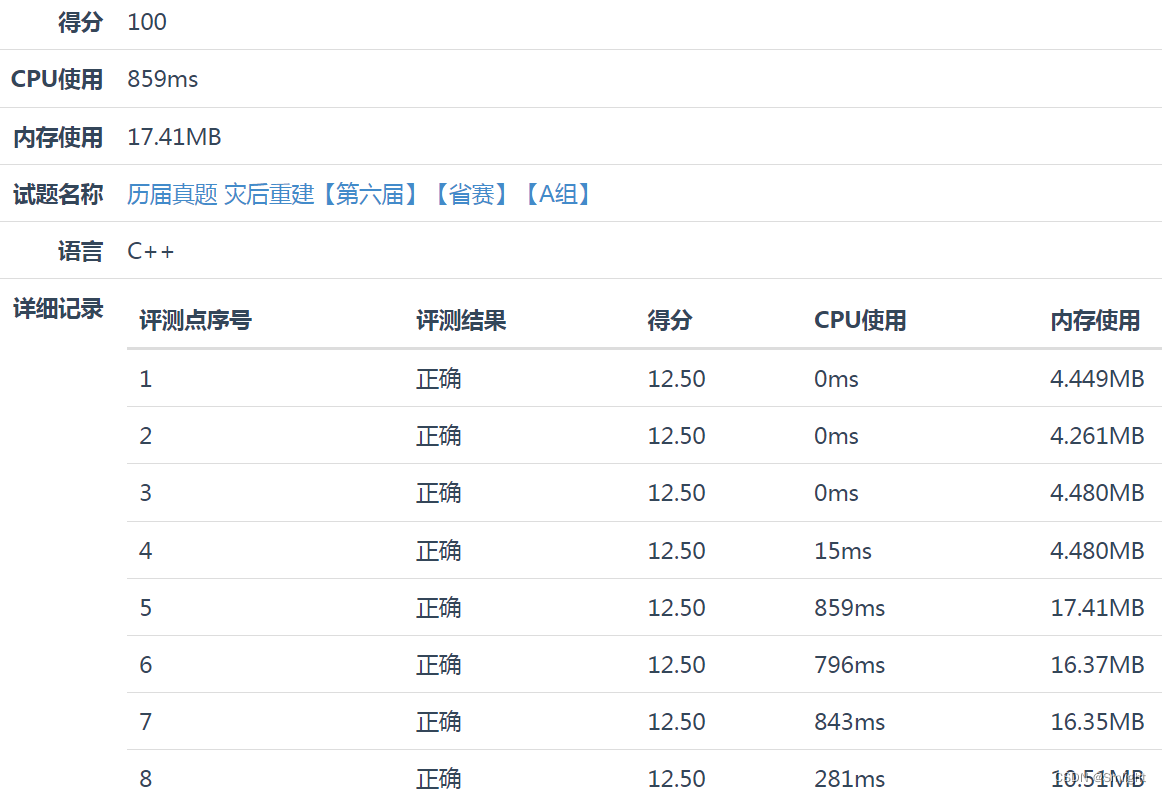
2015年蓝桥杯省赛C/C++ A组 灾后重建题解(100分)
10. 灾后重建 Pear市一共有N(<50000)个居民点,居民点之间有M(<200000)条双向道路相连。这些居民点两两之间都可以通过双向道路到达。这种情况一直持续到最近,一次严重的地震毁坏了全部M条道路。 震后…...
深分页Scroll)
Elasticsearch(四)深分页Scroll
一、前言 1.1、scroll与fromsize区别 ES对于fromsize的个数是有限制的,二者之和不能超过1w。当所请求的数据总量大于1w时,可用scroll来代替fromsize。 fromsize在ES查询数据的方式步骤如下: 1、先将用户指定的关键字进行分词;…...
JavaWeb后端开发 JWT令牌解析 登录校验 通用模板/SpringBoot整合
目录 实现思路 会话跟踪的三个方案--引出Jwt令牌技术 1.访问cookie的值,在同一会话的不同请求之间共享数据 2.session 3.现代普遍采用的令牌技术--JWT令牌 JWT令牌技术 第一步--生成令牌 1.引入依赖 2.生成令牌 第二步--校验令牌 第三步--登录下发令牌 需要解决的…...

Sparta工具用法描述之信息收集(漏洞分析)
声明:本文仅做学习与交流,任何用于非法用途、行为等造成他人损失的,责任自负。本文不承担任何法律责任。 Sparta是python GUI应用程序,它通过在扫描和枚举阶段协助渗透测试仪来简化网络基础结构渗透测试。 通过点击并单击工具箱并以方便的方式显示所有工具输出,它可以使测…...

Vue复选框批量删除示例
Vue复选框批量删除 通过使用v-model指令绑定单个复选框 例如<input type"checkbox" id"checkbox" v-model"checked"> 而本次我们要做的示例大致是这样的,首先可以增加内容,然后通过勾选来进行单独或者批量删除&…...

Docker自定义镜像
一、镜像结构 镜像是将应用程序及其需要的系统函数库、环境、配置、依赖打包而成。 镜像是分层结构,每一层称为一个Layer BaseImage层:包含基本的系统函数库、环境变量、文件系统其它:在BaseImage基础上添加依赖、安装程序、完成整个应用的…...

ardupilot的编译过程
环境 树莓派4b ubuntu20.04 git 2.25.1 python3.8.10 pixhawk2.4.8 下载源码 (已经配置好git环境和ssh) git clone --recurse-submodules gitgithub.com:ArduPilot/ardupilot.gitcd ardupilotgit status使用git status检查是否下载完整 如果不完整&a…...
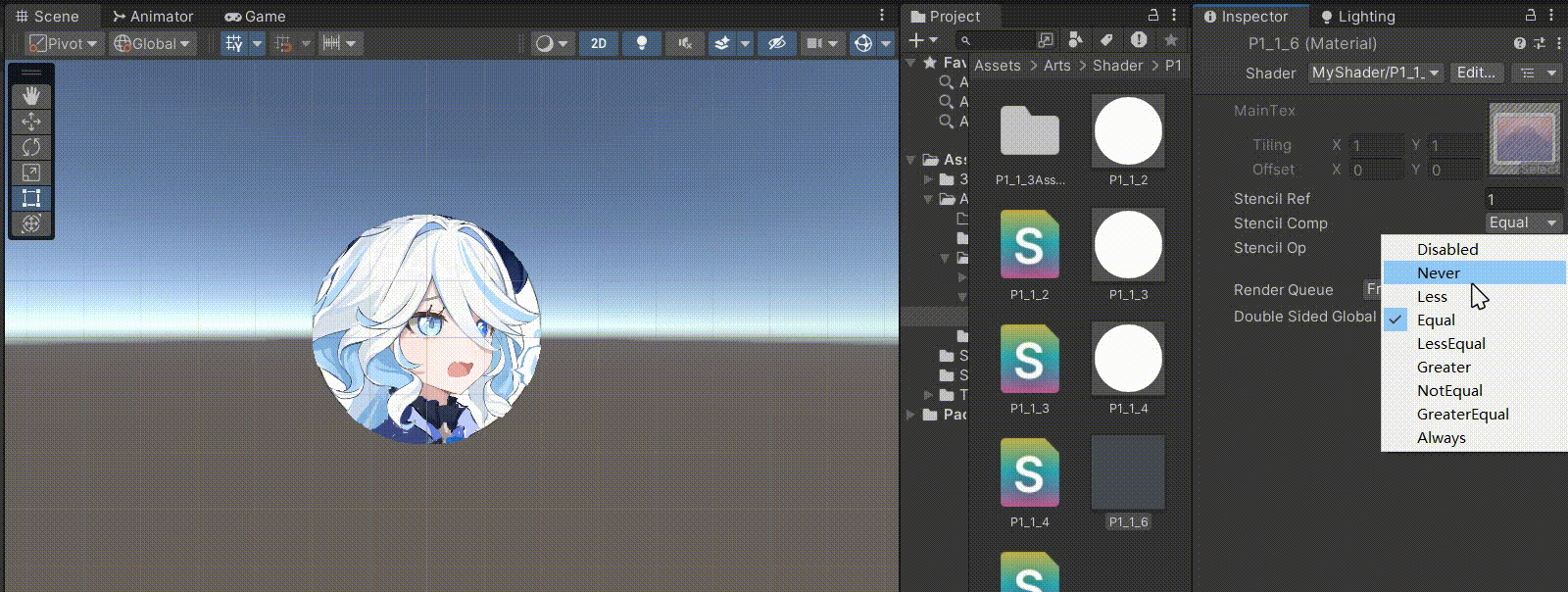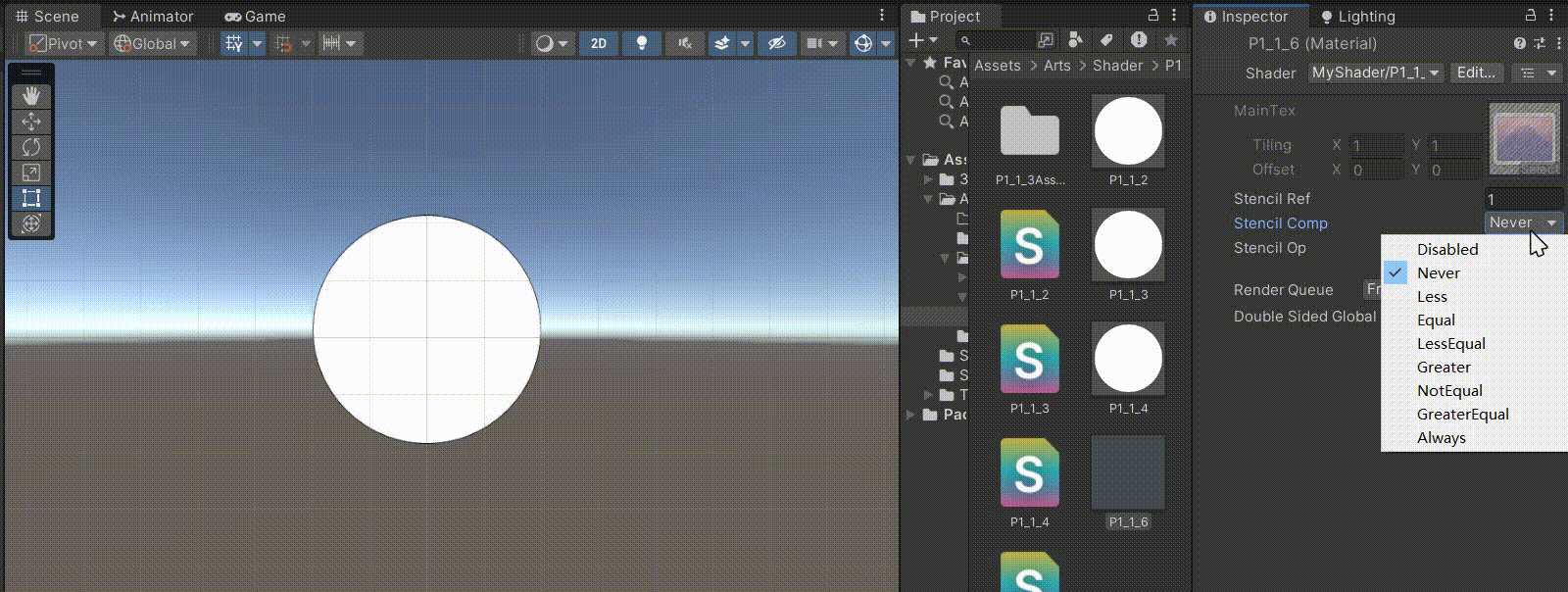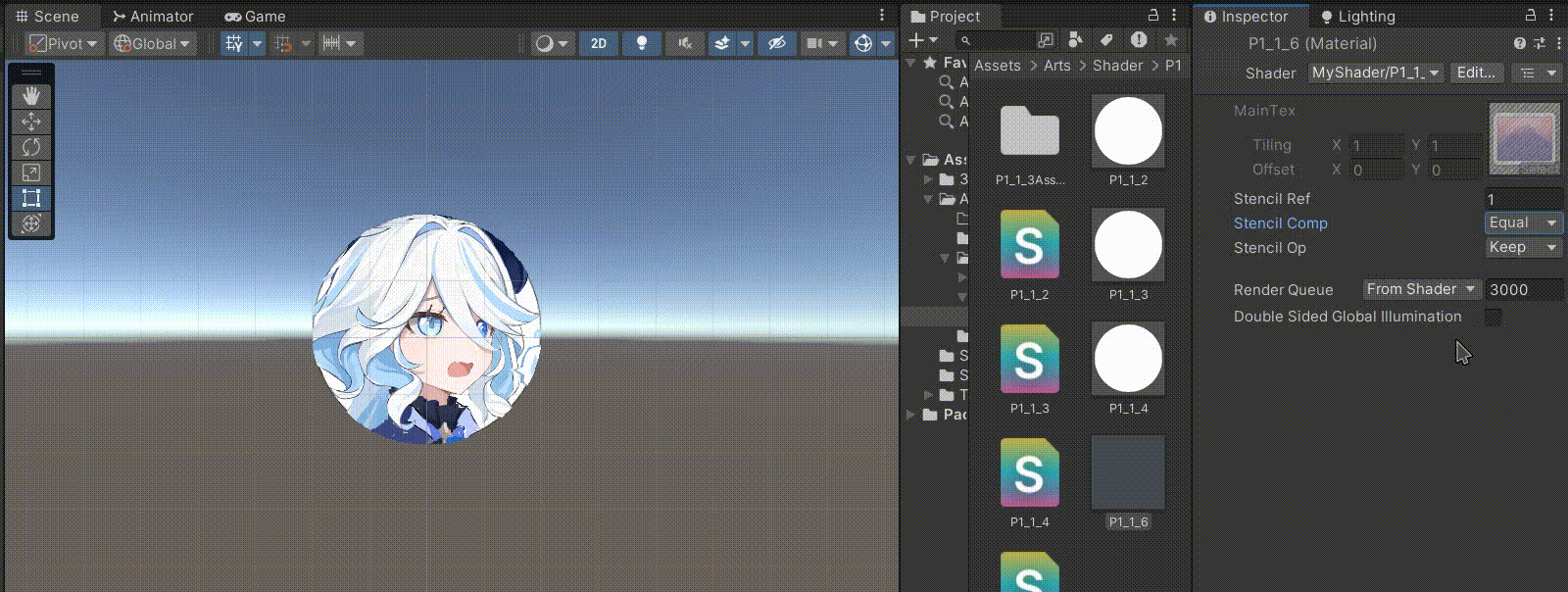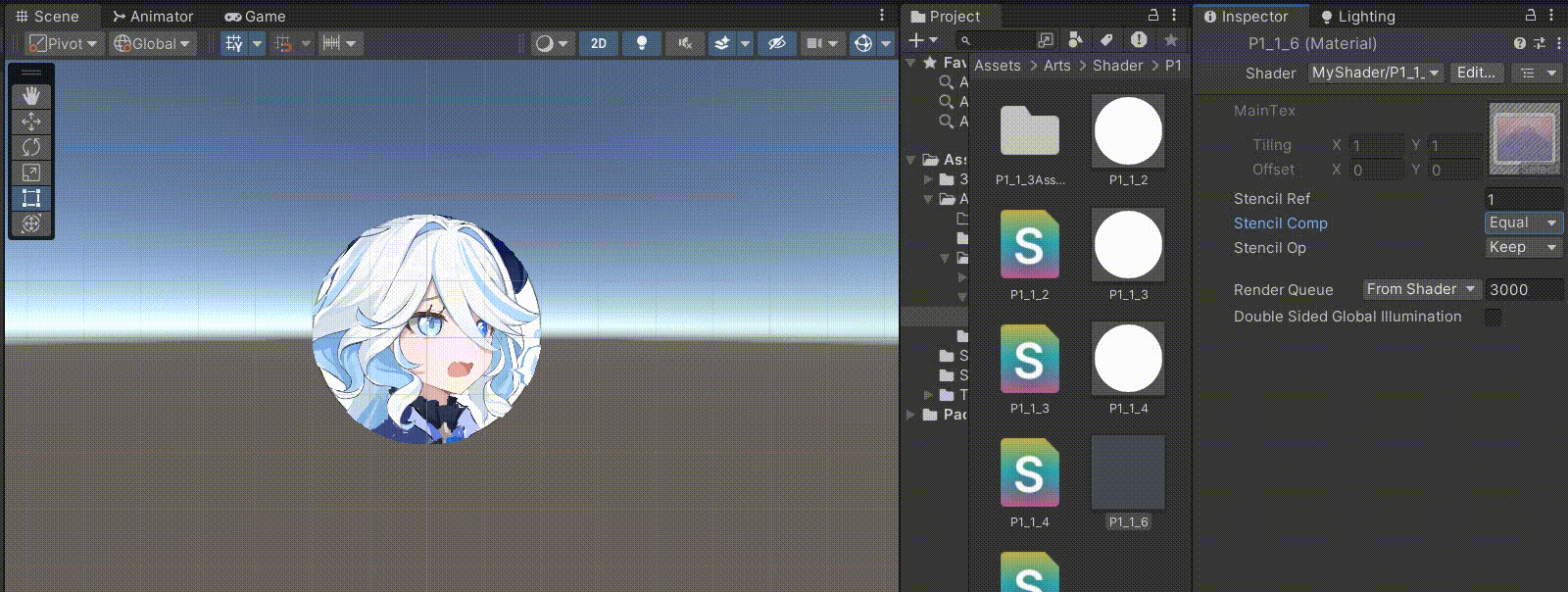
Unity中Shader实现模板测试Stencil
文章目录 前言一、UI中的遮罩1、Mask ——> 模板测试2、RectMask2D ——> UNITY_UI_CLIP_RECT 二、模板缓冲区Stencil一般是和Pass平行的部分,Pass部分写的是颜色缓冲区Stencil:Comp(比较操作)Pass(模版缓冲区的更新) 三、实际使用1、在…...

多线程与并发
多线程与高并发 线程的创建方式1.继承Thread类 重写run方法2.实现Runnable接口 重写run方法3. 实现Callable 重写call方法,配合FutureTask 线程的使用1.线程的状态1.1. 传统操作系统层面5种状态1.2.Java中给线程准备的6种状态 2.线程的常用方法2.1 获取当前线程2.2 …...

手写call方法
Function.prototype.myCallfunction (context,args) {console.log(arguments)//context 表示call里面的第一个参数也就是需要改变this指向的那个对象。//this表示这个方法//把这个方法挂到需要改变指向的对象身上调用,相当于把this指向了这个对象身上,从…...
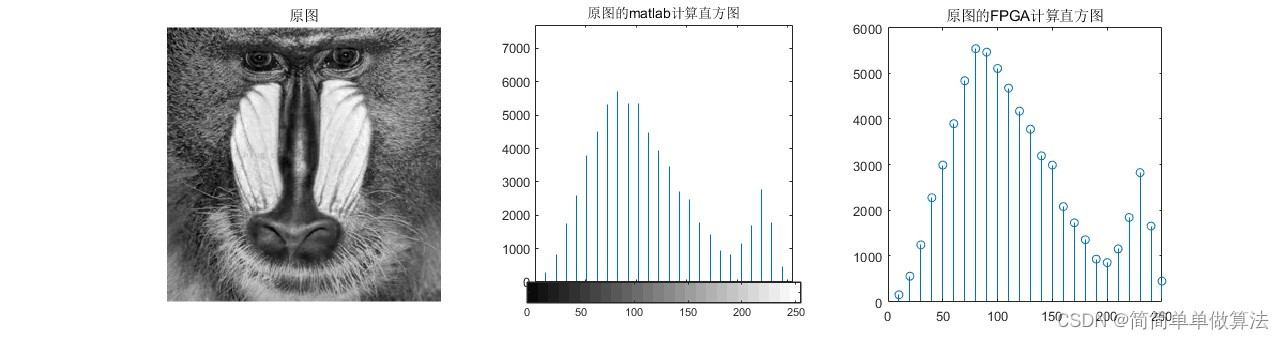
基于FPGA的图像直方图统计实现,包括tb测试文件和MATLAB辅助验证
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 4.1、图像数据传输 4.2、直方图统计算法 4.3、时序控制和电路设计 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 vivado2019.2 matlab2022a 3.部分核心程序 timescal…...
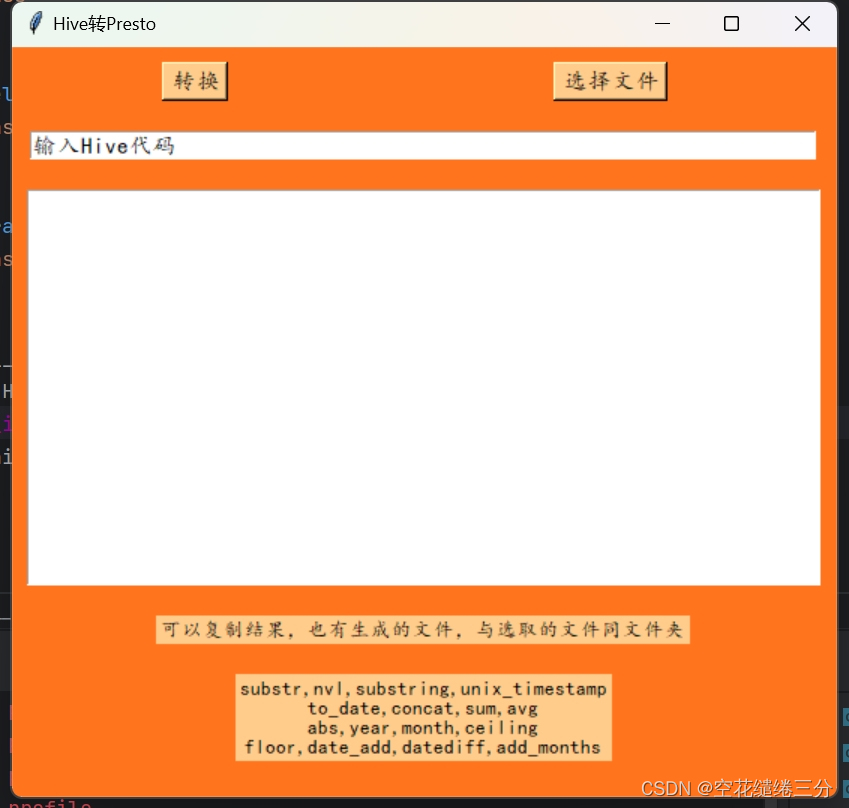
数据库:Hive转Presto(一)
本人因为工作原因,经常使用hive以及presto,一般是编写hive完成工作,服务器原因,presto会跑的更快一些,所以工作的时候会使用presto验证结果,所以就要频繁hive转presto,为了方便,我用…...

Responder
环境准备 操作系统:Kali Linux工具:responder,john,evil-winrm PS:输入以下命令解决靶场环境无法打开问题 #echo "<靶机IP> unika.htb">>/etc/hostsresponder工具 [Kali 官网] 手册地址:https://www.kali.org/tools/responder/ 摘要: This package c…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

深度解析云存储:概念、架构与应用实践
在数据爆炸式增长的时代,传统本地存储因容量限制、管理复杂等问题,已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性,成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理,云存储正重塑数据存储与…...
