34.CSS魔线图标的悬停效果
效果
源码
index.html
<!DOCTYPE html>
<html>
<head>
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<title>Icon Fill Hover Effects</title>
<link rel="stylesheet" href="https://stackpath.bootstrapcdn.com/font-awesome/4.7.0/css/font-awesome.min.css" integrity="sha384-wvfXpqpZZVQGK6TAh5PVlGOfQNHSoD2xbE+QkPxCAFlNEevoEH3Sl0sibVcOQVnN" crossorigin="anonymous">
<link rel="stylesheet" type="text/css" href="style.css">
</head>
<body><ul><li style="--clr:#1da1f2"><i class="fa fa-twitter"></i></li><li style="--clr:#dd2a7b"相关文章：
34.CSS魔线图标的悬停效果
效果 源码 index.html <!DOCTYPE html> <html> <head> <meta name="viewport" content="width=device-width, initial-scale=1.0"> <title>Icon Fill Hover Effects</title> <link rel="stylesheet" h…...
Django — 会话
目录 一、Cookie1、介绍2、作用3、工作原理4、结构5、用途6、设置7、获取 二、Session1、介绍2、作用3、工作原理3、类型4、用途5、设置6、获取7、清空信息 三、Cookie 和 Session 的区别1、存储位置2、安全性3、数据大小4、跨页面共享5、生命周期6、实现机制7、适用场景 四、P…...
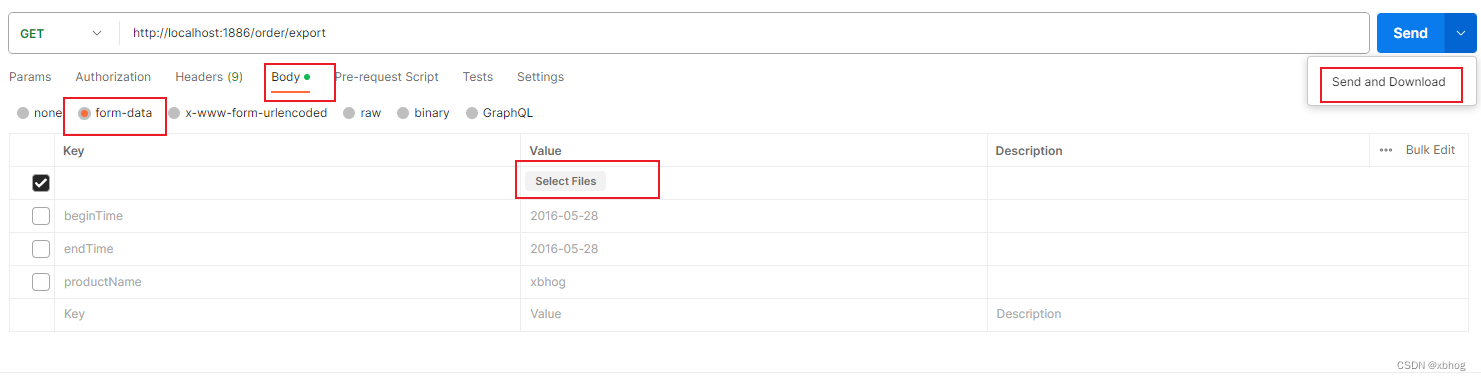
SpringBoot集成easypoi实现execl导出
<!--easypoi依赖，excel导入导出--><dependency><groupId>cn.afterturn</groupId><artifactId>easypoi-spring-boot-starter</artifactId><version>4.4.0</version></dependency>通过Exce注解设置标头名字和单…...
第9章 【MySQL】InnoDB的表空间
表空间 是一个抽象的概念，对于系统表空间来说，对应着文件系统中一个或多个实际文件；对于每个独立表空间来说，对应着文件系统中一个名为 表名.ibd 的实际文件。大家可以把表空间想象成被切分为许许多多个 页 的池子，当我…...
工作、生活常用免费api接口大全
手机号码归属地：提供三大运营商的手机号码归属地查询。全国快递物流查询：1.提供包括申通、顺丰、圆通、韵达、中通、汇通等600快递公司在内的快递物流单号查询。2.与官网实时同步更新。3.自动识别快递公司。IP归属地-IPv4区县级：根据IP地址查…...
寻找单身狗
在一个数组中仅出现一次，其他数均出现两次，这个出现一次的数就被称为“单身狗“。 一.一个单身狗 我们知道异或运算操作符 ^ ，它的特点是对应二进制位相同为 0，相异为 1。 由此我们容易知道两个相同的数,进行异或运算得到的结果…...
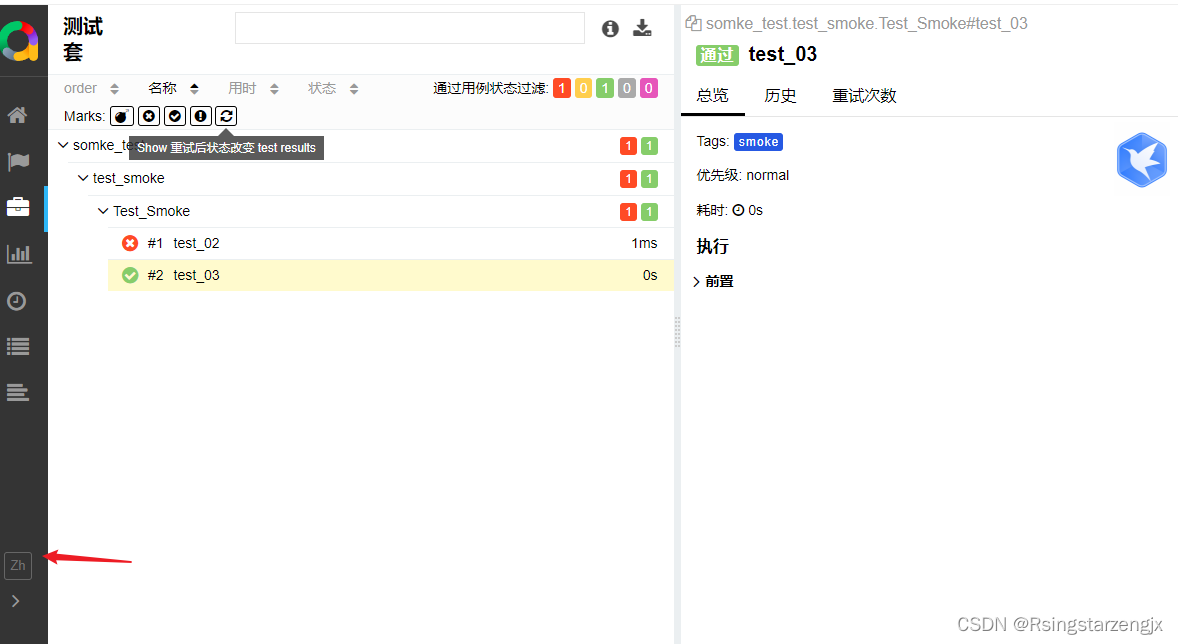
【pytest】 allure 生成报告
1. 下载地址 官方文档; Allure Framework 参考文档： 最全的PytestAllure使用教程，建议收藏 - 知乎 https://github.com/allure-framework 1.2安装Python依赖 windows：pip install allure-pytest 2. 脚本 用例 import pytest class …...
动态链接库搜索顺序
动态链接库搜索顺序 同一动态链接库 (DLL) 的多个版本通常存在于操作系统 (OS) 内的不同文件系统位置。 可以通过指定完整路径来控制从中加载任何给定 DLL 的特定位置。 但是，如果不使用该方法，则系统会在加载时搜索 DLL，如本主题中所述。 DL…...
【CAN、LIN通信的区分】
CAN和LIN是两种不同的通信协议，用于不同的应用场景。CAN（Controller Area Network）是一种高速、可靠、多节点的串行通信协议，主要用于汽车电子领域的高速数据传输和控制；而LIN（Local Interconnect Network&…...
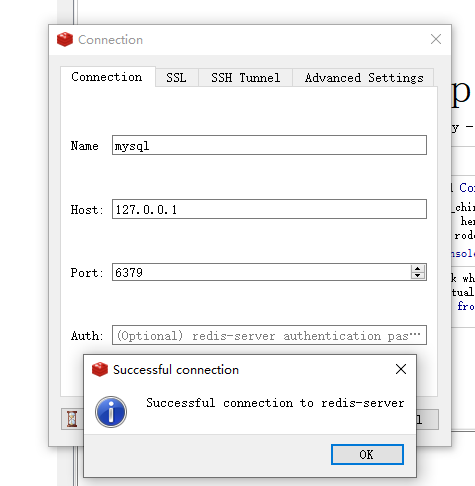
Redis环境配置
【Redis解压即可】链接：https://pan.baidu.com/s/1y4xVLF8-8PI8qrczbxde9w?pwd0122 提取码：0122 【Redis桌面工具】 链接：https://pan.baidu.com/s/1IlsUy9sMfh95dQPeeM_1Qg?pwd0122 提取码：0122 Redis安装步骤 1.先打开Redis…...
-采用std::vector对体对象的质心进行排序)
UG NX二次开发(C++)-采用std::vector对体对象的质心进行排序
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录 1、前言2、体对象质心结构体的构造3、采用NXOpen获取part中的所有体对象4、通过遍历体对象集合来实现std::vector<MyBody>的赋值5、对结构体排序6、调用的完整源代码7、生成dll并测试一、pan…...
一点思考｜关于「引领性研究」的一点感悟
前言：调研过这么多方向之后，对研究方向的产生与发展具备了一些自己的感悟，尤其是在AI安全领域。私认为，所谓有价值、有意义的研究，就是指在现实社会中能够产生波澜、为国家和社会产生一定效益的研究。 举例来说&#x…...
什么是HTTP/2？它与HTTP/1.1相比有什么改进？
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ HTTP/2 简介⭐ 主要的改进和特点⭐ 总结⭐ 写在最后 ⭐ 专栏简介 前端入门之旅：探索Web开发的奇妙世界 欢迎来到前端入门之旅！感兴趣的可以订阅本专栏哦！这个专栏是为那些对Web开发感兴趣、刚刚踏入前端…...
IDEA
快捷键 好用的快捷键，可以使写代码变得更加便捷~ IntelliJ IDEA具有许多有用的快捷键，这些快捷键可以帮助开发人员更快速、高效地编写和管理代码。以下是一些常用的IntelliJ IDEA快捷键，这些快捷键在Java开发中特别有用： 基本编辑…...
NSS [HXPCTF 2021]includer‘s revenge
NSS [HXPCTF 2021]includer’s revenge 题目描述：Just sitting here and waiting for PHP 8.1 (lolphp). 题目源码：（index.php） <?php ($_GET[action] ?? read ) read ? readfile($_GET[file] ?? index.php) : inclu…...
《动手学深度学习 Pytorch版》 7.1 深度卷积神经网络(AlexNet)
7.1.1 学习表征 深度卷积神经网络的突破出现在2012年。突破可归因于以下两个关键因素： 缺少的成分：数据 数据集紧缺的情况在 2010 年前后兴起的大数据浪潮中得到改善。ImageNet 挑战赛中，ImageNet数据集由斯坦福大学教授李飞飞小组的研究人…...
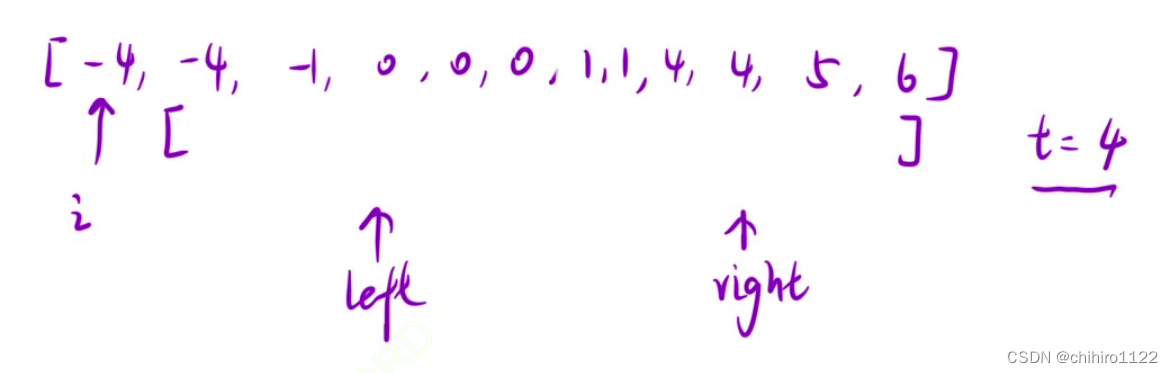
C++ - 双指针_盛水最多的容器
盛水最多的容器 11. 盛最多水的容器 - 力扣（LeetCode） 给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的…...
分类预测 | Matlab实现NGO-CNN-SVM北方苍鹰算法优化卷积支持向量机分类预测
分类预测 | Matlab实现NGO-CNN-SVM北方苍鹰算法优化卷积支持向量机分类预测 目录 分类预测 | Matlab实现NGO-CNN-SVM北方苍鹰算法优化卷积支持向量机分类预测分类效果基本描述程序设计参考资料 分类效果 基本描述 1.Matlab实现NGO-CNN-SVM北方苍鹰算法优化卷积支持向量机分类预…...
分享一个java+springboot+vue校园电动车租赁系统（源码、调试、开题、lw）
💕💕作者：计算机源码社 💕💕个人简介：本人七年开发经验，擅长Java、Python、PHP、.NET、微信小程序、爬虫、大数据等，大家有这一块的问题可以一起交流！ 💕&…...
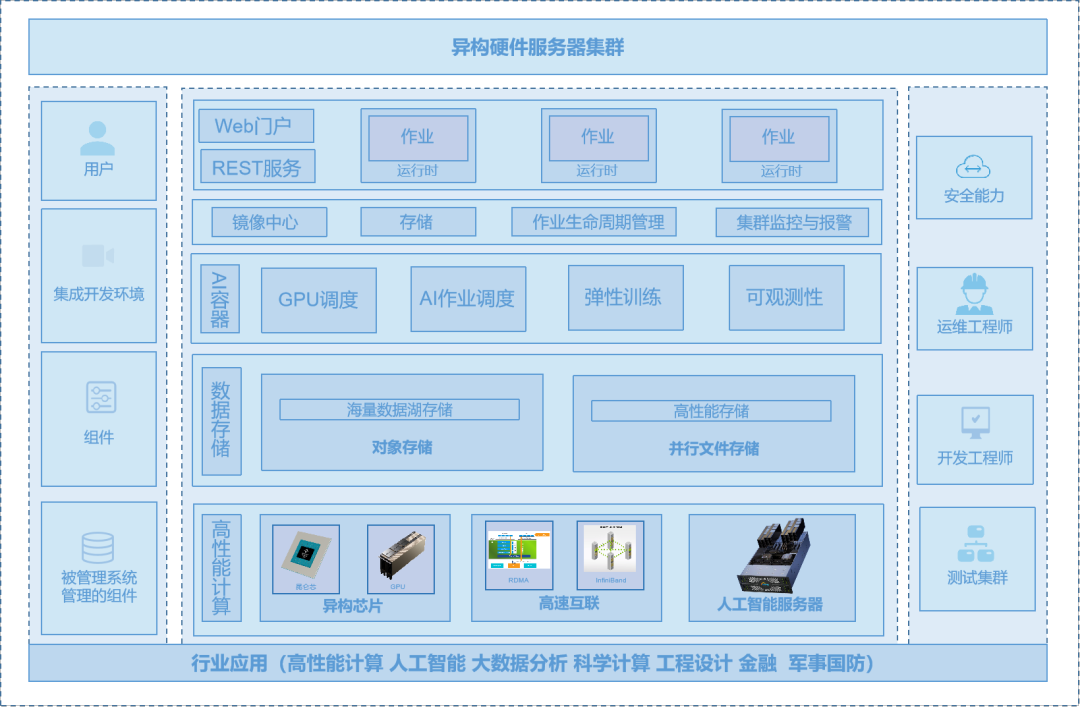
高性能计算环境下的深度学习异构集群建设与优化实践
★深度学习；模式识别；图像处理；人工智能建模；人工智能；深度学习算法；强化学习；神经网络；卷积神经网络；人工神经网络；VIBE算法；控制系统仿真&#…...
观成科技：隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具，该工具基于TUN接口实现其功能，利用反向TCP/TLS连接建立一条隐蔽的通信信道，支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式，适应复杂网…...
谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0：开发环境同步测试 cookie 至 localhost，便于本地请求服务携带 cookie 参考地址：https://juejin.cn/post/7139354571712757767 里面有源码下载下来，加在到扩展即可使用FeHelp…...
使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架，专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用，其中包含三个使用通用基本模板的页面。在此…...
Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题： 下面创建一个简单的Flask RESTful API示例。首先，我们需要创建环境，安装必要的依赖，然后…...
CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框，很难让人不联想到SQL注入，但提示都说了不是SQL注入，所以就不往这方面想了 先查看一下网页源码，发现一段JavaScript代码，有一个关键类ctfs…...
树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源： http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作，无需更改相机配置。但是，一…...
React Native 导航系统实战（React Navigation）
导航系统实战（React Navigation） React Navigation 是 React Native 应用中最常用的导航库之一，它提供了多种导航模式，如堆栈导航（Stack Navigator）、标签导航（Tab Navigator）和抽屉…...
大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动（如演唱会、马拉松赛事、高考中考等）期间，城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例，暖城商圈曾因观众集中离场导致周边…...
srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935，SRS管理页面端口是8080，可…...
linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行，YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID： YW3…...