论文速览【序列模型 seq2seq】—— 【Ptr-Net】Pointer Networks
- 标题:Pointer Networks
- 文章链接:Pointer Networks
- 参考代码(非官方):keon/pointer-networks
- 发表:NIPS 2015
- 领域:序列模型(RNN seq2seq)改进 / 深度学习解决组合优化问题
- 【本文为速览笔记,仅记录核心思想,具体细节请看原文】
- 摘要:我们引入了一种新的神经网络结构,用于学习一个输出序列的条件概率,其中输出序列的元素是对应于输入序列位置的离散标记。这类问题不能通过Seq2Seq模型和神经图灵机等现有方法轻松解决,因为(这些问题中)输出每一步的目标类别数量取决于输入的长度,而输入的长度是可变的。排序可变长度序列、各种组合优化问题等属于这类问题。我们的模型使用了最近提出的神经注意力机制,来解决可变长度输出字典的问题。与先前的注意力机制不同的是,我们的模型不是在每个解码器步骤中将编码器的隐藏单元与上下文向量混合,而是使用注意力作为指针来选择输入序列的成员作为输出。我们将这种结构称为指针网络(Ptr-Net)。我们在平面凸包(planar convex hulls)、计算德劳内三角剖分(computing Delaunay triangulations)和旅行商问题(TSP)三个有挑战性的几何问题上验证了指针网络有能力以 Data-driven 的形式学到近似解。指针网络不仅改进了具有输入注意力的序列到序列模型,还能够推广到可变长度输出字典。我们展示了训练的模型在超过其训练最大长度的情况下也能泛化
文章目录
- 0. 本文考虑的问题
- 1. 传统方法及其问题
- 1.1 Sequence-to-Sequence Model
- 1.2 Content Based Input Attention
- 1.3 问题
- 2. 本文方法
- 3. 实验
- 4. 总结
0. 本文考虑的问题
-
本文主要考虑那些 “输出序列是离散的,并对应于输入序列中位置” 的 Seq2Seq 问题。实验的问题包括
平面凸包问题planar convex hulls:给定平面上若干个点的坐标,输出一组点的索引,使得这些点围成的多边形可以覆盖所有点计算德劳内三角剖分computing Delaunay triangulations:给定平面上若干个点的坐标,以点索引形式输出德劳内三角剖分结果(这是一种以最近的三点形成三角形,且各线段皆不相交的三角网剖分方式)
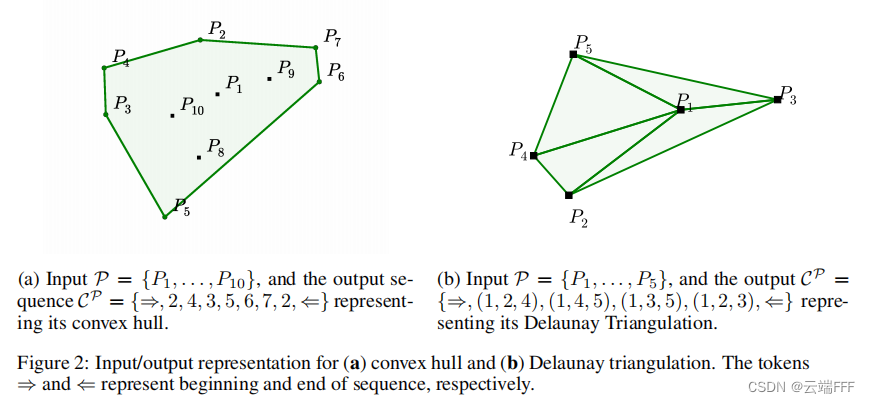
除了以上两个例子外,很多组合优化问题也具有这种形式,作者测试了 Tsp 问题。作者开源了以上三类问题的数据集
-
注意这类问题的特点是:
输出序列的每个元素都是输入序列包含的位置索引,输入序列长度 = 输出索引范围
1. 传统方法及其问题
1.1 Sequence-to-Sequence Model
- 本文是对 Seq2Seq 模型的一个改进,Seq2Seq 模型用于把一个序列转换成另外一个序列,且不要求输入序列和输出序列等长,典型应用有机器翻译等

如上图所示,Seq2Seq 模型通常使用 RNN 及其变种(LSTM/GRU)以 encoder-decoder 结构构建。RNN 类模型内部有一个隐状态代表目前积累的信息,每读入一个序列样本就将其更新,隐变量值可以较好地捕获前驱序列特征。通常使用两个独立的 RNN 模型,一个作为 encoder 提取输入序列的特征,另一个作为 decoder 以 Autoregress 形式解码得到输出序列 - 考虑第 0 节的问题,形式化地讲,给定训练样例 ( P , C P ) (\mathcal{P}, \mathcal{C^P}) (P,CP),Seq2Seq 模型使用参数模型计算条件概率
p ( C P ∣ P ; θ ) = p ( C 2 ∣ C 1 , P ; θ ) ⋅ p ( C 3 ∣ C 2 , C 1 , P ; θ ) ⋅ ⋅ ⋅ p ( C m ( P ) ∣ C m ( P ) − 1 , C m ( P ) − 2 , . . . , C 0 , P ; θ ) = ∏ i = 1 m ( P ) p ( C i ∣ C 1 , … , C i − 1 , P ; θ ) \begin{aligned} p(\mathcal{C}^{\mathcal{P}}|\mathcal{P};\theta) &= p (C_2|C_1,\mathcal{P};\theta)·p (C_3|C_2,C_1,\mathcal{P};\theta) ···p (C_{m(\mathcal{P})}|C_{m(\mathcal{P})-1},C_{m(\mathcal{P})-2},...,C_0,\mathcal{P};\theta) \\ &=\prod_{i=1}^{m(\mathcal{P})}p (C_{i}|C_{1},\ldots,C_{i-1},\mathcal{P};\theta) \end{aligned} p(CP∣P;θ)=p(C2∣C1,P;θ)⋅p(C3∣C2,C1,P;θ)⋅⋅⋅p(Cm(P)∣Cm(P)−1,Cm(P)−2,...,C0,P;θ)=i=1∏m(P)p(Ci∣C1,…,Ci−1,P;θ) 其中 P = { P 1 , … , P n } \mathcal{P}=\{P_{1},\ldots,P_{n}\} P={P1,…,Pn} 是包含 n n n 个向量的输入序列(上图中的 v v v), C P = { C 1 , … , C m ( P ) } \mathcal{C}^{\mathcal{P}}=\{C_{1},\ldots,C_{m(\mathcal{P})}\} CP={C1,…,Cm(P)} 是由 m ( P ) m(\mathcal{P}) m(P) 个索引组成的序列,每个索引取值范围为 [ 1 , n ] [1,n] [1,n]。直观地看这个条件概率就是模型解码出目标序列的概率。注意目标序列的长度 m ( P ) m(\mathcal{P}) m(P) 通常取决于 P \mathcal{P} P。学习目标是最大化训练集中所有样本的上述概率之和,即
θ ∗ = arg max θ ∑ P , C P log p ( C P ∣ P ; θ ) , \theta^{*}=\operatorname*{arg\,max}_{\theta}\sum_{\mathcal{P},\mathcal{C}^{ \mathcal{P}}}\log p(\mathcal{C}^{\mathcal{P}}|\mathcal{P};\theta), θ∗=θargmaxP,CP∑logp(CP∣P;θ), 训练之后评估阶段,给定输入序列 P \mathcal{P} P,使用学习到的参数 θ ∗ \theta^{*} θ∗ 选择具有最高概率的序列
C ^ P = arg max C P p ( C P ∣ P ; θ ∗ ) \hat{\mathcal{C}}^{\mathcal{P}}=\operatorname*{arg\,max}_{\mathcal{C}^{\mathcal{P}}}p(\mathcal{C}^{\mathcal{P}}|\mathcal{P};\theta^{*}) C^P=CPargmaxp(CP∣P;θ∗) 由于输出序列空间大小为 n m ( P ) n^{m(\mathcal{P})} nm(P),找到真正的最大概率输出序列的计算量太大,工程上通常使用贪心或者 beam search 方法进行解码
1.2 Content Based Input Attention
-
RNN 类模型只能利用隐状态间接地获取之前序列的信息,由于隐藏状态维度一定远远小于之前的变长序列所有样本的连接维度,这种做法无可避免地会损失一些信息。一种补偿方式是引入额外的 Attention 模块,它对整个输入序列的所有 hidden state e 1 , . . . , e n e_1,...,e_n e1,...,en 构造 key 向量,之后在任意第 i i i 个解码位置,用其 hidden state d i d_i di 构造 query 并和整个输入序列计算 attention,根据 attention 结果汇聚(加权平均)整个输入序列的 hidden state,最后用得到的结果和 d i d_i di 做 concatenate 来增强解码时信息输入,缓解信息损耗问题。下图是一个示意

-
形式化地,设 encoder 和 decoder 的隐藏状态为 ( e 1 , … , e n ) (e_{1},\ldots,e_{n}) (e1,…,en) 和 ( d 1 , … , d m ( P ) ) (d_{1},\ldots,d_{m(\mathcal{P})}) (d1,…,dm(P)),如下计算每个输出时刻 i i i 的附加信息
u j i = v T tanh ( W 1 e j + W 2 d i ) j ∈ ( 1 , … , n ) a j i = softmax ( u j i ) j ∈ ( 1 , … , n ) d i ′ = ∑ j = 1 n a j i e j \begin{aligned} u_{j}^{i} & =v^{T} \tanh \left(W_{1} e_{j}+W_{2} d_{i}\right) & j \in(1, \ldots, n) \\ a_{j}^{i} & =\operatorname{softmax}\left(u_{j}^{i}\right) & j \in(1, \ldots, n) \\ d_{i}^{\prime} & =\sum_{j=1}^{n} a_{j}^{i} e_{j} & \end{aligned} ujiajidi′=vTtanh(W1ej+W2di)=softmax(uji)=j=1∑najiejj∈(1,…,n)j∈(1,…,n) 注意这里使用了比较早期的加性注意力,向量 v v v 和矩阵 W 1 , W 2 W_1,W_2 W1,W2 是三组要学习的参数。最后用增强后的 [ d i , d i ′ ] [d_i, d_i'] [di,di′] 作为隐状态进行解码。这种方式相对 1.1 节的朴素 Seq2Seq 方法有显著性能提高
1.3 问题
- 以上两个方法虽然也能部分解决第 0 节的问题,但它们都有一个显著缺陷,即处理问题的尺度无法随着输入泛化:对于每个不同的输入长度 n n n 都要单独训练一个模型。这个问题的本质在于模型无法动态地从输入序列中构造词表,训练时都是事先根据问题规模设置好词表大小的
2. 本文方法
- 作者解决 1.3 节问题的思路很直接,他注意随着输入序列长度的变化,attention 范围可以自适应地变化,所以解码过程中只要想办法自回归地让 attention 像指针一样指出输入序列中的目标位置即可。这其实是对 1.2 节 decoder 的一种简化,我们不再需要根据 attention 汇聚特征再做分类任务,而是直接用经过 softmax 的 attention 向量做分类,这样输出空间可以根据输入序列长度自动调整。示意图如下

图(a) 是 1.1 节的朴素 Seq2Seq 模型,图(b) 是作者提出的指针网络模型 - 形式化地,如下用 attention 机制改写 1.1 节中对 p ( C i ∣ C 1 , … , C i − 1 , P ) p(C_{i}|C_{1},\ldots,C_{i-1},\mathcal{P}) p(Ci∣C1,…,Ci−1,P) 建模的方式
u j i = v T tanh ( W 1 e j + W 2 d i ) j ∈ ( 1 , … , n ) p ( C i ∣ C 1 , … , C i − 1 , P ) = softmax ( u i ) \begin{aligned} u_{j}^{i} & =v^{T} \tanh \left(W_{1} e_{j}+W_{2} d_{i}\right) \quad j \in(1, \ldots, n) \\ p\left(C_{i} \mid C_{1}, \ldots, C_{i-1}, \mathcal{P}\right) & =\operatorname{softmax}\left(u^{i}\right) \end{aligned} ujip(Ci∣C1,…,Ci−1,P)=vTtanh(W1ej+W2di)j∈(1,…,n)=softmax(ui) 这里 u j i u_j^i uji 是长度为 n n n 的注意力得分向量, softmax \operatorname{softmax} softmax 操作将其转换为输入序列上的分布,直接把这个 attention 分布看作在尺寸为 n n n 的词表上做分类时的 softmax 分布,使用交叉熵损失进行优化即可
3. 实验
- 这里仅介绍 TSP 上的结果,另外两个问题详见论文
TSP 问题是说给定一个城市列表,希望找到一个最短的路线,要求把每个城市访问一次并能返回到起点。作者假设两个城市之间的距离是对称的,即 A->B 的距离 = B-> A 的距离。
- 数据生成: 任意训练样本 ( P , C P ) (\mathcal{P}, \mathcal{C^P}) (P,CP) 中, P = { P 1 , … , P n } \mathcal{P}=\{P_{1},\ldots,P_{n}\} P={P1,…,Pn} 是在 [0,1]×[0,1] 区间中随机采样的 n n n 个笛卡尔坐标, C P = { C 1 , . . . , C n } \mathcal{C^P} = \{C_1,...,C_n\} CP={C1,...,Cn} 是一个从 1 到 n 的排列,代表最优路线。为了一致性,在训练数据集中,数据集总是从第一个城市开始。为了生成精确的数据,城市数量不一样,所构建的数据集输出结果方式也不一样,具体地说: 在城市数量 n ≤ 20 n\leq 20 n≤20 的情况下,采用 Held-Karp 算法;对于 n > 20 n>20 n>20 的情况,作者考虑了 A1 A2 A3 三种启发式搜索算法,其中 A3 算法保证在离最优长度1.5倍的范围内找到一个解
- 模型设置:所有模型都使用了具有 256 或 512 个隐藏单元的单层 LSTM;使用随机梯度下降(SGD)训练;学习率为1.0;batch_size为128;随机均匀权重初始化从 -0.08 到 0.08;L2正则化梯度裁剪为 2.0
- 实验结果如下

- 由于 TSP 问题是有约束的(不能重复访问城市,也不能忽略城市),作者在解码时的波束搜索(beam Search)过程中过滤有效的结果。这种过滤过程在 n > 20 n>20 n>20 时是必须的。当 n = 30 n=30 n=30 时(超过训练时城市数量),失败率到达 30%;当 n = 40 n=40 n=40 时失败率上升到 98%
- 表中 OPTIMAL 列是真实最优结果,缺少 n = 50 n=50 n=50 的结果是因为计算复杂度太高了
- 表中第一组行显示了在 n n n 相同时使用最优数据训练的结果。注意到使用最差的算法 (A1) 数据来训练 Ptr-Net 时,模型优于其试图模仿的A1算法(6.42 < 6.46)
- 表中第二组行显示了在5~20个城市的最佳数据上训练的 Ptr-Nets 如何能够推广到更多的城市。 结果对于n=25来说几乎是完美的,对于n=30来说是好的,但在40或更长的时间里似乎会崩溃(尽管如此,结果还是比随机策略要好得多)
4. 总结
- Pointer Networks 天生具备从输入序列中提取元素的能力,因此它非常适合用来实现 “复制” 这个功能。NLP 领域很多研究者也确实把它用于复制源文本中的一些词汇。比如摘要任务,由于所需的词汇较多,非常适合使用复制的方法来复制一些词,目前Pointer Networks 已经称为了文本摘要方法中的利器。
- 此外,在组合优化领域,Ptr-Nets 也得到了广泛的应用,并已成为组合优化问题的端到端方法的入门模型,后来基于此模型,研究者也进行了很多改进,比如与强化学习结合,将 Attention 换成 Transformer 中采用的Self- Attention等。总之,Ptr-Nets为组合优化的端到端解决办法起了一个好头,并促使广大研究者进行更加深入的研究
相关文章:

论文速览【序列模型 seq2seq】—— 【Ptr-Net】Pointer Networks
标题:Pointer Networks文章链接:Pointer Networks参考代码(非官方):keon/pointer-networks发表:NIPS 2015领域:序列模型(RNN seq2seq)改进 / 深度学习解决组合优化问题【…...
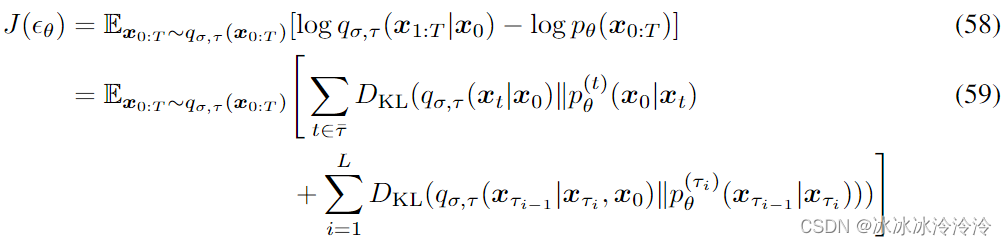
Denoising diffusion implicit models 阅读笔记
Denoising diffusion probabilistic models (DDPMs)从马尔科夫链中采样生成样本,需要迭代多次,速度较慢。Denoising diffusion implicit models (DDIMs)的提出是为了加速采样过程,减少迭代的次数,并且要求DDIM可以复用DDPM训练的网…...

【Java 基础篇】Executors工厂类详解
在多线程编程中,线程池是一项重要的工具,它可以有效地管理和控制线程的生命周期,提高程序的性能和可维护性。Java提供了java.util.concurrent包来支持线程池的创建和管理,而Executors工厂类是其中的一部分,它提供了一些…...

SpringBoot MongoDB操作封装
1.引入Jar包 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-mongodb</artifactId></dependency> 2.MongoDbHelper操作 /*** MongoDB Operation class* author Mr.Li* date 2022-12-05*…...

PyTorch 模型性能分析和优化 — 第 1 部分
一、说明 这篇文章的重点将是GPU上的PyTorch培训。更具体地说,我们将专注于 PyTorch 的内置性能分析器 PyTorch Profiler,以及查看其结果的方法之一,即 PyTorch Profiler TensorBoard 插件。 二、深度框架 训练深度学习模型,尤其是…...

Unity3D 简易音频管理器
依赖于Addressable 依赖于单例模板:传送门 using System.Collections.Generic; using System.Security.Cryptography; using System; using UnityEngine; using UnityEngine.AddressableAssets;namespace EasyAVG {public class AudioManager : MonoSingleton<…...

【李沐深度学习笔记】线性回归
课程地址和说明 线性回归p1 本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。 线性回归 如何在美国买房(经典买房预测问题) 一个简化的模型 线性模型 其中, x → [ x 1 , x 2 ,…...
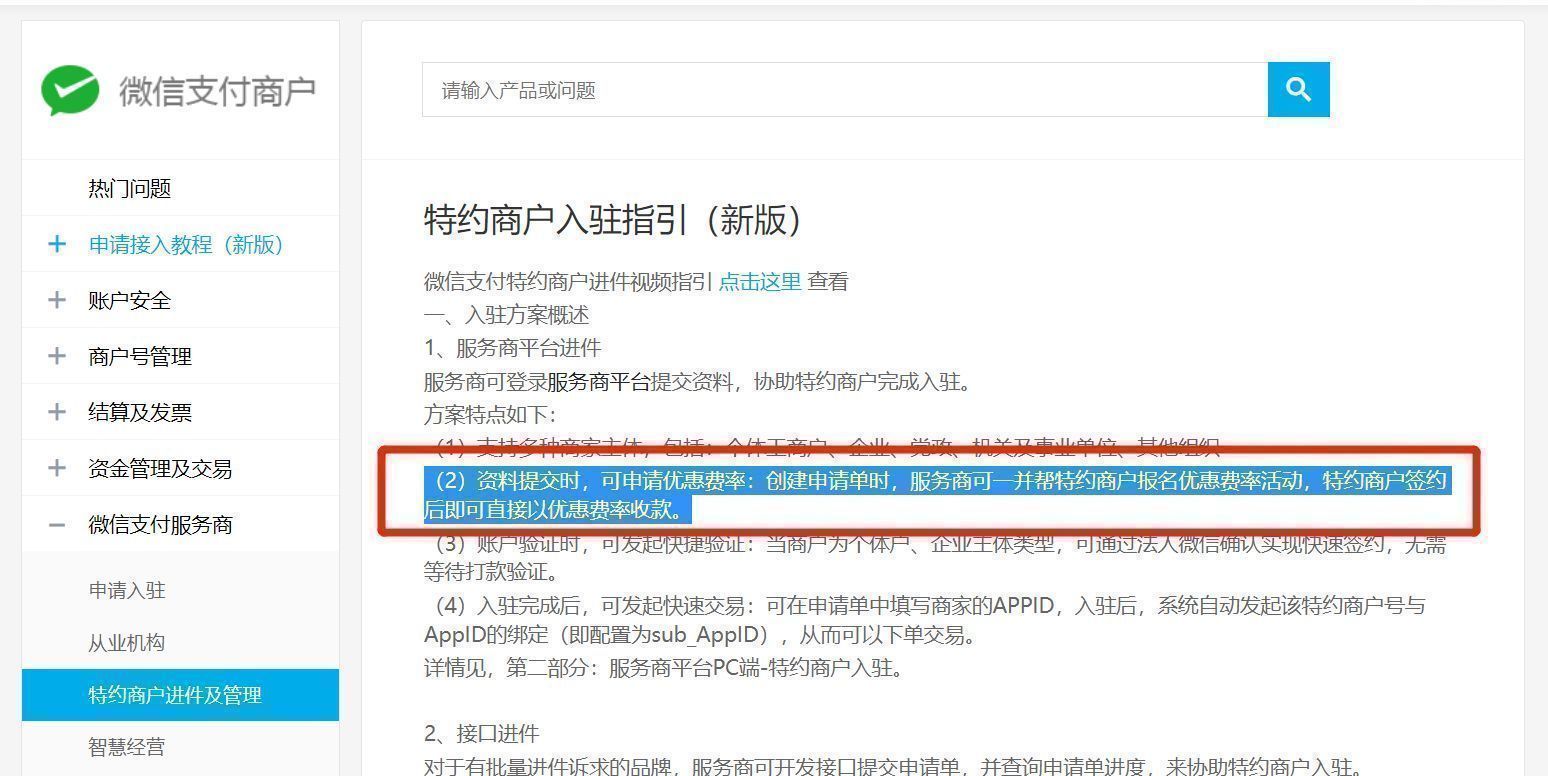
微信收款码费率0.38太坑了
作为一个有多年运营经验的商家,我本人在申请收款功能时曾经走过了不少弯路。我找遍了市面上的知名的支付公司,但了解到的收款手续费率通常都在0.6左右,最低也只能降到0.38。这个过程吃过不少苦头。毕竟,收款功能是我们商家的命脉&…...

【学习笔记】CF1103D Professional layer
首先分析不出啥性质,所以肯定是暴力优化😅 常见的暴力优化手段有均摊,剪枝,数据范围分治(points),答案值域分析之类的。 比较经典的题目是 CF1870E Another MEX Problem,可以用剪枝…...

vue之Pinia
定义 Store | Pinia 开发文档 1.什么是Pinaia Pinia 是 Vue 的专属状态管理库,它允许你跨组件或页面共享状态。 2.理解Pinaia核心概念 定义Store 在深入研究核心概念之前,我们得知道 Store 是用 defineStore() 定义的,它的第一个参数要求是一…...
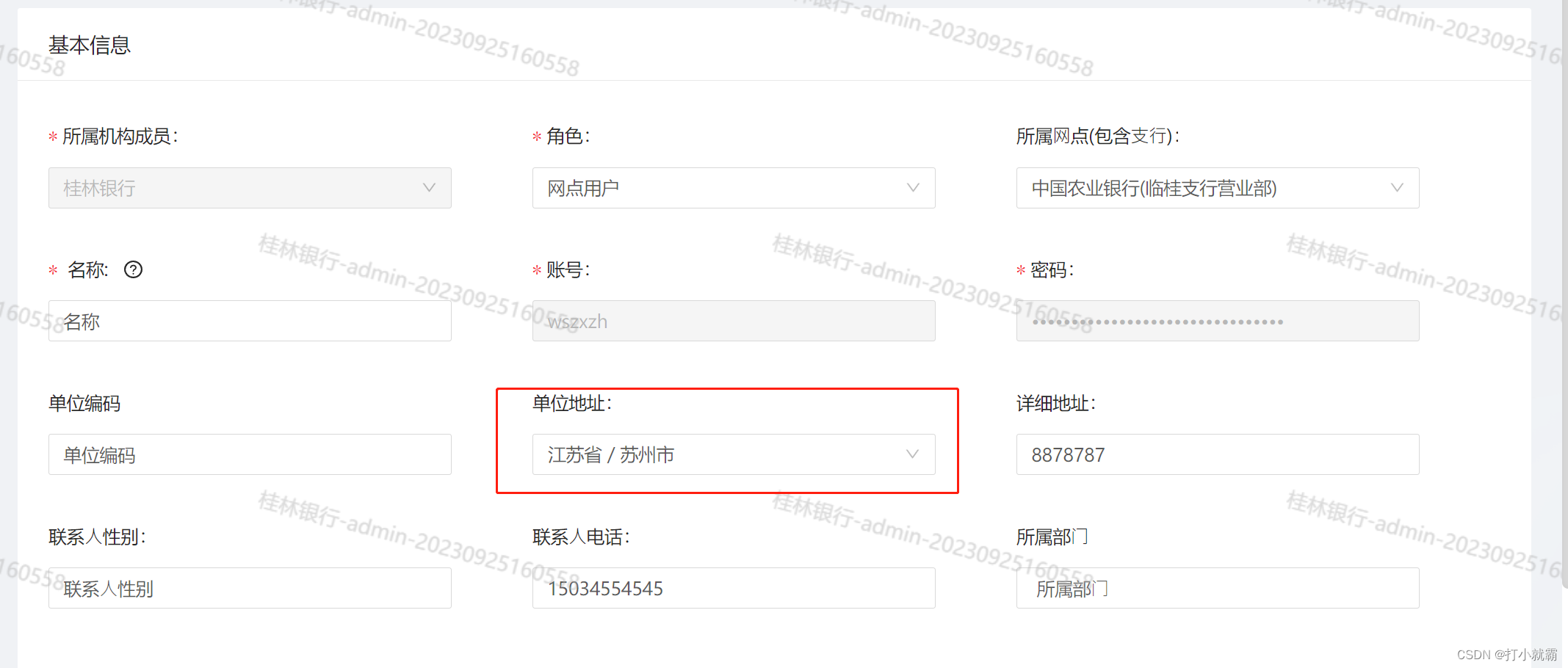
antd-vue 级联选择器默认值不生效解决方案
一、业务场景: 最近在使用Vue框架和antd-vue组件库的时候,发现在做编辑回显时** 级联选择器** 组件的默认值不生效。为了大家后面遇到和我一样的问题,给大家分享一下 二、bug信息: 三、问题原因: 确定不了唯一的值&a…...
分享53个Python源码源代码总有一个是你想要的
分享53个Python源码源代码总有一个是你想要的 链接:https://pan.baidu.com/s/1ew3w2_DXlSBrK7Mybx3Ttg?pwd8888 提取码:8888 项目名称 100-Python ControlXiaomiDevices DRF-ADMIN 后台管理系统 FishC-Python3小甲鱼 Flask框架的api项目脚手架 …...
【每日一题】658. 找到 K 个最接近的元素
658. 找到 K 个最接近的元素 - 力扣(LeetCode) 给定一个 排序好 的数组 arr ,两个整数 k 和 x ,从数组中找到最靠近 x(两数之差最小)的 k 个数。返回的结果必须要是按升序排好的。 整数 a 比整数 b 更接近 …...
)
并发任务队列(字节青训测试题)
需求描述 封装一个并发任务队列类,用于对一些异步任务按指定的并发数量进行并发执行。 /*** 延迟函数* param {number} time - 延迟时间* return {Promise} delayFn - 延迟函数(异步封装)*/ function timeout(time) {return new Promise((resolve) > {setTimeo…...
Ubuntu 安装Nacos
1、官网下载最新版nacos https://github.com/alibaba/nacos/releases 本人环境JDK8,Maven3.6.3,启动Nacos2.2.1启动失败,故切换到2.1.0启动成功 2、放到服务器目录下,我的在/home/xxx/apps下 3、解压 $ tar -zxvf nacos-serve…...

CSS 小球随着椭圆移动
html代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title><…...
【李沐深度学习笔记】线性代数
课程地址和说明 线性代数p1 本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。 线性代数 标量 标量(scalar),亦称“无向量”。有些物理量,只具有数值大小,…...

vuejs - - - - - 递归组件的实现
递归组件的实现 1. 需求描述:2. 效果图:3. 代码3.1 封装组件代码3.2 父组件使用 1. 需求描述: 点击添加行,增加一级目录结构当类型为object or array时,点击右侧➕,增加子集点击右侧🚮&#x…...

精准对接促合作:飞讯受邀参加市工信局举办的企业供需对接会
2023年9月21日,由惠州市工业和信息化局主办的惠州市工业软件企业与制造业企业供需对接会成功举办,对接会旨在促进本地工业软件企业与制造业企业的紧密合作,推动数字化转型的深入发展。此次会议在市工业和信息化局16楼会议室举行,会…...

数学建模之遗传算法
文章目录 前言遗传算法算法思想生物的表示初始种群的生成下一代种群的产生适应度函数轮盘赌交配变异混合产生新种群 停止迭代的条件遗传算法在01背包中的应用01背包问题介绍01背包的其它解法01背包的遗传算法解法生物的表示初始种群的生成下一代种群的产生适应度函数轮盘赌交配…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...
