【笔记】Splay
【笔记】Splay 目录
- 简介
- 右旋
- 左旋
- 核心思想
- 操作
- a. Splay
- b. 插入
- c. 删除
- 信息的维护
- 例题
- AcWing 2437. Splay
- P3369 【模板】普通平衡树
简介
Splay 是一种平衡树,并且是一棵二叉搜索树(BST)。
它满足对于任意节点,都有左子树上任意点的值 < 当前节点的值 < 右子树上任意点的值。
优点:支持多种操作。
缺点:常数较大。
单次操作均摊复杂度 O ( log n ) O(\log n) O(logn)。
(注:关于 Splay 单次操作均摊复杂度的证明见 OI-Wiki)
Splay 基于旋转操作维护树的平衡。旋转分为左旋 (zag) 和右旋 (zig)。
旋转,即在保证平衡树中序遍历不变的前提下,改变整个树的深度。
右旋
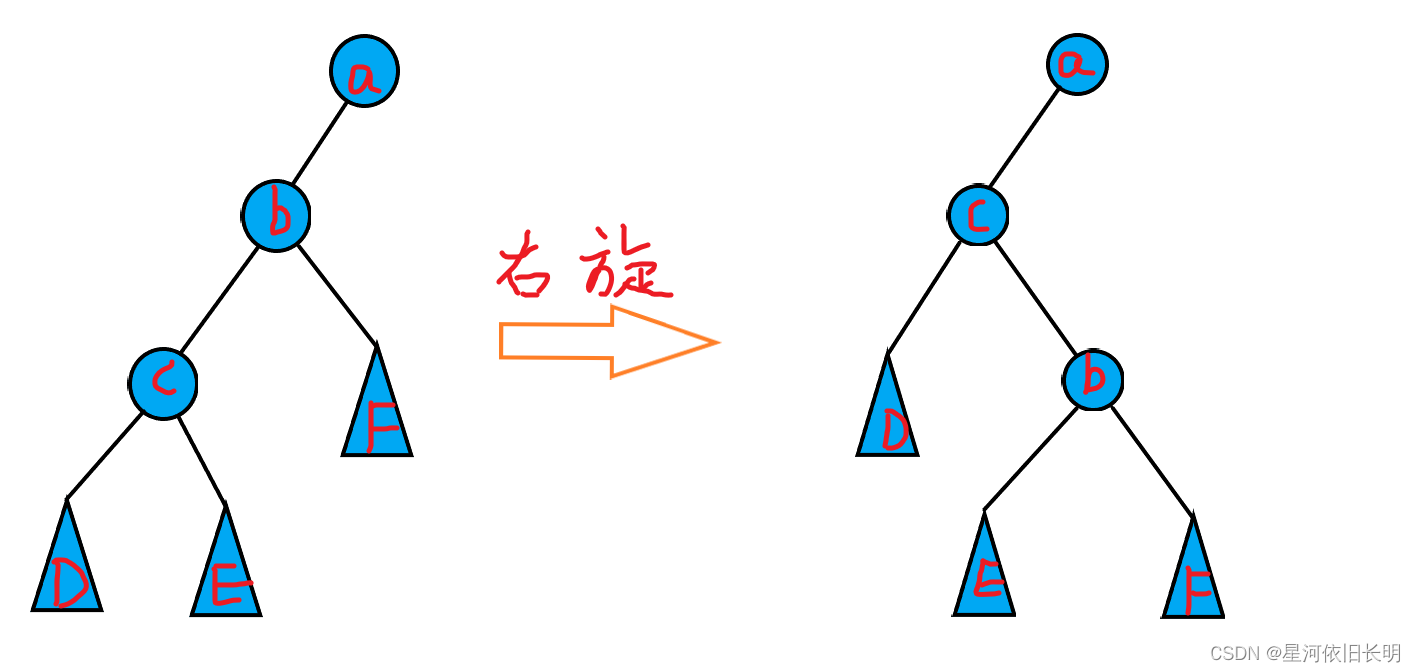
对于单次操作 zig(a) ,将节点 a a a 左儿子的左儿子( c c c)接到 a a a 的左儿子处,将 c c c 的右儿子接到 b b b 的左儿子,将 c c c 的右儿子改为 b b b。
这样,我们完成了一次右旋操作,操作前后, a a a 左子树的中序遍历都为 DcEbF。
左旋
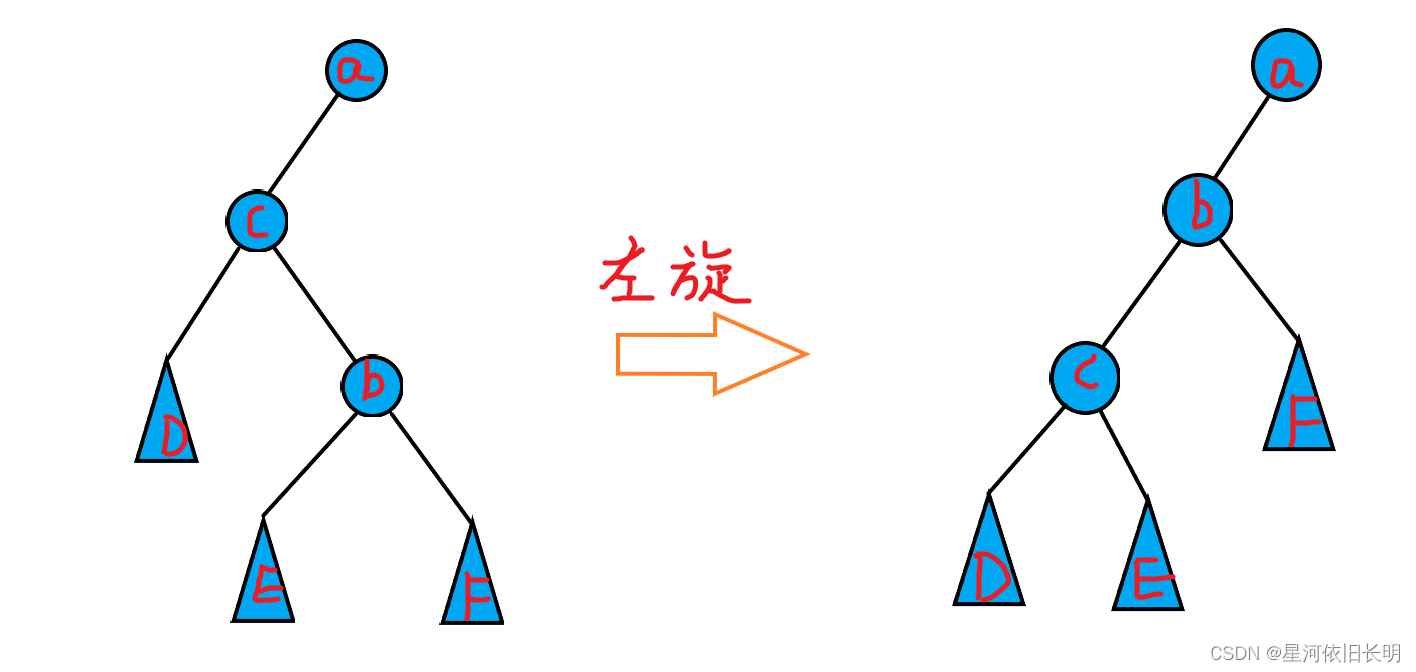
左旋即右旋的逆过程,将每一步反过来即可。
核心思想
每次操作之后,都将被操作的节点旋转至根节点。
这个和均摊时间复杂度有关。
操作
a. Splay
每次调用函数 splay(x, k) 表示把点 x x x 旋转至点 k k k 下方。
特别地,当调用 splay(x, 0) 时,表示把点 x x x 旋转至根节点。
有两种情况:
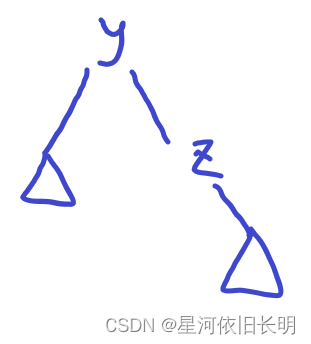
- x , y , z x, y,z x,y,z 成一条链
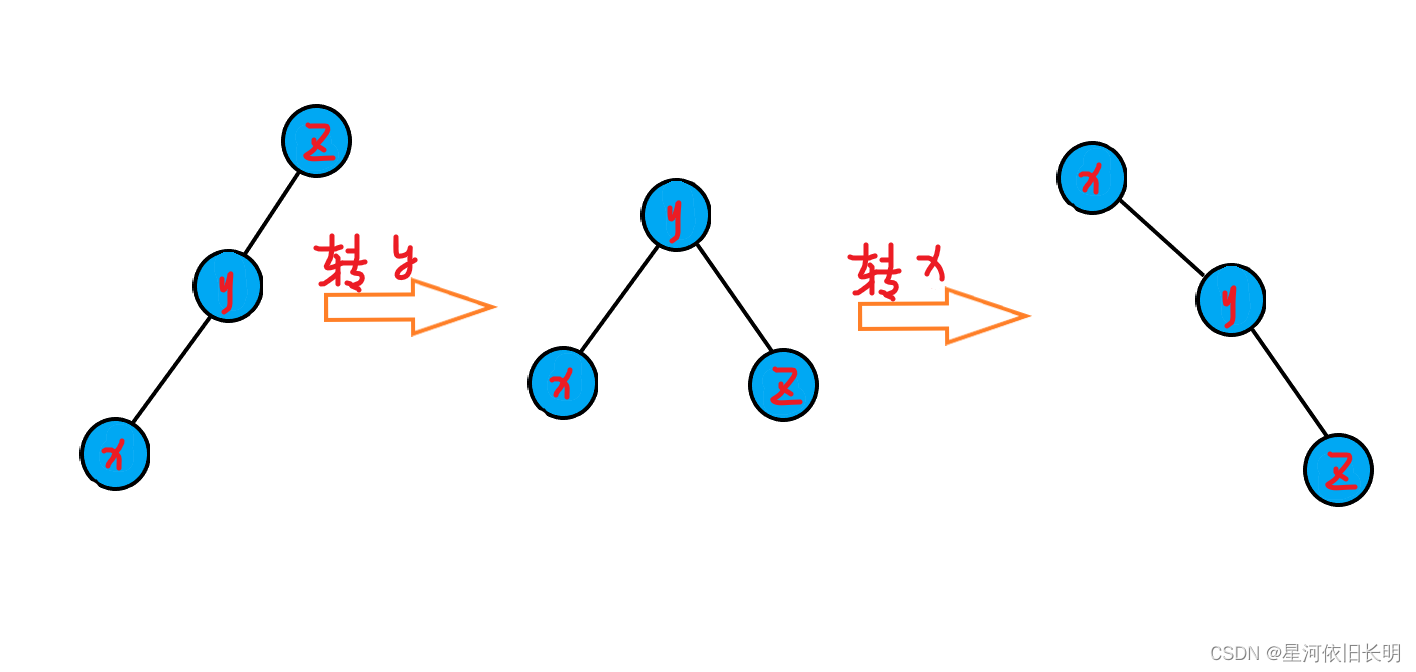
- x , y , z x,y,z x,y,z 不成一条链
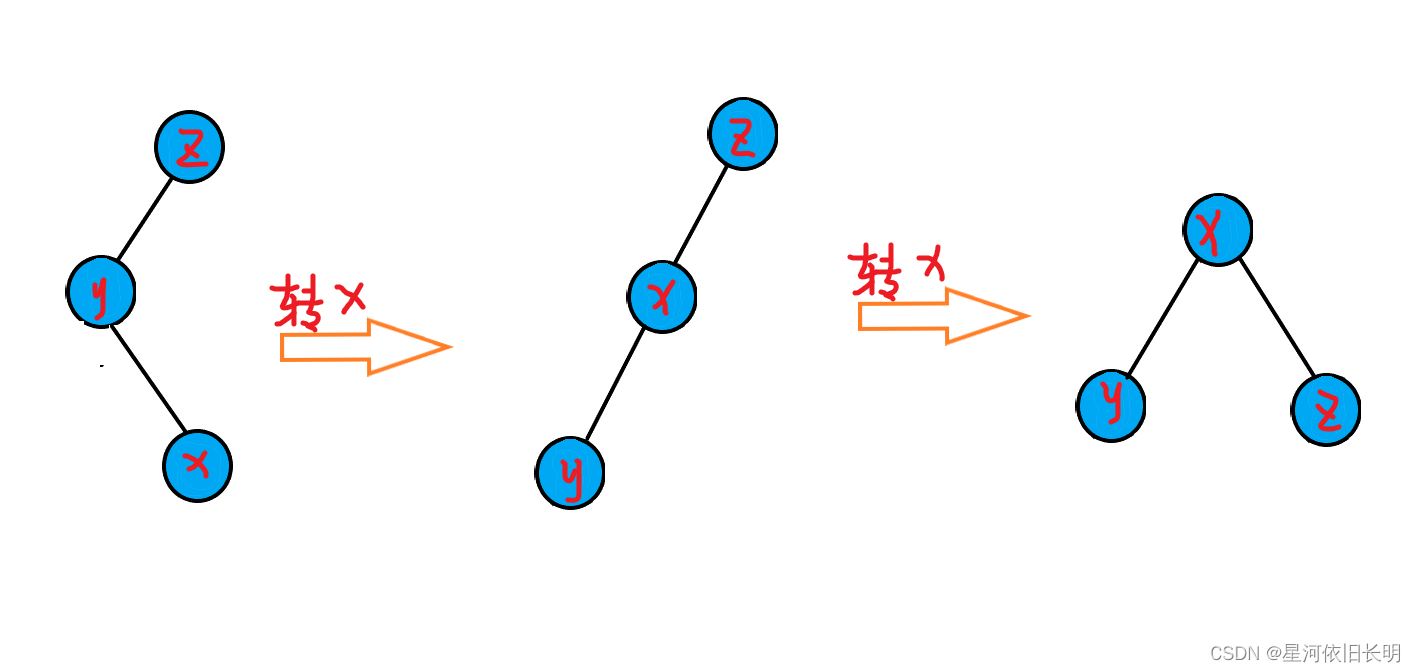
b. 插入
- 根据 BST 性质,找到该元素所在位置并新建节点。插入后将该节点旋转至根节点。
- 当要求将一个序列插到 y y y 的后面时:
- 找到 y y y 的后继 z z z。
- 将 y y y 转到根。(
splay(y, 0);) - 将 z z z 转到 y y y 的下方。(
splay(z, y);)由于 z > y z>y z>y,所以 z z z 是 y y y 的左儿子。 - 显然,此时将要插入的序列接到 z z z 的左儿子(∅)上即可。
c. 删除
- 删除一段区间 [ l , r ] [l,r] [l,r]。
- 分别找到 l l l 的前驱 p p p 和 r r r 的后继 q q q。
- 将 p p p 转到根节点。
- 将 q q q 转到 p p p 下方。由于 p < q p<q p<q,所以 q q q 是 p p p 的左儿子。
- 显然,要删除的区间就是点 p p p 的整个左子树。直接变没即可。


信息的维护
以模板题 AcWing 2437. Splay 为例。
本题要求我们进行区间翻转操作。
因此维护两个值:
- 以每个点为根节点的子树的大小
size。 - 区间翻转懒标记
flag。
和线段树一样,两个函数 pushup 和 pushdown 分别维护 size 和 flag。
本题的 Splay 保证中序遍历是当前序列的顺序,不一定满足 BST 性质。
例题
AcWing 2437. Splay
原题链接
本题仅是插入和翻转两个操作。翻转就是把这个区间所在子树的左右儿子分别翻转。
具体细节看代码。
struct Splay_Node
{int s[2], p; // 左右儿子、父节点int v, size, flag; // 值、子树大小、懒标void init(int _v, int _p) // 初始化{v = _v, p = _p;size = 1;}
}tr[N];int n, m;
int root, idx;void pushup(int u) // 更新当前节点大小
{tr[u].size = tr[tr[u].s[0]].size + tr[tr[u].s[1]].size + 1;
}void pushdown(int u) // 将懒标记下传
{if (tr[u].flag) // 如果当前节点有懒标{swap(tr[u].s[0], tr[u].s[1]); // 就交换左右儿子tr[tr[u].s[0]].flag ^= 1; // 左儿子懒标记更新tr[tr[u].s[1]].flag ^= 1; // 右儿子懒标记更新tr[u].flag ^= 1; // 当前节点懒标记清空}
}void rotate(int x) // 旋转
{int y = tr[x].p, z = tr[y].p; // 当前节点的父亲和祖父int k = tr[y].s[1] == x, kk = tr[z].s[1] == y; // 0 -> left | 1 -> right// 这里一个小技巧判断哪个儿子tr[z].s[kk] = x, tr[x].p = z; // z的儿子改为xtr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y; // y的儿子改为x的反儿子tr[x].s[k ^ 1] = y, tr[y].p = x; // x的反儿子变成ypushup(y), pushup(x); // 更新节点x,y
}void splay(int x, int k)
{while (tr[x].p != k) // 如果k不是当前节点的父节点{int y = tr[x].p, z = tr[y].p; // 当前节点的父亲和祖父if (z != k) // 如果k不是当前节点的祖父if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x); // 不成链先转xelse rotate(y); // 成链先转yrotate(x); // 最后都转一遍x}if (!k) root = x; // 如果当前x是根结点就更新root
}void insert(int v) // 插入
{int u = root, p = 0; // 当前节点和其父节点编号while (u) p = u, u = tr[u].s[v > tr[u].v]; // 只要节点存在就往下找// 后面那句意思是如果插入的值比当前节点小就去左子树,否则去右子树u = ++ idx; // 动态开点编号if (p) tr[p].s[v > tr[p].v] = u; // 如果u不是根结点就更新p的儿子为utr[u].init(v, p); // 初始化新的点usplay(u, 0); // 将u整到根结点
}int kth(int k) // 找第k小数
{int u = root; // 从根结点开始找while (tr[u].size >= k){pushdown(u); // 找之前先下传懒标记if (tr[tr[u].s[0]].size >= k) u = tr[u].s[0]; // 如果k比左子树小的话就去左子树else if (tr[tr[u].s[0]].size + 1 == k) return splay(u, 0), u; // 如果刚好在当前点就返回else k -= tr[tr[u].s[0]].size + 1, u = tr[u].s[1]; // 否则去右子树}return -1; // 找不到就返回-1
}void output(int u) // 输出中序遍历"左-根-右"
{pushdown(u); // 访问之前先下传if (tr[u].s[0]) output(tr[u].s[0]); // 如果左子树存在就遍历左子树if (tr[u].v >= 1 && tr[u].v <= n) printf("%d ", tr[u].v); // 根结点不是哨兵就输出根结点if (tr[u].s[1]) output(tr[u].s[1]); // 如果右子树存在就遍历右子树
}int main()
{scanf("%d%d", &n, &m);for (int i = 0; i <= n + 1; i ++ ) // 多加2哨兵防止越界insert(i);int l, r;while (m -- ){scanf("%d%d", &l, &r);l = kth(l), r = kth(r + 2); // 由于前面加了一个哨兵所以如果我们想要提取区间[l,r]就要以l和r+2分割splay(l, 0), splay(r, l); // 将l转到根节点,将r+2转到根节点下方tr[tr[r].s[0]].flag ^= 1; // 把r+2的左子树打上懒标记}output(root);return 0;
}
P3369 【模板】普通平衡树
原题链接
您需要写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下操作:
- 插入 x x x 数
- 删除 x x x 数(若有多个相同的数,应只删除一个)
- 查询 x x x 数的排名(排名定义为比当前数小的数的个数 + 1 +1 +1 )
- 查询排名为 x x x 的数
- 求 x x x 的前驱(前驱定义为小于 x x x,且最大的数)
- 求 x x x 的后继(后继定义为大于 x x x,且最小的数)
- 插入:根据 BST 的性质,找到这个值所在的节点。如果该节点存在,则将 cnt + 1 \text{cnt}+1 cnt+1。如果不存在就新建一个节点。
- 删除:找到这个值的前驱 prev \text{prev} prev 和后继 next \text{next} next(节点编号),将 prev \text{prev} prev 转到根节点,将 next \text{next} next 转到 prev \text{prev} prev 下方。如果 next \text{next} next 左儿子 cnt > 1 \text{cnt}>1 cnt>1 则将 cnt − 1 \text{cnt}-1 cnt−1,否则直接删除左儿子。
- 根据数值找排名:将该数值对应的节点转到根节点,然后返回左子树的大小 + 1 +1 +1。
- 根据排名找数值:从根结点开始找,如果 k k k 比左子树小的话就去左子树,如果刚好在当前点就把这个点转上去并返回,否则去右子树。
- 求前驱:根据 BST 性质先找出它的位置转到根节点。如果这个值不存在即根节点值小于输入值,则返回根节点值。否则返回根结点左子树的最右儿子。
- 求后继:根据 BST 性质先找出它的位置转到根节点。如果这个值不存在即根节点值大于输入值,则返回根节点值。否则返回根结点右子树的最左儿子。
struct Node
{int size, cnt, v;int p, s[2];void init(int _v, int _p){v = _v, p = _p;size = 1;}
}tr[N];int n;
int root, idx;void pushup(int x) // 更新子树大小
{tr[x].size = tr[tr[x].s[0]].size + tr[tr[x].s[1]].size + tr[x].cnt; // 注意因为值可以重复,所以加cnt
}void rotate(int x) // 旋转
{int y = tr[x].p, z = tr[y].p;int k = tr[y].s[1] == x;tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;tr[x].s[k ^ 1] = y, tr[y].p = x;pushup(y), pushup(x);
}void splay(int x, int k) // 这个可以去翻上面的注释
{while (tr[x].p != k){int y = tr[x].p, z = tr[y].p;if (z != k)if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);else rotate(y);rotate(x);}if (!k) root = x;
}void upper(int v) // 根据BST性质找值v所在的节点并转到根节点
{int u = root; // 从根结点开始while (tr[u].s[v > tr[u].v] && tr[u].v != v) // 如果值比当前节点小就去左子树,否则去右子树u = tr[u].s[v > tr[u].v];splay(u, 0); // 找到之后将这个节点转到根节点// 如果这个值不存在,则显然会返回这个值前驱或后继所在的节点
}int get_prev(int v) // 找前驱
{upper(v); // 转到根节点if (tr[root].v < v) return root; // 如果这个值不存在且根结点值小则根节点就是前驱int u = tr[root].s[0]; // 从左子树开始搜while (tr[u].s[1]) u = tr[u].s[1]; // 左子树最右面return u;
}int get_next(int v) // 找后继
{upper(v); // 转到根节点if (tr[root].v > v) return root; // 如果这个值不存在且根结点值大则根结点就是后继int u = tr[root].s[1]; // 从右子树开始搜while (tr[u].s[0]) u = tr[u].s[0]; // 右子树最左面return u;
}int get_rank_by_val(int v) // 根据数值找排名
{upper(v); // 转到根节点return tr[tr[root].s[0]].size + 1; // 左子树大小+1
}int get_val_by_rank(int k) // 根据排名找数值
{int u = root;while (tr[u].size >= k){if (tr[tr[u].s[0]].size >= k) u = tr[u].s[0];else if (tr[tr[u].s[0]].size + tr[u].cnt >= k) return splay(u, 0), tr[u].v; // 记得把当前点转上去else k -= tr[tr[u].s[0]].size + tr[u].cnt, u = tr[u].s[1];}return -1;
}void insert(int v) // 插入一个值
{int u = root, p = 0;while (u && tr[u].v != v) p = u, u = tr[u].s[v > tr[u].v];if (u) tr[u].cnt ++ ; // 如果这个点已经存在就把cnt+1else{u = ++ idx; // 否则新建一个点if (p) tr[p].s[v > tr[p].v] = u; // 如果新建的不是根结点就更新其父节点的儿子指针tr[u] = {1, 1, v, p}; // 初始化}splay(u, 0);
}void remove(int v) // 移除一个值
{int prev = get_prev(v), next = get_next(v); // 找出前驱和后继splay(prev, 0), splay(next, prev); // 将前驱转到根节点,将后继转到前驱下方int w = tr[next].s[0]; // 后继的左儿子是要删除的值if (tr[w].cnt > 1) tr[w].cnt -- , splay(w, 0); // 如果不止一个就把cnt-1然后转上去else tr[next].s[0] = 0, splay(next, 0); // 否则把next左儿子指针置空然后把后继转上去
}void output(int u)
{if (tr[u].s[0]) output(tr[u].s[0]);if (tr[u].v != -INF && tr[u].v != INF) printf("%d ", tr[u].v);if (tr[u].s[1]) output(tr[u].s[1]);
}int main()
{int op, x;insert(INF), insert(-INF); // 为防止出界整两个哨兵scanf("%d", &n);while (n -- ){scanf("%d%d", &op, &x);switch (op){case 1: insert(x); break;case 2: remove(x); break;case 3: printf("%d\n", get_rank_by_val(x) - 1); break; // 由于有哨兵,所以排名-1case 4: printf("%d\n", get_val_by_rank(x + 1)); break; // 由于有哨兵,所以输入+1case 5: printf("%d\n", tr[get_prev(x)].v); break; // 由于找前驱返回的是下标case 6: printf("%d\n", tr[get_next(x)].v); break; // 所以输出数值}}return 0;
}
最后,如果觉得对您有帮助的话,点个赞再走吧!
相关文章:

【笔记】Splay
【笔记】Splay 目录 简介右旋左旋 核心思想操作a. Splayb. 插入c. 删除 信息的维护例题AcWing 2437. SplayP3369 【模板】普通平衡树 简介 Splay 是一种平衡树,并且是一棵二叉搜索树(BST)。 它满足对于任意节点,都有左子树上任意…...

opencv英文识别tesseract-orc安装
文章目录 一、安装并保存所在路径二、配置环境变量1、打开高级设置2、配置环境变量三、修改tesseract.py文件中的路径,否则运行报错1、进入python所在的文件夹,找到Lib,site-packages2、搜索pytesseract3、打开py文件修改路径一、安装并保存所在路径 特别注意路径名中不能有…...

JNA封装C/C++动态库在flink内使用记录
概述 因为公司业务需求,需要将一部分原本已经用C/C写好的程序封装到flink内部使用。 操作系统 CentOS 7使用的技术和工具 flink 1.17.1 JDK 19.0.2 JNA 5.12.1 maven 3.9.4技术实现 利用JNA将C/C的程序封装到JAR包里面,然后结合flink依赖࿰…...
Android gradle dependency tree change(依赖树变化)监控实现
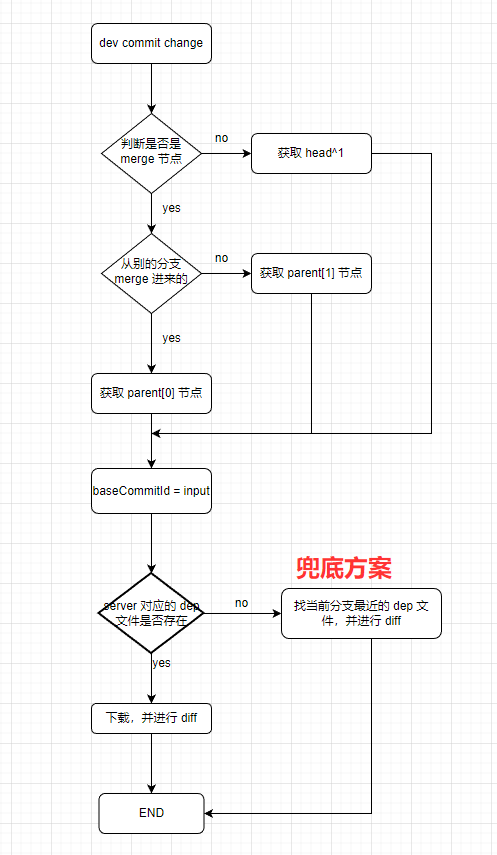
文章目录 前言基本原理执行流程diff 报告不同分支 merge 过来的 diff 报告同个分支产生的 merge 报告同个分支提交的 diff 报告 具体实现原理我们需要监控怎样的 Dendenpency 变化怎样获取 dependency Treeproject.configurations 方式./gradlew dependenciesAsciiDependencyRe…...
5个流程图模板网站,帮你轻松绘制专业流程图
在复杂的项目管理和团队协作中,流程图成为了一个必不可少的工具。从零开始创建流程图可能会很耗时,同时也需要一定的技能。使用模板可以让流程图方便制作又保持高颜值,降低制作的成本,一款模板众多、功能强大、具有丰富编辑工具的…...

【AI视野·今日Robot 机器人论文速览 第四十二期】Wed, 27 Sep 2023
AI视野今日CS.Robotics 机器人学论文速览 Wed, 27 Sep 2023 Totally 48 papers 👉上期速览✈更多精彩请移步主页 Interesting: 📚***Tactile Estimation of Extrinsic Contact,基于触觉的外部接触估计与稳定放置 (from 三菱电机) Daily Robotics Pape…...

后端面试关键问题大总结
一、Java基础 1.HashMap的底层原理 2.说一下List的特点 3.介绍一下Java的基本数据类型 (问到这个问题说明你触碰到面试官的技术能力水平底线了) 二、线程 1.说一下线程的4种创建方式 2.线程池的两种创建方式,包括jdk方式和spring方式 …...

uni-app:实现图片周围的图片按照圆进行展示
效果 代码 <template><view class"position"><view class"circle"><img src"/static/item1.png" class"center-image"><view v-for"(item, index) in itemList" :key"index" class&q…...

Django之视图
一)文件与文件夹 当我们设定好一个Djiango项目时,里面会有着view.py等文件,也就是文件的方式: 那么我们在后续增加app等时,view.py等文件会显得较为臃肿,当然也根据个人习惯,这时我们可以使用…...

【软件工程_设计模式】——为什么要使用设计模式?
what? 什么是设计模式? why? 为什么要使用设计模式? 使用设计模式的原因如下: 提高代码的可读性和可维护性:设计模式是前人根据经验总结出来的,使用设计模式,就相当于是站在了前人的肩膀上。…...

大数据之Kafka
Kafka概述 传统定义:一个分布式的基于发布/订阅模式的消息队列,主要应用于大数据实时处理领域。 最新定义:一个开源的分布式事件流平台,被数千家公司用于高性能数据管道、流分析、数据集成和关键任务应用。最主要的功能是做数据的…...
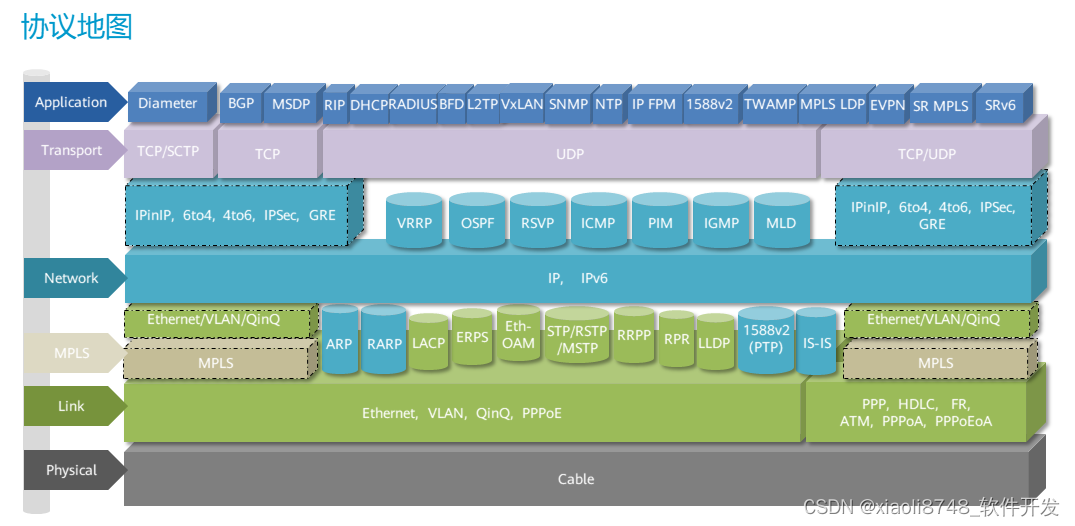
灵活运用OSI模型提升排错能力
1.OSI模型有什么实际价值? 2.二层和三层网络的区别和应用; 3.如何通过OSI模型提升组网排错能力? -- OSI - 开放式系统互联 - OSI参考模型 - 一个互联标准 -- 软件硬件 - 定义标准 数据通信的标准 -- 厂商 思科 华为 华三…...

【最新!企知道AES加密分析】使用Python实现完整解密算法
文章目录 1. 写在前面2. 过debugger3. 抓包分析4. 断点分析5. Python实现解密算法1. 写在前面 最近华为各方面传递出来的消息无不体现出华为科技实力与技术处于遥遥领先的地位。所以出于好奇想要了解一下咱们国内这些互联网科技企业有哪些技术专利,于是就有了这篇文章! 分析目…...

前端架构师之11_JavaScript事件
1 事件处理 1.1 事件概述 在学习事件前,有几个重要的概念需要了解: 事件事件处理程序事件驱动式事件流 事件 可被理解为是JavaScript侦测到的行为。 这些行为指的就是页面的加载、鼠标单击页面、鼠标滑过某个区域等。 事件处理程序 指的就是Java…...

文本过滤工具:grep
什么是grep? grep是一个命令行文本搜索工具,它的名称来源于"Global Regular Expression Print"(全局正则表达式打印)。它的主要功能是在文本文件中查找特定模式或字符串,并将匹配的行打印到终端或输出到文件…...
【Linux】生产者和消费者模型
生产者和消费者概念基于BlockingQueue的生产者消费者模型全部代码 生产者和消费者概念 生产者消费者模式就是通过一个容器来解决生产者和消费者的强耦合问题。 生产者和消费者彼此之间不直接通讯,而通过这个容器来通讯,所以生产者生产完数据之后不用等待…...
开发APP的费用是多少
开发一款APP的费用可以因多种因素而异,包括项目的规模、功能、复杂性、技术选择、地理位置等。北京是中国的大城市,APP开发的费用也会受到北京的物价水平和市场竞争的影响。以下是一些可以影响APP开发费用的因素,希望对大家有所帮助。北京木奇…...
start()方法源码分析
当我们创建好一个线程之后,可以调用.start()方法进行启动,start()方法的内部其实是调用本地的start0()方法, 其实Thread.java这个类中的方法在底层的Thread.c文件中都是一一对应的,在Thread.c中start0方法的底层调用了jvm.cpp文件…...

VUE_history模式下页面404错误
uniapp 的history 把#去掉了,但是当刷新页面的时候出现404错误 解决方案:需要服务端支持 如果 URL 匹配不到任何静态资源,则应该返回同一个 index.html 页面 Apache <IfModule mod_rewrite.c>RewriteEngine OnRewriteBase /RewriteRu…...
现代数据架构-湖仓一体
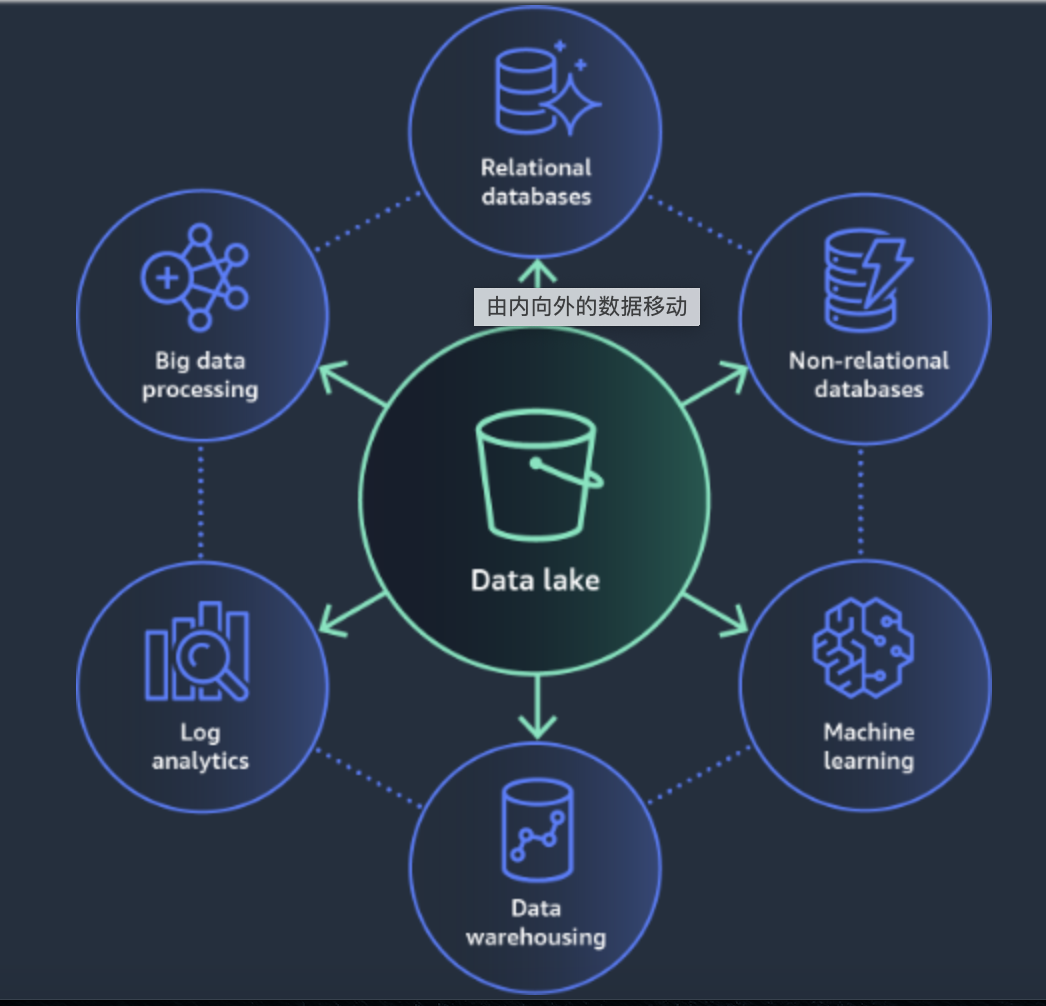
当前的数据架构已经从数据库、数据仓库,发展到了数据湖、湖仓一体架构,本篇文章从头梳理了一下数据行业发展的脉络。 上世纪,最早出现了关系型数据库,也就是DBMS,有商业的Oracle、 IBM的DB2、Sybase、Informix、 微软…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
