LeetCode 周赛上分之旅 #48 一道简单的树上动态规划问题
⭐️ 本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 和 BaguTree Pro 知识星球提问。
学习数据结构与算法的关键在于掌握问题背后的算法思维框架,你的思考越抽象,它能覆盖的问题域就越广,理解难度也更复杂。在这个专栏里,小彭与你分享每场 LeetCode 周赛的解题报告,一起体会上分之旅。
本文是 LeetCode 上分之旅系列的第 48 篇文章,往期回顾请移步到文章末尾~
LeetCode 双周赛 114
T1. 收集元素的最少操作次数(Easy)
- 标签:模拟、散列表
T2. 使数组为空的最少操作次数(Medium)
- 标签:贪心、散列表
T3. 将数组分割成最多数目的子数组(Medium)
- 标签:思维、位运算
T4. 可以被 K 整除连通块的最大数目(Hard)
- 标签:树上 DP
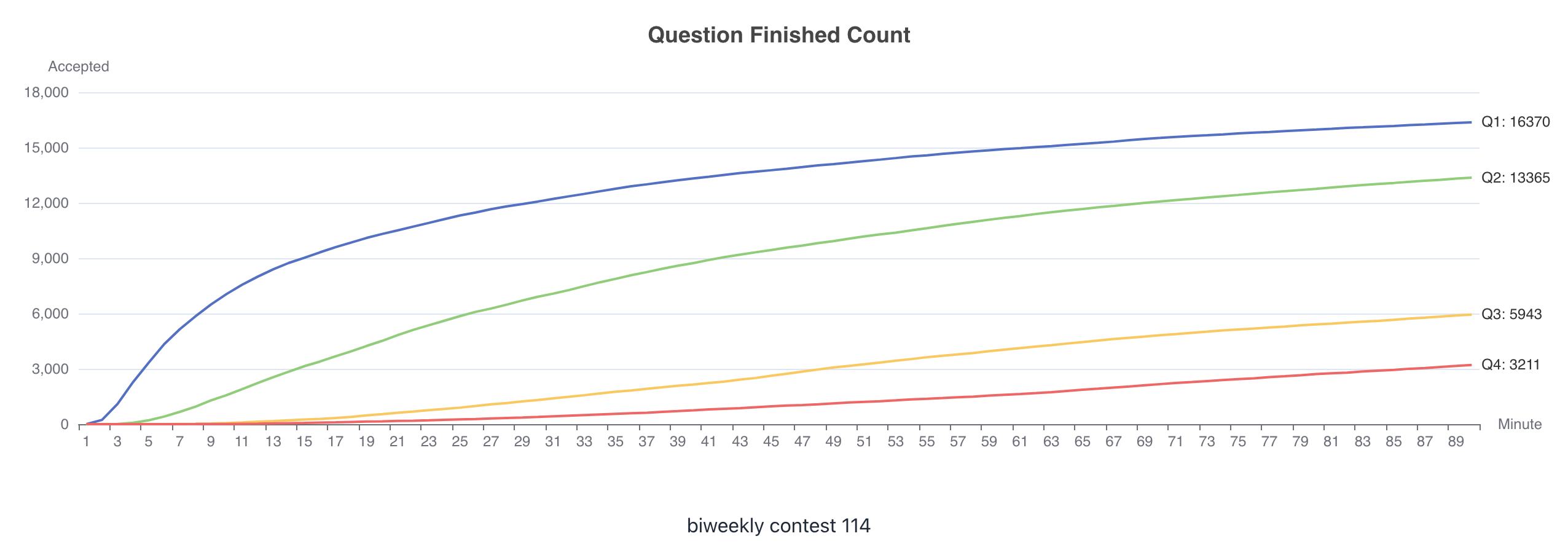
T1. 收集元素的最少操作次数(Easy)
https://leetcode.cn/problems/minimum-operations-to-collect-elements/description/
题解(散列表)
简单模拟题。
预初始化包含 1 − k 1 - k 1−k 元素的集合,根据题意逆向遍历数组并从集合中移除元素,当集合为空时表示已经收集到所有元素,返回 n − i n - i n−i。
class Solution {fun minOperations(nums: List<Int>, k: Int): Int {val n = nums.sizeval set = (1..k).toHashSet()for (i in n - 1 downTo 0) {set.remove(nums[i])if (set.isEmpty()) return n - i}return -1}
}
class Solution:def minOperations(self, nums, k):n, nums_set = len(nums), set(range(1, k+1))for i in range(n-1, -1, -1):nums_set.discard(nums[i])if not nums_set:return n - ireturn -1
class Solution {
public:int minOperations(std::vector<int>& nums, int k) {int n = nums.size();unordered_set<int> set;for (int i = 1; i <= k; ++i) {set.insert(i);}for (int i = n - 1; i >= 0; --i) {set.erase(nums[i]);if (set.empty()) {return n - i;}}return -1;}
};
function minOperations(nums: number[], k: number): number {var n = nums.length;var set = new Set<number>();for (let i = 1; i <= k; ++i) {set.add(i);}for (let i = n - 1; i >= 0; --i) {set.delete(nums[i]);if (set.size === 0) {return n - i;}}return -1;
};
class Solution {int minOperations(List<int> nums, int k) {int n = nums.length;Set<int> set = Set<int>();for (int i = 1; i <= k; i++) {set.add(i);}for (int i = n - 1; i >= 0; i--) {set.remove(nums[i]);if (set.isEmpty) return n - i;}return -1;}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) 线性遍历;
- 空间复杂度: O ( k ) O(k) O(k) 散列表空间。
T2. 使数组为空的最少操作次数(Medium)
https://leetcode.cn/problems/minimum-number-of-operations-to-make-array-empty/description/
题解(贪心)
题目两种操作的前提是数字相等,因此我们先统计每个元素的出现次数。
从最少次数的目标出发,显然能移除 3 3 3 个就尽量移除 3 3 3 个,再分类讨论:
- 如果出现次数为 1 1 1,那么一定无解,返回 − 1 -1 −1;
- 如果出现次数能够被 3 3 3 整除,那么操作 c n t / 3 cnt / 3 cnt/3 次是最优的;
- 如果出现次数除 3 3 3 余 1 1 1,那么把 1 1 1 个 3 3 3 拆出来合并为 4,操作 c n t / 3 + 1 cnt / 3 + 1 cnt/3+1 次是最优的;
- 如果出现次数除 3 3 3 余 2 2 2,那么剩下的 2 2 2 操作 1 1 1 次,即操作 c n t / 3 + 1 cnt / 3 + 1 cnt/3+1 次是最优的。
组合以上讨论:
class Solution {fun minOperations(nums: IntArray): Int {val cnts = HashMap<Int, Int>()for (e in nums) {cnts[e] = cnts.getOrDefault(e, 0) + 1}var ret = 0for ((_, cnt) in cnts) {if (cnt == 1) return -1when (cnt % 3) {0 -> {ret += cnt / 3}1, 2 -> {ret += cnt / 3 + 1}}}return ret}
}
继续挖掘题目特性,对于余数大于 0 0 0 的情况总是 向上取整 ,那么可以简化为:
class Solution {fun minOperations(nums: IntArray): Int {val cnts = HashMap<Int, Int>()for (e in nums) {cnts[e] = cnts.getOrDefault(e, 0) + 1}var ret = 0for ((_, cnt) in cnts) {if (cnt == 1) return -1ret += (cnt + 2) / 3 // 向上取整}return ret}
}
class Solution:def minOperations(self, nums: List[int]) -> int:cnts = Counter(nums)ret = 0for cnt in cnts.values():if cnt == 1: return -1ret += (cnt + 2) // 3return ret
class Solution {
public:int minOperations(std::vector<int>& nums) {unordered_map<int, int> cnts;for (auto &e : nums) {cnts[e] += 1;}int ret = 0;for (auto &p: cnts) {if (p.second == 1) return -1;ret += (p.second + 2) / 3;}return ret;}
};
function minOperations(nums: number[]): number {let cnts: Map<number, number> = new Map<number, number>();for (let e of nums) {cnts.set(e, (cnts.get(e) ?? 0) + 1);}let ret = 0;for (let [_, cnt] of cnts) {if (cnt == 1) return -1;ret += Math.ceil(cnt / 3);}return ret;
};
class Solution {int minOperations(List<int> nums) {Map<int, int> cnts = {};for (int e in nums) {cnts[e] = (cnts[e] ?? 0) + 1;}int ret = 0;for (int cnt in cnts.values) {if (cnt == 1) return -1;ret += (cnt + 2) ~/ 3; // 向上取整}return ret;}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) 线性遍历
- 空间复杂度: O ( n ) O(n) O(n) 计数空间。
T3. 将数组分割成最多数目的子数组(Medium)
https://leetcode.cn/problems/split-array-into-maximum-number-of-subarrays/description/
题解(思维题)
一个重要的结论是:当按位与的数量增加时,按位与的结果是非递增的。
题目要求在子数组的按位与的和最小的前提下,让子数组的个数最大。根据上面的结论,显然将数组全部按位与是最小的。
分类讨论:
- 如果整体按位于的结果不为 0 0 0,那么就不可能存在分割数组的方法使得按位与的和更小,直接返回 1 1 1;
- 否则,问题就变成分割数组的最大个数,使得每个子数组按位与为 0 0 0,直接贪心分割就好了。
class Solution {fun maxSubarrays(nums: IntArray): Int {val mn = nums.reduce { acc, it -> acc and it }if (mn > 0) return 1 // 特判var ret = 0var cur = Integer.MAX_VALUEfor (i in nums.indices) {cur = cur and nums[i]if (cur == 0) {cur = Integer.MAX_VALUEret++}}return ret }
}
class Solution:def maxSubarrays(self, nums: List[int]) -> int:if reduce(iand, nums): return 1ret, mask = 0, (1 << 20) - 1cur = maskfor num in nums:cur &= numif cur == 0: ret += 1; cur = maskreturn ret
class Solution {
public:int maxSubarrays(vector<int>& nums) {int mn = nums[0];for (auto num : nums) mn &= num;if (mn != 0) return 1;int ret = 0;int cur = INT_MAX;for (int i = 0; i < nums.size(); i++) {cur &= nums[i];if (cur == 0) {cur = INT_MAX;ret++;}}return ret;}
};
function maxSubarrays(nums: number[]): number {const n = nums.length;let mn = nums.reduce((acc, it) => acc & it);if (mn > 0) return 1; // 特判let mask = (1 << 20) - 1let ret = 0;let cur = mask;for (let i = 0; i < n; i++) {cur = cur & nums[i];if (cur === 0) {cur = mask;ret++;}}return ret;
};
class Solution {int maxSubarrays(List<int> nums) {var mn = nums.reduce((acc, it) => acc & it);if (mn > 0) return 1; // 特判var mask = (1 << 20) - 1;var ret = 0;var cur = mask;for (var i = 0; i < nums.length; i++) {cur = cur & nums[i];if (cur == 0) {cur = mask;ret++;}}return ret;}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) 线性遍历;
- 空间复杂度: O ( 1 ) O(1) O(1) 仅使用常量级别空间。
T4. 可以被 K 整除连通块的最大数目(Hard)
https://leetcode.cn/problems/maximum-number-of-k-divisible-components/
问题分析
初步分析:
- 问题目标: 求解分割后满足条件的最大连通块数量;
- 问题条件: 连通块的和能够被 K 整除;
- 关键信息: 题目保证数据是可以分割的,这是重要的前提。
思考实现:
在保证问题有解的情况下,树上的每个节点要么是单独的连通分量,要么与邻居组成连通分量。那么,这就是典型的「连或不连」和「连哪个」动态规划思维。
- 思考「连或不连」:
如果节点 A A A 的价值能够被 K K K 整除,那么节点 A A A 能作为单独的连通分量吗?
不一定,例如 K = 3 K = 3 K=3 且树为 1 − 3 − 5 1 - 3 - 5 1−3−5 的情况,连通分量只能为 1 1 1,因为 3 3 3 左右子树都不能构造合法的连通块,因此需要与 3 3 3 连接才行。
- 继续思考「连哪个」:
那么,节点 A A A 应该与谁相连呢?对于节点 A A A 的某个子树 T r e e i Tree_i Treei 来说,存在 2 2 2 种情况:
- 能整除:那么子树 T r e e i Tree_i Treei 不需要和节点 A A A 相连;
- 不能整除:那么子树 T r e e i Tree_i Treei 的剩余值就必须与节点 A A A 相连,有可能凑出 K K K 的整除。
当节点 A A A 与所有子树的剩余值组合后,再加上当前节点的价值,如果能够构造出 K K K 的整数倍时,说明找到一个新的连通块,并且不需要和上一级节点组合。否则,则进入不能整除的条件,继续和上一级节点组合。
题解(DFS)
- 定义 DFS 函数并返回两个数值:<子树构造的连通分量, 剩余值>;
- 任意选择一个节点为根节点走一遍 DFS,最终返回 d f s ( 0 , − 1 ) [ 0 ] dfs(0,-1)[0] dfs(0,−1)[0]。
class Solution {fun maxKDivisibleComponents(n: Int, edges: Array<IntArray>, values: IntArray, k: Int): Int {// 建图val graph = Array(n) { LinkedList<Int>() }for ((u, v) in edges) {graph[u].add(v)graph[v].add(u)}// DFS <cnt, left>fun dfs(i: Int, pre: Int): IntArray {var ret = intArrayOf(0, values[i])for (to in graph[i]) {if (to == pre) continueval (childCnt, childLeft) = dfs(to, i)ret[0] += childCntret[1] += childLeft}if (ret[1] % k == 0) {ret[0] += 1ret[1] = 0}return ret}return dfs(0, -1)[0]}
}
class Solution:def maxKDivisibleComponents(self, n, edges, values, k):# 建图graph = defaultdict(list)for u, v in edges:graph[u].append(v)graph[v].append(u)# DFS <cnt, left>def dfs(i, pre):ret = [0, values[i]]for to in graph[i]:if to == pre: continuechildCnt, childLeft = dfs(to, i)ret[0] += childCntret[1] += childLeftif ret[1] % k == 0:ret[0] += 1ret[1] = 0return retreturn dfs(0, -1)[0]
class Solution {
public:int maxKDivisibleComponents(int n, vector<vector<int>>& edges, vector<int>& values, int k) {// 建图vector<list<int>> graph(n);for (auto& edge : edges) {int u = edge[0];int v = edge[1];graph[u].push_back(v);graph[v].push_back(u);}// DFS <cnt, left>function<vector<int>(int, int)> dfs = [&](int i, int pre) -> vector<int> {vector<int> ret(2, 0);ret[1] = values[i];for (int to : graph[i]) {if (to == pre) continue;vector<int> child = dfs(to, i);ret[0] += child[0];ret[1] += child[1];}if (ret[1] % k == 0) {ret[0] += 1;ret[1] = 0;}return ret;};return dfs(0, -1)[0];}
};
function maxKDivisibleComponents(n: number, edges: number[][], values: number[], k: number): number {// 建图let graph = Array(n).fill(0).map(() => []);for (const [u, v] of edges) {graph[u].push(v);graph[v].push(u);}// DFS <cnt, left>let dfs = (i: number, pre: number): number[] => {let ret = [0, values[i]];for (let to of graph[i]) {if (to === pre) continue;let [childCnt, childLeft] = dfs(to, i);ret[0] += childCnt;ret[1] += childLeft;}if (ret[1] % k === 0) {ret[0] += 1;ret[1] = 0;}return ret;};return dfs(0, -1)[0];
};
class Solution {int maxKDivisibleComponents(int n, List<List<int>> edges, List<int> values, int k) {// 建图List<List<int>> graph = List.generate(n, (_) => []);for (final edge in edges) {int u = edge[0];int v = edge[1];graph[u].add(v);graph[v].add(u);}// DFS <cnt, left>List<int> dfs(int i, int pre) {List<int> ret = [0, values[i]];for (int to in graph[i]) {if (to == pre) continue;List<int> child = dfs(to, i);ret[0] += child[0];ret[1] += child[1];}if (ret[1] % k == 0) {ret[0] += 1;ret[1] = 0;}return ret;}return dfs(0, -1)[0];}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) 每个节点访问 1 1 1 次;
- 空间复杂度: O ( n ) O(n) O(n) 图空间。
推荐阅读
LeetCode 上分之旅系列往期回顾:
- LeetCode 单周赛第 364 场 · 前后缀分解结合单调栈的贡献问题
- LeetCode 单周赛第 363 场 · 经典二分答案与质因数分解
- LeetCode 双周赛第 113 场 · 精妙的 O(lgn) 扫描算法与树上 DP 问题
- LeetCode 双周赛第 112 场 · 计算机科学本质上是数学吗?
⭐️ 永远相信美好的事情即将发生,欢迎加入小彭的 Android 交流社群~

相关文章:

LeetCode 周赛上分之旅 #48 一道简单的树上动态规划问题
⭐️ 本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 和 BaguTree Pro 知识星球提问。 学习数据结构与算法的关键在于掌握问题背后的算法思维框架,你的思考越抽象,它能覆盖的问题域就越广,理解难度…...

mysql报错:Column Count Doesn‘t Match Value Count at Row 1
mysql中执行insert、update、delete报错:Column Count Doesnt Match Value Count at Row 1 的解决方案 通常情况:字段不匹配 如:student有id, name, age字段 -- 错误写法 INSERT INTO student VALUES(5,horse)-- 正确写法 INSERT INTO stu…...
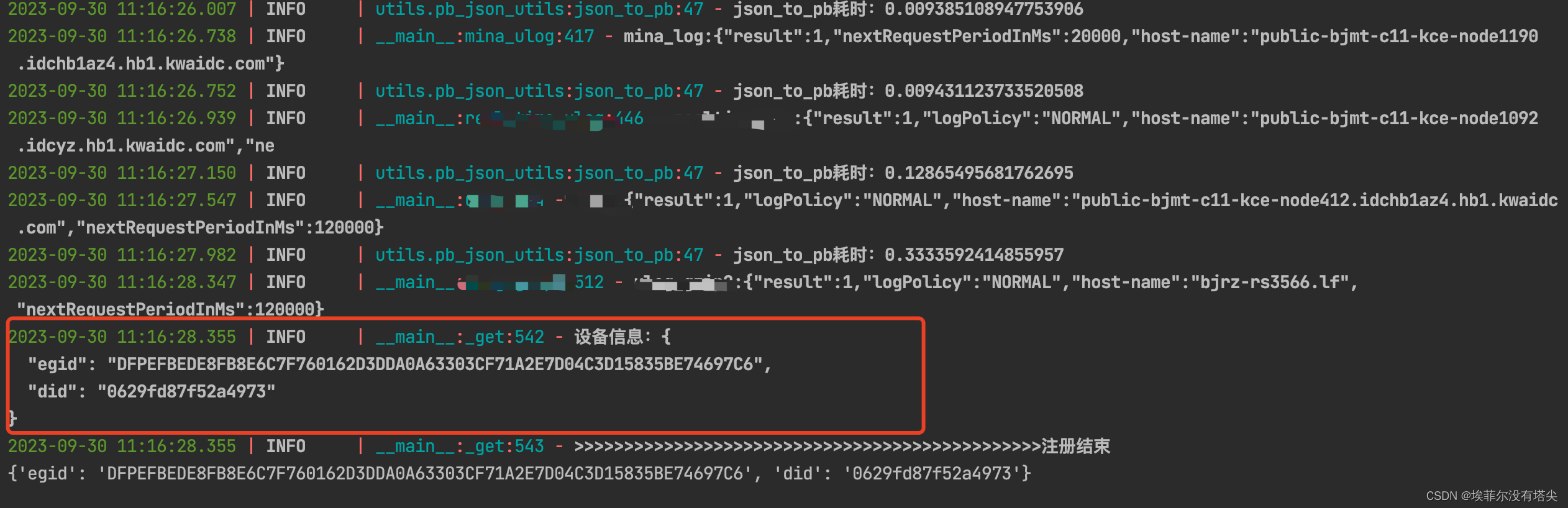
安卓 kuaishou 设备did和egid 学习分析
did和egid注册 接口 https://gdfp.ksapisrv.com/rest/infra/gdfp/report/kuaishou/android did 是本地生成的16进制 或者 获取的 android_id public static final Random f16237a new Random(System.currentTimeMillis()); public static long m19668a() { return f1623…...

基于Vue+ELement实现增删改查案例与表单验证(附源码)
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《ELement》。🎯🎯 …...

webpack:使用externals配置来排除打包后的某个依赖插件IgnorePlugin的使用
背景 假设,我们写了一个库并使用 webpack 打包输出 bundle,但是这个库依赖一个第三方包,比如依赖 lodash,这时候我们不想把这个库打包进 bundle 里因为体积会变大,而且我们的主项目里已经安装了这个 lodash࿰…...
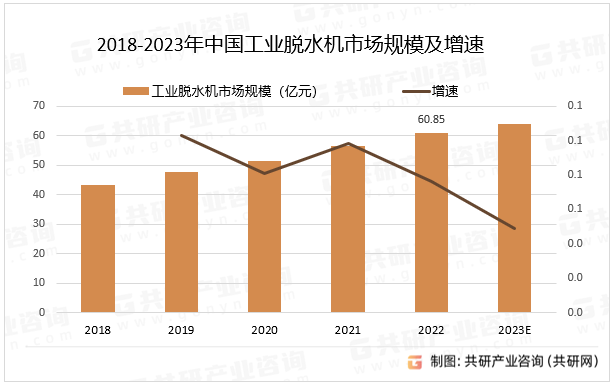
2023年中国工业脱水机行业供需分析:随着自动化和智能化技术的快速发展,销量同比增长4.9%[图]
工业脱水机行业是指专门从湿润的固体物料中去除水分的设备制造和相关服务。它广泛应用于食品加工、化工、制药、纺织、环保等行业,用于去除物料中的水分,提高产品质量和降低能耗。 工业脱水机行业分类 资料来源:共研产业咨询(共研…...

[论文笔记]MacBERT
引言 今天带来MacBERT的阅读笔记。论文题目是 重新审视中文自然语言处理的预训练模型。 本篇主要是探讨中文预训练语言模型在非英文语言中的有效性,然后提出了一种简单而有效的模型,称为MacBERT,它在多个方面改进了RoBERTa,特别是采用纠错型掩码语言模型(MLM as correcti…...

AI发展目前最大挑战是什么?
影响AI成本的因素包括多个方面: 首先,AI技术的复杂性是其成本高昂的一个重要原因。AI技术需要进行大量数据处理、模型训练和优化,这需要耗费大量的计算资源和时间。同时,AI技术需要高水平的专业人才进行设计、开发和维护…...

自然语言处理NLP:LTP、SnowNLP、HanLP 常用NLP工具和库对比
文章目录 常见NLP任务常见NLP工具英文NLP工具中文NLP工具 常见NLP任务 Word Segmentation 分词 – Tokenization Stem extraction 词干提取 - Stemming Lexical reduction 词形还原 – Lemmatization Part of Speech Tagging 词性标注 – Parts of Speech Named entity rec…...
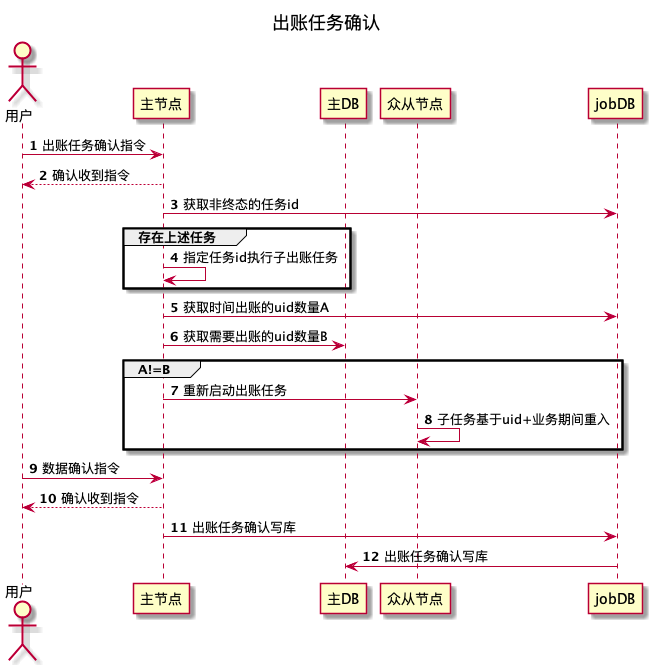
百度交易中台之内容分润结算系统架构浅析
作者 | 交易中台团队 导读 随着公司内容生态的蓬勃发展,内容产出方和流量提供方最关注的“收益结算”的工作,也就成为重中之重。本文基于内容分润结算业务为入口,介绍了实现过程中的重难点,比如千万级和百万级数据量下的技术选型和…...

【索引】常见的索引、B+树结构、什么时候需要使用索引、优化索引方法、索引主要的数据结构、聚簇索引、二级索引、创建合适的索引等重点知识汇总
目录 索引的分类 什么时候需要 / 不需要创建索引? 有什么优化索引的方法 MySQL索引主要使用的两种数据结构是什么 为什么 MySQL 采用 B 树作为索引 聚簇索引和二级索引 根据给定的表,如何创建索引比较好 索引的分类 普通索引:最基本的…...

Egg 封装接口返回信息
中间件封装 代码 const msgArr {"200":成功,"401":token失效 } module.exports (option, app) > {return async function(ctx, next) {try{//成功是返回的信息ctx.emit(code,data,msg)>{console.log(1111,code,data,msg)ctx.body {code,data:dat…...
)
Android AMS——创建APP进程(五)
接上一篇,在 ActivityTaskSupervisor 中会判断进程是否存在,如果进程不存在,则会创建进程,执行 startProcessAsync() 方法。如果进程存在,则执行 realStartActivityLocked() 方法。在APP 的启动时,进程是不存在的。所以我们先来分析一下进程不存在的情况。 一、创建进程…...
凉鞋的 Unity 笔记 102. 场景层次 与 GameObject 的增删改查
102. 场景层次 与 GameObject 的增删改查 在上一篇,我们完成了 Unity 引擎的 Hello world 输出,并且完成了第一个基本循环: 通过这次基本循环的完成,我们获得了一点点的 Unity 使用经验,这非常重要。 有实践经验后再…...
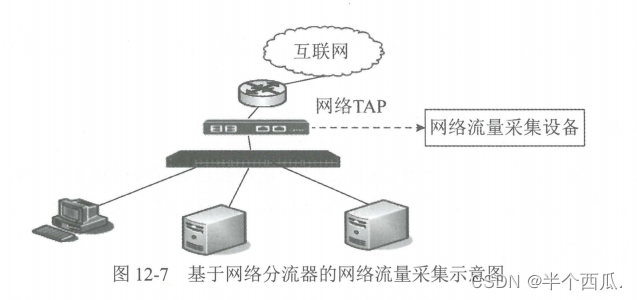
信息安全:网络安全审计技术原理与应用.
信息安全:网络安全审计技术原理与应用. 网络安全审计是指对网络信息系统的安全相关活动信息进行获取、记录、存储、分析和利用的工作。网络安全审计的作用在于建立“事后“安全保障措施,保存网络安全事件及行为信息,为网络安全事件分析提供线…...

嵌入式Linux应用开发-第十三章APP怎么读取按键值
嵌入式Linux应用开发-第十三章读取按键及按键驱动程序 第十三章 APP怎么读取按键值13.1 妈妈怎么知道孩子醒了13.2 APP读取按键的4种方法13.2.1 查询方式13.2.2 休眠-唤醒方式13.2.3 poll方式13.2.4 异步通知方式13.2.4.1 异步通知的原理:发信号13.2.4.2 应用程序之…...

Web 中间件怎么玩?
本次主要是聊聊关于 web 中间件, 分为如下四个方面 什么是 web 框架中间件 为什么要使用 web 中间件 如何使用及其原理 哪些场景需要使用中间件 开门见山 web 中间件是啥 Web 框架中的中间件主要指的是在 web 请求到具体路由之前或者之后,会经过一个或…...
)
HMTL知识点系列(4)
目录 1. 在你过去的项目中,你如何解决HTML的布局和样式问题?2. 你能否解释一下HTML的“文档对象模型”(DOM)是什么,以及它的重要性?3. 你有没有经验处理网页的兼容性问题,特别是在不同浏览器之间…...

CFS内网穿透靶场实战
一、简介 不久前做过的靶场。 通过复现CFS三层穿透靶场,让我对漏洞的利用,各种工具的使用以及横向穿透技术有了更深的理解。 一开始nmap探测ip端口,直接用thinkphpv5版本漏洞工具反弹shell,接着利用蚁剑对服务器直接进行控制,留下…...
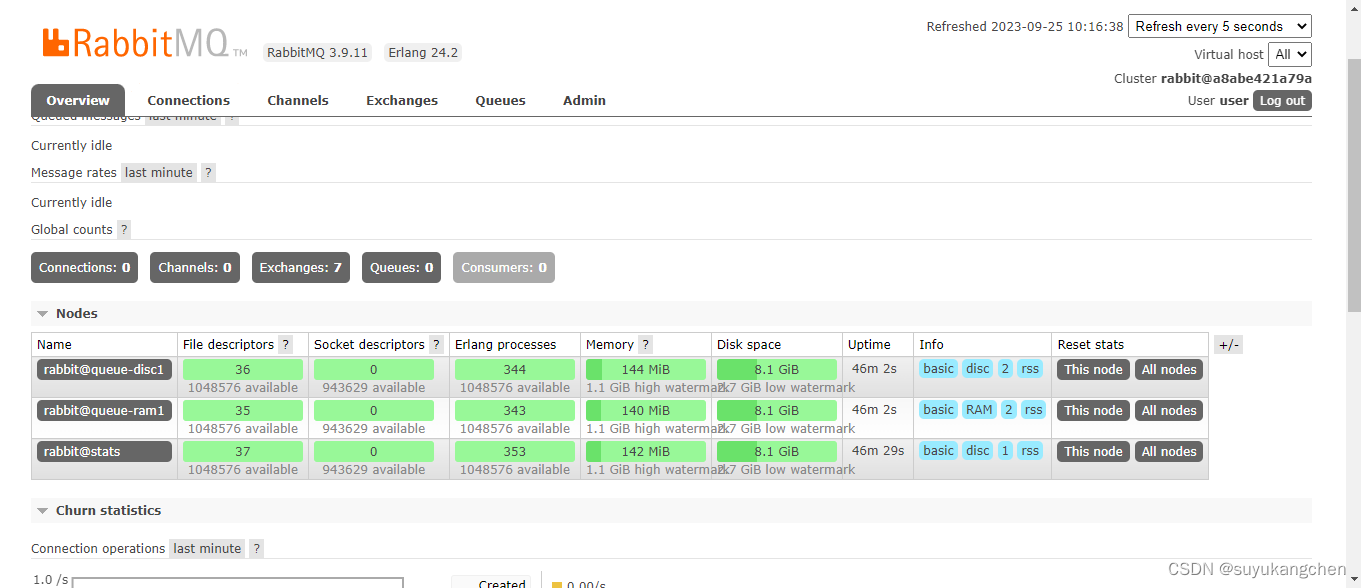
【RabbitMQ实战】07 3分钟部署一个RabbitMQ集群
一、集群的安装部署 我们还是利用docker来安装RabbitMQ集群。3分钟安装一个集群,开始。 前提条件,docker安装了docker-compose。如果没安装的话,参考这里 docker-compose文件参考bitnami官网:https://github.com/bitnami/contai…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...
