cf 解题报告 01
E. Power of Points
Problem - 1857E - Codeforces
题意:
给你 n n n 个点,其整数坐标为 x 1 , … x n x_1,\dots x_n x1,…xn,它们位于一条数线上。
对于某个整数 s s s,我们构建线段[ s , x 1 s,x_1 s,x1], [ s , x 2 s,x_2 s,x2], … \dots …,[ s , x n s,x_n s,xn]。注意,如果是KaTeX parse error: Expected 'EOF', got '&' at position 4: x_i&̲lt;s,那么线段看起来就像[ x i , s x_i,s xi,s]。线段[ a , b a, b a,b] 覆盖了所有的整数点 a , a + 1 , a + 2 , … , b a, a+1, a+2, \dots, b a,a+1,a+2,…,b。
我们把点 p p p 的幂定义为与坐标 p p p 的点相交的线段数,记为 f p f_p fp。
你的任务是计算每个 s ∈ { x 1 , … , x n } s \in \{x_1,\dots,x_n\} s∈{x1,…,xn} 的 ∑ p = 1 1 0 9 f p \sum\limits_{p=1}^{10^9}f_p p=1∑109fp ,即从 1 1 1 到 1 0 9 10^9 109 所有整数点的 f p f_p fp 之和。
例如,如果初始坐标为 [ 1 , 2 , 5 , 7 , 1 ] [1,2,5,7,1] [1,2,5,7,1],我们选择 s = 5 s=5 s=5,那么线段将是 [ 1 , 5 ] [1,5] [1,5], [ 2 , 5 ] [2,5] [2,5], [ 5 , 5 ] [5,5] [5,5], [ 5 , 7 ] [5,7] [5,7], [ 1 , 5 ] [1,5] [1,5].这些点的幂将是 f 1 = 2 , f 2 = 3 , f 3 = 3 , f 4 = 3 , f 5 = 5 , f 6 = 1 , f 7 = 1 , f 8 = 0 , … , f 1 0 9 = 0 f_1=2, f_2=3, f_3=3, f_4=3, f_5=5, f_6=1, f_7=1, f_8=0, \dots, f_{10^9}=0 f1=2,f2=3,f3=3,f4=3,f5=5,f6=1,f7=1,f8=0,…,f109=0.它们的和为 2 + 3 + 3 + 3 + 5 + 1 + 1 = 18 2+3+3+3+5+1+1=18 2+3+3+3+5+1+1=18。
思路:说了这么多就是对每个xi求一个值,这个值得定义是:
∑ i n ( ∣ p − x i ∣ + 1 ) \sum_i^n( | p - x_i| + 1) i∑n(∣p−xi∣+1)
带绝对值不好计算。取绝对值之后就有两种。
p > xi
∑ i k ( p − x i + 1 ) = k ∗ p − ∑ i k ( x i ) − k \sum_i^k(p - x_i + 1) = k * p - \sum_i^k(x_i) - k i∑k(p−xi+1)=k∗p−i∑k(xi)−k
p < xi
∑ i k ( x i − p + 1 ) = ∑ i k ( x i ) − ( n − k + 1 ) ∗ p + n − k \sum_i^k(x_i - p + 1) = \sum_i^k(x_i) - (n - k + 1) * p + n - k i∑k(xi−p+1)=i∑k(xi)−(n−k+1)∗p+n−k
对这两个式子进行观察,发现每次加一其实就是n,之后前面得p - xi 和 xi - p其实就是前后缀跟p操作一系列操作的结果。
∑ i n ( ∣ x k − x i ∣ + 1 ) = k ∗ x k − ∑ i k ( x i ) + ∑ k n ( x i ) − ( n − i + 1 ) ∗ x k + n \sum_i^n(|x_k - x_i| + 1) = k * x_k - \sum_i^k(x_i) + \sum_k^n(x_i) - (n - i + 1) * x_k + n i∑n(∣xk−xi∣+1)=k∗xk−i∑k(xi)+k∑n(xi)−(n−i+1)∗xk+n
进而转换为:排序后对第k个,k * xk - pre[k],suf[k] - (n - k + 1) * xk,n的相加结果。
代码(记得LL):
void solve() {int n; cin>>n;vector<PII> a(n + 21);for(int i = 1; i <= n ;++i) {int t; cin>>t;a[i] = {t,i};}sort(a.begin() + 1, a.begin() + n + 1);vector<int> pre(n + 21), suf(n + 21);for(int i = 1; i <= n; ++i) {pre[i] = pre[i-1] + a[i].vf;}for(int i = n; i >= 1; --i) {suf[i] = suf[i+1] + a[i].vf;}vector<int> ans(n + 21);for(int i = 1; i <= n; ++i) {int x = a[i].vf;int pr = i * x - pre[i] + n;int sf = suf[i] - (n - i + 1) * x;ans[a[i].vs] = pr + sf;}for(int i = 1; i <= n; ++i) cout<<ans[i]<<" \n"[i == n];
}
C. Pull Your Luck
Problem - 1804C - Codeforces
题意:

思路:当等于2n时:
f ( 2 n ) = 2 n ( 2 n + 1 ) 2 = n ( 2 n + 1 ) f(2n) = \frac{2n(2n + 1)}{2} = n(2n + 1) f(2n)=22n(2n+1)=n(2n+1)
此时,(x + f(2n)) %n == x进行循环,因此进行枚举即可。
_ = int(input())
for __ in range(_):n,x,p = list(map(int, input().split(" ")))ok = Falsefor i in range(1,min(2 * n, p) + 1):k = i * (i + 1) // 2if((k + x) % n == 0):ok = Truebreakprint("Yes" if ok else "No")
CF1804C Pull Your Luck - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
F. Range Update Point Query
Problem - 1791F - Codeforces

解法一:线段树
区间修改用暴力,如果区间内都是小于10的表示这个区间不用再进行操作,可以知道这个每个位置的操作最多2、3次就不再进行操作。
#include <iostream>
#include <vector>
#include <string>
#include <cstring>
#include <set>
#include <map>
#include <queue>
#include <ctime>
#include <random>
#include <sstream>
#include <numeric>
#include <stdio.h>
#include <functional>
#include <bitset>
#include <algorithm>
using namespace std;#define Multiple_groups_of_examples
#define IOS std::cout.tie(0);std::cin.tie(0)->sync_with_stdio(false);
#define dbgnb(a) std::cout << #a << " = " << a << '\n';
#define dbgtt cout<<" !!!test!!! "<<endl;
#define rep(i,x,n) for(int i = x; i <= n; i++)#define all(x) (x).begin(),(x).end()
#define pb push_back
#define vf first
#define vs secondtypedef long long LL;
typedef pair<int,int> PII;const int INF = 0x3f3f3f3f;
const int N = 2e5 + 21;int calc(int x) {int tmp = 0; while(x) {tmp += x % 10; x /= 10; } return tmp;
}
int w[N],n,m; // 注意 w[N] 开LL ( https://www.luogu.com.cn/problem/P2357
struct SegTree {int l,r,val,tag;
}tr[N << 2];
// 左子树
inline int ls(int p) {return p<<1; }
// 右子树
inline int rs(int p) {return p<<1|1; }
// 向上更新
void pushup(int u) {tr[u].tag = tr[ls(u)].tag & tr[rs(u)].tag;
}// 建树
void build(int u, int l, int r) {if(l == r) {tr[u] = {l,r,w[l], w[l] < 10};}else {tr[u] = {l,r}; // 容易忘int mid = l + r >> 1;build(ls(u), l, mid), build(rs(u), mid + 1, r);pushup(u);}
}
// 修改
void modify(int u, int l, int r) {if(tr[u].l >= l && tr[u].r <= r && tr[u].tag) {return ;}if(tr[u].l == tr[u].r) {tr[u].val = calc(tr[u].val);tr[u].tag = tr[u].val < 10;return ;}int mid = tr[u].l + tr[u].r >> 1;if(l <= mid) modify(ls(u), l, r);if(r > mid) modify(rs(u), l, r);pushup(u);
}
// 查询
LL query(int u, int l, int r) {if(tr[u].l >= l && tr[u].r <= r) return tr[u].val;int mid = tr[u].l + tr[u].r >> 1;if(l <= mid) return query(ls(u), l,r);return query(rs(u), l, r);
}
void solve() {cin>>n>>m;for(int i = 1; i <= n; ++i) cin>>w[i];build(1, 1, n);while(m--) {int op,l,r; cin>>op;if(op == 1) {cin>>l>>r;modify(1,l,r);} else {cin>>l;cout<<query(1,l,l)<<endl;}}
}
int main()
{#ifdef Multiple_groups_of_examplesint T; cin>>T;while(T--)#endifsolve();return 0;
}
void inpfile() {#define mytest#ifdef mytestfreopen("ANSWER.txt", "w",stdout);#endif
}
解法二
其实可能就是解法一的简化版。因为每个位置最多操作2次就不再进行操作了,只需要维护一个还需要进行操作的一个元素下标,每次区间操作对这个还要操作的元素下标进行查找,复杂度线段树差不多。
注意:对set用lower_bound函数时一定要用set自带的,s.lower_bound(l),而不是lower_bound(all(s), l),这题亲测会TLE3(
void solve() {int n,q; cin>>n>>q;vector<int> a(n + 1);set<int> s;for(int i = 1; i <= n; ++i) {cin>>a[i];if(a[i] >= 10) s.insert(i);}auto calc = [&](int x) -> int {int tmp = 0;while(x) {tmp += x % 10;x /= 10;}return tmp;};while(q--) {int op,l,r;cin>>op;if(op == 1) {cin>>l>>r;auto t = s.lower_bound(l);while(t != s.end() && *t <= r) {l = *t;a[l] = calc(a[l]);if(a[l] < 10) {s.erase(l);}t = s.lower_bound(l+1);}} else {cin>>l;cout<<a[l]<<endl;}}
}
相关文章:

cf 解题报告 01
E. Power of Points Problem - 1857E - Codeforces 题意: 给你 n n n 个点,其整数坐标为 x 1 , … x n x_1,\dots x_n x1,…xn,它们位于一条数线上。 对于某个整数 s s s,我们构建线段[ s , x 1 s,x_1 s,x1], [ s , x…...
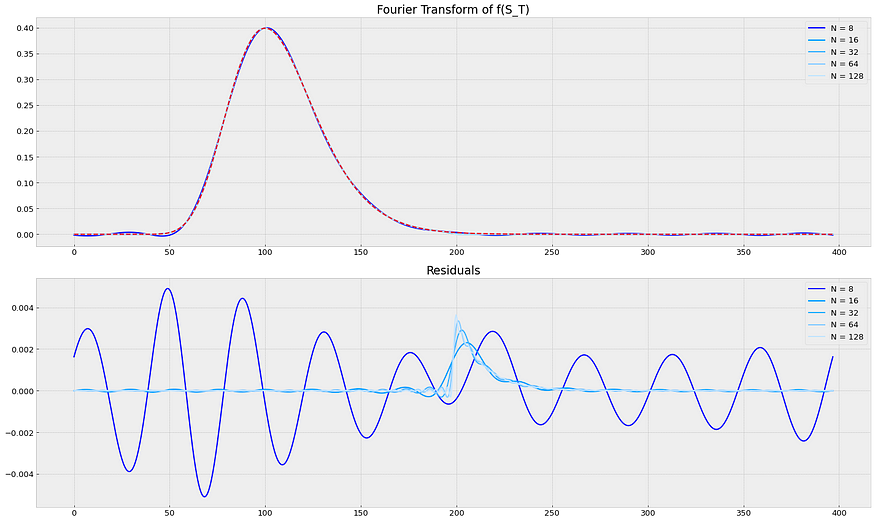
傅里叶系列 P1 的定价选项
如果您想了解更多信息,请查看第 2 部分和第 3 部分。 一、说明 这是第一篇文章,我将帮助您获得如何使用这个新的强大工具来解决金融中的半分析问题并取代您的蒙特卡洛方法的直觉。 我们都知道并喜欢蒙特卡洛数字积分方法,但是如果我告诉你你可…...

第二十届北京消防展即将开启,汉威科技即将精彩亮相
10月10日~13日,第二十届中国国际消防设备技术交流展览会,将在北京市顺义区中国国际展览中心新馆隆重举行。该展会由中国消防协会举办,是世界三大消防品牌展会之一,本届主题为“助力产业发展,服务消防救援”。届时将有4…...

mongodb、mysql、redis 区别
MongoDB、MySQL 和 Redis 是三种不同的数据库管理系统,它们在数据存储、访问模型和使用场景方面有一些显著的区别。 1. 数据存储模型: MongoDB:MongoDB 是一种文档数据库,它使用 BSON(Binary JSON)格式来存储数据。数据以文档的形式组织,每个文档可以有不同的字段,文档…...
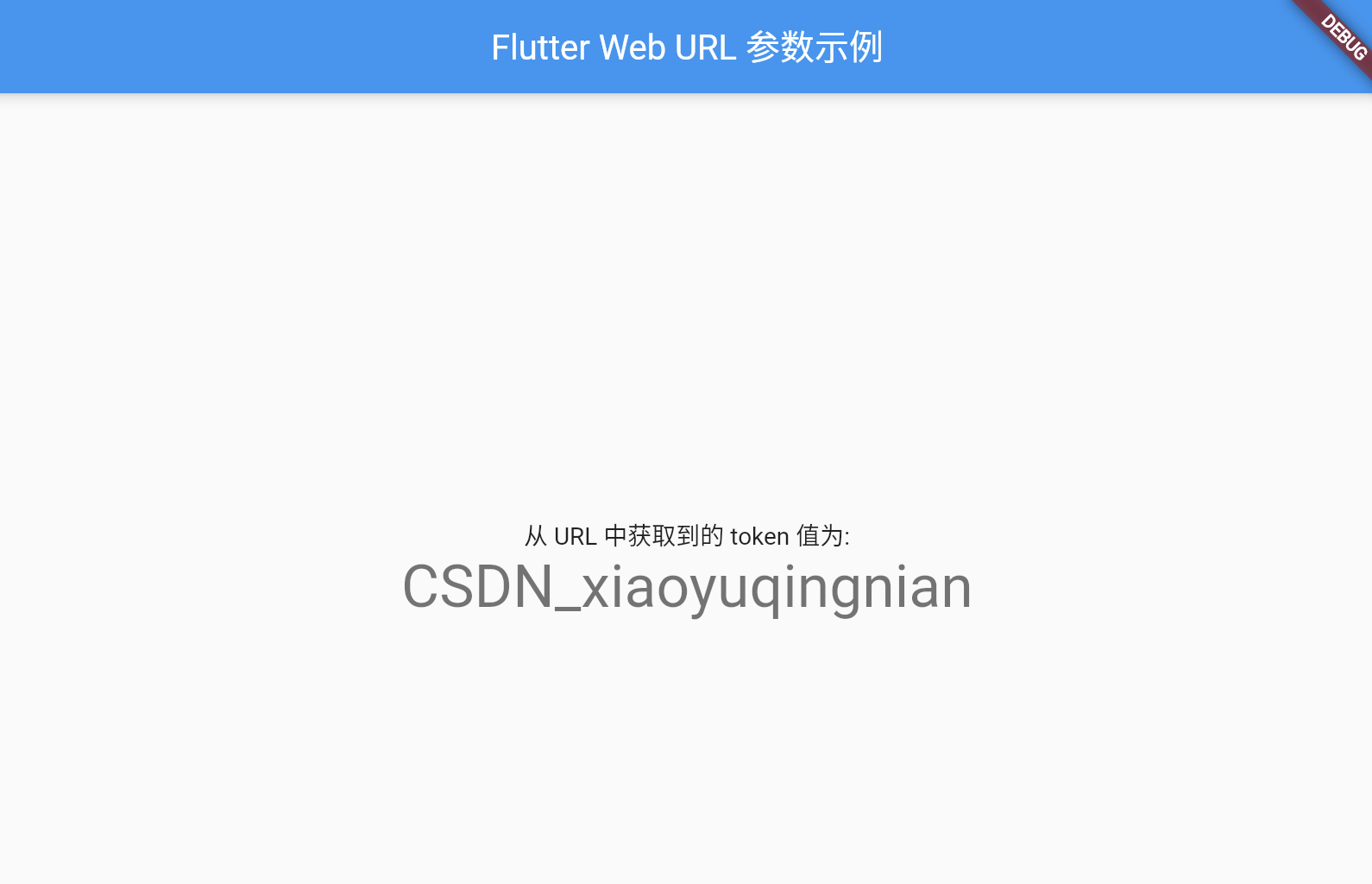
【Flutter】Flutter Web 开发 如何从 URL 中获取参数值
【Flutter】Flutter Web 开发 如何从 URL 中获取参数值 文章目录 一、前言二、Flutter Web 中的 URL 处理三、如何从 URL 中获取参数四、实际业务中的用法五、完整示例六、总结 一、前言 大家好!我是小雨青年,今天我想和大家分享一下在 Flutter Web 开发…...

【Java 进阶篇】JDBC Statement:执行 SQL 语句的重要接口
在Java应用程序中,与数据库进行交互是一项常见的任务。为了执行数据库操作,我们需要使用JDBC(Java Database Connectivity)来建立与数据库的连接并执行SQL语句。Statement接口是JDBC中的一个重要接口,它用于执行SQL语句…...

Python与数据分析--Pandas操作进阶
目录 1.文件读取方式 1.1.绝对路径读取文件 1.2.相对路径读取文件 2.列表数据操作 2.1.列索引指定 2.2.代码数据对齐 3.创建新CSV文件 4.缺失值处理 4.1.缺失值创建 4.2.缺失值检索 4.3.缺失值查询 4.3.1.isnull()函数判断 4.3.2.notnull()函数判断 4.3.3.any()函数…...

国庆小练习
一、二、三 一、 创建一个双向链表, 将26个英文字母通过头插的方式插入到链表中 通过尾删的方式将数据读取出来并删除。main.c #include <my_head.h> #include "dblink.h"int main(int argc, const char *argv[]) {dblink *h create_head();for…...

springboot单体项目如何拆分成微服务
要将一个Spring Boot单体项目拆分成微服务,可以按照以下步骤进行操作: 识别业务域:首先,需要对单体项目进行业务域的划分。将项目中的功能按照业务领域进行分类,每个业务领域可以成为一个独立的微服务。 定义服务接口…...

解决recovery页面反转的问题
1.前言 在android 10.0的系统rom定制化开发工作中,在系统中recoverv的页面也是相关重要的一部分,在系统recovery ta升级等功能,都是需要recoverv功能的,在某些产品定制化中 在recovery的时候,发现居然旋转了180度&…...
)
如何使用nuScenes数据集格式的单帧数据推理(以DETR3D为例)
【请尊重原创!转载和引用文章内容务必注明出处!未经许可上传到某文库或其他收费阅读/下载网站赚钱的必追究责任!】 无论是mmdetection3D还是OpenPCDet都只有使用数据集(使用哪个数据集由配置文件里指定)训练和测试的代码,没有使用…...
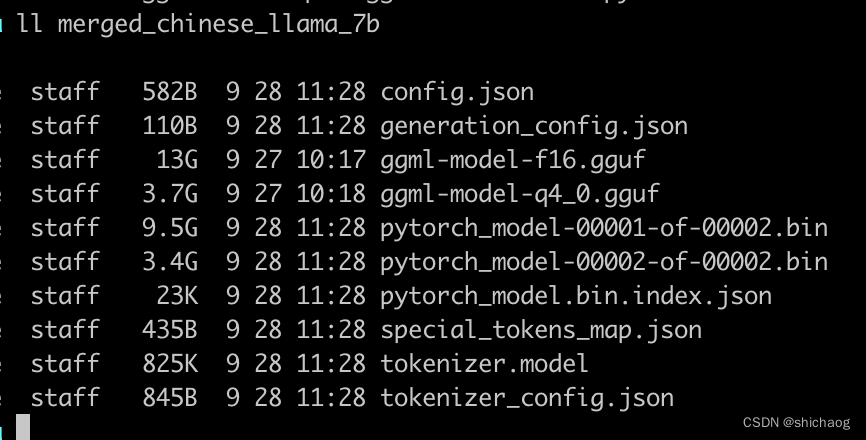
大语言模型之十三 LLama2中文推理
在《大语言模型之十二 SentencePiece扩充LLama2中文词汇》一文中已经扩充好了中文词汇表,接下来就是使用整理的中文语料对模型进行预训练了。这里先跳过预训练环节。先试用已经训练好的模型,看看如何推理。 合并模型 这一步骤会合并LoRA权重࿰…...

iOS AVAudioSession 详解
iOS AVAudioSession 详解 - 简书 默认没有options,category 7种即可满足条件 - (BOOL)setCategory:(AVAudioSessionCategory)category error:(NSError **)outError API_AVAILABLE(ios(3.0), watchos(2.0), tvos(9.0)) API_UNAVAILABLE(macos); 有optionsÿ…...
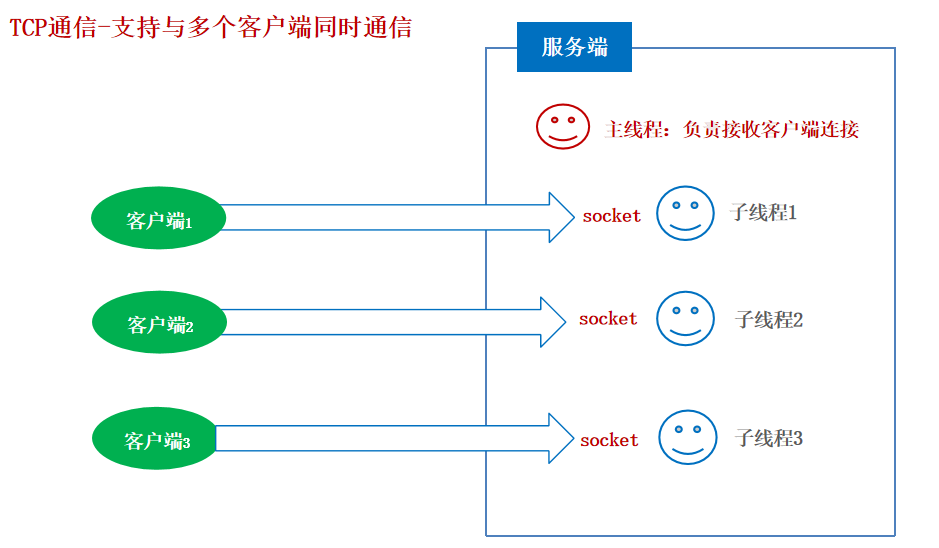
26-网络通信
网络通信 什么是网络编程? 可以让设备中的程序与网络上其他设备中的程序进行数据交互(实现网络通信的)。 java.net.包下提供了网络编程的解决方案! 基本的通信架构有2种形式:CS架构( Client客户端/Server服…...

嵌入式Linux应用开发-基础知识-第十九章驱动程序基石③
嵌入式Linux应用开发-基础知识-第十九章驱动程序基石③ 第十九章 驱动程序基石③19.5 定时器19.5.1 内核函数19.5.2 定时器时间单位19.5.3 使用定时器处理按键抖动19.5.4 现场编程、上机19.5.5 深入研究:定时器的内部机制19.5.6 深入研究:找到系统滴答 1…...
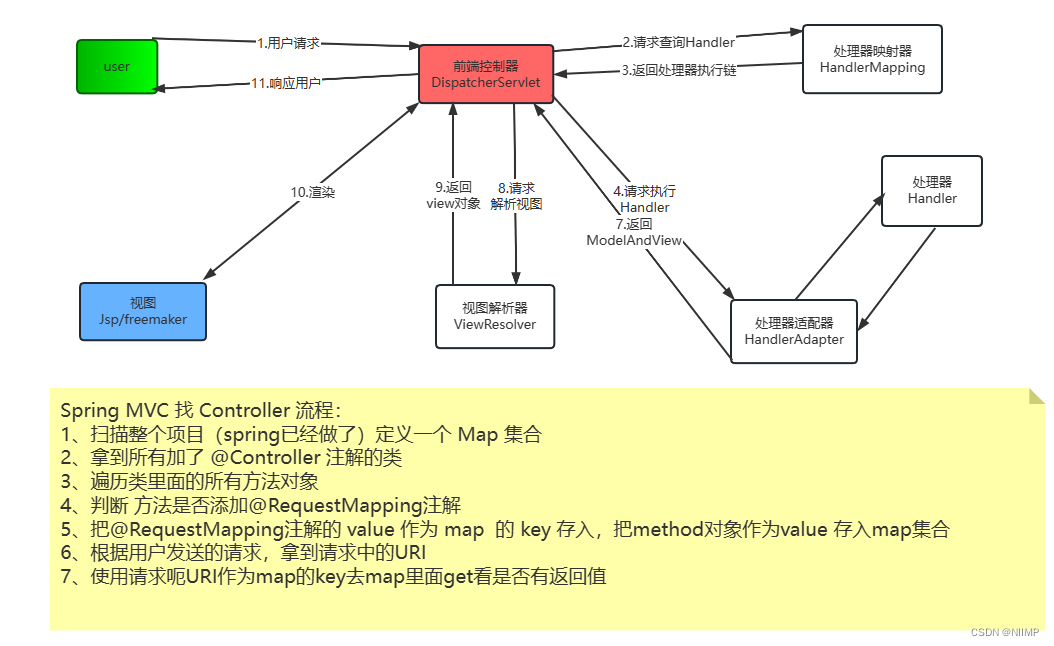
一文拿捏SpringMVC的调用流程
SpringMVC的调用流程 1.核心元素: DispatcherServlet(前端控制器)HandlerMapping(处理器映射器)HandlerAdapter(处理器适配器) ---> Handler(处理器)ViewResolver(视图解析器 )---> view(视图) 2.调用流程 用户发送请求到前端控制器前端控制器接收用户请求…...

一文详解 JDK1.8 的 Lambda、Stream、LocalDateTime
Lambda Lambda介绍 Lambda 表达式(lambda expression)是一个匿名函数,Lambda表达式基于数学中的λ演算得名,直接对应于其中的lambda抽象(lambda abstraction),是一个匿名函数,即没有函数名的函数。 Lambda表达式的结构 一个 Lamb…...

WebSocket实战之二协议分析
一、前言 上一篇 WebSocket实战之一 讲了WebSocket一个极简例子和基础的API的介绍,这一篇来分析一下WebSocket的协议,学习网络协议最好的方式就是抓包分析一下什么就都明白了。 二、WebSocket协议 本想盗一张网络图,后来想想不太好&#x…...
)
LeetCode //C - 208. Implement Trie (Prefix Tree)
208. Implement Trie (Prefix Tree) A trie (pronounced as “try”) or prefix tree is a tree data structure used to efficiently store and retrieve keys in a dataset of strings. There are various applications of this data structure, such as autocomplete and s…...
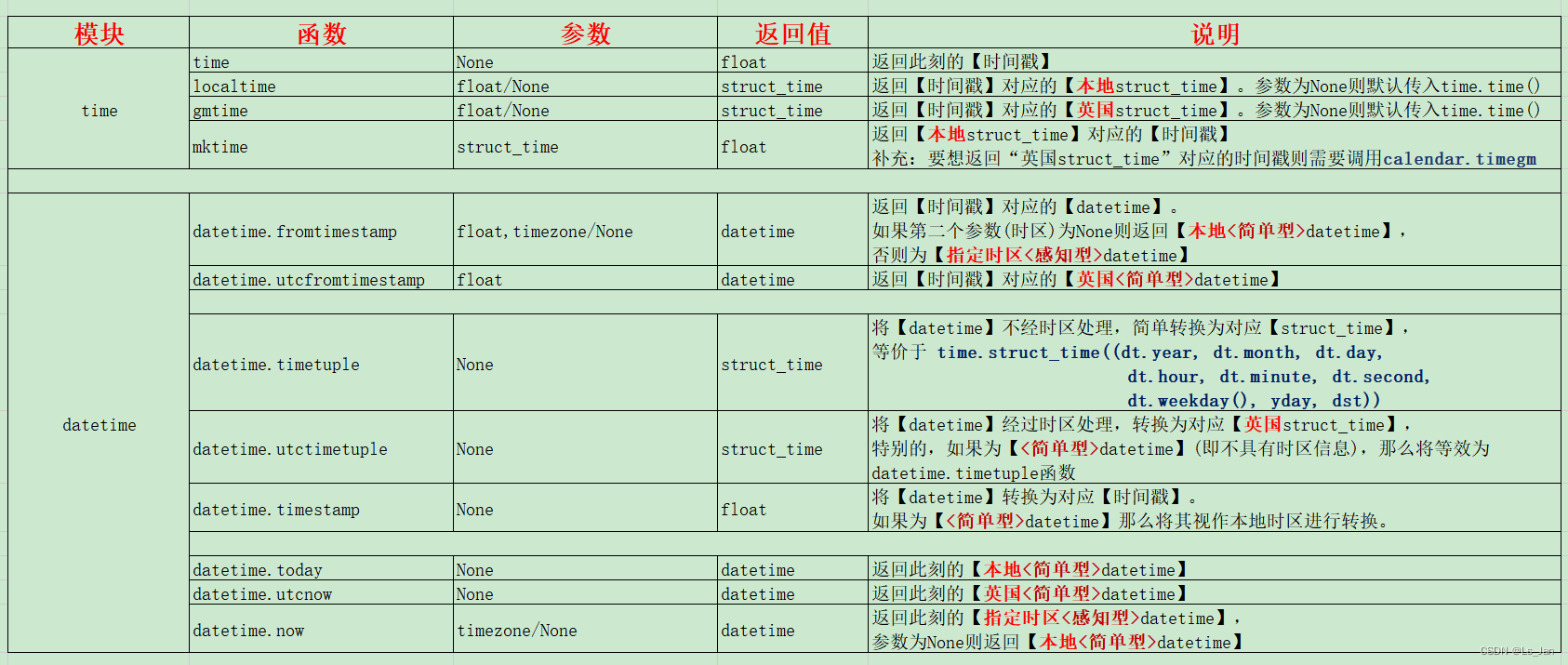
【Python】time模块和datetime模块的部分函数说明
时间戳与日期 在说到这俩模块之前,首先先明确几个概念: 时间戳是个很单纯的东西,没有“时区”一说,因为时间戳本质上是经过的时间。日常生活中接触到的“日期”、“某点某时某分”准确的说是时间点,都是有时区概念的…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
