常用求解器安装
1 建模语言pyomo
Pyomo是一个Python建模语言,用于数学优化建模。它可以与不同的求解器(如Gurobi,CPLEX,GLPK,SCIP等)集成使用,以求解各种数学优化问题。可以使用Pyomo建立数学优化模型,并将其发送到求解器来求解。要使用SCIP求解器,您需要安装SCIP软件包并将其配置为Pyomo的求解器之一。然后,您可以在Pyomo中指定SCIP作为您的求解器,并使用Pyomo接口将模型发送到SCIP以求解。
另外,Pyomo可以使用启发式算法来求解优化问题。Pyomo提供了一个插件pyomo.contrib.hybrid,它允许用户将Pyomo模型与任何启发式算法集成。您可以使用以下步骤在Pyomo中调用启发式算法:
(1)安装所需的启发式算法库,例如Particle Swarm Optimization(PSO),Simulated Annealing(SA)或Tabu Search(TS)。
(2)在Pyomo模型中定义目标函数和约束条件。
(3)使用pyomo.contrib.hybrid插件将Pyomo模型转换为适合启发式算法求解的问题。
(4)使用所选的启发式算法库来求解转换后的问题。
pyomo教程:
- https://jckantor.github.io/ND-Pyomo-Cookbook/notebooks/04.01-Introduction_to_Disjunctive_Programming.html
2 求解器安装
cplex安装
商用求解器
进入https://www.ibm.com/cn-zh/products/ilog-cplex-optimization-studio?utm_content=SRCWW&p1=Search&p4=43700074800244505&p5=2&gclid=CMa2nZ7KooEDFXNDwgUd1t0KIg&gclsrc=ds 下载试用版
https://blog.csdn.net/weixin_46034036/article/details/126813229?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169443599016800211562125%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=169443599016800211562125&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2alltop_click~default-2-126813229-null-null.142v93control&utm_term=cplex%20python&spm=1018.2226.3001.4187
- cplex22.1.1
打开anaconda cmd
conda create -n cplexEnv python=3.9.16
activate cplexEnv
D:
cd D:\Program Files\IBM\ILOG\CPLEX_Studio_Community2211\python
python setup.py install
这里直接安装在了base环境(python3.9),安装后,测试一下
from docplex.mp.model import Model
m = Model(name='single variable')
x = m.continuous_var(name="x", lb=0)
c1 = m.add_constraint(x >= 2, ctname="const1")
m.set_objective("min", 3*x)
m.print_information()
m.solve()
m.print_solution()
gurobi安装
商用求解器
reference:https://blog.csdn.net/weixin_41596280/article/details/89112302
-
打开https://www.gurobi.com/downloads/,注册账号后,下载Gurobi Optimizer
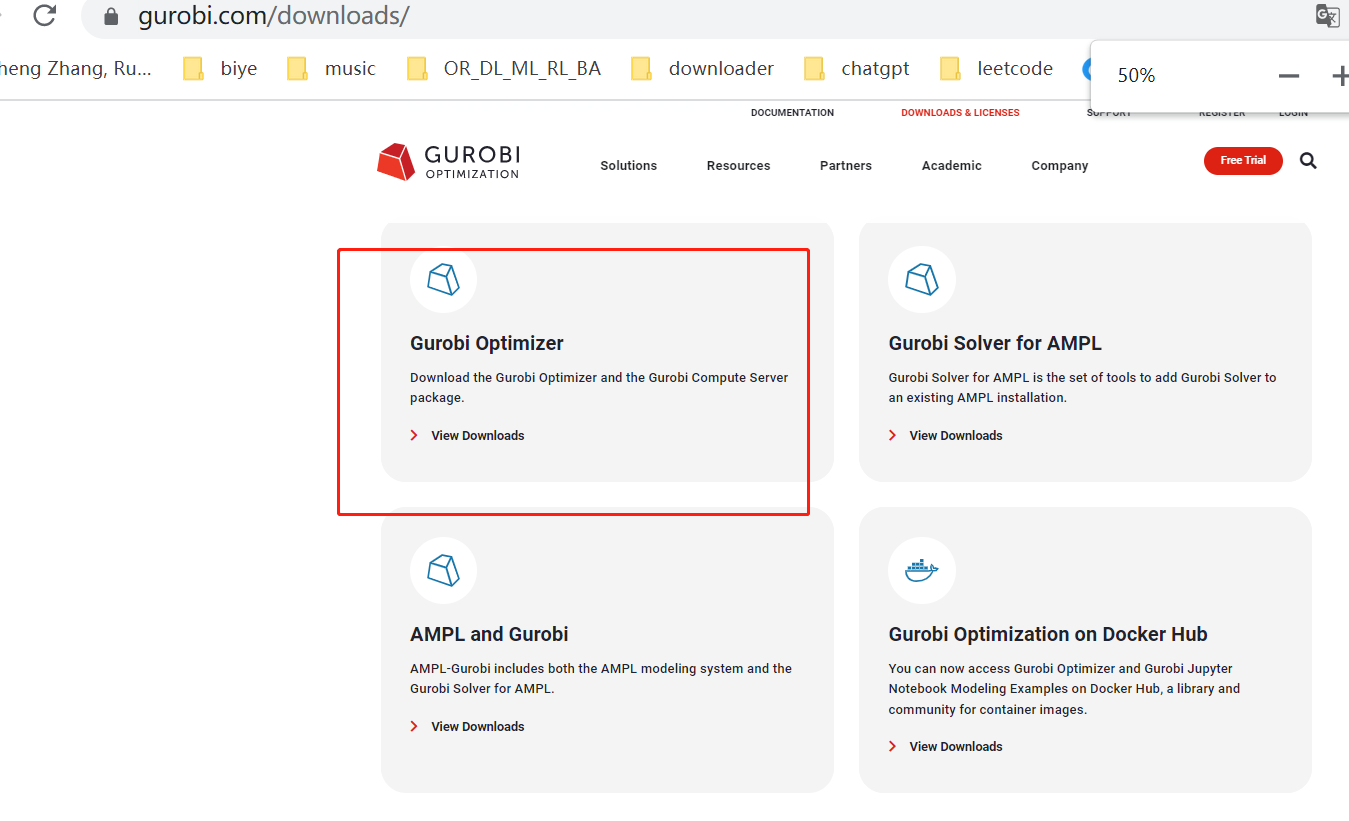
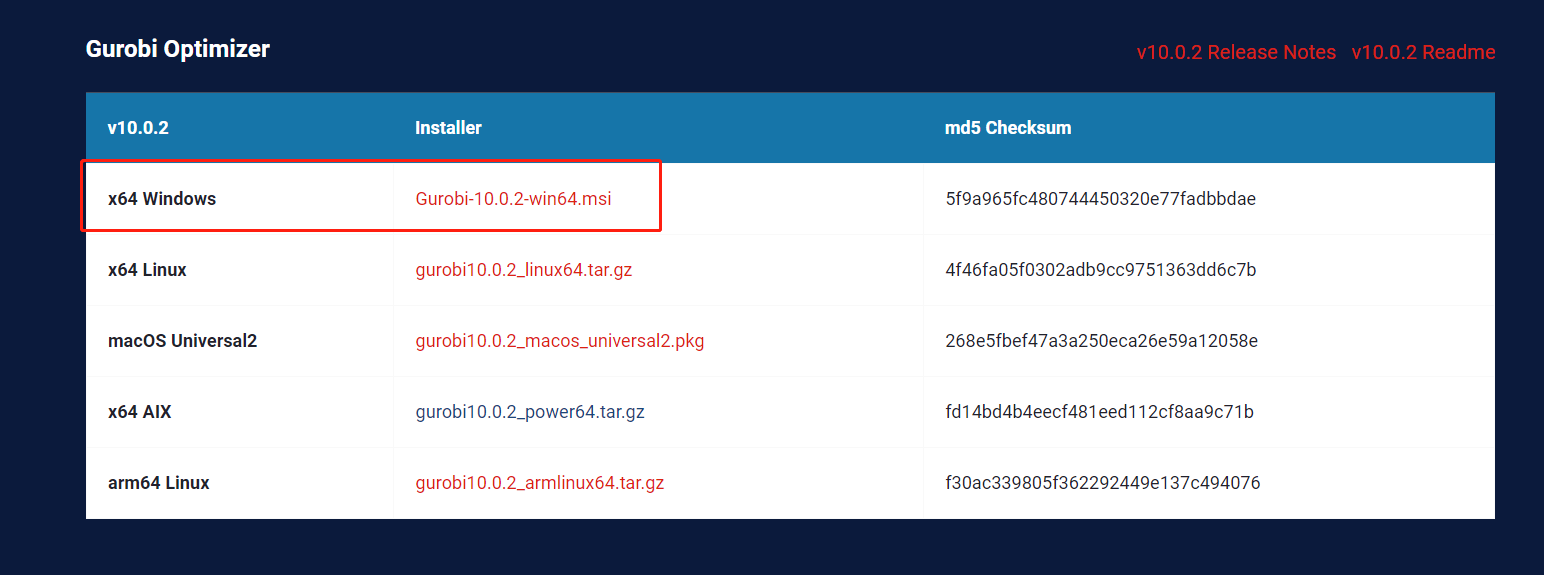
-
下载64位msi,然后安装
-
注册Gurobi 获取注册码 学术的是免费的,由于申请时会识别ip地址,所以需要连接校园网。免ip申请方式:
如果您是学生,需要申请学术许可,请去 http://www.gurobi.cn/NewsView1.Asp?id=4 网站按照步骤提示,提交资料申请一个免IP 验证学术许可。
如果您是企业人士,需要申请商业试用许可,或者商业资料,请去 http://www.gurobi.cn/NewsView1.Asp?id=9 , 填写表格后从公司邮箱发给我们。
-
python安装Gurobi
打开anaconda cmd
conda create -n gurobiEnv python=3.9.16 activate gurobiEnv D: cd D:\gurobi1002\win64 python setup.py install
glpk安装
reference:https://pyomo.readthedocs.io/en/stable/installation.html
conda install -c conda-forge ipopt glpk
SCIP安装
reference:
https://mp.weixin.qq.com/s/d92ds2wryk0T1lb2uPu_PA
http://www.taodudu.cc/news/show-3777585.html?action=onClick
https://github.com/scipopt/PySCIPOpt/blob/master/INSTALL.md
-
打开https://scipopt.org/index.php#download,下载64位exe,然后一路往下点,改存储文件夹。
-
还需要下载visual C++的一个东西:https://learn.microsoft.com/en-US/cpp/windows/latest-supported-vc-redist?view=msvc-170#visual-studio-2013-vc-120
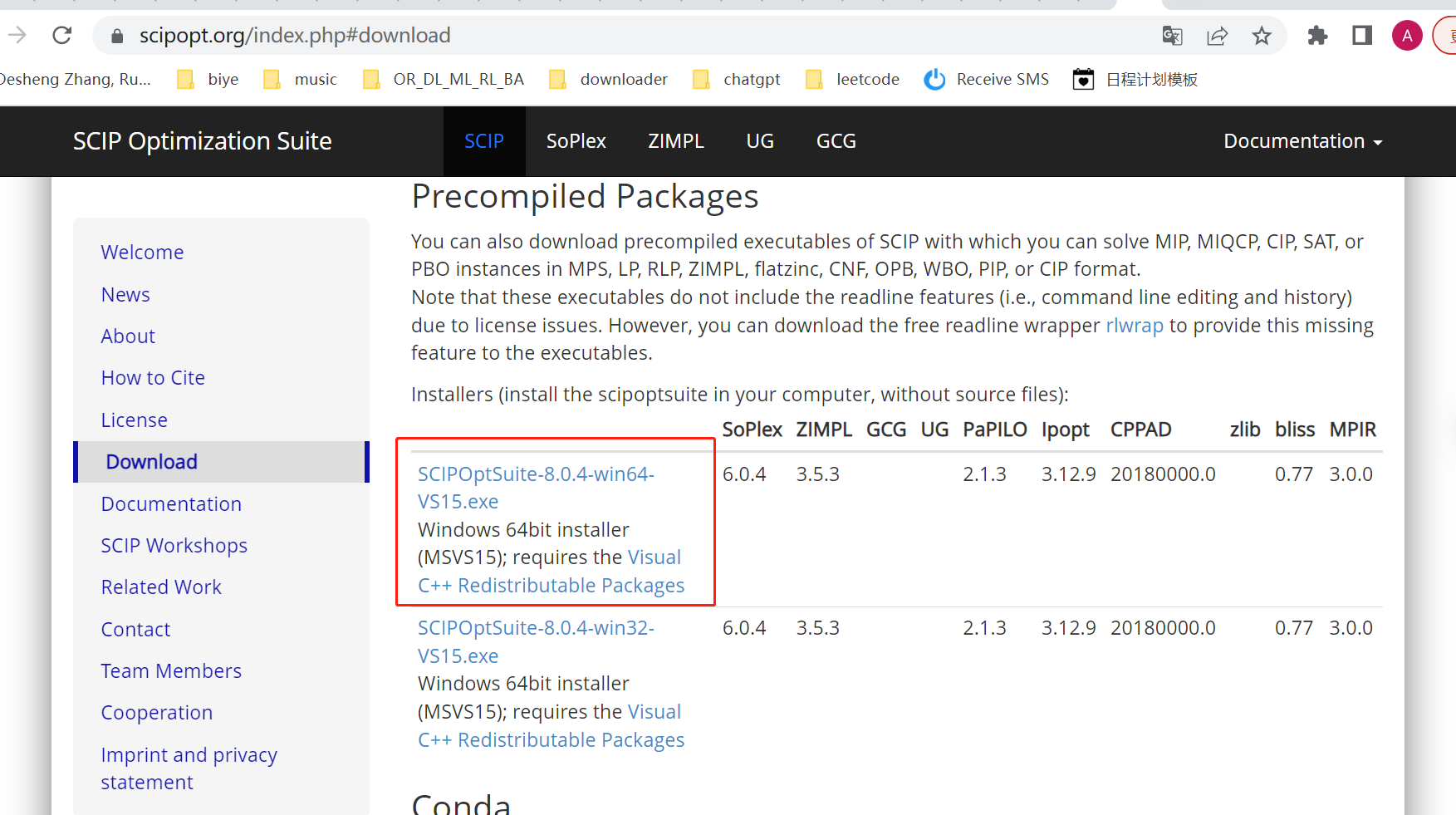
-
新建系统变量:
- 变量名:SCIPOPTDIR
- 变量值:D:\Program Files\SCIPOptSuite 8.0.4
-
在系统变量的path中添加“%SCIPOPTDIR%\bin”,“%SCIPOPTDIR%\include”,“%SCIPOPTDIR%\lib”
-
在用户变量的path中添加“%SCIPOPTDIR%\bin”
-
看看自己添加成功否,
win+R打开cmd,输入scip.exe,如果可以打开,说明变量成功添加到路径里了。 -
activate opt python -m pip install pyscipopt==4.3.0 # python-V=3.9.16
SCIP小例子
min x + y 2 x − y 2 ≥ 0 x ≥ 0 , y ∈ Z \min x+y\\ 2x - y^2\geq 0\\ x\geq 0,y\in \Z minx+y2x−y2≥0x≥0,y∈Z
import pyscipopt
from pyscipopt import Model"""
min x+y
2x - y^2 >=0
x>=0, y\in \Z"""if __name__ == '__main__':model = Model("Example")x = model.addVar("x")y = model.addVar("y", vtype="INTEGER")model.setObjective(x + y)model.addCons(2*x - y*y >= 0)model.optimize()sol = model.getBestSol()print("x: {}".format(sol[x]))print("y: {}".format(sol[y]))
相关文章:

常用求解器安装
1 建模语言pyomo Pyomo是一个Python建模语言,用于数学优化建模。它可以与不同的求解器(如Gurobi,CPLEX,GLPK,SCIP等)集成使用,以求解各种数学优化问题。可以使用Pyomo建立数学优化模型…...
)
第三章:最新版零基础学习 PYTHON 教程(第一节 - Python 运算符)
在Python编程中,运算符一般用于对值和变量进行操作。这些是用于逻辑和算术运算的标准符号。在本文中,我们将研究不同类型的Python 运算符。 运算符:这些是特殊符号。例如- + 、 * 、 / 等。操作数:它是应用运算符的值。目录 Python 中的运算符类型 Python 中的算术运算符…...
细粒度特征提取和定位用于目标检测:PPCNN
1、简介 近年来,深度卷积神经网络在计算机视觉上取得了优异的性能。深度卷积神经网络以精确地分类目标信息而闻名,并采用了简单的卷积体系结构来降低图层的复杂性。基于深度卷积神经网络概念设计的VGG网络。VGGNet在对大规模图像进行分类方面取得了巨大…...

【STM32单片机】数学自动出题器设计
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用STM32F103C8T6单片机控制器,使用按键、IIC OLED模块等。 主要功能: 系统运行后,OLED液晶显示出题器开机界面,默认结果范围为100,可按…...
C语言之动态内存管理篇(1)
目录 为什么存在动态内存分配 动态内存函数的介绍 malloc free calloc realloc 常见的动态内存错误 今天收假了,抓紧时间写几篇博客。我又来赶进度了。今天我们来讲解动态内存管理。🆗🆗 为什么存在动态内存分配 假设我们去实现一个…...
React18入门(第二篇)——React18+Ts项目配置husky、eslint、pretttier、commitLint
前言 我的项目版本如下: React: V18.2.0Node.js: V16.14.0TypeScript:最新版工具: VsCode 本文将采用图文详解的方式,手把手带你快速完成在React项目中配置husky、prettier、commitLint,实现编码规范的统…...
【VINS】苹果手机采集单目相机+IMU数据离线运行VINS-Mono
0.准备工作 开个新坑,之前用Android手机做过离线采集数据的实验,这次用IPhone来测试! 1.虚拟机配置Mac OS 下载一个Mac OS 的ios镜像,打开虚拟机按照跟Ubuntu差不多的方式安装,但是发现没有Mac OS的入口。 因为VMwa…...
数据结构 2.1 单链表
1.单链表 线性表:1.有限的序列 2.序列中的每一个元素都有唯一的前驱和后继,除了开头和结尾的两个节点。 顺序表:分配一块连续的内存去存放这些元素,eg、数组 链表:内存是不连续的,元素会各自被分配一块内…...
[Machine Learning]pytorch手搓一个神经网络模型
因为之前虽然写过一点点关于pytorch的东西,但是用的还是他太少了。 这次从头开始,尝试着搓出一个神经网络模型 (因为没有什么训练数据,所以最后的训练部分使用可能不太好跑起来的代码作为演示,如果有需要自己连上数据…...
KdMapper扩展实现之Dell(pcdsrvc_x64.pkms)
1.背景 KdMapper是一个利用intel的驱动漏洞可以无痕的加载未经签名的驱动,本文是利用其它漏洞(参考《【转载】利用签名驱动漏洞加载未签名驱动》)做相应的修改以实现类似功能。需要大家对KdMapper的代码有一定了解。 2.驱动信息 驱动名称pcds…...

python和go相互调用的两种方法
前言 Python 和 Go 语言是两种不同的编程语言,它们分别有自己的优势和适用场景。在一些项目中,由于团队内已有的技术栈或者某一部分业务的需求,可能需要 Python 和 Go 相互调用,以此来提升效率和性能。 性能优势 Go 通常比 Python 更高效&…...

c# 分部视图笔记
Html.Partial("**", 1) public ActionResult **(int page) { ViewBag.page page; return PartialView("**"); }...

Vue3最佳实践 第七章 TypeScript 中
Vue组件中TypeScript 在Vue组件中,我们可以使用TypeScript进行各种类型的设置,包括props、Reactive和ref等。下面,让我们详细地探讨一下这些设置。 设置描述设置props在Vue中,props本身就具有类型设定的功能。但如果你希望使用Ty…...
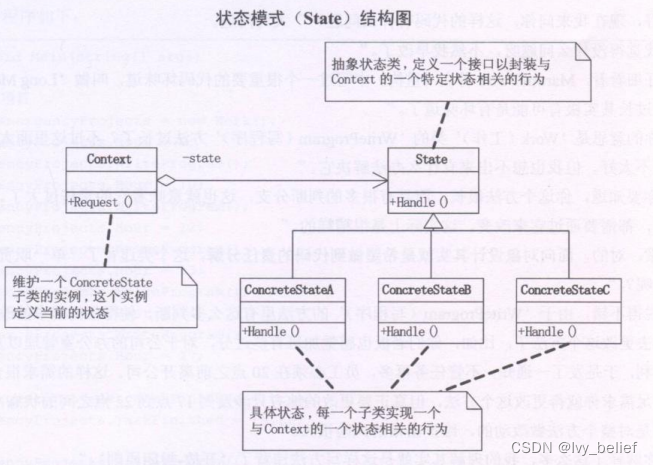
(三)行为模式:8、状态模式(State Pattern)(C++示例)
目录 1、状态模式(State Pattern)含义 2、状态模式的UML图学习 3、状态模式的应用场景 4、状态模式的优缺点 (1)优点 (2)缺点 5、C实现状态模式的实例 1、状态模式(State Pattern&#x…...
)
nginx的配置文件概述及简单demo(二)
默认配置文件 当安装完nginx后,它的目录下通常有默认的配置文件 #user nobody; worker_processes 1;#error_log logs/error.log; #error_log logs/error.log notice; #error_log logs/error.log info;#pid logs/nginx.pid;events {worker_connection…...
Apollo Planning2.0决策规划算法代码详细解析 (2): vscode gdb单步调试环境搭建
前言: apollo planning2.0 在新版本中在降低学习和二次开发成本上进行了一些重要的优化,重要的优化有接口优化、task插件化、配置参数改造等。 GNU symbolic debugger,简称「GDB 调试器」,是 Linux 平台下最常用的一款程序调试器。GDB 编译器通常以 gdb 命令的形式在终端…...

flex 布局:元素/文字靠右
前言 略 使用flex的justify-content属性控制元素的摆放位置 靠右 <view class"more">展开更多<text class"iconfont20231007 icon-zhankai"></text></view>.more {display: flex;flex-direction: row;color: #636363;justify-co…...
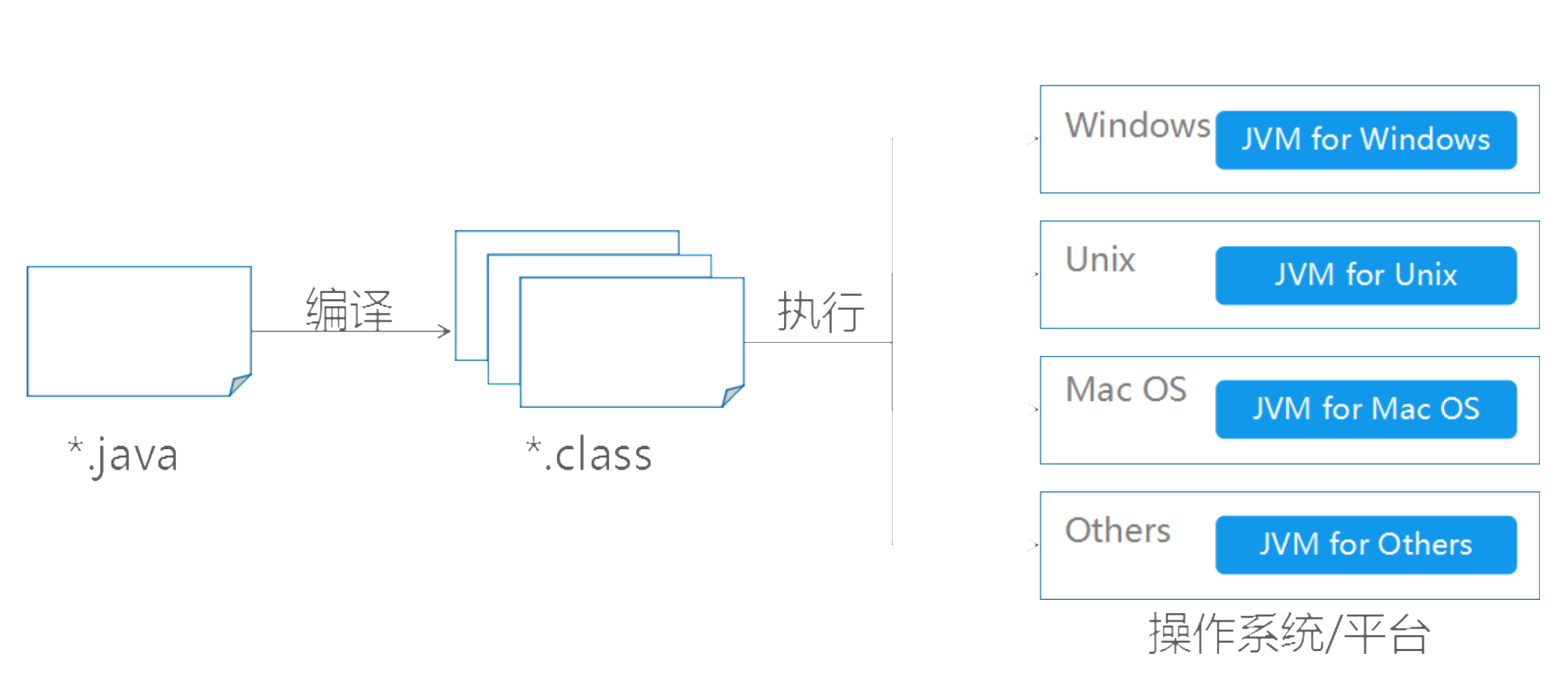
java基础-第1章-走进java世界
一、计算机基础知识 常用的DOS命令 二、计算机语言介绍 三、Java语言概述 四、Java环境的搭建 JDK安装图解 环境变量的配置 配置环境变量意义 配置环境变量步骤 五、第一个Java程序 编写Java源程序 编译Java源文件 运行Java程序 六、Java语言运行机制 核心机制—Java虚拟机 核…...

jvm 堆内存 栈内存 大小设置
4种方式配置不同作用域的jvm的堆栈内存。 1、Eclise 中设置jvm内存: 改动eclipse的配置文件,对全部project都起作用 改动eclipse根文件夹下的eclipse.ini文件 -vmargs //虚拟机设置 -Xms40m //初始内存 -Xmx256m //最大内存 -Xmn16m //最小内存 -XX:PermSize=128M //非堆内…...
免杀对抗-反沙盒+反调试
反VT-沙盒检测-Go&Python 介绍: 近年来,各类恶意软件层出不穷,反病毒软件也更新了各种检测方案以提高检率。 其中比较有效的方案是动态沙箱检测技术,即通过在沙箱中运行程序并观察程序行为来判断程序是否为恶意程序。简单来说…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
