变压器绕组断股往往导致直流电阻不平衡率超标
变压器绕组断股往往导致直流电阻不平衡率超标, 例如, 某电厂 SFPSL—12000/220 型主变压器, 色谱分析结果发现总烃含量急剧增长, 测直流电阻, 其结果是高、 低压侧与制造厂及历年的数值相比较无异常, 但中压侧的直流电阻A、 B 相偏大, 如表 7 所示的换算值。
在分析 A、 B 相直流电阻增大的原因时, 考虑到变压器在运行中曾 遭受过两次严重短路电流冲击, 所以怀疑是绕组断股, 经解体检查发现, 故障点部位在 A 相引 线在套管的根部附近, 并且 A 相套管根部与套管均压帽焊在一起, 引 线烧断的面积为 42. 3mm² , 占总截面积的 10%。 由于故障点在 A 相引 线, 所以与该引 线相连接的 B 相直流电阻也增大。为消除由于断股引 起的直流电阻不平衡率超标,
宜采取的措施有:
(1) 变压器受到短路电流冲击后, 应及时测量其直流电阻, 及时发现断股故障, 及时检修。
(2) 利用 色谱分析结果进行综合分析判断, 经验证明,这是一种有效方法。
相关文章:

变压器绕组断股往往导致直流电阻不平衡率超标
变压器绕组断股往往导致直流电阻不平衡率超标, 例如, 某电厂 SFPSL—12000/220 型主变压器, 色谱分析结果发现总烃含量急剧增长, 测直流电阻, 其结果是高、 低压侧与制造厂及历年的数值相比较无异常, 但中压…...
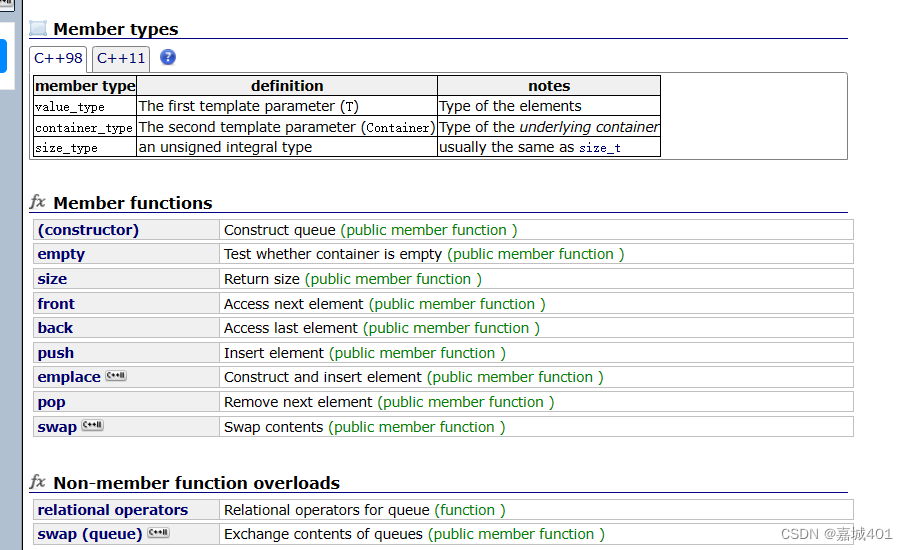
stack和queque
1.stack 1.1定义 T 是容器内的数据类型; Container是数据类型的容器适配器 vector和list和stack的区别 1.2 stack的功能 注意这里没有迭代器;原因stack是先进后出的规律;这就规定该容器不可以随机访问; 2. queue...

信息学 学习/复习 抽签器(附源码)
问你一个问题,你考试前怎么复习呀? 效果图 以下是源代码,可自行修改 [C] #include<bits/stdc.h> #include<windows.h> using namespace std; vector<string>item; int main(void) {item.push_back("Manacher"…...
基于LADRC自抗扰控制的VSG三相逆变器预同步并网控制策略(Simulink仿真实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

[0xGame 2023] week1
整理一下,昨天该第二周了。今天应该9点结束提交,等我写完就到了。 PWN 找不到且不对劲的flag 第1题是个nc测试,但也不完全是,因为flag在隐含目录里 高端的syscall 程序使用了危险函数,并且没有canary阻止࿰…...

Matlab矩阵——矩阵行列互换
问题:如何将 1*n 的矩阵转换为指定 M*N 的矩阵,或者将 M*N 的矩阵转换为 1*n 的矩阵? 处理方法:使用 reshape 函数进行矩阵的行列互换 分两种情况如下: 一、将 1*n 的矩阵转换为指定 M*N 的矩阵 假如有4个坐标值&a…...

OpenMesh 网格面片随机赋色
文章目录 一、简介二、实现代码三、实现效果一、简介 OpenMesh中的赋色方式与Easy3D很是类似,它统一有一个属性数组来进行管理,我们在进行赋色等操作时,必须要首先添加该属性才能进行使用,这里也进行记录一下(法向量等特征也是类似的操作)。 二、实现代码 #define _USE_…...
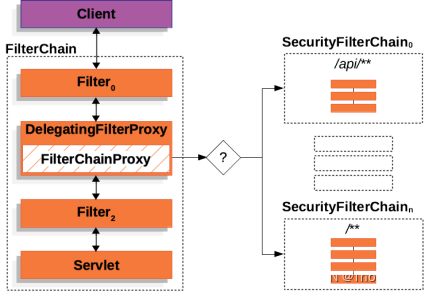
SpringSecurity源码学习一:过滤器执行原理
目录 1. web过滤器Filter1.1 filter核心类1.2 GenericFilterBean1.3 DelegatingFilterProxy1.3.1 原理1.3.2 DelegatingFilterProxy源码 2. FilterChainProxy源码学习2.1 源码2.1.1 doFilterInternal方法源码2.1.1.1 getFilters()方法源码2.1.1.2 VirtualFilterChain方法源码 3…...
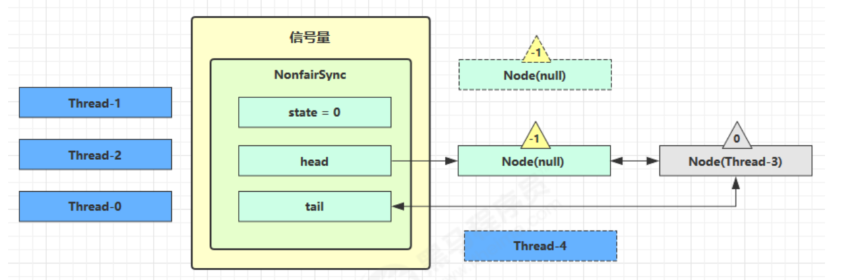
8.2 JUC - 4.Semaphore
目录 一、是什么?二、简单使用三、semaphore应用四、Semaphore原理 一、是什么? Semaphore:信号量,用来限制能同时访问共享资源的线程上限 二、简单使用 public class TestSemaphore {public static void main(String[] args) …...

前端try和catch
为什么要使用try catch 使用try...catch语句是为了处理和管理可能会在程序运行过程中发生的异常或错误情况。以下是一些使用try...catch的主要原因: 错误处理:在开发过程中,无法避免地会出现各种错误,如网络请求失败、数据解析错误…...

Unity可视化Shader工具ASE介绍——2、ASE的Shader创建和输入输出
大家好,我是阿赵,这里继续介绍Unity可视化写Shader的ASE插件的用法。上一篇介绍了ASE的安装和编辑器界面分布,这一篇主要是通过一个简单的例子介绍shader的创建和输入输出。 一、ASE的Shader创建 这里先选择Surface类型的Shader,…...
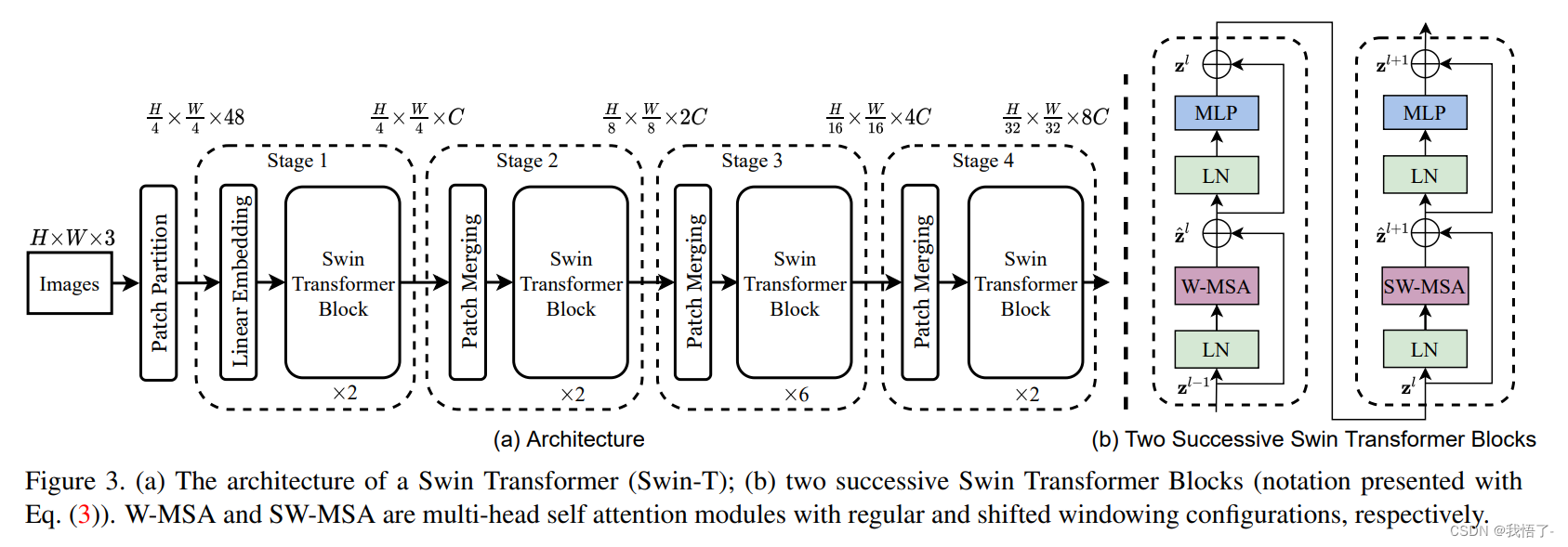
目标检测算法改进系列之Backbone替换为Swin Transformer
Swin Transformer简介 《Swin Transformer: Hierarchical Vision Transformer using Shifted Windows》作为2021 ICCV最佳论文,屠榜了各大CV任务,性能优于DeiT、ViT和EfficientNet等主干网络,已经替代经典的CNN架构,成为了计算机…...
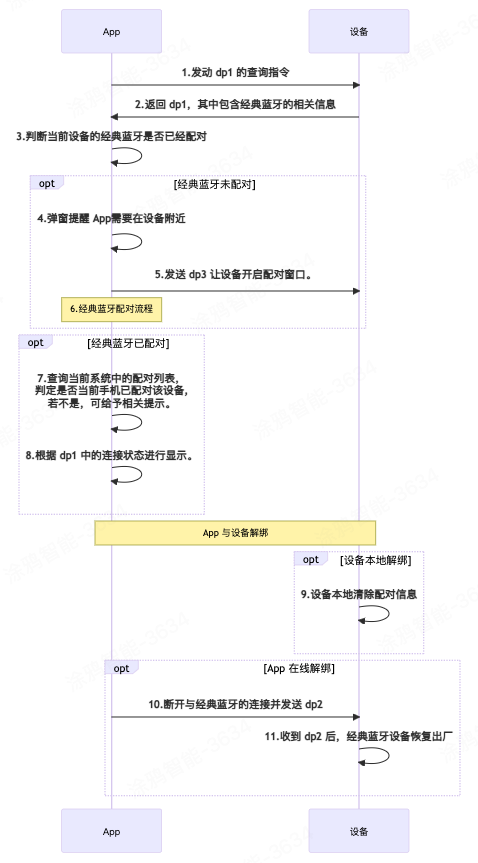
【技术干货】如何通过 DP 实现支持经典蓝牙的联网单品设备与 App 配对
经典蓝牙模块(Classic Bluetooth)主要用于呼叫和音频传输,所以经典蓝牙最主要的特点就是功耗大,传输数据量大。蓝牙耳机、蓝牙音箱等场景大多采用经典蓝牙,因为蓝牙是为传输声音而设计的,是短距离音频传输的…...

【Unity Build-In管线的SurfaceShader剖析_PBS光照函数】
Unity Build-In管线的SurfaceShader剖析 在Unity Build-In 管线(Universal Render Pipeline)新建一个Standard Surface Shader文件里的代码如下:选中"MyPBR.Shader",在Inspector面板,打开"Show generat…...

thinkphp5实现ajax图片上传,压缩保存到服务器
<div class"warp"><input type"file" id"file" accept"image/*" onchange"upimg(this)" /></div> <img src"" /> <script>//上传图片方法function upimg(obj){var fileData obj.…...
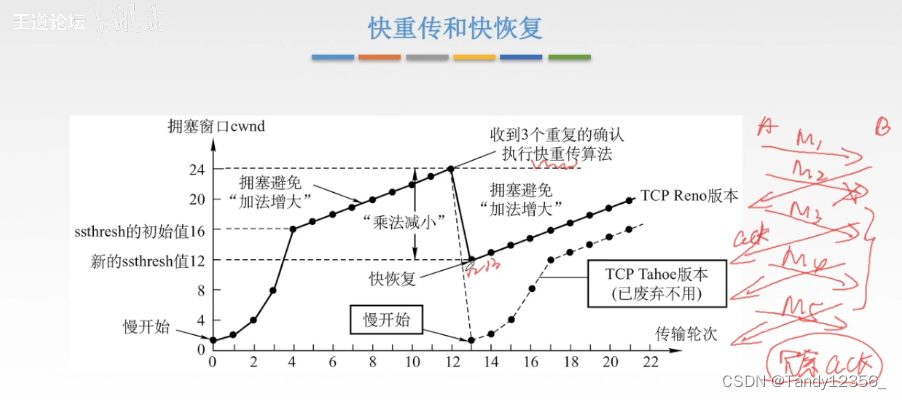
王道考研计算机网络——传输层
一、传输层概述 复用:发送方不同的应用进程都可以使用同一个传输层的协议来传送数据 分用:接收方的传输层在去除报文段的首部之后能把数据交给正确的应用进程 熟知端口号就是知名端口号0-1023 客户端使用的端口号是动态变化的,不是唯一确定…...
)
08 集群参数配置(下)
Kafka Broker不需要太大的堆内存? Kafka Broker不需要太大的堆内存?应该把内存留给页缓存使用? kafka刷盘时宕机 kafka认为写入成功是指写入页缓存成功还是数据刷到磁盘成功算成功呢?还是上次刷盘宕机失败的问题,页…...
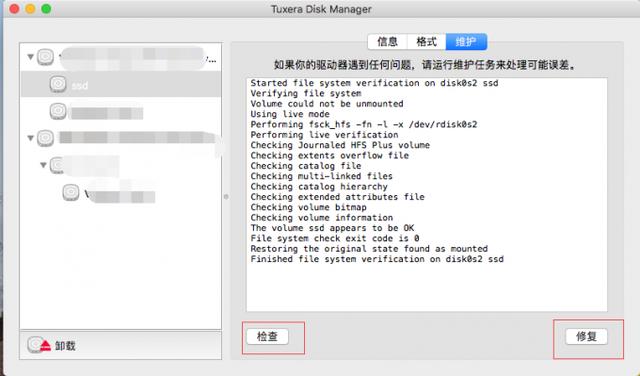
mac文件为什么不能拖进U盘?
对于Mac用户来说,可能会遭遇一些烦恼,比如在试图将文件从Mac电脑拖入U盘时,却发现文件无法成功传输。这无疑给用户带来了很大的不便。那么,mac文件为什么不能拖进U盘,看完这篇你就知道了。 一、U盘的读写权限问题 如果…...

RK3568的CAN驱动适配
目录 背景: 1.内核驱动模块配置 2.设备树配置 3.功能测试 4.bug修复 背景: 某个项目上使用RK3568的芯片,需要用到4路CAN接口进行通信,经过方案评审后决定使用RK3568自带的3路CAN外加一路spi转的CAN实现功能,在这个…...

Opengl之立方体贴图
简单来说,立方体贴图就是一个包含了6个2D纹理的纹理,每个2D纹理都组成了立方体的一个面:一个有纹理的立方体。你可能会奇怪,这样一个立方体有什么用途呢?为什么要把6张纹理合并到一张纹理中,而不是直接使用6个单独的纹理呢?立方体贴图有一个非常有用的特性,它可以通过一…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
