算法题:买卖股票的最佳时机含手续费(动态规划解法贪心解法-详解)
这道题有两种解法:动态规划 or 贪心算法。
贪心算法的提交结果要比动态规划好一些,总体上动态规划的解法更容易想到。(完整题目附在了最后)
1、动态规划解法
设置两个数,dp[0]表示遍历到股票prices[i]时手里没有股票情况下的纯利润(要么就是无操作,要么就是卖掉手里的股票,卖掉股票是要减去fee,两种操作之间选择利益最大的做法); dp[1]表示遍历到股票prices[i]时手里有股票情况下的纯利润(在“无操作”和“购入当前股票”两种做法之间选择利益最大的做法),那么遍历到股票prices[i+1]时,
dp = [max(dp[0], dp[1] + prices[i] - fee), max(dp[1], dp[0] - prices[i])]。
根据整体意思,dp初始化时为 [0, -prices[0]]。
# 动态规划解法
class Solution(object):def maxProfit(self, prices, fee):n = len(prices)dp = [0, -prices[0]]for i in range(1, n):dp = [max(dp[0], dp[1] + prices[i] - fee), max(dp[1], dp[0] - prices[i])]return max(dp)2、贪心解法
1)在连续递减的情况下买入价格最低时的股票,在不亏本的情况下如果连续递增则在最高点卖掉股票(因为要多考虑一个fee的费用,所以不亏本的前提要加上)。
2)代码有点弯弯绕在里面,就是在还没买入的时候我们把手续费fee加到当前股票价格price上面,遍历prices数组,判断各个相邻price+fee后的大小,在连续递减的情况下选择最低点的买入。
3)买入之后就要寻找最高点卖出,我们继续往后遍历,找到卖出能够有利润的第一支股票,设置一个“虚拟卖出”,由于后面的股票价格可能更高,所以这里不一定是当前这笔交易最后卖出的价格。如果后面的股票价格更高,则把价格差加入到profit里面,直到股票价格开始下降,当前交易才算完成,购入点为最低点,卖出点为有利润的情况下的最高点。
4)重复2)与3)中的买入卖出步骤,直到遍历完prices数组。
# 贪心解法
class Solution:def maxProfit(self, prices, fee):n = len(prices)profit = 0budget = prices[0] + feefor i in range(1, n):if prices[i] + fee < budget:budget = prices[i] + feeelif prices[i] > budget:profit += prices[i] - budgetbudget = prices[i]return profit3、完整题目:
714. 买卖股票的最佳时机含手续费
给定一个整数数组 prices,其中 prices[i]表示第 i 天的股票价格 ;整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意:这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费。
示例 1:
输入:prices = [1, 3, 2, 8, 4, 9], fee = 2 输出:8 解释:能够达到的最大利润: 在此处买入 prices[0] = 1 在此处卖出 prices[3] = 8 在此处买入 prices[4] = 4 在此处卖出 prices[5] = 9 总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8
示例 2:
输入:prices = [1,3,7,5,10,3], fee = 3 输出:6
提示:
1 <= prices.length <= 5 * 10^41 <= prices[i] < 5 * 10^40 <= fee < 5 * 10^4
相关文章:

算法题:买卖股票的最佳时机含手续费(动态规划解法贪心解法-详解)
这道题有两种解法:动态规划 or 贪心算法。 贪心算法的提交结果要比动态规划好一些,总体上动态规划的解法更容易想到。(完整题目附在了最后) 1、动态规划解法 设置两个数,dp[0]表示遍历到股票prices[i]时手里没有股…...

【gcc】RtpTransportControllerSend学习笔记 4:码率分配
本文是woder大神 的文章的学习笔记。 大神的webrtc源码分析(8)-拥塞控制(上)-码率预估 详尽而具体,堪称神作。 gcc保障带宽公平性,预估码率后要分配码率,实现qos效果: webrtc源码分析(9)-拥塞控制(下)-码率分配 是 woder 大神进一步给出的另一篇神作。 本文是对(https://w…...

「专题速递」AR协作、智能NPC、数字人的应用与未来
元宇宙是一个融合了虚拟现实、增强现实、人工智能和云计算等技术的综合概念。它旨在创造一个高度沉浸式的虚拟环境,允许用户在其中交互、创造和共享内容。在元宇宙中,人们可以建立虚拟身份、参与虚拟社交,并享受无限的虚拟体验。 作为互联网大…...

什么是基于意图的网络(IBN)
基于意图的网络是一种网络技术,它根据业务意图(来自网络管理员的服务请求)配置 IT 基础架构,无需任何人工干预,它不断提供关键的网络见解,并不断调整硬件配置以确保满足意图,它将网络从以设备为…...
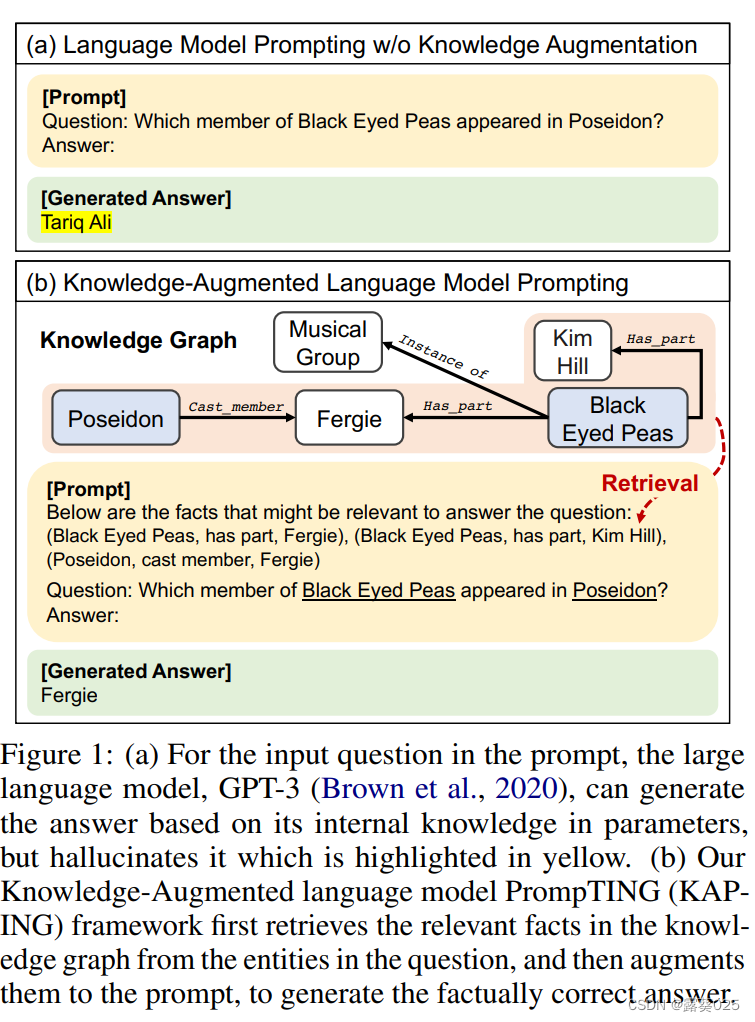
知识增强语言模型提示 零样本知识图谱问答10.8
知识增强语言模型提示 零样本知识图谱问答 摘要介绍相关工作方法零样本QA的LM提示知识增强的LM提示与知识问题相关的知识检索 摘要 大型语言模型(LLM)能够执行 零样本closed-book问答任务 ,依靠其在预训练期间存储在参数中的内部知识。然而&…...

虚拟现实项目笔记:SDK、Assimp、DirectX Sample Browser、X86和X64
文章目录 SDK是什么Assimp是什么DirectX Sample Browser是什么X86和X64生成解决方案和重新生成解决方案 SDK是什么 SDK是Software Development Kit的英文缩写,意思是软件开发包。 软件开发包中往往包含有多种辅助进行软件开发的内容,包括一些软件开发工…...
openwrt rm500u ncm方式拨号步骤记录
1.进入设备页面 用户名:root 2.创建接口 3.配置接口 国内APN 信息 中国移动APN:CMNET 中国联通APN:3GNET 中国电信APN:CTNET 4.防火墙配置 5.点击Save&Apply 6.配置完成后重启设备。重新进入设备页面,可以看…...

使用js代码将一个值为“1=增量,2=全量“的字符串转化为一个数组,数据格式为[{value:““,label:“‘‘}]
const str "1增量,2全量"; const arr str.split(",").map(item > {const [value, label] item.split("");return { value, label}; });...

图片调色盘
图片预览 配置安装 Color-Thief 安装包使用文档 yarn add colorthief -S // npm install colorthief --save代码 <template><div class"img-thief"><div class"container"><div class"thief-item" v-for"(item, in…...
一文读懂Base64
这几天在和第三方交互的时候,对方返回的数据是base64格式的数据,所以这两天又彻底捋了下Base64的来龙去脉。之前看过一篇文章说的非常好(再找到给加上链接),我在这不详细说明了,只说转换过程。 还是使用中…...

CCF CSP认证 历年题目自练 Day20
题目一 试题编号: 201903-1 试题名称: 小中大 时间限制: 1.0s 内存限制: 512.0MB 问题描述: 题目分析(个人理解) 常规题目,先看输入,第一行输入n表示有多少数字&am…...

【Overload游戏引擎分析】从视图投影矩阵提取视锥体及overload对视锥体的封装
overoad代码中包含一段有意思的代码,可以从视图投影矩阵逆推出摄像机的视锥体,本文来分析一下原理 一、平面的方程 视锥体是用平面来表示的,所以先看看平面的数学表达。 平面方程可以由其法线N(A, B, C)和一个点Q(x0,…...

vue全局事件总线是什么?有什么用?解决了什么问题,与pinia有什么区别?
全局事件总线快速入门 概念基本概念(是什么?)核心概念 核心特性和优势(有什么用?)解决了什么问题?主要优势是什么? 案例演示?传递数据-案例演示传递事件-案例演示 与pinia有什么区别?…...
【debian 12】:debian系统切换中文界面
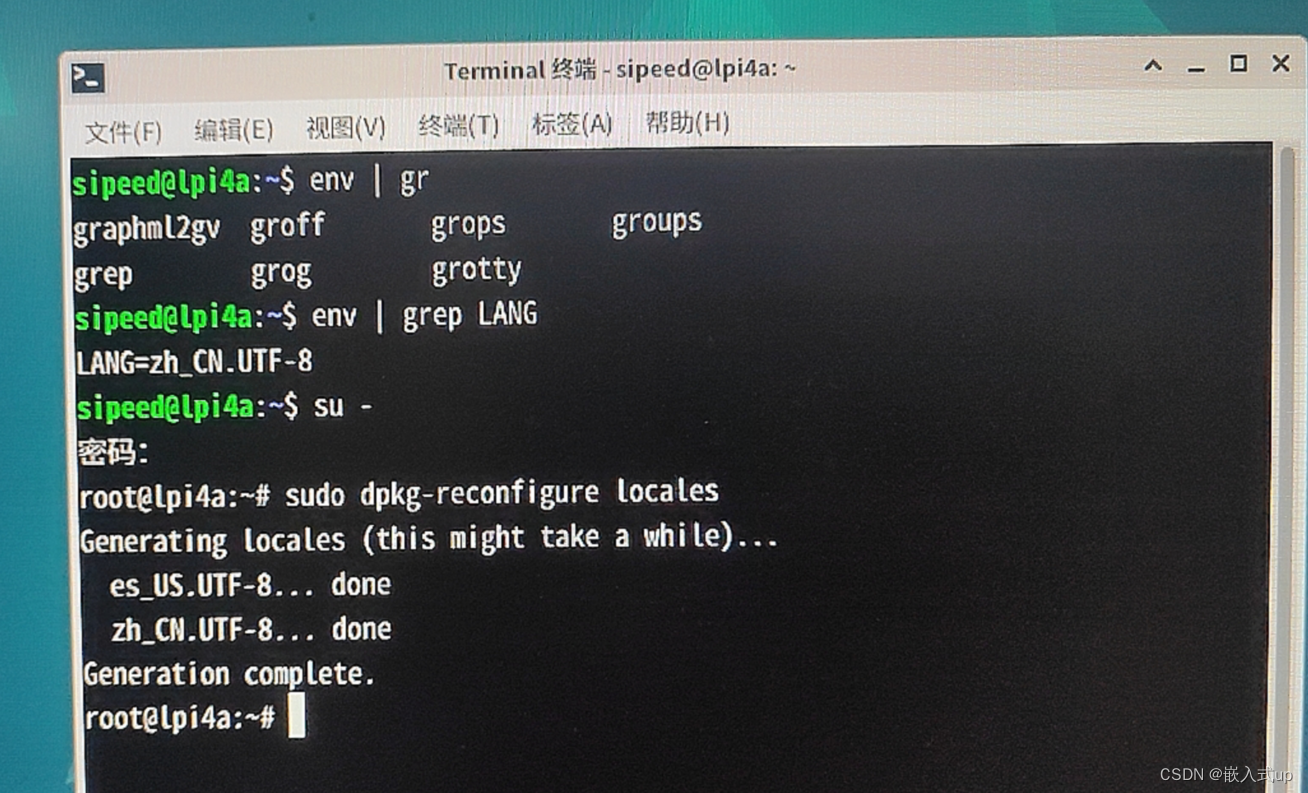
目录 目录 项目场景 基础参数 原因分析 解决方案 1.ctrlaltT 打开终端 2.查询当前语言环境(我的已经设置成了中文 zh_CN.UTF-8) 3.打开语言配置界面 4.最后一步:重启 不要放弃任何一个机会! 项目场景: 这两…...
)
es官方为我们提供的堆内存保护机制-熔断器( breaker )
总熔断器(相当于似乎总闸) 参数: indices.breaker.total.use_real_memory 默认值:true 在 elasticsearch.yml中配置。 参数: indices.breaker.total.limit 如果 indices.breaker.total.use_real_memory : true, in…...

靶场通关记录
OSCP系列靶场-Esay-CyberSploit1 总结 getwebshell → 源码注释发现用户名 → robots.txt发现base64密码 → SSH登录 提 权 思 路 → 内网信息收集 → 发现发行版本有点老 → 内核overlayfs提权 准备工作 启动VPN 获取攻击机IP > 192.168.45.220 启动靶机 获取目标机器I…...
全网最新最全的软件测试面试题
一、前言 与开发工程师相比,软件测试工程师前期可能不会太深,但涉及面还是很广的。 在一年左右的实习生或岗位的早期面试中,主要是问一些基本的问题。 涉及到的知识主要包括MySQL数据库的使用、Linux操作系统的使用、软件测试框架问题、测试…...
如何列出 Ubuntu 和 Debian 上已安装的软件包
当你安装了 Ubuntu 并想好好用一用。但在将来某个时候,你肯定会遇到忘记曾经安装了那些软件包。 这个是完全正常。没有人要求你把系统里所有已安装的软件包都记住。但是问题是,如何才能知道已经安装了哪些软件包?如何查看安装过的软件包呢&a…...

图论---最小生成树问题
在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树。解决最小生成树问题一般有两种算法:Kruskal算法和Prim算法。 Kruskal算法 原理:基本思想是从小到大加入边,是个贪心算法。我们将图中的每个边按…...

elementplus 时间范围选择器限制选择时间范围
<el-date-pickerv-model"form.time" type"daterange"range-separator"-"start-placeholder"开始时间"end-placeholder"结束":disabled-date"disabledDate"calendar-Change"calendarChange" />co…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...
