windows消息机制
windows开发比较简单,首先要理解的就是消息机制。
Windows消息机制是指Windows操作系统中的消息传递机制。在Windows中,应用程序通过消息进行通信和交互。消息是一种轻量级的通信方式,用于在不同的窗口、线程或进程之间传递信息。
在Windows消息机制中,消息由消息源发送到消息目标,消息目标可以是窗口、控件或线程。消息源可以是用户输入、系统事件或其他应用程序发送的消息。消息包含一个消息ID和一些附加的参数,用于描述事件或操作。
当消息发送到目标时,目标会将消息放入消息队列中。然后,消息循环(Message Loop)会从消息队列中取出消息,并将其分发给对应的窗口或控件进行处理。消息循环是一个无限循环,负责处理消息和事件,并将其传递给适当的消息处理函数(消息处理器)进行处理。
消息处理函数是应用程序开发者定义的回调函数,用于处理特定类型的消息。当消息循环将消息分发给窗口或控件时,会根据消息ID调用相应的消息处理函数进行处理。消息处理函数可以根据消息的类型和参数来执行相应的操作,例如更新界面、响应用户输入等。
通过消息机制,Windows提供了一种灵活的方式来处理用户交互、系统事件和应用程序之间的通信。它允许应用程序以异步的方式接收和处理消息,实现了窗口和控件的事件驱动编程模型。同时,消息机制也提供了一种安全的方式来跨线程或进程进行通信,避免了资源竞争和数据同步的问题。
总之,Windows消息机制是一种基于消息传递的通信机制,通过消息和消息处理函数实现应用程序之间的交互和通信。它是Windows应用程序开发中重要的基础机制之一。
相关文章:

windows消息机制
windows开发比较简单,首先要理解的就是消息机制。 Windows消息机制是指Windows操作系统中的消息传递机制。在Windows中,应用程序通过消息进行通信和交互。消息是一种轻量级的通信方式,用于在不同的窗口、线程或进程之间传递信息。 在Windows…...

整数划分——DP
用 j j j 个数表示 i i i 的方案数,考虑dp 转移考虑最小值是否为1 无限制 若为1,则转移到 f ( i 1 , j 1 ) f(i1, j1) f(i1,j1)不为1,则全部1,转移到 f ( i j , j ) f(ij, j) f(ij,j) 数之间不能重复 那么相当于每次整…...

Git切换用户常用命令
1、查看 查看用户名 : git config user.name查看密码: git config user.password查看邮箱: git config user.email查看配置信息(包含上面的信息): $ git config --list2、新增、切换 修改用户名 git…...

一般香港服务器带宽选多大够用?(带宽计算方法)
在海外IDC市场份额中,香港服务器依托自身优越的服务器资源条件,在各个行业中发挥的重要作用。但是,不同业务对网络带宽的要求各不相同,弄清楚如何计算带宽需求对于确保业务平稳运行至关重要,最好从一开始就使用正…...

vue中使用ali-oss上传文件到阿里云上
1.使用 npm 安装ali-oss npm install ali-oss --save2.写ali-oss.js // 引入ali-oss let OSS require(ali-oss) let client new OSS({region: oss-cn-xxx, // bucket所在的区域, 默认oss-cn-hangzhousecure: true, // secure: 配合region使用,如果指…...
计算时间的函数及其示例说明)
php实战案例记录(17)计算时间的函数及其示例说明
在PHP中,有许多函数可以用于计算和处理时间。以下是一些常用的计算时间的函数及其示例说明: time():获取当前时间的Unix时间戳。 $currentTimestamp time(); echo $currentTimestamp;date():将Unix时间戳格式化为指定的日期和时…...

基于Keil a51汇编 —— MPL 宏定义
MPL 宏 Ax51汇编程序支持的宏处理语言(MPL)是一种字符串替换工具,使您能够编写可修复的代码块(宏)并将其插入源文本中的一个或多个位置。 宏处理器查看源文件的方式与汇编程序不同。 对于汇编程序来说,源…...
——点击拍照到存入相册)
Android 13 骁龙相机点击拍照流程分析(二)——点击拍照到存入相册
一.前言 本篇是在Android 13 骁龙相机点击拍照流程分析(一)——点击拍照到更新到左下角缩略图文章的基础上进行延申的,前面的预览、点击拍照的过程参考第一篇:Android 13 骁龙相机点击拍照流程分析(一)——点击拍照到更新到左下角缩略图-CSDN博客 二.生成图片并保存 从第…...
)
常见算法-巴斯卡三角形(Pascal)
常见算法-巴斯卡三角形(Pascal) 1、说明 巴斯卡(Pascal)三角形基本上就是在解 nCr,因为三角形上的每一个数字各对应一个nCr,其中 n 为 row,而 r 为 column,如下: 0C0 1…...

AI:09-基于深度学习的图像场景分类
图像场景分类是计算机视觉领域的重要任务之一,它涉及将图像分为不同的场景类别,如城市街景、山脉风景、海滩等。本文将介绍基于深度学习的图像场景分类方法,并提供相应的代码实例,展示了深度学习在图像场景分类中的技术深度和应用前景。 图像场景分类是计算机视觉中的一项…...
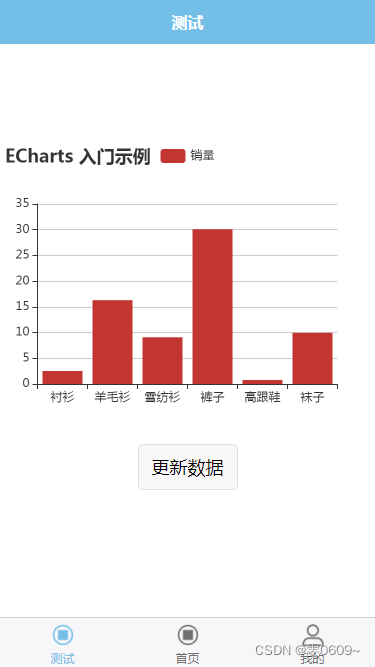
uni-app:引入echarts(使用renderjs)
效果 代码 <template><view click"echarts.onClick" :prop"option" :change:prop"echarts.updateEcharts" id"echarts" class"echarts"></view> </template><script>export default {data()…...
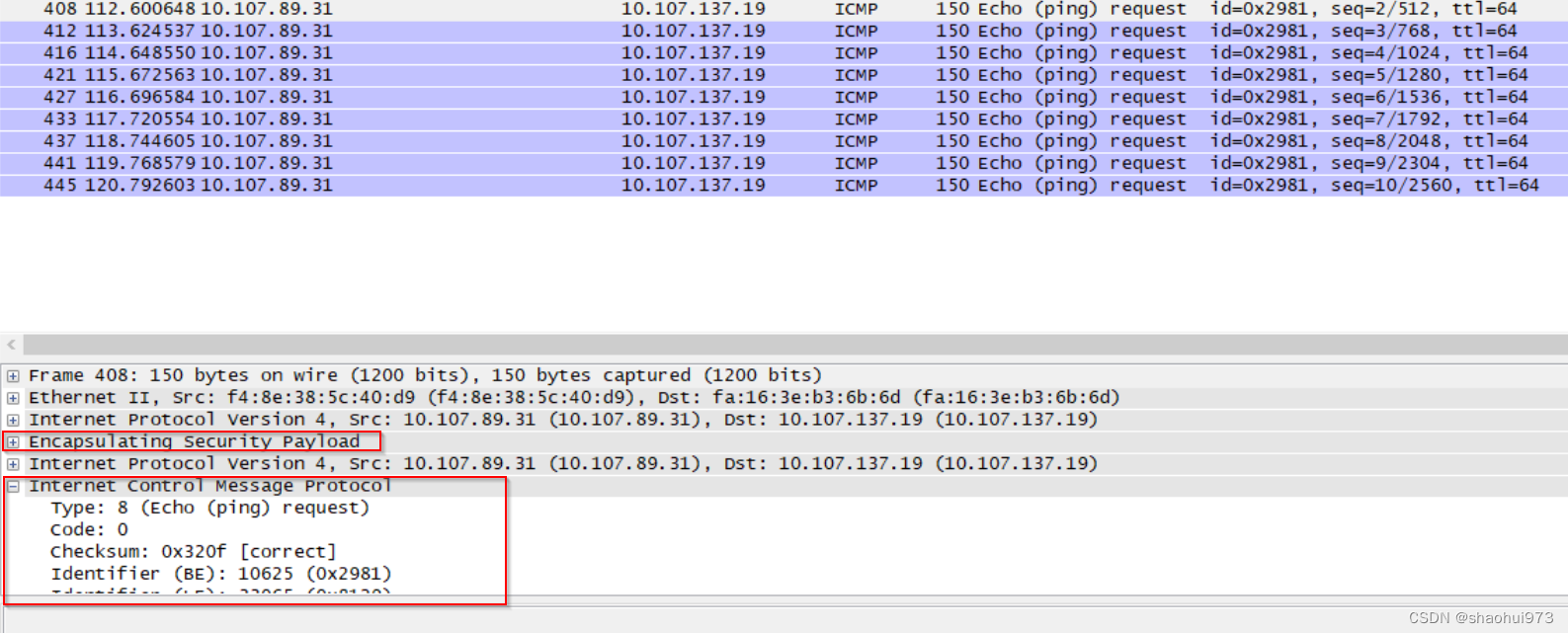
使用wireshark解析ipsec esp包
Ipsec esp包就是ipsec通过ike协议协商好后建立的通信隧道使用的加密包,该加密包里面就是用户的数据,比如通过的语音等。 那么如何将抓出来的esp包解析出来看呢? 获取相关的esp的key信息. 打开wireshark -> edit->preferences 找到pr…...

linux如何删除最近操作的日志
Linux系统下,不同的应用程序可能会生成不同的日志文件。如果你想要删除最近一段时间内的操作日志,可以使用一些命令来完成。 以下是一些常见的命令: dmesg:该命令用于显示内核环境下的运行信息和警告信息。如果你需要清空dmesg缓…...

android端MifareClassicTool
github地址 GitHub - ikarus23/MifareClassicTool: An Android NFC app for reading, writing, analyzing, etc. MIFARE Classic RFID tags. 开源项目 下载: https://www.icaria.de/mct/releases/ 功能 1、读取Mifare Classic卡片 2、编辑并保存卡片的数据 3、写入Mifare C…...
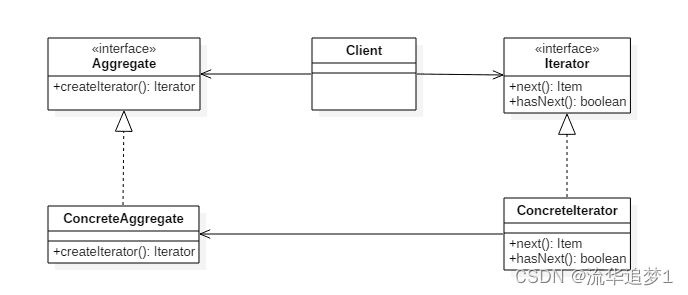
设计模式 - 迭代器模式
目录 一. 前言 二. 实现 三. 优缺点 一. 前言 迭代器模式是一种行为型设计模式,它提供了一种统一的方式来访问集合对象中的元素,而不暴露集合内部的表示方式。简单地说,就是将遍历集合的责任封装到一个单独的对象中,我们可以按…...
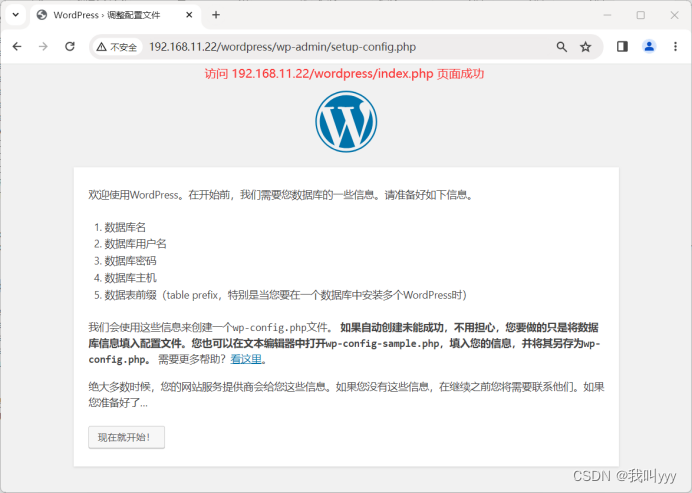
Docker之Dockerfile搭建lnmp
目录 一、搭建nginx 编辑 二、搭建Mysql(简略版) 三、搭建PHP 五、补充 主机名ip地址主要软件mysql2192.168.11.22Docker 代码示例 systemctl stop firewalld systemctl disable firewalld setenforce 0docker network create --subnet172.18.…...
排序算法——选择排序
一、介绍: 选择排序就是按照一定的顺序从选取第一个元素索引开始,将其储存在一个变量值中,根据排序规则比较后边每一个元素与这个元素的大小,根据排序规则需要,变量值的索引值进行替换,一轮遍历之后&#x…...

【数据结构C/C++】双向链表的增删改查
文章目录 CC408考研各数据结构C/C代码(Continually updating) 对我个人而言,在开发过程中使用的比较多的就是双向链表了。 很多重要的代码优化都会使用到基于双向链表实现的数据机构。 比如我们常用的HashMap,我们知道Key其实是无…...
Godot 添加Nuget 引用
前言 我的Godot 专栏 我在之前的文章中,解决了Visual Studio 如何去调试正在运行的Godot 程序。Godot 对于C# 的支持只剩下一个,那就是Nuget 添加。 Godot VisualStudio外部编辑器设置 添加Nuget Nuget 添加还是非常的容易的。我们直接添加一个最常用的…...

IC工程师职场必备《经典Verilog100多个代码案例》(附下载)
对于IC行业的人员而言,Verilog是最基础的入门,用于数字电路的系统设计,很多的岗位都会用到,可对算法级、门级、开关级等多种抽象设计层次进行建模。 Verilog由于其简单的语法,和C语言的相似性,目前被各大公…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

GraphRAG优化新思路-开源的ROGRAG框架
目前的如微软开源的GraphRAG的工作流程都较为复杂,难以孤立地评估各个组件的贡献,传统的检索方法在处理复杂推理任务时可能不够有效,特别是在需要理解实体间关系或多跳知识的情况下。先说结论,看完后感觉这个框架性能上不会比Grap…...
