CSS中的text-overflow属性详解 (控制文字在一行显示,超出部分加省略号)
- text-overflow: ellipsis; 表示当文本内容超出所在容器的宽度时,用省略号来代替超出的部分。
- white-space:nowrap; 表示文本不换行。
- overflow: hidden; 表示超出容器的内容将被隐藏。
将这三个加入需要控制的css的属性中,就能控制文字在一行显示,超出部分加省略号。
在网页开发中,文本内容长度超出限定宽度的情况非常常见。这时候,就需要使用text-overflow属性来处理文本内容的溢出问题。本文将对text-overflow属性的用法进行详细介绍,并结合实例来演示其使用方法。
text-overflow属性可以用于控制文本内容在容器宽度内的显示方式。它有三个属性值:
clip:默认值,表示文本溢出时被剪切隐藏。
ellipsis:表示文本溢出时显示省略号。
string:表示文本溢出时显示指定的字符串。
同时,为了确保文本内容能够在一行内完整显示,我们还需要使用white-space和overflow属性。其中,white-space属性用于控制文本如何进行换行,而overflow属性用于控制当文本内容超出容器限定宽度时的显示方式。
下面是一个例子,我们将一段文字放在一个固定宽度的容器中,并使用text-overflow属性来控制文本内容的显示方式:
<div class="container"><p class="text">这是一段超出限定宽度的文本内容</p>
</div><style>.container {width: 200px;border: 1px solid #000;}.text {text-overflow: ellipsis;white-space: nowrap;overflow: hidden;}
</style>在上面的代码中,我们将文本内容放在一个200像素宽的容器中,并设置text-overflow为ellipsis(表示使用省略号来处理文本内容的溢出),white-space为nowrap(表示不允许文本进行换行),overflow为hidden(表示当文本内容超出容器宽度时,隐藏超出部分)。
这样,当文本内容超出容器宽度时,就会显示省略号。如果要使用string值来处理文本溢出,可以在text-overflow属性中设置要显示的字符串。
总结:
text-overflow属性可以用于控制文本内容的显示方式,它有三个属性值:clip、ellipsis和string。同时,为了确保文本内容能够在一行内完整显示,我们还需要使用white-space和overflow属性来进行设置。
希望本文对大家学习CSS有所帮助,谢谢阅读!
相关文章:
)
CSS中的text-overflow属性详解 (控制文字在一行显示,超出部分加省略号)
text-overflow: ellipsis; 表示当文本内容超出所在容器的宽度时,用省略号来代替超出的部分。white-space:nowrap; 表示文本不换行。overflow: hidden; 表示超出容器的内容将被隐藏。 将这三个加入需要控制的css的属性中,就能控制文字在一行显示ÿ…...

基于pytorch实现模型剪枝
一,剪枝分类二,PyTorch 的剪枝三,总结参考资料一,剪枝分类 所谓模型剪枝,其实是一种从神经网络中移除"不必要"权重或偏差(weigths/bias)的模型压缩技术。关于什么参数才是“不必要的”,这是一个目前依然在研究的领域。 1.1,非结构化剪枝 非结构化剪枝(U…...

写出高质量的前端代码之消除代码中的重复
软件开发中,有个很重要的DRY原则,即Dont Repeat Yourself,也就是不要重复自己。 重复的代码会带来以下问题: 开发效率低,重复造轮子不同人开发的同一类功能,质量层次不齐修改问题时可能会遗漏,…...
怎么从零开始学黑客,黑客零基础怎么自学
很多朋友对成为黑客很感兴趣,很大原因是因为看到电影中黑客的情节觉的特别的酷,看到他们动动手指就能进入任何系统,还有很多走上黑客之路的朋友仅仅是因为自己的qq被盗了,或者游戏里的装备被别人偷了,想要自己盗回来&a…...
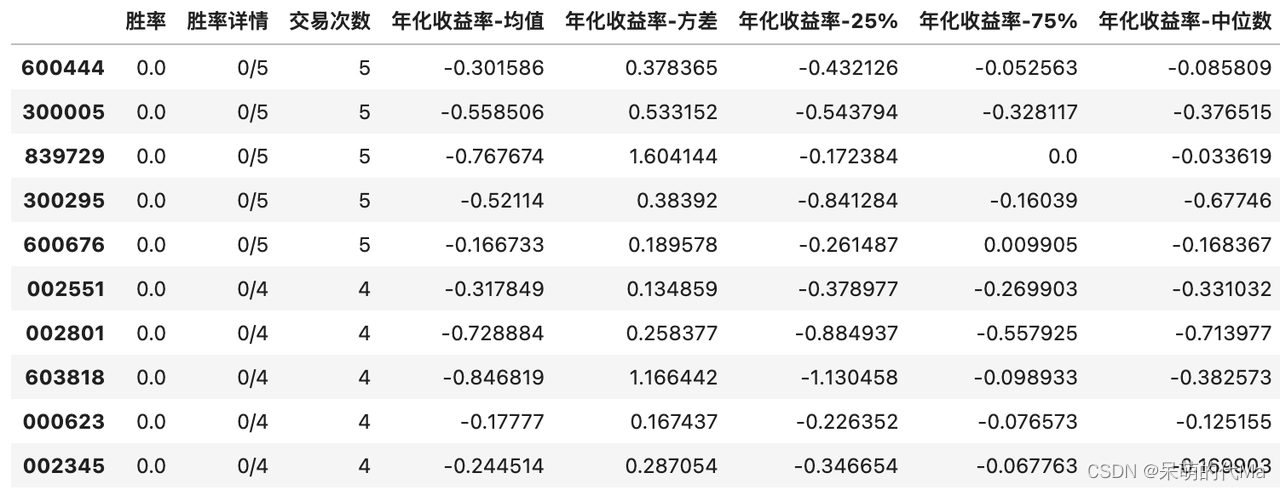
量化择时——资金流择时策略(第1部分—因子测算)
文章目录资金流模型概述资金流模型的有效性逻辑资金流向指标MFI(Money Flow Index)MFI指标测算测算规则测算结论资金流模型概述 通常,资金流是一种反映股票供给信息的指标,宏观上来讲,我们知道一个道理:僧…...

Openwrt中动态IPV6 防火墙的正确设置方法
环境:光猫桥接公网IPV6 问题:动态IPV6地址不知道怎么设置防火墙 解决办法:模糊匹配前缀,特定后缀 背景:将家中光猫桥接后,获得了公网的IPV6地址,可以从外部用IPV6访问家中的设备,但I…...

JS的基本数据类型和引用数据类型
ES6 引入了一种新的原始数据类型 Symbol,表示独一无二的值。它是 JavaScript 语言的第七种数据类型,前六种是:Undefined、Null、布尔值(Boolean)、字符串(String)、数值(Number&…...
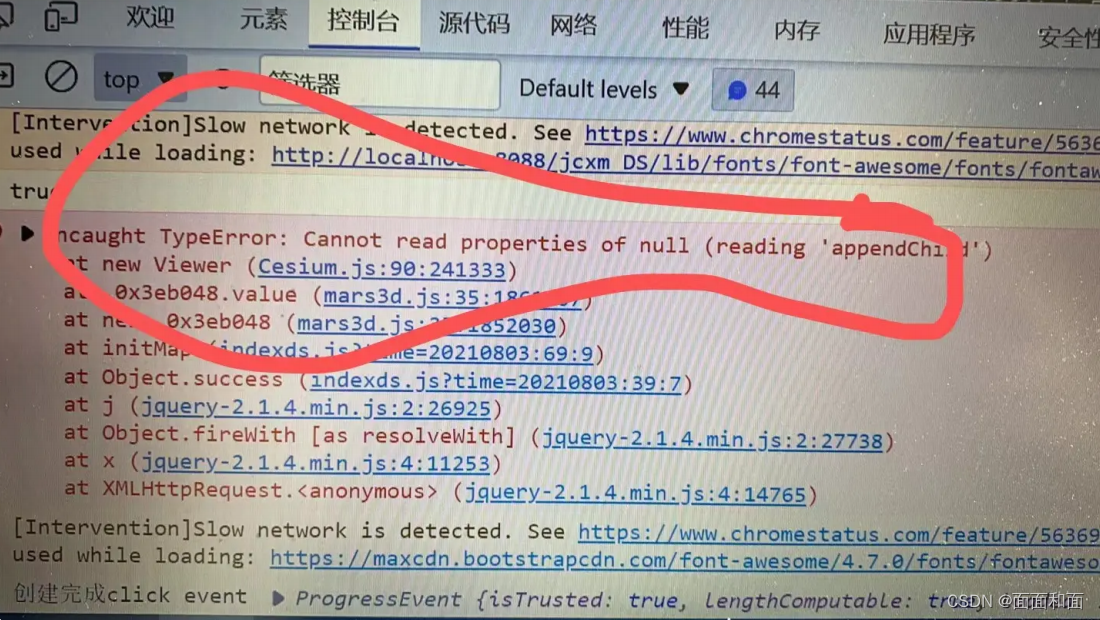
mars3d基础项⽬常⻅报错
1.在⼤家使⽤mars3d基础项⽬的时候经常遇到这个报错,截图如下 回答: 1.原因是因为使⽤了cnpm安装依赖,导致了⼀些依赖问题 2.解决⽅式也很简答,重新使⽤ npm 或 yarn 或 pnpm安装依赖即可 2.本地加载地图时,出现报错回…...
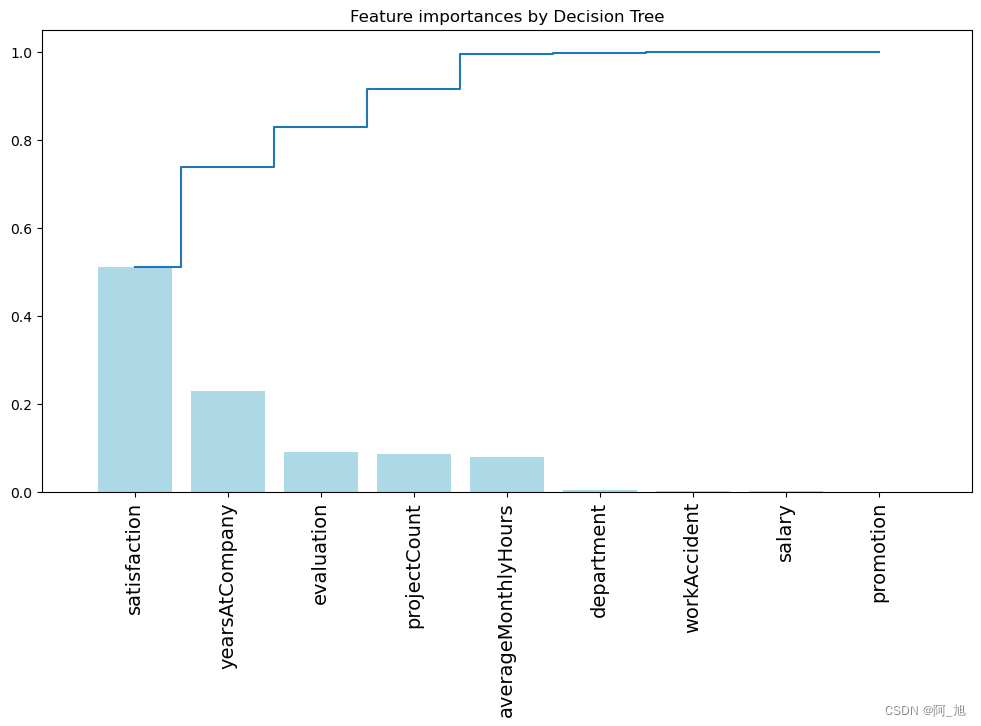
【阿旭机器学习实战】【35】员工离职率预测---决策树与随机森林预测
【阿旭机器学习实战】系列文章主要介绍机器学习的各种算法模型及其实战案例,欢迎点赞,关注共同学习交流。 本文的主要任务是通过决策树与随机森林模型预测一个员工离职的可能性并帮助人事部门理解员工为何离职。 目录1.获取数据2.数据预处理3.分析数据3.…...

Python学习-----模块4.0(json字符串与json模块)
目录 1.json简介: 2.json对象 3.json模块 (1)json.dumps() 函数 (2)json.dumps() 函数 (3)json.loads() 函数 (4) json.load() 函数 4.总结: 1.json简介: SON(…...

open3d最大平面检测,平面分割
1.点云读入 读入文件(配套点云下载链接) # 读取点云 pcd o3d.io.read_point_cloud("point_cloud_00000.ply")配套点云颜色为白色,open3d的点云显示默认背景为白色,所以将点云颜色更改为黑色 pcd.colors o3d.utilit…...
)
【C++】4.类和对象(下)
1.再谈构造函数 1赋值 class Date { public:Date(int year, int month, int day){_year year;_month month;_day day;}private:int _year;int _month;int _day; };构造函数体中的语句只能将其称作为赋初值,而不能称作初始化。因为初始化只能初始化一次…...
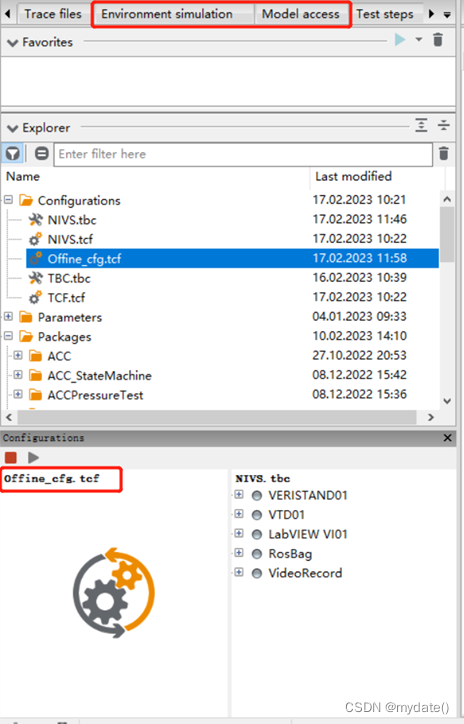
自动驾驶仿真:ECU TEST 、VTD、VERISTAND连接配置
文章目录一、ECU TEST 连接配置简介二、TBC配置 test bench configuration三、TCF配置 test configuration提示:以下是本篇文章正文内容,下面案例可供参考 一、ECU TEST 连接配置简介 1、ECU TEST(简称ET),用于HIL仿…...

postgres数据库连接管理
1.连接命令psql -d postgres -h 10.0.0.51. -p 1921 -U postgres(-d指定数据库名字)2.pg防火墙介绍(pg实例层面的权限控制)pg_hba.conf文件配置文件分为5部分:配置示例#TYPE DATABASE USER ADDRESS METHODhost all loc…...

【华为OD机试模拟题】用 C++ 实现 - 环中最长子串(2023.Q1)
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...

Spring:@Async 注解和AsyncResult与CompletableFuture使用
Async概述 Spring中用Async注解标记的方法,称为异步方法,它会在调用方的当前线程之外的独立的线程中执行, 其实就相当于我们自己new Thread(()-> System.out.println("hello world !"))这样在另一个线程中去执行相应的业务逻辑…...

tidb ptca,ptcp考证
PingCAP 认证 TiDB 数据库专员 V6 考试(2023-02-23)https://learn.pingcap.com/learner/exam-market/list?categoryPCTA PingCAP 认证 TiDB 数据库管理专家(PCTP - DBA)认证考试范围指引 - ☄️ 学习与认证 - TiDB 的问答社区:lo…...
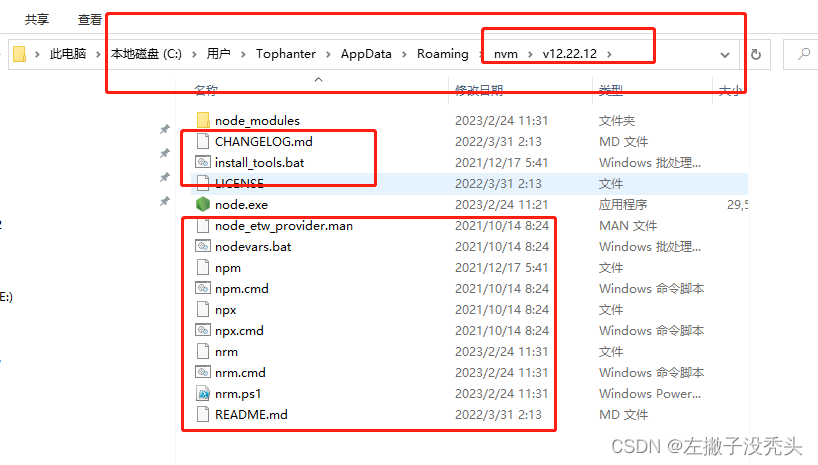
关于用windows开发遇到的各种乌龙事件之node版本管理---nvm install node之后 npm 找不到的问题
友情提醒,开发最好用nvm控制node版本 nrm 控制镜像源,能少掉很多头发开发过程中技术迭代更新的时候最要老命的就是 历史项目的node版本没有记录,导致开启旧项目的时候就会报错。尤其是npm 升级到8.x.x以后,各种版本不兼容。 真…...
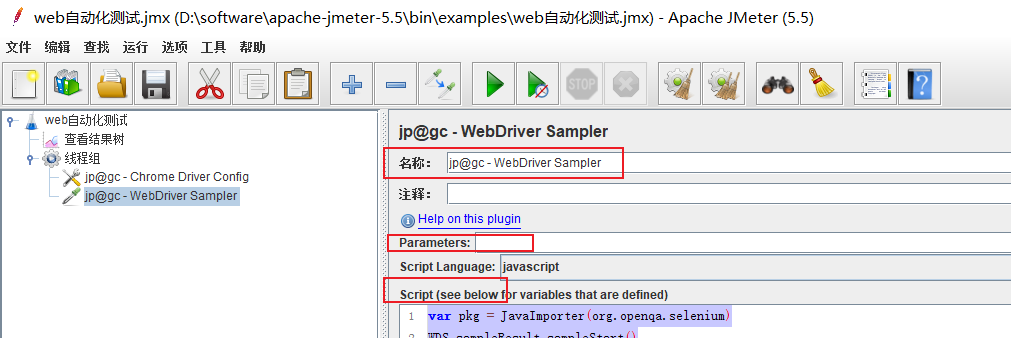
JMeter做UI自动化
插件安装搜插件selenium,安装添加config添加线程组右键线程组->添加->配置元件->jpgc - Chrome Driver Configoption和proxy不解释了添加Sampler右键线程组->添加->取样器->jpgc - WebDriver Samplerscript language 选择:JavaScript&…...
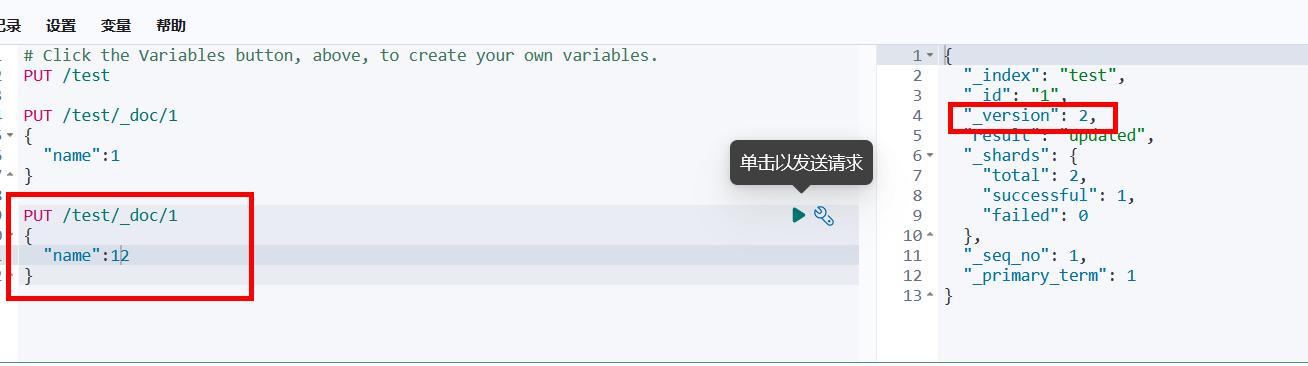
Kibana与Elasticsearch
下载与安装Kibanahttps://www.elastic.co/cn/downloads/kibanaKibana的版本与Elasticsearch的版本是一致的,使用方法也和Elasticsearch一致。由于我的英文不是特别好,我们找到config/kibana.yml末尾添加i18n.locale: "zh-CN" ,汉化…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...
