C语言编程实现只有一个未知数的两个多项式合并的程序
背景:
直接看题目把!就是C语言写两个多项式多项式合并
题目要求:
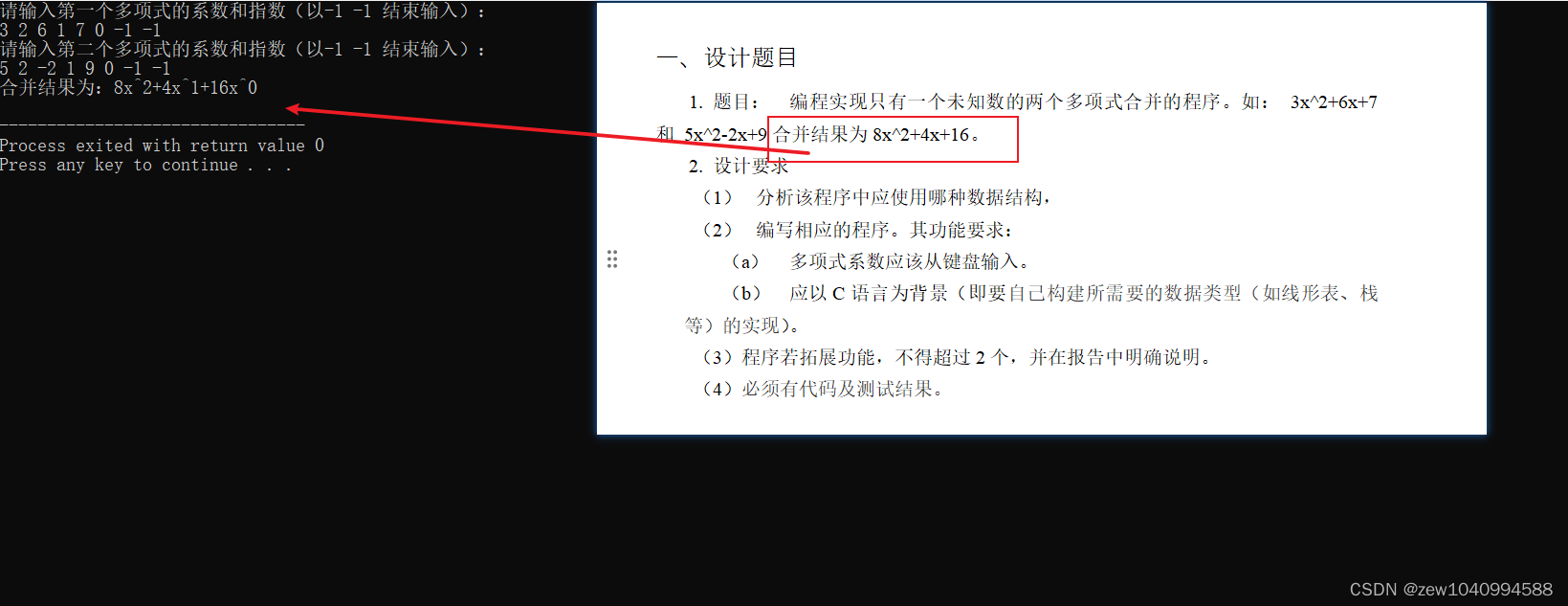
1. 题目: 编程实现只有一个未知数的两个多项式合并的程序。如: 3x^2+6x+7 和 5x^2-2x+9合并结果为8x^2+4x+16。
2. 设计要求
(1) 分析该程序中应使用哪种数据结构,
(2) 编写相应的程序。其功能要求:
(a) 多项式系数应该从键盘输入。
(b) 应以C语言为背景(即要自己构建所需要的数据类型(如线形表、栈等)的实现)。
(3)程序若拓展功能,不得超过2个,并在报告中明确说明。
(4)必须有代码及测试结果。
代码效果:
简单粗暴上效果图!
代码实现了动态获取多项式系数和指数,支持用户输入两个自定义参数,然后程序会合并用户输入的参数,给出运行结果。
主要代码:
所使用的结构体
//联系请加V:zew1040994588struct Term {int coefficient; // 系数int exponent; // 指数struct Term* next;
};main函数
//联系请加V:zew1040994588int main() {Polynomial* poly1 = NULL;Polynomial* poly2 = NULL;Polynomial* result = NULL;int coefficient, exponent;printf("请输入第一个多项式的系数和指数(以-1 -1 结束输入):\n");while (scanf("%d %d", &coefficient, &exponent) == 2 && (coefficient != -1 || exponent != -1)) {insertTerm(&poly1, coefficient, exponent);}printf("请输入第二个多项式的系数和指数(以-1 -1 结束输入):\n");while (scanf("%d %d", &coefficient, &exponent) == 2 && (coefficient != -1 || exponent != -1)) {insertTerm(&poly2, coefficient, exponent);}mergePolynomials(poly1, poly2, &result);printf("合并结果为:");printPolynomial(result);destroyPolynomial(poly1);destroyPolynomial(poly2);destroyPolynomial(result);return 0;
}相关文章:

C语言编程实现只有一个未知数的两个多项式合并的程序
背景: 直接看题目把!就是C语言写两个多项式多项式合并 题目要求: 1. 题目: 编程实现只有一个未知数的两个多项式合并的程序。如: 3x^26x7 和 5x^2-2x9合并结果为8x^24x16。 2. 设计要求 (1)…...
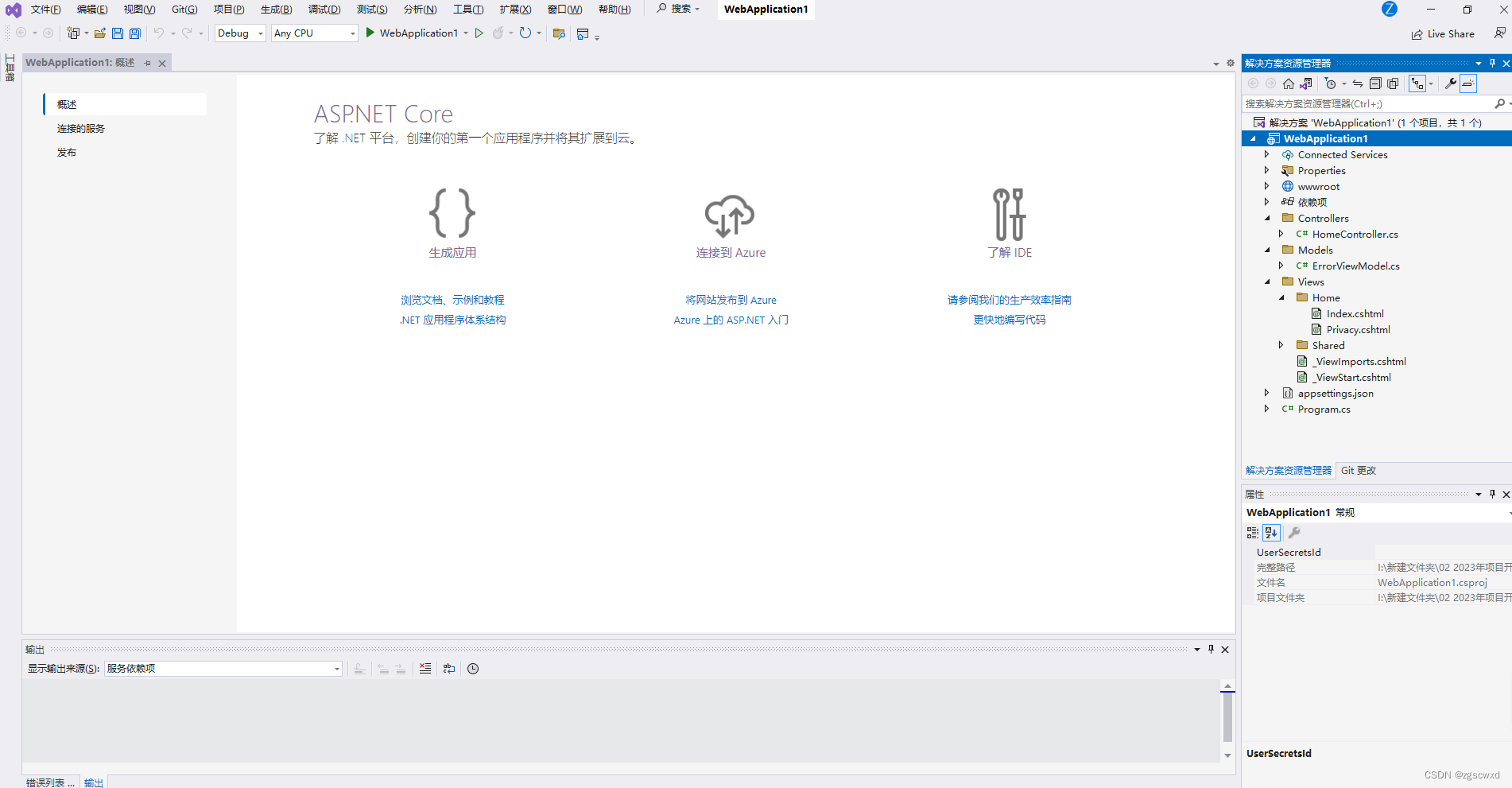
C# .net创建一个MVC框架工程
二、C# .net创建一个MVC框架工程 1.步骤 首先打开VS ,然后点击创建新项目 在三个选项框中输入我们需要的项目条件 最后一步创建完毕 创建会在资源解决方案生成如图:...
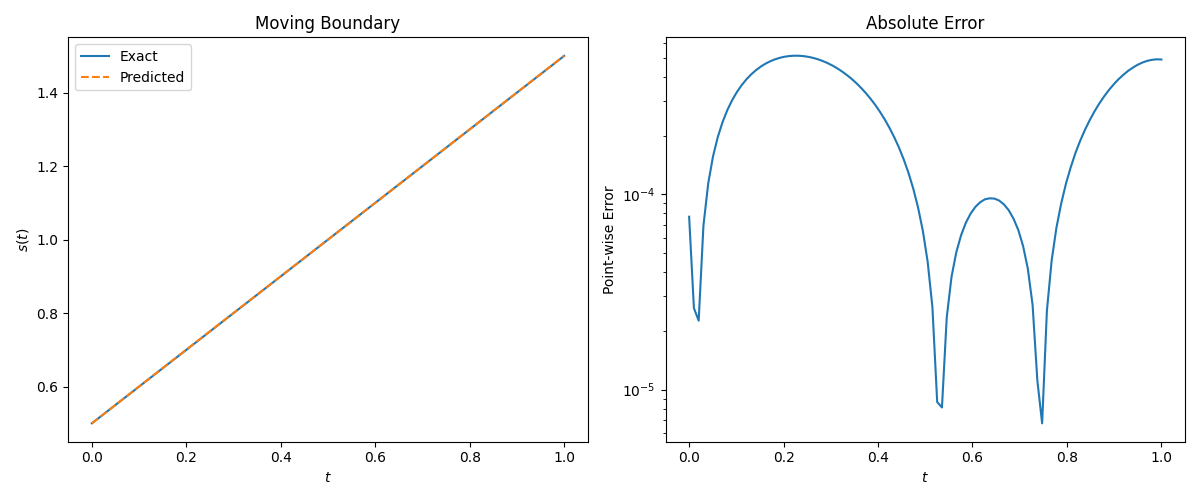
Deep learning of free boundary and Stefan problems论文阅读复现
Deep learning of free boundary and Stefan problems论文阅读复现 摘要1. 一维一相Stefan问题1.1 Direct Stefan problem1.2 Inverse Type I1.3 Inverse Type II 2. 一维二相Stefan问题2.1 Direct Stefan problem2.2 Inverse Type I2.3 Inverse Type II 3. 二维一相Stefan问题…...
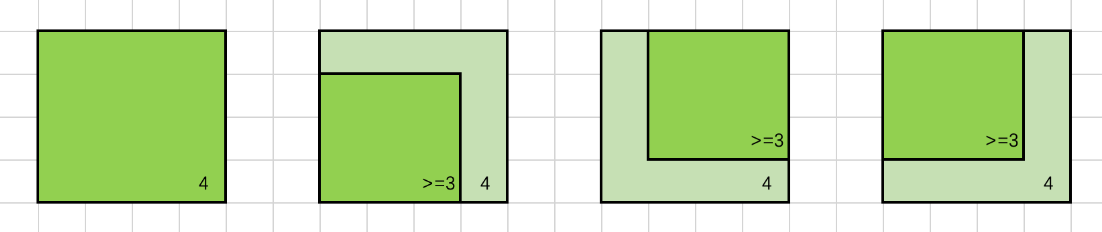
LeetCode 1277. 统计全为 1 的正方形子矩阵【动态规划】1613
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

测试部门来了个00后卷王之王,老油条感叹真干不过,但是...
都说00后躺平了,但是有一说一,该卷的还是卷。 这不,前段时间我们公司来了个00后,工作都没两年,跳槽到我们公司起薪18K,都快接近我了。后来才知道人家是个卷王,从早干到晚就差搬张床到工位睡觉了…...

360 G800行车记录仪,不使用降压线如何开机,8芯插头的定义。
G800记录仪的插头是这样的,图中标出了线的颜色。其中红色为常电V,黑色为GND负极,黄色为ACC受车是否启动控制。 这个记录仪原装的电源线没有降压功能,所以这里的V是12V。 记录仪内部有电源板,负责将12V降压为5V。 如果…...
vue2踩坑之项目:Swiper轮播图使用
首先安装swiper插件 npm i swiper5 安装出现错误:npm ERR npm ERR! code ERESOLVE npm ERR! ERESOLVE could not resolve npm ERR! npm ERR! While resolving: vue/eslint-config-standard6.1.0 npm ERR! Found: eslint-plugin-vue8.7.1 npm ERR! node_modules/esl…...

python经典百题之分桃子
题目:海滩上有一堆桃子,五只猴子来分。第一只猴子把这堆桃子平均分为五份,多了一个,这只 猴子把多的一个扔入海中,拿走了一份。第二只猴子把剩下的桃子又平均分成五份,又多了 一个,它同样把多的一个扔入海中…...
vscode ssh linux C++ 程序调试
vscode调试c++程序相比vs2022要复杂很多,vs2022可以"一键运行调试",vscode则需要自己配置。 vscode调试程序时,会在当前工作目录产生.vscode 目录, 该目录有两个重要文件launch.json和tasks.json, 下面介绍两种调试方法: 手动调试和自动调试。 手动调试 不管…...

VUE和Angular有哪些区别?
Vue.js和Angular是两个流行的前端JavaScript框架,它们有一些明显的区别,包括以下几个方面: 1、语言和工具链的选择: Vue.js使用HTML、JavaScript和CSS来创建组件,使得它更容易学习,因为它使用了常见的Web…...
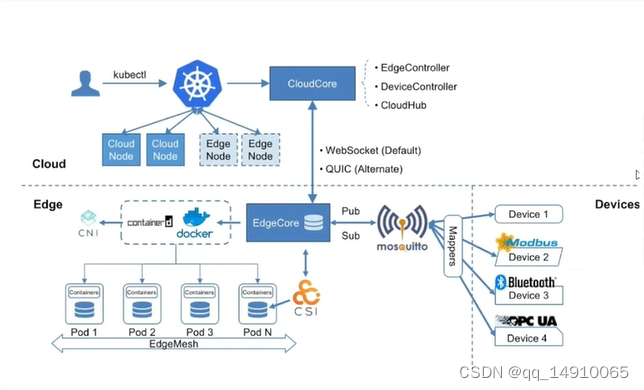
云原生边缘计算KubeEdge安装配置(二)
1. K8S集群部署,可以参考如下博客 请安装k8s集群,centos安装k8s集群 请安装k8s集群,ubuntu安装k8s集群 请安装kubeedge cloudcore centos安装K8S 2.安装kubEedge 2.1 编辑kube-proxy使用ipvs代理 kubectl edit configmaps kube-proxy -…...

SQL多表设计--一对多(外键)
-- 完成部门和员工的-- 选择当前db03 这个数据库use db03;-- 查看当前选中的数据库select database();-- 创建员工表create table tb_emp (id int unsigned primary key auto_increment comment ID,username varchar(20) not null unique comment 用户名,password varchar(32)…...
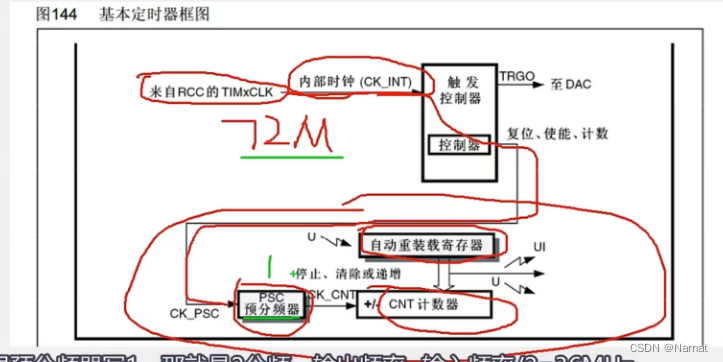
Stm32_标准库_9_TIM
频率(HZ)是频率的基本单位1HZ是1s的倒数 STM32F103C8T6一般情况给定时器的内部时钟都是72MHz(系统主频率) TIM基本构成 计数器、预分频器、自动化重装 // 都是16位其中计数器、自动化重装,都是16位换算成10进制范围为[0, 655536] 时间 1 /…...

283. 移动零
283. 移动零 原题 /** 左指针左边均为非零数; 右指针左边直到左指针处均为零。*/ class Solution {public void moveZeroes(int[] nums) {int left 0;int right 0;while(right<nums.length){if(nums[right]!0){swap(nums,left,right);left;}right;}}public v…...

用 HTTP 提交数据,基本就这 5 种方式
网页开发中,向服务端提交数据是一个基本功能,工作中会大量用 xhr/fetch 的 api 或者 axios 这种封装了一层的库来做。 可能大家都写过很多 http/https 相关的代码,但是又没有梳理下它们有哪几种呢? 其实通过 http/https 向服务端…...
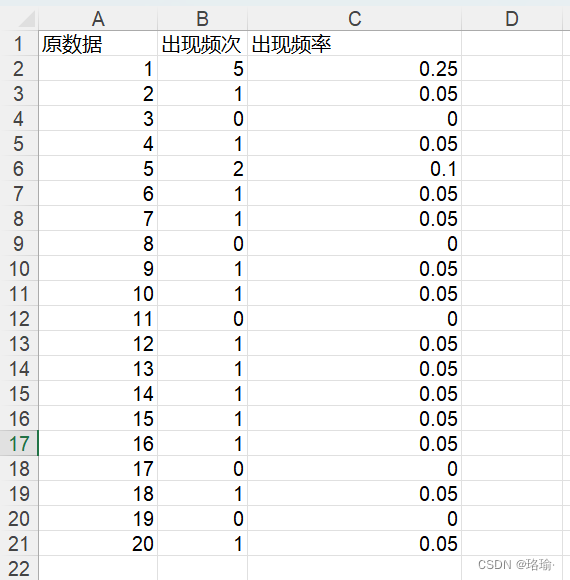
基于matlab统计Excel文件一列数据中每个数字出现的频次和频率
一、需求描述 如上表所示,在excel文件中,有一列数,统计出该列数中,每个数出现的次数和频率。最后,将统计结果输出到新的excel文件中。 二、程序讲解 第一步:选择excel文件; [Filename, Pathn…...
近期分享学习心得3
1、全屏组件封装 先看之前大屏端的监控部分全屏代码 整块全屏代码 常规流是下面这种 //进入全屏 function full(ele) {//if (ele.requestFullscreen) {// ele.requestFullscreen();//} else if (ele.mozRequestFullScreen) {// ele.mozRequestFullScreen();//} el…...
前端uniapp如何修改下拉框uni-data-select下面的uni-icons插件自带的图片【修改uniapp自带源码图片/图标】
目录 未改前图片未改前源码未改前通过top和bottom 和修改后图片转在线base64大功告成最后 未改前图片 未改前源码 然后注释掉插件带的代码,下面要的 未改前通过top和bottom 和修改后 找到uni-icons源码插件里面样式 图片转在线base64 地址 https://the-x.cn/b…...

【计算机基础】Git系列3:常用操作
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...
有哪些值得推荐的Java 练手项目?
大家好,我是 jonssonyan 我是一名 Java 后端程序员,偶尔也会写一写前端,主要的技术栈是 JavaSpringBootMySQLRedisVue.js,基于我学过的技术认真的对每个分享的项目进行鉴别,今天就和大家分享我曾经用来学习的开源项目…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...
