基于WTMM算法的图像多重分形谱计算matlab仿真
目录
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
4.1、WTMM算法概述
4.2、WTMM算法原理
4.2.1 二维小波变换
4.2.2 模极大值检测
4.2.3 多重分形谱计算
5.算法完整程序工程
1.算法运行效果图预览



2.算法运行软件版本
matlab2022a
3.部分核心程序
.........................................................................
%%
%对保存的多张图片读取并调用WTMM方法求图像的多重分形谱,对得到的结果保存其特征值
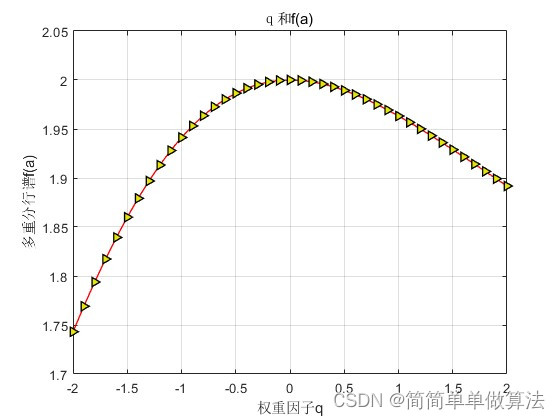
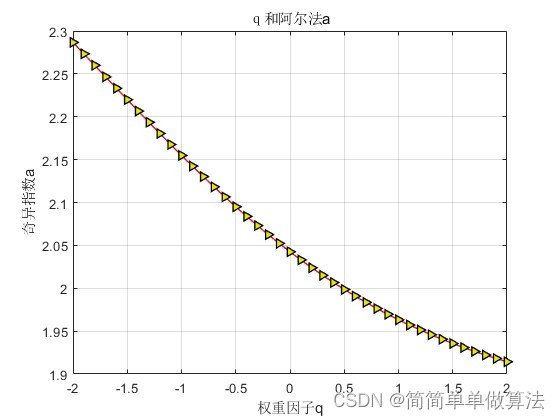
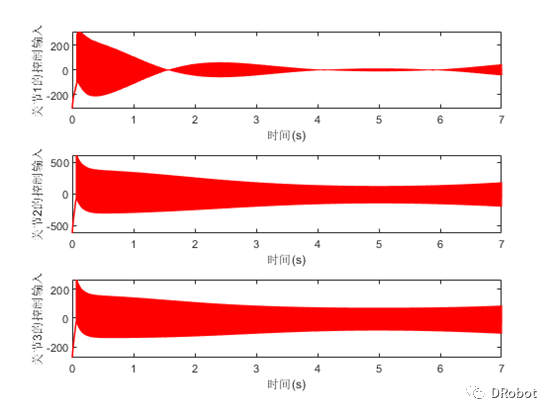
if sel == 1k = 1;for i=1:2*n1*n2;if i<=n1*n2k = i;folder = 'save_images\1\';lists = dir('save_images\1\*.jpg'); endif i<=2*n1*n2 & i>n1*n2k = i - n1*n2;folder = 'save_images\2\';lists = dir('save_images\2\*.jpg'); end i%read an imageI = imread(fullfile(folder,lists(k).name));%调用分形函数[qt,rt,ft,fft,Dt,feature_data] = func_Wavelet_multifractal(I);q{i} = qt;r{i} = rt; f{i} = ft; ff{i} = fft; D{i} = Dt;Feature{i} = feature_data;endsave result.mat q r f ff D FeatureK = 120;figure;plot(r{K},f{K},'-r>',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.9,0.0]);xlabel('奇异指数a');ylabel('多重分行谱f(a)') grid on;figure;plot(q{K}+2,D{K},'-r>',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.9,0.0]);xlabel('q');ylabel('D(q)') grid on;figureplot(q{K},r{K},'-r>',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.9,0.0]);title('q和阿尔法a'); xlabel('权重因子q');ylabel('奇异指数a');grid on;figure;plot(q{K},f{K},'-r>',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.9,0.0]);title('q和f(a) '); xlabel('权重因子q');ylabel('多重分行谱f(a)'); grid on;
end %%
%调用分类器对特征参数进行分类
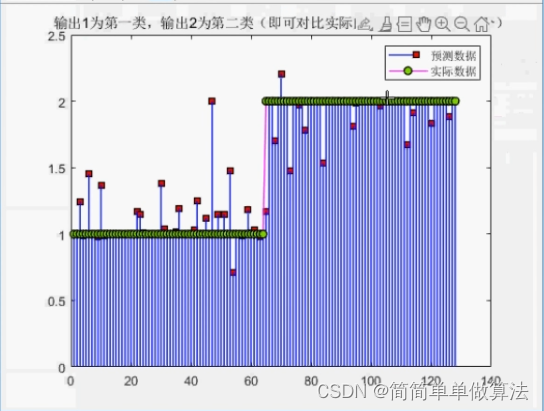
if sel == 0load result.mat %q r f ff FeatureK = 120;figure;plot(r{K},f{K},'-r>',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.9,0.0]);xlabel('奇异指数a');ylabel('多重分行谱f(a)') grid on;figure;plot(q{K}+2,D{K},'-r>',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.9,0.0]);xlabel('q');ylabel('D(q)') grid on;figureplot(q{K},r{K},'-r>',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.9,0.0]);title('q和阿尔法a'); xlabel('权重因子q');ylabel('奇异指数a');grid on;figure;plot(q{K},f{K},'-r>',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.9,0.0]);title('q和f(a) '); xlabel('权重因子q');ylabel('多重分行谱f(a)'); grid on; for i = 1:length(Feature)P(i) = Feature{i}(3);end T = [1*ones(1,length(Feature)/2),2*ones(1,length(Feature)/2)];t1 = clock; %计时开始net = fitnet(65);net.trainParam.epochs = 1000; %设置训练次数net.trainParam.goal = 0.0001; %设置性能函数net.trainParam.show = 1; %每10显示net.trainParam.Ir = 0.005; %设置学习速率net = train(net,P,T); %训练BP网络datat = etime(clock,t1);Nets = net;view(Nets);figure;plot(P,'b-*');y = sim(net,P); figure;stem(y,'-bs',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.0,0.0]);hold onplot(T,'-mo',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.5,0.9,0.0]);hold onlegend('预测数据','实际数据');title('输出1为第一类,输出2为第二类(即可对比实际的健康部分和肿瘤部分)');disp('预测正确率');error = 0;for i = 1:length(y)if i <= length(y)/2 if y(i) > 1.5error = error + 1;endelseif y(i) < 1.5error = error + 1;end endend1-error/length(y)
end
17_003m4.算法理论概述
基于WTMM算法的图像多重分形谱计算是一种利用小波变换模极大值(WTMM)方法,对图像进行多重分形分析的方法。下面将详细介绍这种方法的原理和数学公式。
4.1、WTMM算法概述
分形理论是一种研究自然界中不规则、复杂现象的数学工具,而多重分形则是分形理论的一个重要分支,用于描述具有不同奇异程度的分形结构。在图像处理中,多重分形分析可以帮助我们更好地理解图像的纹理、边缘等特征,以及它们在不同尺度下的表现。
WTMM算法是一种基于小波变换模极大值的方法,用于计算图像的多重分形谱。该方法主要利用小波变换对图像进行多尺度分解,提取出图像在不同尺度下的边缘信息。然后,通过对这些边缘信息进行统计分析,计算出图像的多重分形谱。
具体来说,WTMM算法的计算步骤如下:
- 对图像进行二维小波变换,得到一系列小波系数。
- 对每个尺度下的小波系数进行模极大值检测,提取出图像的边缘信息。
- 对提取出的边缘信息进行统计分析,计算出图像的多重分形谱。
4.2、WTMM算法原理
WTMM算法的数学公式主要包括以下几个部分:
4.2.1 二维小波变换
对图像f(x,y)进行二维小波变换,可以得到一系列小波系数Wf(x,y),其中下标f表示小波变换的类型,如Haar小波、Daubechies小波等。二维小波变换的数学公式可以表示为:
Wf(x,y)=∫∫f(u,v)ψf(x−u,y−v)dudvWf(x,y) = \int \int f(u,v) \psi_f(x-u,y-v) du dvWf(x,y)=∫∫f(u,v)ψf(x−u,y−v)dudv
其中,ψf(x,y)是小波基函数。
4.2.2 模极大值检测
对每个尺度下的小波系数进行模极大值检测,可以提取出图像的边缘信息。具体地,对于每个像素位置(x,y),如果满足以下两个条件:
|Wf(x,y)|≥|Wf(x+1,y)|,|Wf(x,y)|≥|Wf(x−1,y)|,|Wf(x,y)|≥|Wf(x,y+1)|,|Wf(x,y)|≥|Wf(x,y−1)||W_f(x,y)| \geq |W_f(x+1,y)|, |W_f(x,y)| \geq |W_f(x-1,y)|,|W_f(x,y)| \geq |W_f(x,y+1)|, |W_f(x,y)| \geq |W_f(x,y-1)||Wf(x,y)|≥|Wf(x+1,y)|,|Wf(x,y)|≥|Wf(x−1,y)|,|Wf(x,y)|≥|Wf(x,y+1)|,|Wf(x,y)|≥|Wf(x,y−1)|
则称该像素位置为模极大值点。
4.2.3 多重分形谱计算
通过对提取出的边缘信息进行统计分析,可以计算出图像的多重分形谱。具体地,可以用以下公式计算多重分形谱:
α=limε→0log|Wf(x,y)|logε\alpha = \lim_{\varepsilon \to 0} \frac{\log |W_f(x,y)|}{\log \varepsilon}α=limε→0logεlog|Wf(x,y)|
其中,ε是小波变换的尺度参数,α是奇异指数,用于描述图像在不同尺度下的奇异程度。通过对所有模极大值点的奇异指数进行统计分析,可以得到图像的多重分形谱。
5.算法完整程序工程
OOOOO
OOO
O
相关文章:

基于WTMM算法的图像多重分形谱计算matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 4.1、WTMM算法概述 4.2、WTMM算法原理 4.2.1 二维小波变换 4.2.2 模极大值检测 4.2.3 多重分形谱计算 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部…...

VR全景展示带来旅游新体验,助力旅游业发展!
引言: VR(虚拟现实)技术正以惊人的速度改变着各行各业,在旅游业中,VR全景展示也展现了其惊人的影响力,为景区带来了全新的宣传机会和游客体验。 一.什么是VR全景展示? VR全景展示是…...
Xcode 15 编译出错问题解决
正常升级xcode 15以后发现原来没有出现报错的代码,现在出现了编译错误。(如果没有出现请忽略)下面教你如何解决这个问题。 1、pod update更新cocoapods,因为其根据xcode15做了很多的更新,保证cocoapods是最新的。 千…...
基于指数趋近律的机器人滑模轨迹跟踪控制算法及MATLAB仿真
机械手是工业制造领域中应用最广泛的自动化机械设备,广泛应用于工业制造、医疗、军工、半导体制造、太空探索等领域。它们虽然形式不同,但都有一个共同的特点,即能够接受指令,并能准确定位到三维(或二维)空间的某一点进行工作。由…...
华为云API自然语言处理的魅力—AI情感分析、文本分析
云服务、API、SDK,调试,查看,我都行 阅读短文您可以学习到:人工智能AI自言语言的情感分析、文本分词、文本翻译 1 IntelliJ IDEA 之API插件介绍 API插件支持 VS Code IDE、IntelliJ IDEA等平台、以及华为云自研 CodeArts IDE&a…...

微擎小程序获取不到头像和昵称解决方案
这是一个使用微擎小程序的代码示例,其中包含了获取用户头像和昵称的功能。以下是解决方案: 首先,在<button>标签上添加open-type"chooseAvatar"属性,并绑定bindchooseavatar事件: <button class&qu…...
Qt 对界面类重命名的步骤
有些时候因为一些原因,需要修改Qt中创建的界面类,修改的地方比较多,一定要留意有没有修改完全,否则会出现各种奇怪报错。 比如,将MainWindow界面类名修改为lb_logdisplay 修改步骤: 修改文件名:…...
使用docker搭建nacos单机、集群 + mysql
单机搭建 1 拉取mysql镜像 docker pull mysql:5.7.40 2 启动mysql容器 docker run -d --namemysql-server -p 3306:3306 -v mysql-data:/var/lib/mysql -e MYSQL_ROOT_PASSWORD123456 mysql:5.7.40 3 执行nacos的数据库脚本 /* * Copyright 1999-2018 Alibaba Group Holding L…...
FreeRTOS自我救赎2之基本工程建立
System Core 1.System Core >SYS 2.System Core >RCC 3.System Core >NVIC Middleware Middleware >FREERTOS Clock configuration Project Manager 在编译生成的代码前需要找一个与芯片对应的启动文件,启动文件添加进来,编译就没问题了...
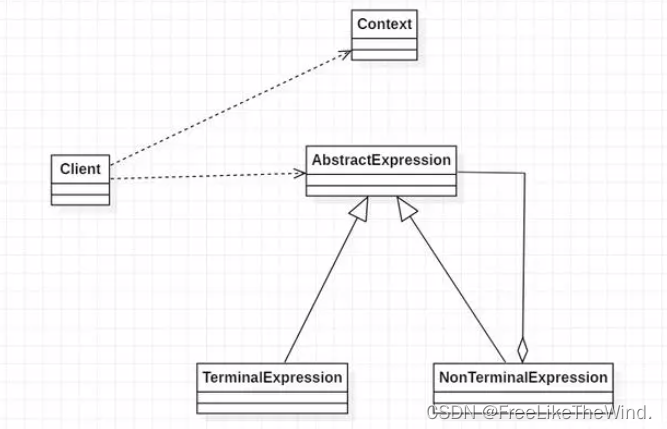
【C++设计模式之解释器模式:行为型】分析及示例
简介 解释器模式(Interpreter Pattern)是一种行为型设计模式,它提供了一种解决问题的方法,通过定义语言的文法规则,解释并执行特定的语言表达式。 解释器模式通过使用表达式和解释器,将文法规则中的句子逐…...
35 WEB漏洞-逻辑越权之找回机制及接口安全
目录 找回重置机制接口调用乱用演示案例绑定手机验证码逻辑-Rep状态值篡改-实例某APP短信轰炸接口乱用-实例接口调用发包 文章分享:https://www.cnblogs.com/zhengna/p/15655691.html 有支付接口、短信发送接口,邮箱的发送接口等等,在接口这…...

黑豹程序员-架构师学习路线图-百科:JSON替代XML
文章目录 1、数据交换之王2、XML的起源3、JSON诞生4、什么是JSON 1、数据交换之王 最早多个软件之间使用txt进行信息交互,缺点:纯文本,无法了解其结构;之后使用信令,如:电话的信令(拨号、接听、…...
)
考研人考研魂——英语单词篇(20231009)
下一站,上岸 consoleconsistentconsistconstituteconstitutionconstituentconstructdistinctdistinguishdistinctionconstantconstrainfruitfulfulfillfundfunctionfrustrateevidencefundamentalevilevidentenvironmententertainmententertainenterprisemonotonousm…...
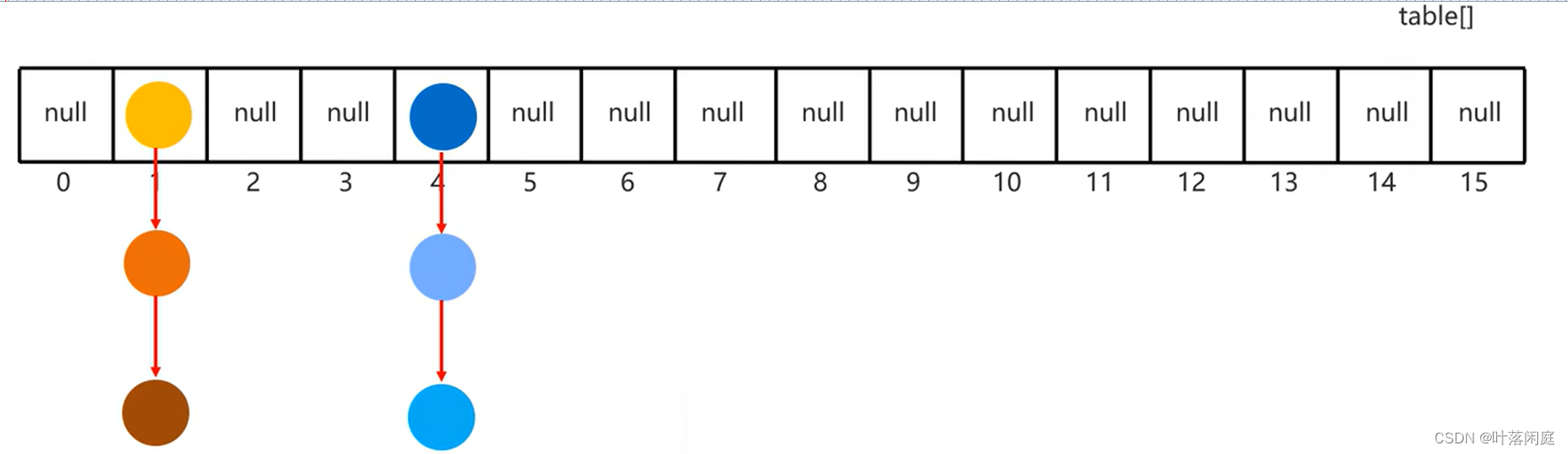
【数据结构】HashSet的底层数据结构
🐌个人主页: 🐌 叶落闲庭 💨我的专栏:💨 c语言 数据结构 javaEE 操作系统 Redis 石可破也,而不可夺坚;丹可磨也,而不可夺赤。 HashSet 一、 HashSet 集合的底层数据结构二…...
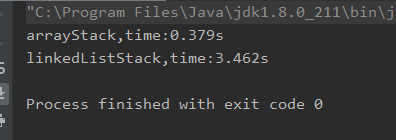
数据结构与算法(七)--使用链表实现栈
一、前言 之前我们已经学习了链表的所有操作及其时间复杂度分析,我们可以了解到对于链表头的相关操作基本都是O(1)的,例如链表头增加、删除元素,查询元素等等。那我们其实有一个数据结构其实可以完美利用到这些操作的特点,都是在…...

分布式事务详解
摘要 分布式事务主要包括2pc、3pc、消息事务。 2pc指两阶段提交: 第一阶段是准备阶段:所有事务参与者检查执行能力并锁定对应资源,准备完成后将状态告知协调者。第二集段是提交状态:事务参与者全部准备好后,协调者发…...

车载通信架构 —— DDS协议介绍
车载通信架构 —— DDS协议介绍 我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和…...

nginx根据不同的客户端设备进行转发请求——筑梦之路
这里主要介绍七层负载方式实现。 环境说明: pc端 web-1 苹果ios端 web-2 安卓Android端 web-3 负载均衡 web-lb 配置示例: pc端: server {listen 9000; #监听9000server_name pc.xxx.com;charset utf-8;location / {root /…...
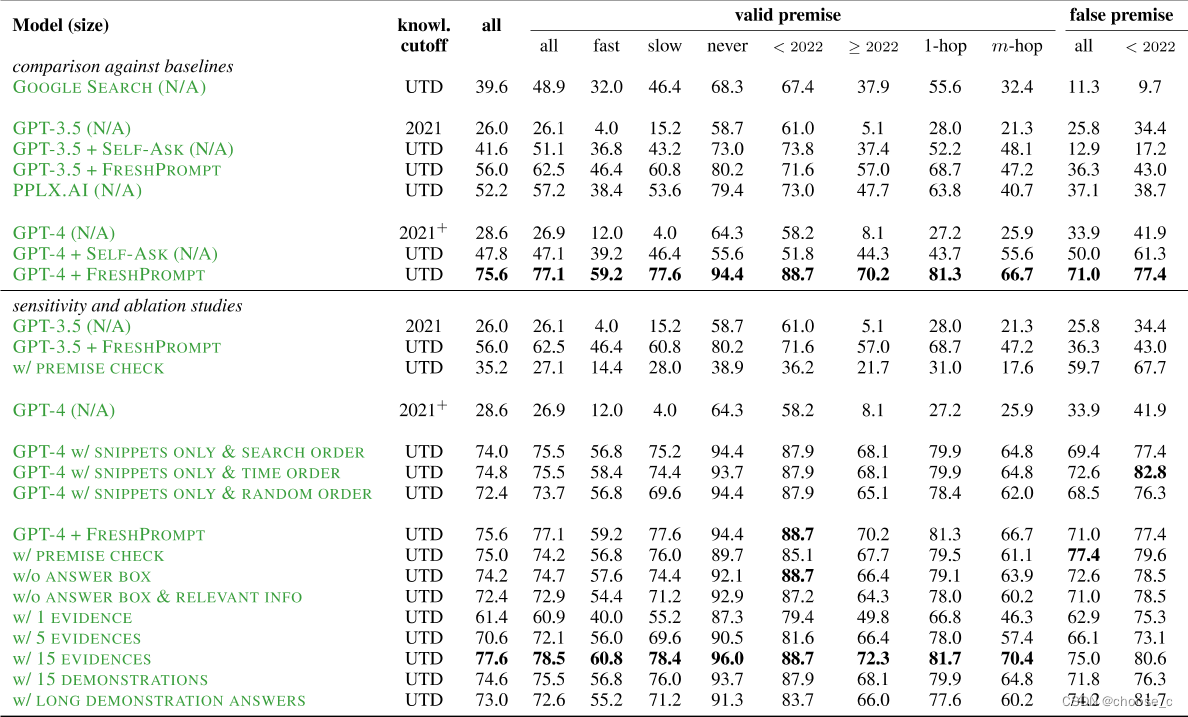
增强LLM:使用搜索引擎缓解大模型幻觉问题
论文题目:FRESHLLMS:REFRESHING LARGE LANGUAGE MODELS WITH SEARCH ENGINE AUGMENTATION 论文地址:https://arxiv.org/pdf/2310.03214.pdf 论文由Google、University of Massachusetts Amherst、OpenAI联合发布。 大部分大语言模型只会训练一次&#…...

WPF向Avalonia迁移(一、一些通用迁移项目)
通用变更 WPF:Visibility 其他参考文档 WPF: <TextBlock Visibility"Visible"/><TextBlock Visibility"Collapsed"/><TextBlock Visibility"Hidden"/>Avalonia : <TextBlock IsVisib…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
