Python每日一练(20230224)

目录
1. 列表奇偶拆分 ★
2. 二叉树的后序遍历 ★★
3. 接雨水 ★★★
附录
二叉树
特点
性质
特殊二叉树
满二叉树
完全二叉树
完全二叉树性质
二叉树的遍历
1. 列表奇偶拆分
【问题描述】 输入一个列表,包含若干个整数(允许为空),然后将其中的奇数和偶数单独放置在一个列表中,保持原有顺序
【输入形式】
【输出形式】
分两行输出,第一行输出偶数序列,第二行输出奇数序列
【样例输入1】
[48,82,47,54,55,57,27,73,86,14]
【样例输出1】
48, 82, 54, 86, 14
47, 55, 57, 27, 73
【样例输入2】
[10, 22, 40] 【
样例输出2】
10, 22, 40
NONE
【样例说明】
如果奇偶拆分后,奇数列表,或者偶数列表为空,请直接输出NONE表示
【代码】
x = input()
x1 = x.strip('[]')
x2 = x1.split(",")
a = []
b = []
for i in x2:if int(i) % 2 == 0:a.append(i)else:b.append(i)
if a == []:print("NONE")
else:print(a)
if b == []:print("NONE")
else:print(b)输入输出:
48,82,47,54,55,57,27,73,86,14
['48', '82', '54', '86', '14']
['47', '55', '57', '27', '73']
==============================
10, 22, 40
['10', ' 22', ' 40']
NONE
2. 二叉树的后序遍历
给定一个二叉树,返回它的 后序 遍历。
示例:
输入: [1,null,2,3] 输出: [3,2,1] 进阶: 递归算法很简单,你可以通过迭代算法完成吗?
代码:
class TreeNode:def __init__(self, x):self.val = xself.left = Noneself.right = None
class Solution(object):def postorderTraversal(self, root: TreeNode):if root is None:return []stack, output = [], []stack.append(root)while stack:node = stack.pop()output.append(node.val)if node.left:stack.append(node.left)if node.right:stack.append(node.right)return output[::-1]输出:
[3, 2, 1]
另:两种递归的代码
class TreeNode:def __init__(self, x):self.val = xself.left = Noneself.right = Nonedef PostOrder(t):'''直接打印'''if t != None:PostOrder(t.left)PostOrder(t.right)print(t.val, end = ' ')def PostOrderList(t):'''返回列表'''res = []if t != None:res.extend(PostOrderList(t.left))res.extend(PostOrderList(t.right))res.append(t.val)return resif __name__ == '__main__':t = TreeNode(1)t.right = TreeNode(2)t.right.left = TreeNode(3)PostOrder(t)print()print(PostOrderList(t))3. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5] 输出:9
提示:
n == height.length0 <= n <= 3 * 1040 <= height[i] <= 105
代码:
class Solution(object):def trap(self, height):ls = len(height)if ls == 0:return 0res, left = 0, 0while left < ls and height[left] == 0:left += 1pos = left + 1while pos < ls:if height[pos] >= height[left]:res += self.rain_water(height, left, pos)left = pospos += 1elif pos == ls - 1:max_value, max_index = 0, posfor index in range(left + 1, ls):if height[index] > max_value:max_value = height[index]max_index = indexres += self.rain_water(height, left, max_index)left = max_indexpos = left + 1else:pos += 1return resdef rain_water(self, height, start, end):if end - start <= 1:return 0min_m = min(height[start], height[end])res = min_m * (end - start - 1)step = 0for index in range(start + 1, end):if height[index] > 0:step += height[index]return res - stepif __name__ == '__main__':s = Solution()print (s.trap([2,6,3,8,2,7,2,5,0]))print (s.trap([0,1,0,2,1,0,1,3,2,1,2,1]))print (s.trap([4,2,0,3,2,5]))
输出:
11
6
9
附录
二叉树
二叉树(Binary Tree)是一种特殊的有序树型结构。
特点
(1)每个节点至多有两棵子树;
(2)二叉树的子树有左右之分;
(3)子树的次序不能任意颠倒(有序树)。
性质
(1)在二叉树的第i层上至多有2^(i-1)个节点(i>=1);
(2)深度为k的二叉树至多有2^k-1个节点(k>=1);
(3)对任何一棵二叉树,如果其叶子节点数为N0,度为2的结点数为N2,则N0=N2+1。
特殊二叉树
满二叉树
所有层的节点都达到最大数量,叶子除外的所有节点都有两个子节点,所有叶子都在最底一层(k)且数目为2^(k - 1)。即深度k且有2^k - 1个节点(叶子“长”满最后一层),或称完美二叉树 (Perfect Binary Tree)
完全二叉树
如果删除最底一层的所有叶子它就是满二叉树,即除了最后一层,每层节点都达到最大数量 ,即有深度k的个节点数在左闭右开【2^(k-1)+1,2^k-1】区间内。(Complete Binary Tree)
完全二叉树性质
1. 具有N个节点的完全二叉树的深度为[log2 N]+1,其中[x]为高斯函数,截尾取整。
2. 如果对一棵有n个节点的完全二叉树的节点按层序编号(从第一层到最后一层,每层从左到右),则对任一节点,有:
(1)如果i=1,则节点i是二叉树的根,无双亲;如果i>1,则其双亲节点为[i/2];
(2)如果2i>n,则节点i无左孩子;否则其左孩子是节点2i;
(3)如果2i+1>n,则节点i无右孩子;否则其右孩子是节点2i+1。
二叉树的遍历
指如何按某种搜索路径巡防树中的每个结点,使得每个结点均被访问一次,而且仅被访问一次。
常见的遍历方法有:先序、中序、后序遍历,一般都使用递归算法来实现。
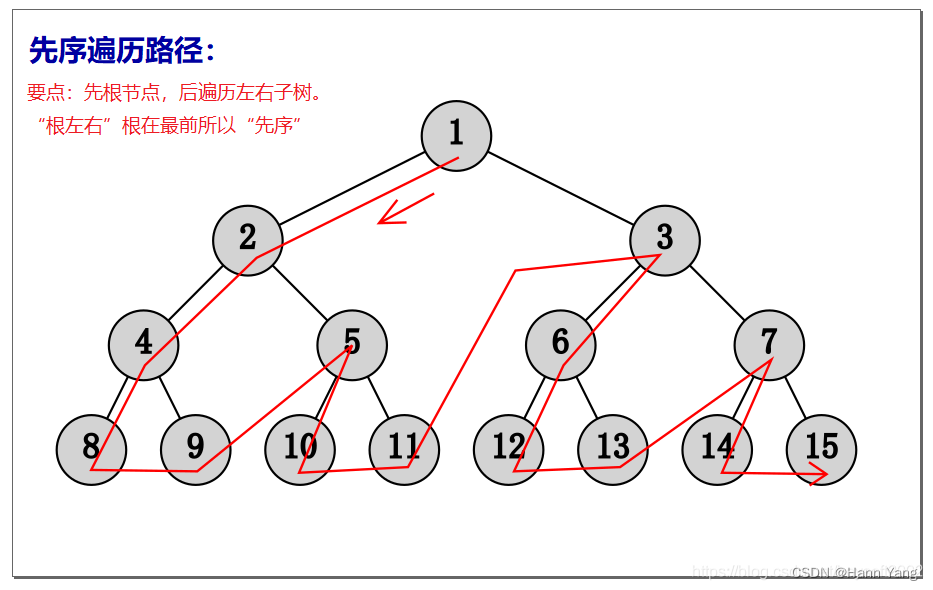
先序遍历
若二叉树为空,为空操作;
否则(1)访问根节点;(2)先序遍历左子树;(3)先序遍历右子树。
遍历结果: 1 [2 [4 8 9] [5 10 11]] [3 [6 12 13] [7 14 15] “根左右”
中序遍历
若二叉树为空,为空操作;
否则(1)中序遍历左子树;(2)访问根结点;(3)中序遍历右子树。
遍历结果: [[8 4 9] 2 [10 5 11]] 1 [[12 6 13] 3 [14 7 15]] “左根右”

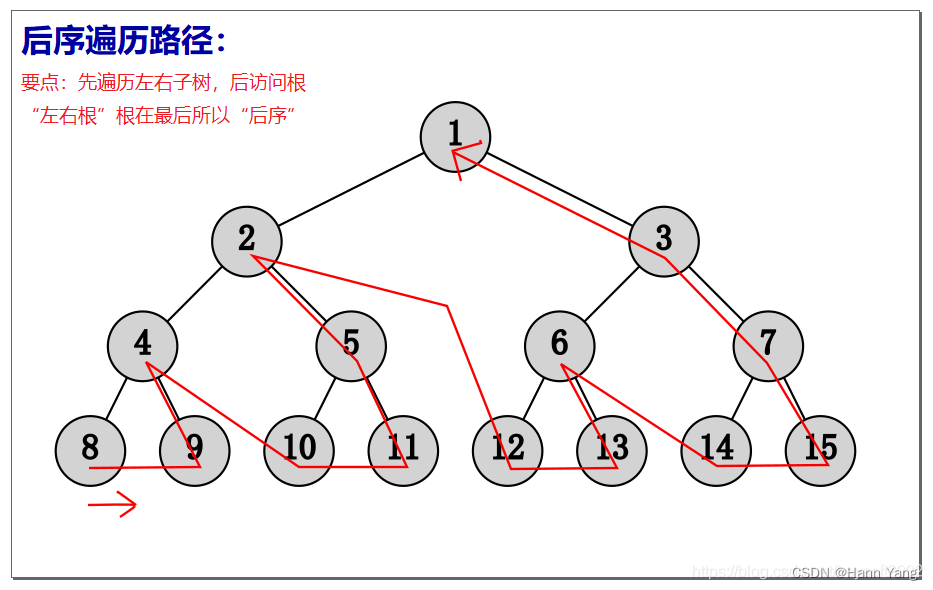
后序遍历
若二叉树为空,为空操作;
否则(1)后序遍历左子树;(2)后序遍历右子树;(3)访问根结点。
遍历结果: [[8 9 4] [10 11 5] 2] [[12 13 6] [14 15 7] 3] 1 “左右根”
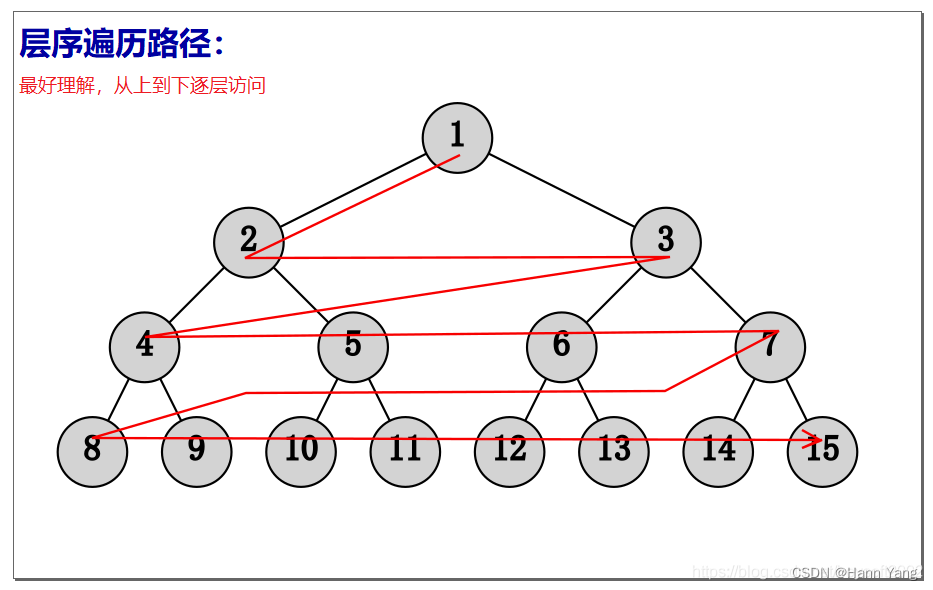
层序遍历
若二叉树为空,为空操作;否则从上到下、从左到右按层次进行访问。
遍历结果: 1 [2 3] [4 5 6 7] [8 9 10 11 12 13 14 15]
————————————————
End
相关文章:

Python每日一练(20230224)
目录 1. 列表奇偶拆分 ★ 2. 二叉树的后序遍历 ★★ 3. 接雨水 ★★★ 附录 二叉树 特点 性质 特殊二叉树 满二叉树 完全二叉树 完全二叉树性质 二叉树的遍历 1. 列表奇偶拆分 【问题描述】 输入一个列表,包含若干个整数(允许为空ÿ…...
【Linux】-- Shell的运行原理、Linux当中的权限
目录 Shell的运行原理 Linux权限的概念 su命令 权限 文件访问权限的相关设置方法 chmod指令 chown指令 chgrp指令 sudo命令 文件的常见问题 umask 粘滞位 关于权限的总结 Shell的运行原理 Shell运行原理 —— 外壳程序。 Linux严格意义上说的是一个操作系统&…...
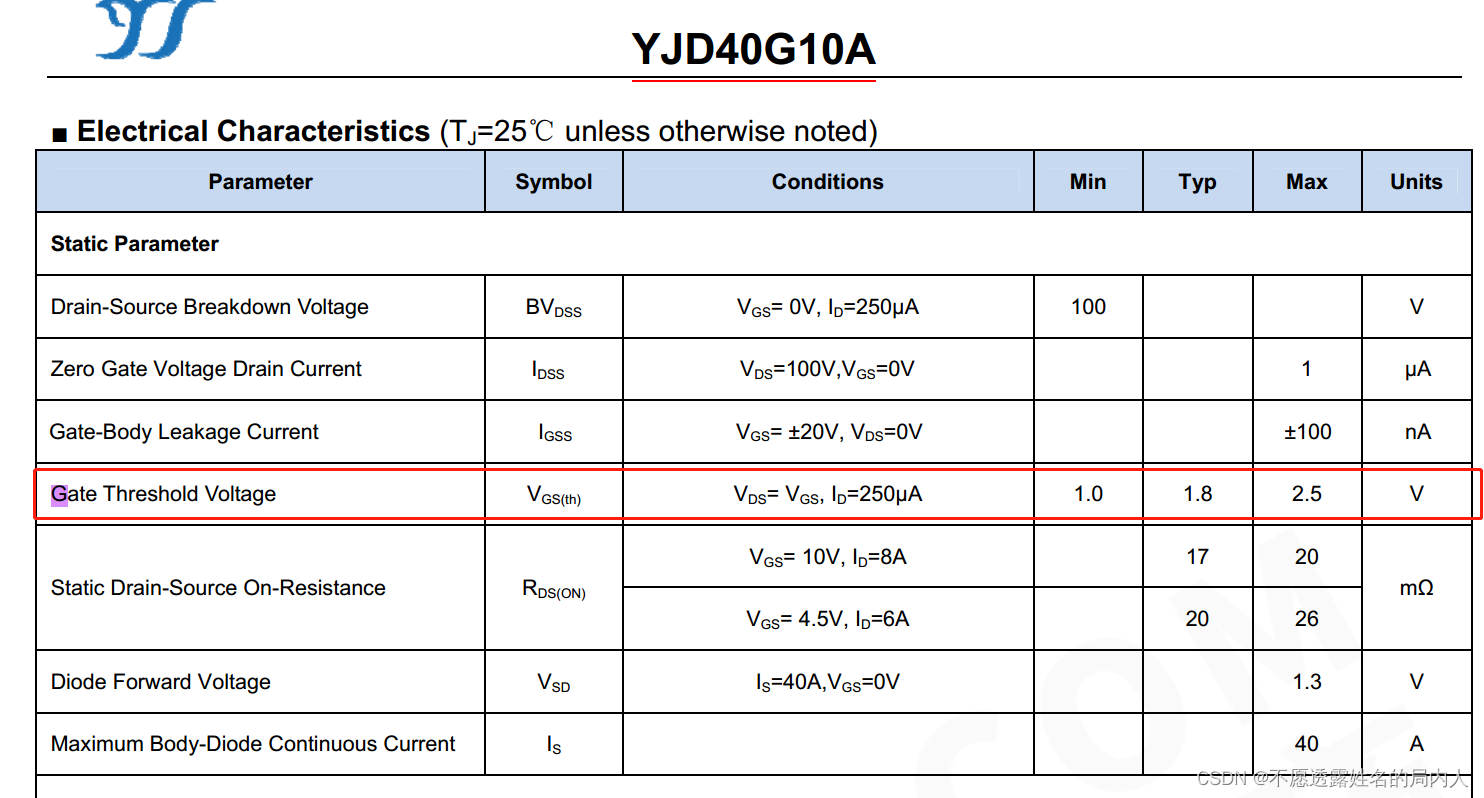
MOS管选型参数:VGS(th)
MOS管选型参数:VGS(th) VGS(th):开启电压(阀值电压)。当外加栅极控制电压 VGS 超过 VGS(th) 时,漏区和源区的表面反型层形成了连接的沟道。应用中,常将漏极短…...
二.线性表之顺序表
文章目录前言一.顺序表的概念及结构二.顺序表的接口实现1.顺序表的动态存储2.顺序表的初始化3.顺序表尾插#封装:扩容函数4.顺序表尾删5.顺序表头插6.顺序表头删7.顺序表查找8.顺序表在pos位置插入x9.顺序表删除pos位置的值10.顺序表销毁11.顺序表打印三.源1.Seqlist…...

ElasticSearch - SpringBoot整合ElasticSearch实现文档的增删改
文章目录1. ElasticSearch和kibana的安装和配置2. SpringBoot 项目环境搭建3. 创建索引4. 索引文档5. 更新文档6. 删除文档https://www.elastic.co/guide/en/elasticsearch/reference/current/search-your-data.htmlhttps://www.elastic.co/guide/cn/elasticsearch/guide/curre…...

JavaScript 库
文章目录JavaScript 库JavaScript 框架(库)jQueryPrototypeMooTools其他框架CDN -内容分发网络引用 jQuery使用框架JavaScript 库 JavaScript 库 - jQuery、Prototype、MooTools。 JavaScript 框架(库) JavaScript 高级程序设计…...

云解析DNS为什么要配置默认线路?
传统解析技术不会判断访客IP,而是会随机选择一个IP返回给访问者,这样就有可能造成移动用户访问电信服务器IP,北京用户访问深圳服务器IP这种跨域跨网访问的情况,产生非常大的延迟,带来很不好的访问体验。 而云解析DNS会…...
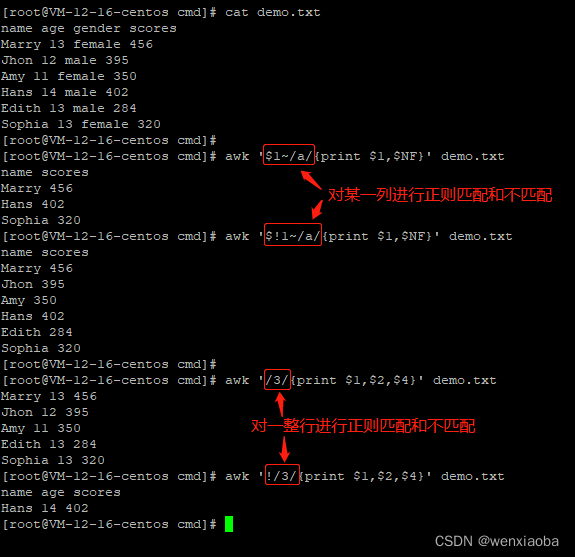
Linux命令之awk
awk是一个有强大的文本格式化能力的linux命令,早期是在Unix上实现的,linux后来也可以使用了,我们在Linux上使用的awk是gawk(GNU awk的意思) 语法 awk [option] 模式{动作} file option表示awk的可选参数,可…...
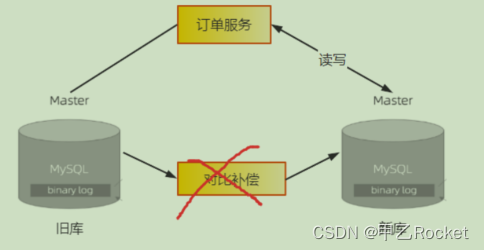
实战-缓存数据一致+binlog初始+cannel监听+数据迁移,数据一致性架构设计
前言 一. 解决缓存不命中(高并发操作击穿打挂DB的风险) 当并发量打的时候,当我们的缓存过期时,就算到数据库的比例偏小的时候,我们的请求时比较大的。那也会存在数据库崩掉的情况。解决方案想法如下(总体…...

nginx配置中proxy_pass反向代理502的bug
记录一个坑人的bug, 我今天在一台新的liunx上运行nginx来进行反向代理时候,发现怎么测都是502 我把配置全部删了从头开始配置,发现80端口正常,80端口index.html正常,反向代理转向http://127.0.0.1/也正常,…...
JavaScript 两种方案打开文件对话框
JavaScript 两种方案打开文件对话框 文章目录JavaScript 两种方案打开文件对话框一、文件对话框二、传统方案表单元素🌈三、文件系统访问API💦四、更进一步使用六、代码仓库🌐七、参考资料💘七、推荐博文🍗一、文件对话…...
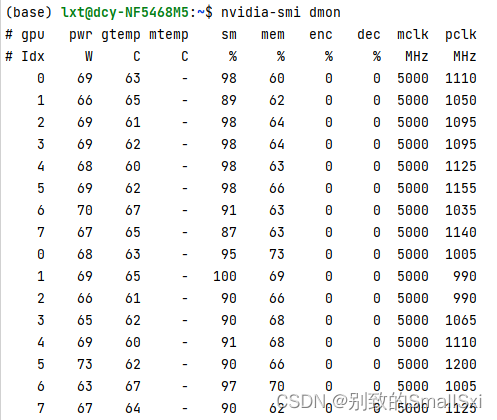
Pycharm远程服务器常见问题
2023年02月23日 问题描述:Pycharm远程服务器跑代码时,不小心把Pycharm关掉了,但服务器代码还在运行? 解决办法:kill进程 先用watch -n 0.5 nvidia_smi查看进程,然后kill -9 <进程> 1、nvidia-smi…...
内容团队如何快速出稿
对于内容团队而言,每个内容选题就相当于一个小项目,它们并非简单的线性工作流,相反其复杂程度不亚于一个小型工厂。一个内容选题会涉及内容形式,选题类型等多个变量,这些变量因素组合起来就是十几种不同类型的工作流。…...

es-08索引的批量操作
索引的批量操作 批量查询和批量增删改 批量查询 GET /_mget#批量查询 GET product/_search GET /_mget {"docs": [{"_index": "product","_id": 2},{"_index": "product","_id": 3}] }GET product/_mge…...
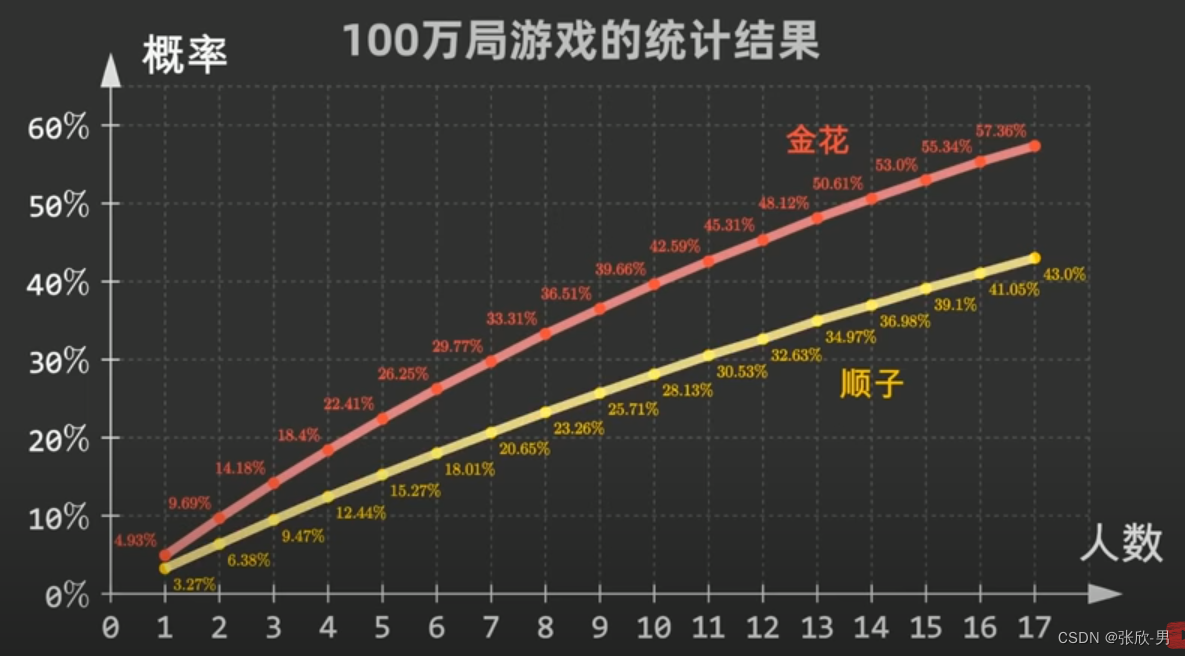
诈金花的概率
游戏使用一副除去大小王的扑克牌,共4个花色52张牌。 1、豹子(AAA最大,222最小)。2、同花顺(AKQ最大,A23最小)。3、同花(AKQ最大,352最小)。4、顺子ÿ…...

ESP32设备驱动-MLX90393磁场传感器驱动
MLX90393磁场传感器驱动 文章目录 MLX90393磁场传感器驱动1、MLX90393介绍2、硬件准备3、软件准备4、驱动实现1、MLX90393介绍 MLX90393 磁场传感器可以在运行时重新编程为不同的模式和不同的设置。 该传感器使用 Melexis 专有的 Triaxis 技术提供与沿 XYZ 轴感应的磁通密度成…...
Java面试题-Spring框架
Spring框架 1. BeanFactory和ApplicationContext有何区别 BeanFactory是Spring最底层的接口,是IoC的核心,定义IoC的基本功能。 BeanFactory具有:延迟实例化的特性。在启动的时候,不会实例化Bean,只有有需要从容器…...

【计算机物理模拟】-力矩、转动惯量和角速度之间的关系
力矩和角速度之间的关系可以通过牛顿第二定律和角动量定理来描述。 牛顿第二定律表明,物体的加速度与作用在物体上的合力成正比,加速度的方向与合力的方向相同。而对于旋转运动的物体,其加速度可以表示为半径 rrr 乘以角加速度 α\alphaα&a…...

async和await用法理解和快速上手 , 同步任务和异步任务顺序安排和轻松理解 , js代码执行顺序表面知道
学习关键语句 : async , await 用法 await 怎么使用 同步任务和异步任务 微任务和宏任务 js中代码执行顺序 写在前面 虽然说 async 和 await 是 Promise 的语法糖 , 但是用惯了Promise 的人(我) , 还真不能超快速使用上这个语法糖 , 所以赶紧写一篇文章出来让各位了解了解这个…...
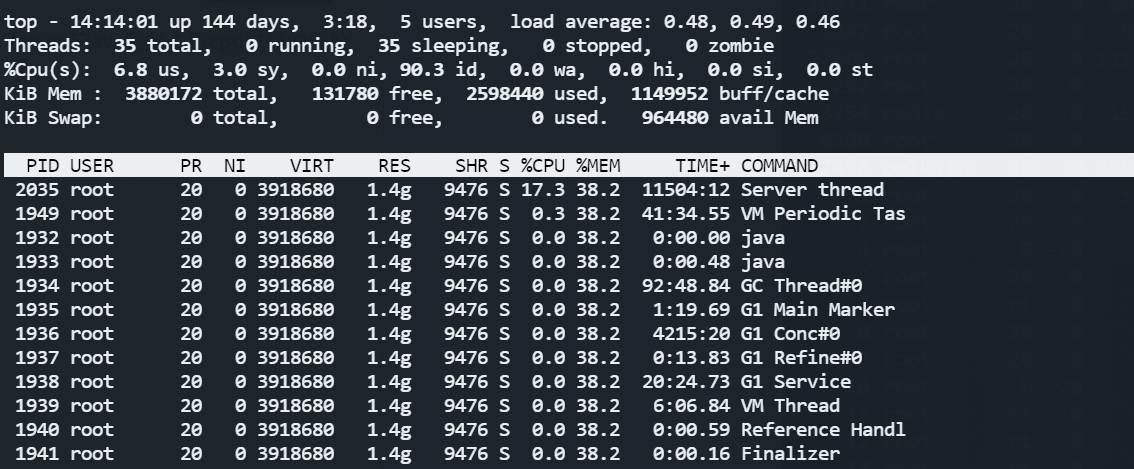
Linux下java服务占用cpu过高如何处理
Linux下java服务占用cpu过高如何处理 top命令查看进程信息 top按下shiftp,按cpu使用率排行,可见进程1932占用最高,并且是一个java服务 使用jps命令确认java服务 [rootVM-16-16-centos ~]# jps 1011 Jps 9462 yuan_back-0.0.1-SNAPSHOT.jar 1932 spigot-1.18.jar查找异常进程中…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
