VP记录——The 2021 CCPC Weihai Onsite
网址
2021CCPC威海
赛时过题与罚时

A.Goodbye, Ziyin!
签到题,队友写的
#include<bits/stdc++.h>
using namespace std;
int cnt[10], de[1000010];
int main() {int n;cin >> n;for(int i = 1; i < n; ++i) {int u, v;scanf("%d %d", &u, &v);++de[u];++de[v];}for(int i = 1; i <= n; ++i) {if(de[i] > 3) {cout << "0";return 0;}cnt[de[i]]++;}cout << cnt[1] + cnt[2];return 0;
}
D.Period
队友写的KMP,签到题
#include <bits/stdc++.h>
using namespace std;
#define MAXN 1000005
char s[MAXN];
int nxt[MAXN];
int n;
int ans[MAXN];
int main()
{scanf("%s", s + 1);n = strlen(s + 1);int j = 0;for(int i = 2; i <= n; ++i){while(j && s[i] != s[j + 1]) j = nxt[j];if(s[i] == s[j + 1]) j++;nxt[i] = j;}/* for(int i = 1; i <= n; ++i)* {* cout << nxt[i] << " ";* }* cout << "\n"; */j = nxt[n];while(j){int l = j;int r = n - l + 1;if(r > l){ans[r] --;ans[l + 1] ++;}j = nxt[j];}for(int i = 1; i <= n; ++i)ans[i] = ans[i] + ans[i-1];/* for(int i = 1; i <= n; ++i)* {* cout << ans[i] << " ";* }* cout << "\n"; */int q;scanf("%d", &q);while(q--){int l;scanf("%d", &l);printf("%d\n", ans[l]);}return 0;
}
G. Shinyruo and KFC
简单组合计数
若 k < m a x ( a i ) k<max(a_i) k<max(ai),显然无解
有解时答案是 ∏ i = 1 n C ( k , a i ) = ∏ i = 1 n k ! a i ! ∗ ( k − a i ) ! \prod_{i=1}^{n} C(k,a_i)=\prod_{i=1}^{n} \frac{k!}{{a_i}!*(k-a_i)!} ∏i=1nC(k,ai)=∏i=1nai!∗(k−ai)!k!
这样显然有一个 O ( m n ) O(mn) O(mn)的做法
观察数据性质 ∑ i = 1 n a i < = 1 e 5 \sum_{i=1}^{n}a_i<=1e5 ∑i=1nai<=1e5
即 a i a_i ai的种类数量级别为 s q r t ( n ) sqrt(n) sqrt(n)
那么就可以把相同的 a i a_i ai一起做,优化成 O ( m n ) O(m\sqrt{n}) O(mn)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5+5;
const int MOD = 998244353;
int n, m, a[N];
ll b[N];
ll c[N];
ll cnt[N];
ll power(ll x, ll y) {if(y == 0) {return 1;}ll res = 1;while(y){if(y&1) res = res * x % MOD;x = x * x % MOD; y >>= 1;}return res;
}
ll ni(ll x) {return power(x, MOD - 2);
}
int main() {scanf("%d %d", &n, &m);b[0] = 1;for(ll i = 1; i <= 1e5; ++i) {b[i] = b[i - 1] * i % MOD;c[i] = power(b[i], n);}int mx = 0;for(ll i = 1; i <= n; ++i ) {scanf("%d", &a[i]);++cnt[a[i]];mx = max(mx, a[i]);}sort(a + 1, a + 1 + n);n = unique(a + 1, a + 1 + n) - (a + 1);for(int k = 1; k <= m; ++k) {if(k < mx) {puts("0");continue;}ll ans = c[k];for(ll i = 1; i <= n; ++i) {ll t = b[a[i]] * b[k - a[i]] % MOD;t = power(t, cnt[a[i]]);ans = ans * ni(t) % MOD;}printf("%lld\n", ans);}return 0;
}
H. city safet
发现 n n n的范围很像网络流,然后就往这方面想,后面发现每当多选择一个距离相当于是获得了 v i + 1 − v i v_{i+1}-v_{i} vi+1−vi的贡献,每当修复了一个点,相当于是花费了 w i w_i wi,我们要统一边权的性质,即我们可以想办法把问题变成最大贡献或者最小花费
那么我们可以假设初始时全部修复,
那么每个点建立 n n n个代表点, i d i , j id_{i,j} idi,j表示以点 i i i为中心,距离 < = j <=j <=j的一类点,共 n ∗ n n*n n∗n个代表点
然后建立 n n n个具体点 1 1 1到 n n n
对于建图而言,
第 i i i个点的代表点 j j j向代表点 j − 1 j-1 j−1连边, ( i , j ) − > ( i , j − 1 ) (i,j)->(i,j-1) (i,j)−>(i,j−1),边权为 v j − v j − 1 v_{j}-v_{j-1} vj−vj−1,可理解成是反悔边,反悔这次距离的添加
每个代表点 ( i , j ) (i,j) (i,j)连向所有跟 i i i距离为 j j j的具体点, ( i , j ) − > k 当 d i s [ i ] [ k ] = j (i,j)->k 当dis[i][k]=j (i,j)−>k当dis[i][k]=j,边权为无穷
源点向所有代表点连边,边权为无穷, S − > ( i , j ) S->(i,j) S−>(i,j)
所有具体点向汇点连边,边权为对应的 w i w_i wi, i − > T i->T i−>T,因为一个点最坏情况就是直接修了它
那么最小花费就是求最小割,直接网络流即可
那么答案就是 n ∗ v n − m a x f l o w n*v_n-maxflow n∗vn−maxflow
#include<bits/stdc++.h>
#define INF 0x7fffffff
using namespace std;const int N = 205;
const int M = 4e5+5;struct node {int to, next, w;
}e[M];
int n, m, k = 1, head[M], d[M];
int id[N][N], w[N], v[N];
int f[N][N];
int S, T, Maxflow, Num;void build(int u, int v, int w) {e[++k] = (node) {v, head[u], w};head[u] = k;e[++k] = (node) {u, head[v], 0};head[v] = k;
}queue<int> q;bool bfs() {while(!q.empty()) q.pop();for(int i = S; i <= T; ++i) d[i] = 0;d[S] = 1;q.push(S);while(!q.empty()) {int u = q.front();q.pop();for(int i = head[u]; i; i = e[i].next){int v = e[i].to;if(e[i].w && !d[v]) {d[v] = d[u] + 1;q.push(v);if(v == T) return 1;}}}return 0;
}
int dfs(int dep, int flow) {if(dep == T) {return flow;}int rest = flow, rp = 0;for(int i = head[dep]; i && rest; i = e[i].next) {int v = e[i].to;if(d[v] == d[dep] + 1 && e[i].w) {rp = dfs(v, min(e[i].w, rest));if(!rp) {d[v] = 0;}e[i].w -= rp;e[i ^ 1].w += rp;rest -= rp;}}return flow - rest;
}
void dinic() {int flow;while(bfs()) {while(flow = dfs(S, INF)) {Maxflow += flow;}}
}int main() {scanf("%d", &n);S = 0;T = n*n+n+1;for (int i = 1; i <= n; i++) scanf("%d", &w[i]);for (int i = 1; i <= n; i++) scanf("%d", &v[i]); int U, V;memset(f, 0x3f, sizeof(f));for (int i = 1; i < n; i++) {scanf("%d%d", &U, &V);if (U != V) f[U][V] = f[V][U] = 1;}for (int i = 1; i <= n; i++) build(i, T, w[i]);Num = n;for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++) id[i][j] = ++Num;for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {build(S, id[i][j], v[j]-v[j-1]);build(id[i][j], id[i][j-1], INF); }} for (int i = 1; i <= n; i++) f[i][i] = 0;for (int k = 1; k <= n; k++)for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++) f[i][j] = min(f[i][j], f[i][k] + f[k][j]);for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) {build(id[i][f[i][j]+1], j, INF); }dinic();printf("%d\n", n*v[n]-Maxflow);return 0;
}
J.Circular Billiard Table
签到题,我写的,题意是给一个入射角,求在圆内最少弹射多少次能回到原点
入射角是 a b \frac{a}{b} ba,那么假设有 x x x个转角,要弹 y y y圈
显然有 a b ∗ x ∗ 2 = 360 ∗ y \frac{a}{b}*x*2=360*y ba∗x∗2=360∗y
构造 x = 180 ∗ b , y = a x=180*b,y=a x=180∗b,y=a然后除 g c d gcd gcd就可以了
#include<bits/stdc++.h>using namespace std;typedef long long ll;ll gcd(ll a, ll b) {return (!b) ? a : gcd(b, a%b);
}
ll t, a, b;int main() {scanf("%lld", &t);while (t--) {scanf("%lld%lld", &a, &b);long long A = 180*b, B = a;ll c = gcd(A, B);ll ans = A/c-1;printf("%lld\n", ans);}return 0;
}
M.810975
题意是构造一个长度为 n n n的01串,其中有 m m m个1,最长连续1 等于 k k k,问总方案数
相当于是在0的 n − m + 1 n-m+1 n−m+1个空隙里面插入1
容斥一下,
答案即为
n − m + 1 n-m+1 n−m+1个数中,满足 0 < = x i < = k 0<=x_i<=k 0<=xi<=k且 ( ∑ i = 1 n − m + 1 x i ) = m (\sum_{i=1}^{n-m+1}x_i)=m (∑i=1n−m+1xi)=m的方案数
减去
n − m + 1 n-m+1 n−m+1个数,满足 0 < = x i < = k − 1 0<=x_i<=k-1 0<=xi<=k−1且 ( ∑ i = 1 n − m + 1 x i ) = m (\sum_{i=1}^{n-m+1}x_i)=m (∑i=1n−m+1xi)=m的方案数
经典问题,队友直接秒了!
#include <bits/stdc++.h>
using namespace std;
#define mo 998244353
#define maxn 1000005
#define MAXN 1000005
#define ll long long
namespace Poly
{inline void Add(int &x,int y){x+=y;x-=(x>=mo?mo:0);}inline int add(int x,int y){x+=y;return x>=mo?x-mo:x;}int A[maxn],B[maxn],C[maxn],D[maxn],E[maxn],inv[maxn],R[maxn],len,sz,ny;inline int ksm(int x,int y=mo-2){int a=1;if(y<0)y+=mo-1;while(y){if(y&1)a=1ll*a*x%mo;x=1ll*x*x%mo;y>>=1;}return a;}inline void init(int n){int i;inv[1]=1;for(i=2;i<=n;++i)inv[i]=1ll*(mo-mo/i)*inv[mo%i]%mo;}inline void Inte(int *a,int n){for(int i=n-1;i>=1;--i)a[i]=1ll*a[i-1]*inv[i]%mo;a[0]=0;}inline void Deri(int *a,int n){for(int i=1;i<n;++i)a[i-1]=1ll*a[i]*i%mo;a[n-1]=0;}inline void pre(int n){len=1,sz=-1;while(len<n)len<<=1,++sz;ny=ksm(len);for(int i=1;i<len;++i)R[i]=(R[i>>1]>>1)|((i&1)<<sz);}inline void NTT(int *a,int fl)//fl==1?3:332748118;{int i,j,k,t,y,p,w,wn;for(i=1;i<len;++i)if(i<R[i])swap(a[i],a[R[i]]);for(i=2,p=1;i<=len;p=i,i<<=1)for(wn=ksm(fl,(mo-1)/i),j=0;j<len;j+=i)for(w=1,k=0;k<p;++k,w=1ll*w*wn%mo){t=a[j|k],y=1ll*w*a[j|k|p]%mo;a[j|k]=add(t,y),a[j|k|p]=add(t,mo-y);}}inline void Mul(int *a,int *b,int *c,int nm,int n,int m)//a is the ans;{if(!n||!m){fill(a,a+nm,0);return ;}pre(n+m-1);for(int i=0;i<n;++i)A[i]=b[i];fill(A+n,A+len,0);for(int i=0;i<m;++i)B[i]=c[i];fill(B+m,B+len,0);NTT(A,3);NTT(B,3);for(int i=0;i<len;++i)A[i]=1ll*A[i]*B[i]%mo;NTT(A,332748118);for(int i=0;i<nm;++i)a[i]=1ll*A[i]*ny%mo;}inline void Inv(int *a,int *b,int n)//this n include zero position;{if(n==1)return a[0]=ksm(b[0]),void();int m=(n+1)>>1,i;Inv(a,b,m);pre(n<<1);for(i=0;i<m;++i)A[i]=a[i];fill(A+m,A+len,0);for(i=0;i<n;++i)B[i]=b[i];fill(B+n,B+len,0);NTT(A,3);NTT(B,3);for(i=0;i<len;++i)A[i]=1ll*A[i]*add(2,mo-1ll*A[i]*B[i]%mo)%mo;NTT(A,332748118);for(i=0;i<n;++i)a[i]=1ll*A[i]*ny%mo;}inline void Ln(int *a,int *b,int n)//a is the ans;b[0]need equal 1;{Inv(a,b,n);int i;pre(n<<1);for(i=0;i<n;++i)C[i]=b[i];Deri(C,n);for(i=0;i<n;++i)A[i]=a[i];fill(A+n,A+len,0);for(i=0;i<n;++i)B[i]=C[i];fill(B+n,B+len,0);NTT(A,3);NTT(B,3);for(i=0;i<len;++i)A[i]=1ll*A[i]*B[i]%mo;NTT(A,332748118);for(i=0;i<n;++i)a[i]=1ll*A[i]*ny%mo;Inte(a,n);}inline void Exp(int *a,int *b,int n)//a is the ans;{if(n==1)return a[0]=1,void();int m=(n+1)>>1,i;Exp(a,b,m);Ln(D,a,n);pre(n<<1);for(i=0;i<m;++i)A[i]=a[i];fill(A+m,A+len,0);for(i=0;i<n;++i)B[i]=add(b[i],mo-D[i]);++B[0];fill(B+n,B+len,0);NTT(A,3);NTT(B,3);for(i=0;i<len;++i)A[i]=1ll*A[i]*B[i]%mo;NTT(A,332748118);for(i=0;i<n;++i)a[i]=1ll*A[i]*ny%mo;}inline void Ksm(int *a,int *b,int n, ll k)//a b should be differented;a is the ans;b[0] need equal 1;{Ln(E,b,n);k%=mo;for(int i=0;i<n;++i)E[i]=1ll*E[i]*k%mo;Exp(a,E,n);}
}
int n, m, k;
int a[MAXN];
int b[MAXN];
int main()
{cin >> n >> m >> k;if(n == 0){if(m == 0 && k == 0) { cout << 1 << "\n"; return 0; }else { cout << 0 << "\n"; return 0; }}if(n < m) { cout << 0 << "\n"; return 0;}if(m < k) { cout << 0 << "\n"; return 0; }if(m == 0){if(k == 0) { cout << 1 << "\n"; return 0;}else { cout << 0 << "\n"; return 0;}}if(k == 0){if(m == 0) { cout << 1 << "\n"; return 0;}else { cout << 0 << "\n"; return 0; }}n = n - m + 1;Poly::init(800000);memset(a, 0, sizeof a);for(int i = 0; i <= k; ++i) a[i] = 1;Poly::Ksm(b, a, m + 1, n);int ans = b[m];memset(a, 0, sizeof a);for(int i = 0; i < k; ++i) a[i] = 1;memset(b, 0, sizeof b);Poly::Ksm(b, a, m + 1, n);ans = (ans - b[m] + mo) % mo;cout << ans << "\n";return 0;
}
相关文章:

VP记录——The 2021 CCPC Weihai Onsite
网址 2021CCPC威海 赛时过题与罚时 A.Goodbye, Ziyin! 签到题,队友写的 #include<bits/stdc.h> using namespace std; int cnt[10], de[1000010]; int main() {int n;cin >> n;for(int i 1; i < n; i) {int u, v;scanf("%d %d", &…...
JavaWeb---Servlet
1.Srvlet概述 Servlet是运行在java服务器端的程序,用于接收和响应来着客户端基于HTTP协议的请求 如果想实现Servlet的功能,可以通过实现javax。servlet。Servlet接口或者继承它的实现类 核心方法:service()…...
英语——方法篇——单词——谐音法+拼音法——50个单词记忆
theatre,剧场,太后th吃eat热re食物,就去剧场了 loud dolphin,做do脸皮厚plh在。。。里 humid,hu湖mi米d的 blender,b爸lend借给er儿。 tragedy,tr土人...

35道Rust面试题
这套Rust面试题包括了填空题、判断题、连线题和编码题等题型。 选择题 1 ,下面哪个是打印变量language的正确方法? A,println("{}", language); B,println(language); C,println!("{}", langu…...
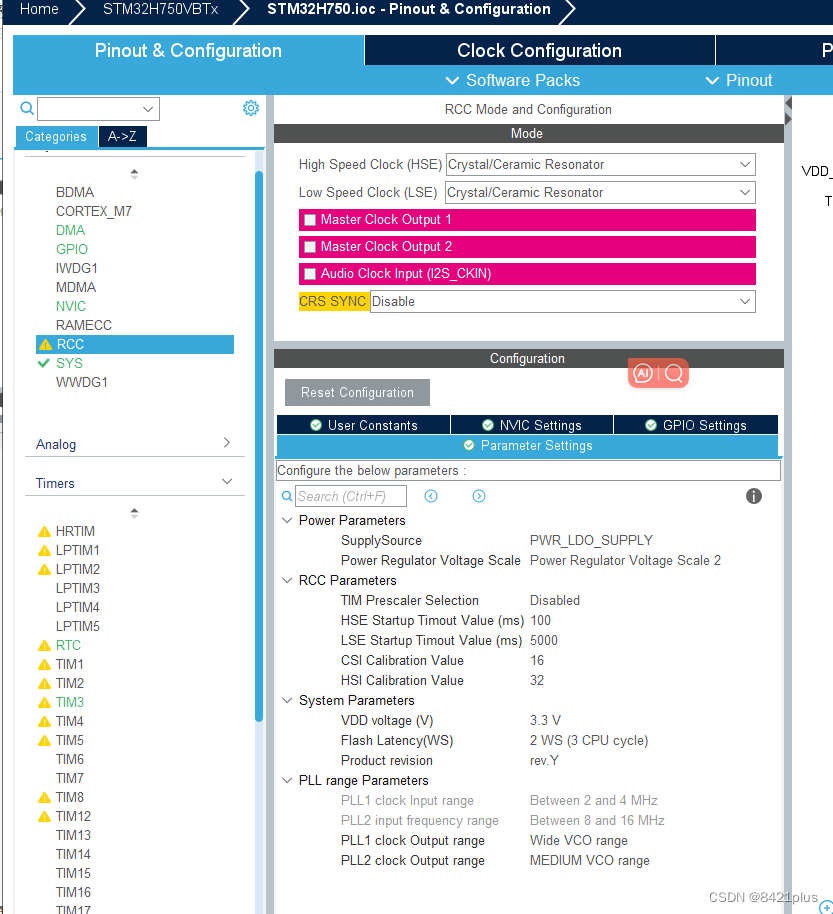
01 时钟配置初始化,debug
1. 开启debug series,否则只能下载一次,再次下载要配置boot 2.f0外部时钟配置 h750 配置 实测可用...

Halcon我的基础教程(一)(我的菜鸟教程笔记)-halcon仿射变换(Affine Transformation)的探究与学习
目录 什么是仿射变换?仿射变换有哪些方式?任何仿射变换都能由以下基本变换构造而来:在Halocn中,仿射变换具有重要的作用,那我们本文章重点讨论仿射变换基础性知识。 使用Halcon中的重要算子,仿射变换一般解决步骤,案例应用会在以后的文章中我们重点解答与讨论。 我们首先…...
c++视觉---中值滤波处理
中值滤波(Median Filter)是一种常用的非线性平滑滤波方法,用于去除图像中的噪声。它不像线性滤波(如均值滤波或高斯滤波)那样使用权重来计算平均值或加权平均值,而是选择滤波窗口内的像素值中的中间值作为输…...
Edge使用猴油脚本实战(实验室安全考试系统刷在线时长——网站永久自动刷新)
介绍 篡改猴 (Tampermonkey) 是拥有 超过 1000 万用户 的最流行的浏览器扩展之一。它允许用户自定义并增强您最喜爱的网页的功能。用户脚本是小型 JavaScript 程序,可用于向网页添加新功能或修改现有功能。使用 篡改猴,您可以轻松在任何网站上创建、管理…...

Vue 中 KeepAlive 内置缓存使用
KeepAlive 介绍及使用场景 KeepAlive 是 vue 中的内置组件,当多个组件动态切换时可以对实例状态进行缓存,用法如下 <router-view v-slot"{ Component }"><keep-alive><component :is"Component" /></keep-al…...
语言模型编码中/英文句子格式详解
文章目录 前言一、Bert的vocab.txt内容查看二、BERT模型转换方法(vocab.txt)三、vocab内容与模型转换对比四、中文编码总结 前言 最近一直在学习多模态大模型相关内容,特别是图像CV与语言LLM模型融合方法,如llama-1.5、blip、meta-transformer、glm等大…...
【Node.js】路由
基础使用 写法一: // server.js const http require(http); const fs require(fs); const route require(./route) http.createServer(function (req, res) {const myURL new URL(req.url, http://127.0.0.1)route(res, myURL.pathname)res.end() }).listen…...

matlab 2ask 4ask 信号调制
1 matlab 2ask close all clear all clcL =1000;Rb=2822400;%码元速率 Fs =Rb*8; Fc=Rb*30;%载波频率 Ld =L*Fs/Rb;%产生载波信号 t =0:1/Fs:L/Rb;carrier&...
Python利用jieba分词提取字符串中的省市区(字符串无规则)
目录 背景库(jieba)代码拓展结尾 背景 今天的需求就是在一串字符串中提取包含,省、市、区,该字符串不是一个正常的地址;,如下字符串 "安徽省、浙江省、江苏省、上海市,冷运标快首重1kg价格xx元,1.01kg(含)-5kg(不含)续重价…...

MuLogin防关联浏览器帮您一键实现Facebook账号多开
导言: 在当今数字化时代,社交媒体应用程序的普及程度越来越高。Facebook作为全球最大的社交媒体平台之一,拥有数十亿的用户。然而,对于一些用户来说,只拥有一个Facebook账号可能无法满足他们的需求。有时,…...

【C语言】每日一题(半月斩)——day4
目录 选择题 1、设变量已正确定义,以下不能统计出一行中输入字符个数(不包含回车符)的程序段是( ) 2、运行以下程序后,如果从键盘上输入 65 14<回车> ,则输出结果为( &…...
 每次ssh进)
Are you sure you want to continue connecting (yes/no) 每次ssh进
Lunix scp等命令不需要输入yes确认方法_scp不需要确认-CSDN博客 方法一:连接时加入StrictHostKeyCheckingno ssh -o StrictHostKeyCheckingno root192.168.1.100 方法二:修改/etc/ssh/ssh_config配置文件,添加: StrictHostKeyC…...

网络与信息系统安全设计规范
1、总则 1.1、目的 为规范XXXXX单位信息系统安全设计过程,确保整个信息安全管理体系在信息安全设计阶段符合国家相关标准和要求,特制订本规范。 1.2、范围 本规范适用于XXXXX单位在信息安全设计阶段的要求和规范管理。 1.3、职责 网络安全与信息化…...
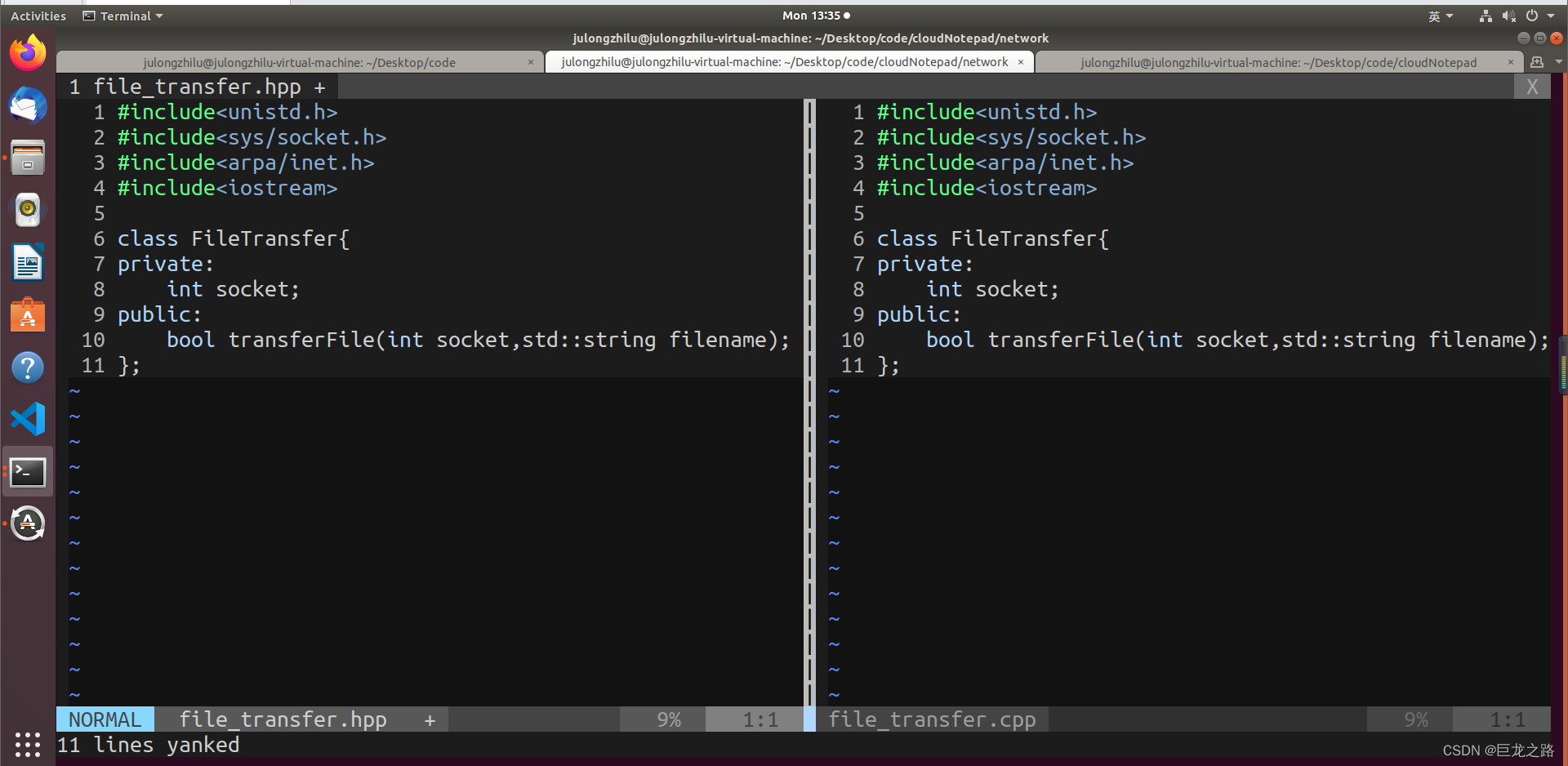
在Linux怎么用vim实现把一个文件里面的文本复制到另一个文件里面
2023年10月9日,周一下午 我昨天遇到了这个问题,但在网上没找到图文并茂的博客,于是我自己摸索出解决办法后,决定写一篇图文并茂的博客。 情景 假设现在我要用vim把file_transfer.cpp的内容复制到file_transfer.hpp里面 第一步 …...

CCAK—云审计知识证书学习
目录 一、CCAK云审计知识证书概述 二、云治理概述 三、云信任 四、构建云合规计划 <...
3.springcloudalibaba gateway项目搭建
文章目录 前言一、搭建gateway项目1.1 pom配置1.2 新增配置如下 二、新增server服务2.1 pom配置2.2新增测试接口如下 三、测试验证3.1 分别启动两个服务,查看nacos是否注册成功3.2 测试 总结 前言 前面已经完成了springcloudalibaba项目搭建,接下来搭建…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...
