【数据结构】二叉树的链式结构及实现
目录
1. 前置说明
2. 二叉树的遍历
2.1 前序、中序以及后序遍历
2.2 层序遍历
3. 节点个数及高度等
4. 二叉树的创建和销毁
1. 前置说明
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->_left = node2;node1->_right = node4;node2->_left = node3;node4->_left = node5;node4->_right = node6;return node1;
}注意:上述代码并不是创建二叉树的方式,真正创建二叉树方式后序详解重点讲解。
再看二叉树基本操作前,再回顾下二叉树的概念,二叉树是:
- 空树
- 非空:根节点,根节点的左子树、根节点的右子树组成的

从概念中可以看出,二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
2. 二叉树的遍历
2.1 前序、中序以及后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。

按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
// 二叉树前序遍历
void PrevOrder(BTNode* root);
// 二叉树中序遍历
void InOrder(BTNode* root);
// 二叉树后序遍历
void PostOrder(BTNode* root);void PrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->val);PrevOrder(root->left);PrevOrder(root->right);
}void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);
}下面主要分析前序递归遍历,中序与后序图解类似,大家可自己动手绘制。
前序遍历递归图解:


前序遍历结果:1 2 3 4 5 6
中序遍历结果:3 2 1 5 4 6
后序遍历结果:3 2 5 6 4 1
2.2 层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
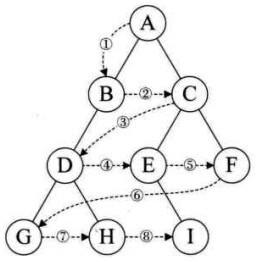
// 层序遍历
void LevelOrder(BTNode* root);void LevelOrder(BTNode* root)
{Que q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);printf("%d ", front->val);if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);QueuePop(&q);}printf("\n");QueueDestroy(&q);
}3. 节点个数及高度等
// 二叉树节点个数
int TreeSize(BTNode* root);
// 二叉树叶子节点个数
int TreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int TreeKLevel(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* TreeFind(BTNode* root, int x);
// 二叉树的高度
int TreeHeight(BTNode* root);int TreeSize(BTNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}int TreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}int TreeKLevel(BTNode* root, int k)
{assert(k > 0);if (root == NULL)return 0;if (k == 1)return 1;return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}BTNode* TreeFind(BTNode* root, int x)
{if (root == NULL)return NULL;if (root->val == x)return root;BTNode* ret = NULL;ret = TreeFind(root->left, x);if (ret)return ret;ret = TreeFind(root->right, x);if (ret)return ret;return NULL;
}int TreeHeight(BTNode* root)
{if (root == NULL)return 0;return fmax(TreeHeight(root->left), TreeHeight(root->right)) + 1;
}4. 二叉树的创建和销毁
// 手动构建二叉树
BTNode* BuyNode(int x);
// 二叉树销毁
void TreeDestroy(BTNode* root);
// 判断二叉树是否是完全二叉树
int TreeComplete(BTNode* root);BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");exit(-1);}node->val = x;node->left = NULL;node->right = NULL;return node;
}void TreeDestroy(BTNode* root)
{if (root == NULL)return;TreeDestroy(root->left);TreeDestroy(root->right);free(root);
}int TreeComplete(BTNode* root)
{Que q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);if (front == NULL)break;QueuePush(&q, front->left);QueuePush(&q, front->right);QueuePop(&q);}// 已经遇到空节点,如果队列中后面的节点还有非空,就不是完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front != NULL){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}本文完
相关文章:

【数据结构】二叉树的链式结构及实现
目录 1. 前置说明 2. 二叉树的遍历 2.1 前序、中序以及后序遍历 2.2 层序遍历 3. 节点个数及高度等 4. 二叉树的创建和销毁 1. 前置说明 在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构…...

OpenCV4(C++)—— 创建窗口滑动条来调参
文章目录 创建滑动条 —— createTrackbar 创建滑动条 —— createTrackbar createTrackbar是OpenCV中的一个函数,用于创建一个可调节的滑动条(Trackbar),以便在图像处理过程中实时调整参数 int cv::createTrackbar(const String…...
深度学习基础知识 学习率调度器的用法解析
深度学习基础知识 学习率调度器的用法解析 1、自定义学习率调度器**:**torch.optim.lr_scheduler.LambdaLR2、正儿八经的模型搭建流程以及学习率调度器的使用设置 1、自定义学习率调度器**:**torch.optim.lr_scheduler.LambdaLR 实验代码: i…...

【JUC系列-12】深入理解PriorityQueue的底层原理和基本使用
JUC系列整体栏目 内容链接地址【一】深入理解JMM内存模型的底层实现原理https://zhenghuisheng.blog.csdn.net/article/details/132400429【二】深入理解CAS底层原理和基本使用https://blog.csdn.net/zhenghuishengq/article/details/132478786【三】熟练掌握Atomic原子系列基本…...
Paddle安装
Paddle安装参考 docs/tutorials/INSTALL_cn.md PaddlePaddle/PaddleDetection - Gitee.comhttps://gitee.com/paddlepaddle/PaddleDetection/blob/release/2.6/docs/tutorials/INSTALL_cn.md # 不指定版本安装paddle-gpu python -m pip install paddlepaddle-gpu# 测试安装 …...
配置XP虚拟机和Win 10宿主机互相ping通
文章目录 一、关闭虚机和宿主机的防火墙1、关闭虚拟机的防火墙1.1方式一1.2方式二 2、关闭宿主机的防火墙 二、设置XP和宿主机VMnet8的IP地址、网关和DNS1、获取VMWare的虚拟网络配置信息2、设置XP的VMnet8的IP地址、网关和DNS3、设置宿主机VMnet8的IP地址、网关和DNS 三、获取…...
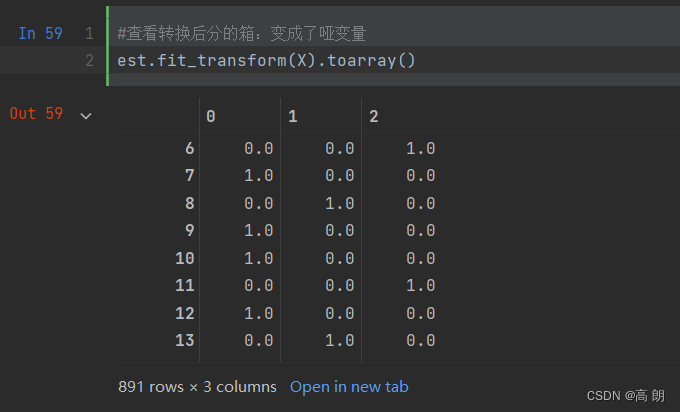
【机器学习】sklearn对数据预处理
文章目录 数据处理步骤观察数据数据无量纲化缺失值处理处理分类型特征处理连续型特征 数据处理步骤 数据无量纲化缺失值处理处理分类型特征:编码与哑变量处理连续型特征:二值化与分段 观察数据 通过pandas读取数据,通过head和info方法大致查…...

【智慧燃气】智慧燃气解决方案总体概述--终端层、网络层
关键词:智慧燃气、智慧燃气系统、智慧燃气平台、智慧燃气解决方案、智慧燃气应用、智能燃气 智慧燃气解决方案是基于物联网、大数据、云计算、移动互联网等先进技术,结合燃气行业特征,通过智能设备全面感知企业生产、环境、状态等信息的全方…...

Tomcat隔离web原理和热加载热部署
Tomcat 如何打破双亲委派机制 Tomcat 的自定义类加载器 WebAppClassLoader 打破了双亲委派机制,它首先自己尝试去加载某个类,如果找不到再代理给父类加载器,其目的是优先加载 Web 应用自己定义的类。具体实现就是重写 ClassLoader 的两个方法…...
使用ffmpeg和python脚本下载网络视频m3u8(全网最全面)
网上给娃找了些好看的电影和一些有趣的短视频,如何保存下来呢?从网上找各种工具?都不方便。于是想到何不编程搞定,搞个脚本。对程序员来说这都不是事儿。且我有华为云服务器,完全可以把地址记下,后台自动下…...
【考研408常用数据结构】C/C++实现代码汇总
文章目录 前言数组多维数组的原理、作用稀疏数组 链表单向链表的增删改查的具体实现思路约瑟夫环问题(可不学)双向链表 树二叉搜索树中序线索二叉树哈夫曼树的编码与译码红黑树B树B树 堆顺序与链式结构队列实现优先队列排序算法(重点…...

Flink学习笔记(二):Flink内存模型
文章目录 1、配置总内存2、JobManager 内存模型3、TaskManager 内存模型4、WebUI 展示内存5、Flink On YARN 模式下内存分配6、Flink On Yarn 集群消耗资源估算6.1、资源分配6.2、Flink 提交 Yarn 集群的相关命令6.3、Flink On Yarn 集群的资源计算公式 1、配置总内存 Flink J…...
信息系统项目管理师第四版学习笔记——项目绩效域
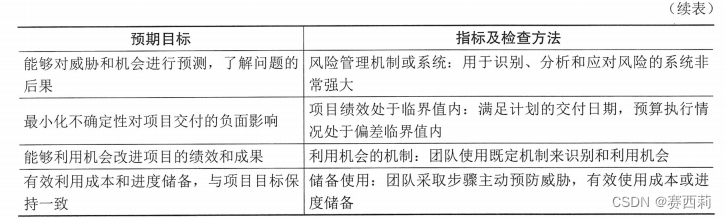
干系人绩效域 干系人绩效域涉及与干系人相关的活动和职能。在项目整个生命周期过程中,有效执行本绩效域可以实现的预期目标主要包含:①与干系人建立高效的工作关系;②干系人认同项目目标;③支持项目的干系人提高了满意度…...

PyTorch 深度学习之加载数据集Dataset and DataLoader(七)
1. Revision: Manual data feed 全部Batch:计算速度,性能有问题 1 个 :跨越鞍点 mini-Batch:均衡速度与性能 2. Terminology: Epoch, Batch-Size, Iteration DataLoader: batch_size2, sheffleTrue 3. How to define your Dataset 两种处…...

小谈设计模式(26)—中介者模式
小谈设计模式(26)—中介者模式 专栏介绍专栏地址专栏介绍 中介者模式分析角色分析抽象中介者(Mediator)具体中介者(ConcreteMediator)抽象同事类(Colleague)具体同事类(C…...

7种设计模式
1. 工厂模式 优点:封装了对象的创建过程,降低了耦合性,提供了灵活性和可扩展性。 缺点:增加了代码的复杂性,需要创建工厂类。 适用场景:当需要根据不同条件创建不同对象时,或者需要隐藏对象创建…...
el-table合计行合并
效果如下 因为合计el-table的合并方法是不生效的,所以需要修改css下手 watch: {// 应急物资的合计合并planData: {immediate: true,handler() {setTimeout(() > {const tds document.querySelectorAll(".pro_table .el-table__footer-wrapper tr>td");tds[0]…...

新手如何快速上手HTTP爬虫IP?
对于刚接触HTTP爬虫IP的新手来说,可能会感到有些困惑。但是,实际上HTTP爬虫IP并不复杂,只要掌握了基本的操作步骤,就可以轻松使用。本文将为新手们提供一个快速上手HTTP爬虫IP的入门指南,帮助您迅速了解HTTP爬虫IP的基…...
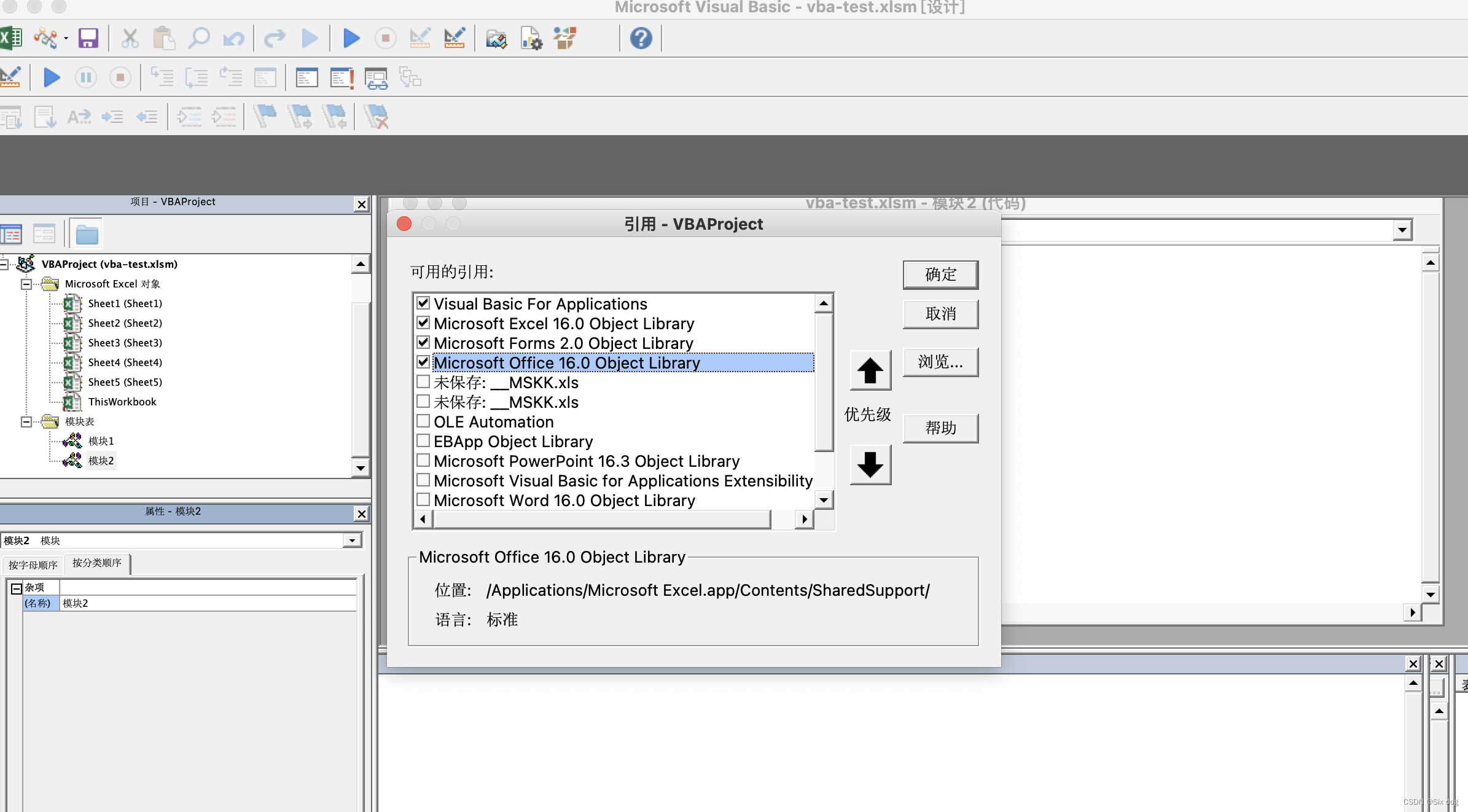
(十五)VBA常用基础知识:正则表达式的使用
vba正则表达式的说明 项目说明Pattern在这里写正则表达式,例:[\d]{2,4}IgnoreCase大小写区分,默认false:区分;true:不区分Globaltrue:全体检索;false:最小匹配Test类似p…...

vue配置@路径
第一步:安装path,如果node_module文件夹中有path就不用安装了 安装命令:npm install path --save 第二步:在vue.config.js文件(如果没有就新建)中配置 const path require("path"); function …...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
